一种机械设备状态预警方法与流程

1.本专利涉及机械设备状态监测与故障诊断领域，具体涉及一种机械设备状态 预警方法。


背景技术：

2.现代工业中机械设备扮演着重要的角色，近年来随着工业互联网技术的推 进，人们对机械设备的状态监测提出了越来越高的要求，在机械设备发生故障 的早期发现异常，开展预知性维修，对企业降低生产成本、保障生产安全具有 重要作用。然而实际生产中仍采用固定门限的报警方式，该种方法发生报警时 往往故障已经恶化到一定程度，对安全生产带来极大的威胁，需开发一种有效 的状态预警方法。基于固定门限报警方法缺陷的根源在于无法感知数据的数据 变化趋势，数据的变化趋势发生改变往往是故障发生的早期信号，因此准确捕 捉数据变化趋势的改变是机械设备预警方法的关键。
3.lstm是一种特殊设计的循环神经网络(recurrent neural networks，rnn)， 解决了传统rnn长期依赖的问题，对时序数据预测方面有着很好的表现，目前 已在语言理解、交通运输等行业得到应用。基于此，本发明提供一种基于lstm 的机械设备状态预警方法，利用lstm对机械设备正常状态数据建立预测模型并 自学习报警阈值，当预测数据与真实数据间的差异超出自学习阈值则进行报警。


技术实现要素：

4.本专利的目的是解决固定门限报警方法无法准确预警的问题，本发明提供了 一种基于lstm的机械设备状态预警方法，该方法以机械设备的振动信号为监测 数据，利用正常状态数据建立基于lstm的数据预测模型并自学习报警阈值，当 应用于预警时，分别获取预测模型的预测值与实际采集的真实值，通过马氏距 离计算预测值与真实值间的差异值，当差异值超过自学习报警阈值则进行报警。
5.一种机械设备状态预警方法，包括五个步骤：
6.步骤一：特征提取，获取机械设备正常状态数据，对正常状态数据进行特征 提取，形成机械设备正常状态特征数据集；
7.步骤二：数据划分，将正常状态特征数据集划分为xm与x
t
，分别用于模型 构建和阈值自学习；
8.步骤三：模型训练，建立lstm网络结构，利用xm训练lstm，将训练完成 的lstm模型作为预测模型；
9.步骤四：阈值自学习，以x
t
作为预测模型的测试数据，计算每组测试数据 的预测值与真实值间的马氏距离，并通过箱型图方法计算报警阈值t；
10.步骤五：状态预警，对机械设备实时振动数据进行特征提取作为实时真实值， 并基于过去一段时间的数据得到实时预测值，计算实时真实值与实时预测值的 差异并与t比较，当差异值大于t则报警，否者不报警。
11.所述的步骤一：特征提取，具体包括：采集待检测机械设备一段时间内的正 常状态振动数据，按照一定的间隔将正常状态数据划分为n组数据 z'＝{z'
,(q)
}
q＝1,...,n
，其中z'
,(q)
为第q组数据，z'内各组样本按时间顺序由小到大排列， 对每组正常状态数据进行特征提取得到特征向量集。
12.所述的步骤二：数据划分，具体包括：(1)基于lstm的预测模型通过一段 历史数据预测当前时刻的数据，将每次预测需要的历史数据的长度记为l,一般 而言l∈[30,90]，(2)预测模型的输入为长度为l的历史数据，输出为当前时刻 的预测值，(3)对正常状态特征向量集z进行划分形成预测模型的样本集。
[0013]
所述的样本集，划分方法如下：z中共包含n个时刻的特征向量，从第l个 特征向量z
(l)
开始，将l个特征向量以前和后一个特征向量分别作为样本集的输 入数据和对应的真实值，将样本集的样本组成表示为d＝{(x
(r)
,y
(r)
)}
r＝1,
…
,n-l
，x
(r)
,y
(r)
分别为样本集中第r个样本的数据和对应的真实值
[0014][0015][0016]
将样本集d划分为和两部分，其中dm用于训练预警模型，d
t
用于自学习报警阈值。
[0017]
所述的步骤三：模型训练，包含lstm网络结构确定和预测模型训练两部分， lstm网络结构需确定的参数有输入数据尺寸、输出数据尺寸、lstm隐含层神经 元个数以及lstm单元个数；lstm模型的结构确定后，采用dm对lstm模型进 行训练，令lstm模型输出的预测值为h(x)，采用均方误差作为目标函数，目标 函数的定义如式3
[0018][0019]
式中，v为每批次训练时样本的数目，x
(p)
、y
(p)
分别为每批次训练样本中第 p个样本的数据和对应的真实值。
[0020]
所述的预测模型训练，采用批量训练方法最小化o完成lstm模型的训练， 训练完成的lstm模型可作为待监测机械设备正常状态数据的预测模型。
[0021]
所述的输入数据尺寸为每次预测需要的历史数据长度l和特征维度s；输出 数据尺寸为每次预测时对s个特征的预测值；lstm隐含层神经元个数、lstm单 元个数结合实际数据确定。
[0022]
所述的步骤四：阈值自学习，具体包括：将d
t
内n-l-p个样本的数据 输入预测模型得到预测值计算预测值与真实值 的差异值，通过马氏距离计算预测值与真实值间的差异值，差 异值的计算方法如式4：
[0023]
[0024]
式中，σ为的协方差矩阵，上标t、-1分别表示转置运算和矩阵求逆；
[0025]
计算d
t
内n-l-p个样本的差异值d＝{d(i)}
i＝n-l-p
，将d由小打到大进行排列，将处 于25％的数值记为q1，处于前75％的数值记为q1，依据箱型图异常值检测方法， 自学习阈值的定义如式5所示
[0026]
t＝q3+1.5
×
(q
3-q1)
ꢀꢀ
(5)。
[0027]
所述的步骤五：状态预警，具体包括：
[0028]
获取待监测机械设备时刻t-l至t的状态数据，并提取步骤一相同的s个特征 得到特征向量z＝{z
(t-l)
,z
(t-l+1)
,
…
,z
(t)
}，以
[0029][0030]
作为预测模型的输入，将预测模型的输出记为h[x
(t)
]；依据式7计算时刻t的预 测值与真实值的差异值，当d
(t)
＞t则报警，反之不报警
[0031]
附图说明
[0032]
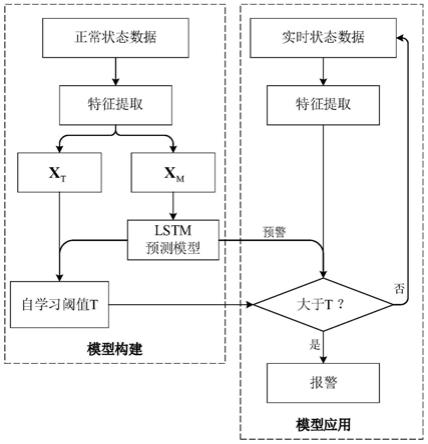
图1是本发明一种基于lstm的机械设备状态预警方法的流程图；
[0033]
图2是本发明实施例中正常状态数据的一段振动波形数据；
[0034]
图3是本发明实施例中正常状态数据的特征提取结果；
[0035]
图4是本发明实施例中预测值与真实值的对比图；
[0036]
图5是本发明实施例中测试数据各特征的变化曲线；
[0037]
图6是本发明实施例中对测试数据的实验结果。
具体实施方式
[0038]
本发明提供的一种基于lstm的机械设备状态预警方法分为模型构建和模型 应用两阶段，如附图1所示，共包括以下五个步骤：
[0039]
步骤一：特征提取。获取机械设备正常状态数据，对正常状态数据进行特征 提取，形成机械设备正常状态特征数据集。
[0040]
步骤二：数据划分。将正常状态特征数据集划分为xm与x
t
，分别用于模型 构建和阈值自学习。
[0041]
步骤三：模型训练。建立lstm网络结构，利用xm训练lstm，将训练完成 的lstm模型作为预测模型。
[0042]
步骤四：阈值自学习。以x
t
作为预测模型的测试数据，计算每组测试数据 的预测值与真实值间的马氏距离，并通过箱型图方法计算报警阈值t。
[0043]
步骤五：状态预警。对机械设备实时振动数据进行特征提取作为实时真实值， 并基于过去一段时间的数据得到实时预测值，计算实时真实值与实时预测值的 差异并与t比较，当差异值大于t则报警，否者不报警。
[0044]
以下将对本发明的五个步骤进行详细描述。
[0045]
(1)步骤一：特征提取
[0046]
采集待检测机械设备一段时间内的正常状态振动数据，按照一定的间隔将正 常状态数据划分为n组数据z'＝{z'
,(q)
}
q＝1,
…
,n
，其中z'
,(q)
为第q组数据，z'内各组样 本按时间顺序由小到大排列。对每组正常状态数据进行特征提取得到特征向量 集，例如对z'
,(q)
提取s个特征得到的特征向量为其中为 z'
,(q)
第j个特征的特征值，则由z'得到的正常状态特征向量集为z＝{z
(q)
}
q＝1,
…
,n
。
[0047]
(2)步骤二：数据划分
[0048]
基于lstm的预测模型通过一段历史数据预测当前时刻的数据，将每次预测 需要的历史数据的长度记为l,一般而言l∈[30,90]，因此预测模型的输入为长度 为l的历史数据，输出为当前时刻的预测值。为完成预测模型的训练，需对正 常状态特征向量集z进行划分形成预测模型的样本集，样本集的划分方法如下：
[0049]
z中共包含n个时刻的特征向量，从第l个特征向量z
(l)
开始，将前l个特 征向量(含第l个特征向量)和后一个特征向量分别作为样本集的输入数据和 对应的真实值，如式1、2所示。由此可将样本集的样本组成表示为 d＝{(x
(r)
,y
(r)
)}
r＝1,
…
,n-l
，x
(r)
,y
(r)
分别为样本集中第r个样本的数据和对应的真实值。
[0050][0051][0052]
在本发明预警模型的构建方法中，需要正常状态数据分别用于预测模型的训 练和报警阈值的自学习，将样本集d划分为和 两部分，其中dm用于训练预警模型，d
t
用于自学习报警阈 值。
[0053]
(3)步骤三：模型训练
[0054]
步骤三包含lstm网络的结构确定和预测模型的训练两部分。其中lstm网络 结构需确定的参数有输入数据尺寸、输出数据尺寸、lstm隐含层神经元个数以 及lstm单元个数，在本发明方法中，输入数据尺寸的具体意义为每次预测需要 的历史数据长度l和特征维度s；输出数据尺寸的具体意义为每次预测时对s个 特征的预测值；lstm隐含层神经元个数、lstm单元个数与实际数据的特点有关， 两者的个数越多模型的拟合能力越强，但也增加了模型的训练时间和过拟合的 可能性，因此需结合实际数据进行确定。
[0055]
lstm模型的结构确定后，采用dm对lstm模型进行训练，令lstm模型输出 的预测值为h(x)，采用均方误差作为目标函数，目标函数的定义如式3，采用批 量训练方法最小化o完成lstm模型的训练，训练完成的lstm模型可作为待监测 机械设备正常状态数据的预测模型。
[0056]
[0057]
式中，v为每批次训练时样本的数目，x
(p)
、y
(p)
分别为每批次训练样本中第 p个样本的数据和对应的真实值。
[0058]
(4)步骤四：阈值自学习
[0059]
预测模型具备根据一段历史数据预测当前时刻真实值的能力，当预测模型的 预测值与真实值偏离过大，表明机械设备的运行状态发生变化需要进行报警， 但预测值与真实值偏离多大时报警是预警模型是否能够准确预警的关键。为克 服人工指定报警阈值存在的缺陷，本发明通过正常状态数据和统计学方法自学 习报警预警。将d
t
内n-l-p个样本的数据输入预测模型得到预测值 计算预测值与真实值的差异值。由于每个真实值包含 多个特征且各特征间尺度不一致，因此通过马氏距离计算预测值与真实值间的 差异值，以为例，差异值的计算方法如式4。
[0060][0061]
式中，σ为的协方差矩阵，上标t、-1分别表示转置运算和矩阵求逆。
[0062]
计算d
t
内n-l-p个样本的差异值d＝{d(i)}
i＝n-l-p
，将d由小打到大进行排列，将处 于25％(下四分位数)的数值记为q1，处于前75％(下四分位数)的数值记为q1， 依据箱型图异常值检测方法，自学习阈值的定义如式5所示。
[0063]
t＝q3+1.5
×
(q
3-q1)
ꢀꢀ
(5)
[0064]
(5)步骤五：状态预警
[0065]
获取待监测机械设备时刻t-l至t的状态数据，并提取步骤一相同的s个特征 得到特征向量z＝{z
(t-l)
,z
(t-l+1)
,
…
,z
(t)
}，以
[0066][0067]
作为预测模型的输入，将预测模型的输出记为h[x
(t)
]。依据式7计算时刻t的预 测值与真实值的差异值，当d
(t)
＞t则报警，反之不报警。
[0068][0069]
为了更具体地描述本发明，以下将以某核电站主泵的泵轴振动数据为例，结 合附图对本发明一种基于lstm的机械设备状态预警方法的实施方式进行详细的 说明。
[0070]
(1)步骤一：特征提取
[0071]
如附图2所示为某核电主泵泵轴正常状态下1秒的振动波形图，对该台主泵 正常状态下泵轴160分钟的振动波形数据进行特征提取，依次提取峰峰值、半 倍频、一倍频幅值、二倍频幅值、三倍频幅值、四倍频幅值和五倍频幅值，共 得到9600组特征向量，即本发明内容中n＝9600，s＝7。各特征随时间的变化曲 线如附图3所示，feature_1～feature_7分别为峰峰值、半倍频、一倍频幅值、 二倍频幅值、三倍频幅值、四倍频幅值和五倍频幅值，图中每个时间点对应的7 个特征值组成一组特征向量。
[0072]
(2)步骤二：数据划分
[0073]
本实施例中，每次预测需要的历史数据的长度l＝60，因此样本集中任一样 本的输入数据和对应的真实值分别如式8、9所示，其中9540≥r≥1。
[0074][0075][0076]
式8、9中，分别为特征向量集中第r组特征向量的峰峰 值、半倍频、一倍频幅值、二倍频幅值、三倍频幅值、四倍频幅值和五倍频幅 值。
[0077]
由此可得到样本数为9540的样本集d＝{(x
(r)
,y
(r)
)}
r＝1,
…
,9540
，将d按1:1的比例 划分为和两部分，其中dm用于训练预警 模型，d
t
用于自学习报警阈值。
[0078]
(3)步骤三：模型训练
[0079]
输入数据尺寸与单次预测所需要的历史数据长度、特征维度有关，因此在本 实施例中输入数据尺寸为60
×
7；输出数据尺寸与特征维度有关，在本实施例中 为7；此外，在本实施例中lstm单元个数为2，隐含层神经元个数均为128，该 数据为经实验得到的优化值。
[0080]
采用dm对lstm模型进行训练，令lstm模型输出的预测值为h(x)，采用均 方误差作为目标函数，目标函数的定义如式10，采用批量训练方法最小化o完 成lstm模型的训练，每批次训练的样本数目为1024，共训练2000轮，训练完 成的lstm模型可作为待监测机械设备正常状态数据的预测模型，如附图4为预 测模型的预测值(虚线)与真实值(实线)的对比图。
[0081][0082]
式中，x
(p)
、y
(p)
∈dm分别为每批次训练样本中第p个样本的数据和对应的真 实值。
[0083]
(4)步骤四：阈值自学习
[0084]dm
中的协方差矩阵如式11所示，依据发明内容中式4可求得下四分位 数q1＝2.901,上四分位数q3＝4.251，则报警预阈值t＝4.251+1.5
×
(4.251-2.901)＝6.276。
[0085][0086]
(5)步骤五：状态预警
[0087]
附图5为用于验证本发明效果的测试数据的7个特征随时间的变化曲线，图 中用椭圆标注出了特征的变化规律发生变化的时间，由图可看出峰峰值、半倍 频幅值、一倍频
幅值、二倍频幅值在2000时间点后慢慢增大。
[0088]
依次滑动截取测试数据60个时间点的特征向量作为预测模型的输入计算得 到下一时刻的预测值，依据发明内容中式7计算预测值与真实值的差异值。