一种电气装备制造生产过程协同管理平台

1.本发明涉及一种电气装备制造生产过程协同管理平台，属于智能制造技术领域。


背景技术：

2.目前，装备制造业主要是采用传统的生产经营方式，制造企业制定生产计划并且向上游供货商采购生产所需的原材料，在原材料送达之后，生产车间开始逐个完成产品的生产、装配等任务。这种方式下，每件产品从制定计划开始，主要存在原材料的运输时间、生产车间调配生产所需的机床、量具、刀具、夹具的时间、实际生产时间及最终产品的装配时间。但是，装配制造所需的生产资源分布比较分散，原材料实际送达时间不统一，而实际生产多数情况下需要在所有原材料都送达后才开始生产任务，这样会存在较长的等待时间，同时也增加了生产计划的不确定性。另外，不同时间送达的原材料也需要先存放起来，潜在的增加了仓储成本。工厂车间按序逐个生产产品，需要频繁切换生产线路，工厂车间的生产效率会大受影响。此外，不同型号的机床、刀具、夹具等资源的使用成本也存在着差异。因此，合理地制定整个生产计划同时对资源进行优化配置显得异常重要。


技术实现要素：

3.本发明的目的公开一种电气装备制造生产过程协同管理平台，基于最小粒度划分将待生产的产品拆分成不同的构件，然后利用成组技术，将同种构件组合在一起组成新的任务，不同构件归为不同任务，以实现平台的任务分解与重组；为各项任务分配生产资源，构建总时间、总成本最小化的多目标优化模型，通过遗传算法求解最优解或次优解，以实现平台的资源优化配置。本发明平台能解决协同制造环境下资源选择优化的难题，提供多资源优化配置解决方案。
4.鉴于装备制造生产中存在着生产资源分布分散，资源利用率低，缺少服务平台，资源共享不畅，资源标准规范不统一，企业管理模式落后等一系列问题，本发明提出基于改进遗传算法的电气装备制造资源优化配置方法，针对不同产品制造需求，制定个性化的组装方案，上游供应商根据实时动态信息，及时提供配套供应。本发明还提出基于改进遗传算法构建装备制造总时间、总成本最小化的多目标优化模型，以实现装备制造过程中生产资源的最优化配置，提升产品的生产效率。
5.本发明技术方案：
6.一种电气装备制造生产过程协同管理平台，其特征是，包括企业生产计划模块、任务分解与重组模块、资源优化配置模块；还包括产品属性信息库、生产资料信息库，生产任务清单数据库；其中：
7.所述企业生产计划模块为生产企业制定的年度生产计划；
8.所述生产资料信息库用于记录和更新采购及库存信息，包括采集入库产品信息和和生产消耗存量信息；
9.所述任务分解与重组模块基于最小粒度划分将生产任务清单数据库中待生产的
产品依据产品属性信息库拆分成不同的构件，然后利用重组技术，将同种构件组合在一起组成新的任务更新生产任务清单数据库，不同构件归为不同任务；具体的，所述任务分解与重组模块从生产任务清单数据库获取生产计划，从企业的产品属性信息库导出要进行的生产产品属性信息；进一步的，将生产任务拆分成粒度最小的构件；对最小构件进行组合，将同一构件重新归为同一子任务，不同构件组合为不同的子任务；根据组合结果，生成新的工厂车间生产任务清单并保存至生产过程协同管理平台的生产任务清单数据库。
10.所述资源优化配置模块，包括信息获取子模块、信息编码子模块、计算子模块、优化子模块。为生产任务清单数据库中各项任务分配生产资源，构建总时间、总成本最小化的多目标优化模型，通过遗传算法求解最优解或次优解。处理步骤：首先初始化解空间，交叉变异得到子代种群，将父代种群和新产生的子代种群合，计算当前种群中个体的patora等级及排序，计算拥挤度，与设定阈值比较从而淘汰不适应当前种群环境的解，当出现进化十代而没有比较明显的提升时，说明算法已经收敛到一个稳定的解，此时可以输出计算得到的资源配置方案。
11.具体的：
12.所述信息获取子模块包括：从生产过程协同管理平台的生产任务清单数据库中获取重组之后的生产任务清单；
13.从生产过程协同管理平台的产品属性信息库中获取所有生产车间的机床属性信息、刀具属性信息、夹具属性信息、量具属性信息，包括使用成本、功率、所在车间等，这些是为资源优化配置模块计算时间、成本等提供相关的数据；
14.从生产过程协同管理平台的生产资料信息库中获取目前各种生产资源的数目、使用情况、生产状态等信息；
15.所述计算子模块包括：
16.1)计算单件产品的生产时间：
17.根据企业生产计划模块确定生产n种产品，通过分解与重组模块得到
18.m种通用构件及n种特定构件；那么，
19.产品k,k∈(1,n)的生产时间为：
[0020][0021]
其中，代表产品k的构件i最长的可能生产时间(这里主要考虑到任务重组之后，通用构件会集中生产，但是实际生产时还是会存在一个生产的先后顺序问题，我们这里取一个最大时间作为所有产品该构件的生产时间)，代表构件i生产过程中需要的资源调配时间，代表构件i生产过程中需要的装配时间；
[0022]
2)计算所有产品总的生产时间t
[0023][0024]
3)计算单件产品的生产成本
[0025]
产品k,k∈(1,n)的生产成本为：
[0026][0027]
其中，代表构件i生产过程中需要的制造成本，代表构件i生产过程中需要的资源调配成本，代表构件i生产过程中需要的装配成本；
[0028]
4)计算所有产品总的生产成本c
[0029][0030]
所述编码子模块用于对需要优化配置的生产资源进行信息编码:
[0031]
为了方便进行遗传算法的搜索，需要将待优化的资源信息编码成为染色体的基因信息；本发明采用实数编码和二进制编码；实数编码能够表示的更大范围的数据，适合复杂场景下的寻优问题，所以本发明选用一个多层的实数编码进行染色体信息编码；
[0032]
染色体中将存放构件信息、机床信息、刀具信息、夹具信息、量具信息，整体长度为2∑
i k
i
j
i
c
i
g
i
q
i
,其中，k
i
代表产品k的i构件,j
i
代表构件i分配的机床，c
i
代表构件i分配到的刀具，g
i
代表构件i分配到的夹具，q
i
代表构件i分配到的量具；
[0033]
所述优化子模块用于：
[0034]
1)构建多目标最小化的优化函数
[0035]
为了使总生产时间、总生产成本最小化，构建多目标优化函数：
[0036]
f＝min(t,c)
ꢀꢀꢀ
(5)
[0037]
2)初始化解空间
[0038]
遗传算法的初代解可以通过随机生成的p个染色体串来代表，其中每个染色体代表一个个体，所有染色体构成了一个初代种群，并以此为进化的起点开始最优解的求解；
[0039]
3)交叉变异
[0040]
随机选择两个当前种群中的个体，在其染色体的前∑
i k
i
j
i
c
i
g
i
q
i
位随机选择交叉位置进行交叉操作；随机选择变异个体，选择变异位置a和位置b，最后把个体位置a和位置b对应的编码信息调换，得到变异个体；
[0041]
4)父代子代种群合并
[0042]
这里采用精英策略，将交叉、变异生成的子代种群和父代种群同时保留下来，为了将父代中优良个体保存下来；
[0043]
5)快速非支配排序
[0044]
包括pareto支配关系定义：在处理多目标最小化优化问题时，有m个目标分量f
i
(x),i＝1...m,这里是t和c,任意给定两个决策变量x
a
，x
b
，如果有以下两个条件成立，则称x
a
支配x
b
；
[0045]
a.对于都有f
i
(x
a
)≤f
i
(x
b
)成立
[0046]
b.使得f
i
(x
a
)<f
i
(x
b
)成立
[0047]
如果一个决策变量，不存在其他决策变量能够支配它，那么就称决策变量为非支配解；
[0048]
包括pareto等级定义：
[0049]
在一组解中，非支配解pareto定义为1，将非支配解从解的集合中删除，剩下解的pareto等级定义为2，依次类推，可以得到该解集合中所有解的pareto等级；
[0050]
包括快速非支配排序：
[0051]
a.对解空间中的每个个体p，计算被支配数及支配解；
[0052]
b.将被支配数为0的个体分入pateto等级1的集合f1；
[0053]
c.将集合f1中所有个体的除当前个体外，被支配数为0的支配解分到集合f2；
[0054]
d.重复步骤c,将当前种群所有个体进行等级划分；
[0055]
6)计算拥挤度
[0056]
为了使计算得到的解能够均匀分布在的我们的目标解空间中，我们引入一个拥挤度的指标n
d
：
[0057]
a.初始时，n
d
＝0；
[0058]
b.循环遍历每个目标函数f
m
，这里是t和c:
[0059]
为个体目标函数值f
m
的最大值，为个体目标函数值f
m
的最小值，然后对该等级的个体进行排序，将排序之后的两个边界的拥挤度t
d
和h
d
置为∞，最后计算
[0060][0061]
其中，f
m
(p+1)是该个体p排序后后一位的目标函数值；
[0062]
7)选择
[0063]
对经过快速非支配排序及拥挤度计算后的解空间中的个体，根据期望值sota(最初可以按照之前生产方式下计算总时间、总成本),将当前种群中的解能够达到期望值sota的80％效果以上的保留，其余删除，得到选择操作之后的新的解空间；
[0064]
8)计算当前解空间中最优分配方案
[0065]
计算所述解空间中的所有分配方案，将最优分配方案保存，并更新期望值sota；
[0066]
9)进化终止条件
[0067]
通过比较最近10代得到的分配方案的结果，如果效果提升小于0.1％，说明算法已经收敛，可以将目前结果作为最优解或次优解输出资源分配方案；否则，继续执行交叉变异。
[0068]
本发明的有益效果是：
[0069]
本发明平台具有较强的可行性，对实际生产中资源配置能够从全局角度出发给出一个最优解，为装备制造业高效率生成提供了可行的解决方案。
附图说明
[0070]
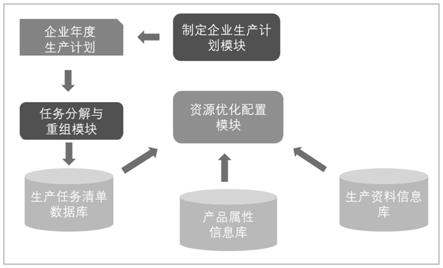
图1生产过程协同管理平台的构成及各模块连接关系图
[0071]
图2资源优化配置模块的构成和功能关系图
[0072]
图3本发明平台总流程图
[0073]
图4制造任务分解与重组
[0074]
图5本发明改进遗传算法搜索资源配置方案工作流程图
具体实施方式
[0075]
下面通过实施例结合附图进一步说明本发明。
[0076]
如图1所示：
[0077]
一种电气装备制造生产过程协同管理平台，其特征是，包括企业生产计划模块、任务分解与重组模块、资源优化配置模块；还包括产品属性信息库、生产资料信息库，生产任务清单数据库；其中：
[0078]
所述企业生产计划模块为生产企业制定的年度生产计划；
[0079]
所述生产资料信息库用于记录和更新采购及库存信息，包括采集入库产品信息和和生产消耗存量信息；
[0080]
所述任务分解与重组模块基于最小粒度划分将生产任务清单数据库中待生产的产品依据产品属性信息库拆分成不同的构件，然后利用重组技术，将同种构件组合在一起组成新的任务更新生产任务清单数据库，不同构件归为不同任务；具体的，所述任务分解与重组模块从生产任务清单数据库获取生产计划，从企业的产品属性信息库导出要进行的生产产品属性信息；进一步的，将生产任务拆分成粒度最小的构件；对最小构件进行组合，将同一构件重新归为同一子任务，不同构件组合为不同的子任务；根据组合结果，生成新的工厂车间生产任务清单并保存至生产过程协同管理平台的生产任务清单数据库。
[0081]
如图2所示：
[0082]
所述资源优化配置模块，包括信息获取子模块、信息编码子模块、计算子模块、优化子模块：为生产任务清单数据库中各项任务分配生产资源，构建总时间、总成本最小化的多目标优化模型，通过遗传算法求解最优解或次优解。
[0083]
首先初始化解空间，交叉变异得到子代种群，将父代种群和新产生的子代种群合，计算当前种群中个体的patora等级及排序，计算拥挤度，与设定阈值比较从而淘汰不适应当前种群环境的解，当出现进化十代而没有比较明显的提升时，说明算法已经收敛到一个稳定的解，此时可以输出计算得到的资源配置方案。
[0084]
具体的
[0085]
所述信息获取子模块包括：从生产过程协同管理平台的生产任务清单数据库中获取重组之后的生产任务清单；
[0086]
从生产过程协同管理平台的产品属性信息库中获取所有生产车间的机床属性信息、刀具属性信息、夹具属性信息、量具属性信息，包括使用成本、功率、所在车间等，这些是为资源优化配置模块计算时间、成本等提供相关的数据；
[0087]
从生产过程协同管理平台的生产资料信息库中获取目前各种生产资源的数目、使用情况、生产状态等信息；
[0088]
所述计算子模块包括：
[0089]
1)计算单件产品的生产时间：
[0090]
根据企业生产计划模块确定生产n种产品，通过分解与重组模块得到
[0091]
m种通用构件及n种特定构件；那么，
[0092]
产品k,k∈(1,n)的生产时间为：
[0093]
[0094]
其中，代表产品k的构件i最长的可能生产时间(这里主要考虑到任务重组之后，通用构件会集中生产，但是实际生产时还是会存在一个生产的先后顺序问题，我们这里取一个最大时间作为所有产品该构件的生产时间)，代表构件i生产过程中需要的资源调配时间，代表构件i生产过程中需要的装配时间；
[0095]
2)计算所有产品总的生产时间t
[0096][0097]
3)计算单件产品的生产成本
[0098]
产品k,k∈(1,n)的生产成本为：
[0099][0100]
其中，代表构件i生产过程中需要的制造成本，代表构件i生产过程中需要的资源调配成本，代表构件i生产过程中需要的装配成本；
[0101]
4)计算所有产品总的生产成本c
[0102][0103]
所述编码子模块用于对需要优化配置的生产资源进行信息编码:
[0104]
为了方便进行遗传算法的搜索，需要将待优化的资源信息编码成为染色体的基因信息；本发明采用实数编码和二进制编码；实数编码能够表示的更大范围的数据，适合复杂场景下的寻优问题，所以本发明选用一个多层的实数编码进行染色体信息编码；
[0105]
染色体中将存放构件信息、机床信息、刀具信息、夹具信息、量具信息，整体长度为2∑
i k
i
j
i
c
i
g
i
q
i
,其中，k
i
代表产品k的i构件,j
i
代表构件i分配的机床，c
i
代表构件i分配到的刀具，g
i
代表构件i分配到的夹具，q
i
代表构件i分配到的量具；
[0106]
所述优化子模块用于：
[0107]
1)构建多目标最小化的优化函数
[0108]
为了使总生产时间、总生产成本最小化，构建多目标优化函数：
[0109]
f＝min(t,c)
ꢀꢀꢀ
(10)
[0110]
2)初始化解空间
[0111]
遗传算法的初代解可以通过随机生成的p个染色体串来代表，其中每个染色体代表一个个体，所有染色体构成了一个初代种群，并以此为进化的起点开始最优解的求解；
[0112]
3)交叉变异
[0113]
随机选择两个当前种群中的个体，在其染色体的前∑
i k
i
j
i
c
i
g
i
q
i
位随机选择交叉位置进行交叉操作；随机选择变异个体，选择变异位置a和位置b，最后把个体位置a和位置b对应的编码信息调换，得到变异个体；
[0114]
4)父代子代种群合并
[0115]
这里采用精英策略，将交叉、变异生成的子代种群和父代种群同时保留下来，为了
将父代中优良个体保存下来；
[0116]
5)快速非支配排序
[0117]
包括pareto支配关系定义：在处理多目标最小化优化问题时，有m个目标分量f
i
(x),i＝1...m,这里是t和c,任意给定两个决策变量x
a
，x
b
，如果有以下两个条件成立，则称x
a
支配x
b
；
[0118]
a.对于都有f
i
(x
a
)≤f
i
(x
b
)成立
[0119]
b.使得f
i
(x
a
)<f
i
(x
b
)成立
[0120]
如果一个决策变量，不存在其他决策变量能够支配它，那么就称决策变量为非支配解；
[0121]
包括pareto等级定义：
[0122]
在一组解中，非支配解pareto定义为1，将非支配解从解的集合中删除，剩下解的pareto等级定义为2，依次类推，可以得到该解集合中所有解的pareto等级；
[0123]
包括快速非支配排序：
[0124]
a.对解空间中的每个个体p，计算被支配数及支配解；
[0125]
b.将被支配数为0的个体分入pateto等级1的集合f1；
[0126]
c.将集合f1中所有个体的除当前个体外，被支配数为0的支配解分到集合f2；
[0127]
d.重复步骤c,将当前种群所有个体进行等级划分；
[0128]
6)计算拥挤度
[0129]
为了使计算得到的解能够均匀分布在的我们的目标解空间中，我们
[0130]
引入一个拥挤度的指标n
d
：
[0131]
a.初始时，n
d
＝0；
[0132]
b.循环遍历每个目标函数f
m
，这里是t和c:
[0133]
为个体目标函数值f
m
的最大值，为个体目标函数值f
m
的最小值，然后对该等级的个体进行排序，将排序之后的两个边界的拥挤度t
d
和h
d
置为∞，最后计算
[0134][0135]
其中，f
m
(p+1)是该个体p排序后后一位的目标函数值；
[0136]
7)选择
[0137]
对经过快速非支配排序及拥挤度计算后的解空间中的个体，根据期望值sota(最初可以按照之前生产方式下计算总时间、总成本),将当前种群中的解能够达到期望值sota的80％效果以上的保留，其余删除，得到选择操作之后的新的解空间；
[0138]
8)计算当前解空间中最优分配方案
[0139]
计算所述解空间中的所有分配方案，将最优分配方案保存，并更新期望值sota；
[0140]
9)进化终止条件
[0141]
通过比较最近10代得到的分配方案的结果，如果效果提升小于0.1％，说明算法已经收敛，可以将目前结果作为最优解或次优解输出资源分配方案；否则，继续执行交叉变异。
[0142]
基于上述技术方案，进一步本发明平台的总工作流程图(如图3所示),方法过程包括：
[0143]
步骤1，任务分解与重组：
[0144]
基于最小粒度划分将待生产的产品拆分成不同的构件，然后利用成组技术，将同种构件组合在一起组成新的任务，不同构件归为不同任务。
[0145]
步骤2，资源优化配置：
[0146]
为各项任务分配生产资源，构建总时间、总成本最小化的多目标优化模型，通过遗传算法求解最优解或次优解。
[0147]
图4是根据当前任务进行的任务划分与重组，对同种构件集中生产，减少中间线路切换所浪费的时间，以达到全局最优。
[0148]
具体实施过程如下：
[0149]
1.1获取生产计划，从企业中已有的生产过程协同管理平台导出要进行的生产产品属性信息；
[0150]
1.2根据1.1中获取的产品的属性信息，将生产任务拆分成粒度最小的构件；
[0151]
1.3对1.2步骤拆分之后的构件进行组合，将同一构件重新归为同一子任务，不同构件归为不同的子任务；
[0152]
1.4根据1.3步骤组合结果，生成新的工厂车间生产任务清单并保存至生产过程协同管理平台。
[0153]
步骤2，资源优化配置。
[0154]
图5是基于遗传算法所进行的资源优化配置的详细步骤。首先初始化解空间，交叉变异得到子代种群，将父代种群和新产生的子代种群合，计算当前种群中个体的patora等级及排序，计算拥挤度，与设定阈值比较从而淘汰不适应当前种群环境的解，当出现进化十代而没有比较明显的提升时，说明算法已经收敛到一个稳定的解，此时可以输出计算得到的资源配置方案。
[0155]
具体实施过程如下：
[0156]
2.1从生产过程协同管理平台获取重组之后的生产任务清单；
[0157]
2.2从生产过程协同管理平台获取所有生产车间的机床属性信息、刀具属性信息、夹具属性信息、量具属性信息，包括使用成本、功率、所在车间等，这些是为后续步骤计算时间、成本等提供相关的数据；
[0158]
2.3从生产过程协同管理平台获取目前各种生产资源的数目、使用情况、生产状态等信息；
[0159]
2.4计算单件产品的生产时间：
[0160]
假设企业计划生产n种产品，通过模块分解与重组得到m种通用构件及n种特定构件。那么，
[0161]
产品k,k∈(1,n)的生产时间为：
[0162][0163]
其中，代表产品k的构件i最长的可能生产时间(这里主要考虑到任务重组之后，通用构件会集中生产，但是实际生产时还是会存在一个生产的先后顺序问题，我们这里取一个最大时间作为所有产品该构件的生产时间)，代表构件i生产过程中需要的
资源调配时间，代表构件i生产过程中需要的装配时间；
[0164]
2.5计算所有产品总的生产时间t
[0165][0166]
2.6计算单件产品的生产成本
[0167]
产品k,k∈(1,n)的生产成本为：
[0168][0169]
其中，代表构件i生产过程中需要的制造成本，代表构件i生产过程中需要的资源调配成本，代表构件i生产过程中需要的装配成本。
[0170]
2.7计算所有产品总的生产成本c
[0171][0172]
2.8构建多目标最小化的优化函数
[0173]
为了使总生产时间、总生产成本最小化，我们构建多目标优化函数：
[0174]
f＝min(t,c)
ꢀꢀꢀ
(15)
[0175]
2.9对需要优化配置的生产资源进行信息编码
[0176]
为了方便进行遗传算法的搜索，需要将待优化的资源信息编码成为染色体的基因信息。目前，比较常用的是两种编码方式：实数编码和二进制编码。实数编码能够表示的更大范围的数据，适合复杂场景下的寻优问题，所以本文这里将选用一个多层的实数编码进行染色体信息编码。
[0177]
染色体中将存放构件信息、机床信息、刀具信息、夹具信息、量具信息，整体长度为2∑
i k
i
j
i
c
i
g
i
q
i
,其中，k
i
代表产品k的i构件,j
i
代表构件i分配的机床，c
i
代表构件i分配到的刀具，g
i
代表构件i分配到的夹具，q
i
代表构件i分配到的量具。
[0178]
2.10初始化解空间
[0179]
遗传算法的初代解可以通过随机生成的p个染色体串来代表，其中每个染色体代表一个个体，所有染色体构成了一个初代种群，并以此为进化的起点开始最优解的求解。
[0180]
2.11交叉变异
[0181]
随机选择两个当前种群中的个体，在其染色体的前∑
i k
i
j
i
c
i
g
i
q
i
位随机选择交叉位置进行交叉操作；随机选择变异个体，选择变异位置a和位置b，最后把个体位置a和位置b对应的编码信息调换，得到变异个体。
[0182]
2.12父代子代种群合并
[0183]
这里采用精英策略，将2.11步骤中交叉、变异生成的子代种群和父代种群同时保留下来，为了将父代中优良个体保存下来。
[0184]
2.13快速非支配排序
[0185]
2.13.1 pareto支配关系定义
[0186]
在处理多目标最小化优化问题时，有m个目标分量f
i
(x),i＝1...m,这里是t和c,
任意给定两个决策变量x
a
，x
b
，如果有以下两个条件成立，则称x
a
支配x
b
。
[0187]
a.对于都有f
i
(x
a
)≤f
i
(x
b
)成立
[0188]
b.使得f
i
(x
a
)<f
i
(x
b
)成立
[0189]
如果一个决策变量，不存在其他决策变量能够支配它，那么就称决策变量为非支配解。
[0190]
2.13.2pareto等级定义
[0191]
在一组解中，非支配解pareto定义为1，将非支配解从解的集合中删除，剩下解的pareto等级定义为2，依次类推，可以得到该解集合中所有解的pareto等级。
[0192]
2.13.3快速非支配排序
[0193]
a.对解空间中的每个个体p，计算被支配数及支配解；
[0194]
b.将被支配数为0的个体分入pateto等级1的集合f1；
[0195]
c.将集合f1中所有个体的除当前个体外，被支配数为0的支配解分到集合f2；
[0196]
d.重复步骤c,将当前种群所有个体进行等级划分。
[0197]
2.14计算拥挤度
[0198]
为了使计算得到的解能够均匀分布在的我们的目标解空间中，我们引入一个拥挤度的指标n
d
：
[0199]
a.初始时，n
d
＝0；
[0200]
b.循环遍历每个目标函数f
m
，这里是t和c:
[0201]
为个体目标函数值f
m
的最大值，为个体目标函数值f
m
的最小值，然后对该等级的个体进行排序，将排序之后的两个边界的拥挤度t
d
和h
d
置为∞，最后计算
[0202][0203]
其中，f
m
(p+1)是该个体p排序后后一位的目标函数值。
[0204]
2.15选择
[0205]
对经过步骤2.13、2.14快速非支配排序及拥挤度计算后的解空间中的个体，根据期望值sota(最初可以按照之前生产方式下计算总时间、总成本),将当前种群中的解能够达到期望值sota的80％效果以上的保留，其余删除，得到选择操作之后的新的解空间。
[0206]
2.16计算当前解空间中最优分配方案
[0207]
计算2.15中得到的解空间中的所有分配方案，将最优分配方案保存，并更新期望值sota。
[0208]
2.17进化终止条件
[0209]
通过比较最近10代得到的分配方案的结果，如果效果提升小于0.1％，说明算法已经收敛，可以将目前结果作为最优解或次优解输出资源分配方案。否则，继续执行步骤2.11。