一种非气密倒装互连凸点贮存寿命评估方法与流程

1.本发明涉及一种非气密倒装互连凸点贮存寿命评估方法，适用于非气密倒装焊封装集成电路互连凸点结构的寿命评估。


背景技术：

2.倒装焊互联封装具有互连距离短、寄生电容和寄生电感小，芯片的i/o电极设置自由度高以及封装密度高的显著优点，但由于倒装焊器件多用于大功率器件，需要热沉进行散热，多采用非气密封装。相对于气密性封装，其互连结构在长期贮存环境中的可靠性面临着更加艰巨的考验。因此，有必要对非气密倒装互连凸点的贮存寿命进行评估。
3.传统寿命评估试验方法一般采取温度、湿度或温循等应力作为加速条件，通过加速寿命试验，定期对器件参数进行测量，根据阶段性测量数据大致得到器件失效时间，进而进行数据统计分析，通过不同梯度试验条件的寿命分布模型推算经验加速因子，进而估算正常条件下的加速寿命；或采用加速退化实验，定期检测互连结构剪切强度，计算互连结构伪寿命，后结合失效机理加速模型推出正常贮存环境下封装体的贮存寿命，利用此类方法对集成电路互连结构进行贮存寿命评估具有较大误差，适应性较差。
4.定期检测封装体敏感参数，获取参数退化趋势，进行伪寿命分析，无法准确获取互连结构失效时间，具有较大误差；
5.从伪寿命分布模型中推算得平均寿命，不具备高可靠检验要求，以此平均寿命计算的正常贮存寿命存在可靠度不足；
6.采用基于伪寿命分布得到的特征寿命推算加速因子，没有考虑失效机理的关键影响性，仅通过传统的数据统计分析可靠性预计方法不具备科学性；或直接采用代入粗略估计参数的失效机理加速模型计算互连结构在正常贮存条件下的贮存寿命，适用性及准确度不足；
7.因此，此类方法不能准确地评估封装互连结构的贮存寿命。


技术实现要素：

8.本发明解决的技术问题是：克服现有技术的不足，提出一种非气密倒装互连凸点贮存寿命评估方法，该方法可更加准确、有针对性的评估非气密倒装互连凸点的贮存寿命。
9.本发明解决技术的方案是：
10.一种非气密倒装互连凸点贮存寿命评估方法，包括以下步骤:
11.(1)制备n只菊花链非气密倒装焊集成电路，记录每只电路编号，试验前测试电路通路情况及初始阻值，随机分为n/n组，n为n的整数倍，n≥5，n≥45；
12.(2)n/n组电路分别分配至温度循环试验、高温贮存试验、恒定湿热试验的三种试验条件下进行加速寿命试验，以定数截尾的试验方案开展试验，直至全部电路阻值异常，试验停止；
13.(3)定义焊点失效的标准为全动态导通电阻系统检测到瞬态阻值超过20％，记录
失效时间数据，使用失效分析方法分析失效凸点，确定失效机理，选取建立产品寿命与施加环境载荷之间关系的加速模型；
14.(4)根据步骤(2)中三种试验类型下的三级梯度试验条件的失效时间数据，对失效时间数据进行频率直方图分析，确定电路样品寿命分布类型，采用极大似然法对寿命分布函数的参数进行拟合，分别得到寿命分布类型对应的寿命分布函数，得到90％可靠度下阵列锡基焊料倒装互连微凸点非气密封装的失效寿命t
r
及平均失效时间mttf；
15.(5)在单侧置信区间不超过寿命分布函数值20％时，将不同梯度得到的失效寿命t
r
分别代入加速模型；在单侧置信区间不超过寿命分布函数值20％时，则将平均失效时间mttf分别代入加速模型，拟合计算出加速模型待估参数，结合电路样品实际贮存条件，对电路样品的实际贮存寿命进行评估。
16.进一步的，步骤(5)中，将不同梯度得到的t
r
分别代入加速模型，温度循环试验代入coffin
‑
manson模型或其修正模型norris
‑
landzberg模型，高温贮存试验代入arrhenius模型，恒定湿热试验数据代入lawson模型。
17.进一步的，步骤(3)中，以检测到10次或10次以上的不小于300ω的瞬断电阻作为失效判据，记录失效时间数据。
18.进一步的，步骤(3)中，失效分析方法包括sem、ct、tdr/eotpr。
19.进一步的，coffin
‑
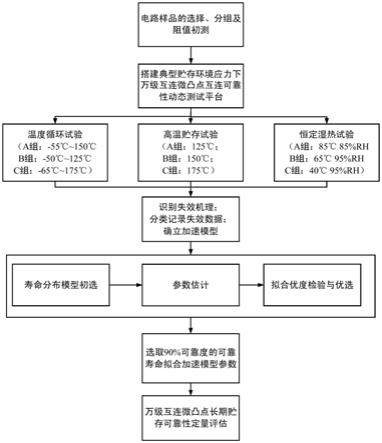
manson模型
20.其中，δt
office
为装置应用温度循环范围，δt
aoto
为加速试验温度范围，q为coffin
‑
manson指数。
21.进一步的，arrhenius模型
22.式中dm/dt为敏感参数的退化速率，a为扩散常数，ea为激活能，k为玻尔兹曼常数，t为绝对温度。
23.本发明与现有技术相比的有益效果是：
24.(1)本发明以链路通断作为失效时间的判断准则，实时准确检测互连通路的贮存可靠性，避免在伪寿命推算过程中引入误差；
25.(2)本发明定量指定可靠度量级，分析加速因子，由多组试验结果推算90％以失效分析结果确定加速模型，通过准确试验数据估算相应失效机理加速模型参数取值，更加准确，适用性更强。
附图说明
26.图1为本发明非气密倒装互连凸点贮存寿命评估方法的流程图；
27.图2为试验事件记录图；
28.图3为寿命分布图；
29.图4为加速模型多元拟合示意图。
具体实施方式
30.下面结合实施例对本发明作进一步阐述。
31.图1为本发明非气密倒装互连凸点贮存寿命评估方法的流程图。如图1所示，依据本发明实施例的非气密倒装互连凸点贮存寿命评估方法的步骤包括：
32.步骤(1)：制备45只菊花链非气密倒装焊集成电路，记录每只电路得编号，试验前测试电路通路情况及初始阻值，随机分为9组；
33.步骤(2)：9组电路分别分配至温度循环试验、高温贮存试验、恒定湿热试验的3种试验条件下进行加速寿命试验，以定数截尾的试验方案开展试验，直至全部电路阻值异常，试验停止，因此数据中没有删失数据；
34.步骤(3)：定义焊点失效的标准为全动态导通电阻系统检测到10次或10次以上的不小于300ω的瞬断电阻或者定义焊点失效的标准为全动态导通电阻系统检测到瞬态阻值超过20％，使用sem、ct、tdr/eotpr的失效分析方法分析失效凸点，确定主要失效机理，选取加速模型；
35.步骤(4)：试验结束后，利用寿命分布图示法对试验数据进行分析，确定电路样品寿命分布类型，采用极大似然法对寿命分布函数的参数进行拟合，分别得到它们的寿命分布函数；
36.步骤(5)：根据三种试验类型下的3级梯度试验条件的失效数据，分别推出相应寿命分布函数，均根据步骤(4)得到90％可靠度下面阵列锡基焊料倒装互连微凸点非气密封装的失效寿命t
r
；
37.步骤(6)：将不同梯度得到的t
r
分别代入加速模型，温度循环试验即可代入coffin
‑
manson的norris
‑
landzberg的修正模型或paris
‑
law模型，高温贮存试验可代入arrhenius模型；恒定湿热试验数据可代入lawson模型，拟合计算出加速模型待估参数，见图4；
38.步骤(7)：根据步骤(5)和步骤(6)的结果，结合电路样品实际贮存条件，对电路样品的实际贮存寿命进行评估。
39.所述步骤(1)中的电路样品，均为同一批菊花链封装产品，菊花链路便于实时监控互连通路阻值变化，反映互连通路可靠性。采用对每个器件布置多个网络进行独立的菊花链设计，这种设计能够为最先失效区域提供附加信息；此外，印制电路板上的菊花链设计在印制电路板的顶层，这样可以避免将通孔失效误判为菊花链失效。
40.所述步骤(2)中，分别采用恒定高温应力加速寿命试验、恒定湿热加速寿命试验和温度循环加速寿命试验三类加速寿命试验，对菊花链路进行评估，并采用电阻值作为敏感参数，用来评价面阵列锡基焊料倒装互连凸点的贮存寿命。
41.所述步骤(3)中，可以以检测到10次或10次以上的不小于300ω的瞬断电阻作为失效判据，或者焊点失效的标准为全动态导通电阻系统检测到瞬态阻值超过20％，精准记录失效前工作时间；
42.所述步骤(3)中，互连凸点失效后，取出进行失效分析，根据jedec jep122h
‑
2016《半导体器件的失效机理和模型》，结合载荷环境与焊点形貌确定失效机理，选定加速模型，涉及模型如下：
43.coffin
‑
manson模型
[0044][0045]
δtoffice＝装置应用温度循环范围
[0046]
δt aoto＝加速试验温度范围
[0047]
q＝coffin
‑
manson指数，一个经验导出的常数，由失效机制决定
[0048]
温度交变应力作用下的疲劳失效，焊点疲劳失效的加速试验模型可选用改进的coffin
‑
manson模型，norris
‑
landzberg对coffin
‑
manson方法的修改增加了与焊点疲劳相关的附加乘法项。这些附加项因子是作为幂律的循环频率因子和类似arrhenius的温度依赖性。应注意的是，通过使用该近似值，温度必须以k表示。使用方程式n
f
＝c0×
(δt
‑
δt0)
‑
q
并应用norris
‑
landzberg修正，应力和磁场条件下的加速度系数af如下：
[0049][0050][0051]
y＝ax1+bx2+cx3
ꢀꢀ
(3)
[0052]
式中，af，指加速因子；
△
t1为加速温度循环中高低温差；
△
t2为常规温度循环中高低温差；f1指加速温度循环中的温变速率；f2指常规温度循环中温变速率；t1指加速温度循环中高温值；t2指常规温度循环中高温值；eaa为激活能(ev)，玻尔兹曼常数k＝8.617*10
‑
5ev/℃；m、n为常数，依材料而变化，snpb焊点的典型n值为1.9，典型m值为1/3。且根据jedec jep122h
‑
2016，snpb焊点疲劳裂纹扩展失效机理的激活能为0.122。
[0053]
arrhenius模型
[0054]
高温能促进器件内部物理化学反应的速率，加快器件失效。十九世纪九十年代，阿伦尼斯研究发现了其中的规律。并在大量数据的基础上，根据经验提出了如下模型：
[0055][0056]
式中dm/dt为敏感参数的退化速率；a为待定参数，ea为激活能(ev)玻尔兹曼常数k＝8.617*10
‑
5ev/℃，t是绝对温度(k)。取对数得：
[0057][0058]
ξ为器件寿命，由上式可知寿命特征对数与温度倒数成线性关系，加速系数公式如下：
[0059][0060]
lawson湿度模型：
[0061]
lawson模型将％rh的拟合参数与加速度模型的arrhenius部分结合起来。它加上一个拟合系数，加速度系数变为：
[0062][0063]
y＝ax1+bx2
ꢀꢀ
(8)
[0064]
b＝4.4e
‑
4，取决于腐蚀特性；rh＝相对湿度，以百分比表示，％(注：100％＝饱和)；eaa级＝表观活化能，0.64ev，取决于腐蚀特性；k＝玻耳兹曼常数；t＝温度(k)。
[0065]
所述步骤(5)和(6)中，依据多组试验数据记录结果，其试验事件记录图如图2所示，只选择主要失效机理进行统计分析，其余作为删失数据。采用极大似然法(mle)估计寿命分布模型参数，建立寿命分布模型，可使用数据统计分析软件jmp，对主要失效机理数据进行多种典型失效分布模型的分析拟合，包括weibull分布、对数正态分布、对数分布，如图3所示，依据不同寿命分布模型所得的aicc值，选取最佳拟合寿命分布模型。
[0066]
选定95％置信度下，寿命分布模型估算下限得出的90％可靠度计算tr(即b10)，代入加速模型公式估算模型参数，所得加速模型为此批集成电路适用性模型，加速模型多元线性参数拟合示意图如图4所示，需注意多元线性回归相关系数r2(rsq)取值越接近1，代表拟合优度越好。
[0067]
最后，可依据推算出的适用性加速模型，计算在一定载荷作用下，非气密互连凸点90％可靠度下的贮存寿命，试验过程中增加试验样品可增加计算结果的精确度。
[0068]
本发明采用基于失效机理的半导体元器件寿命预测法，记录失效数据，并依次对时效样品进行分析，按照失效机理进行分类，可分为imc kirkendall空洞、imc脆性开裂、pbsn焊点疲劳开裂，选定主要失效机理，将其余失效数据判定为搁置数据，针对搁置数据计算调整秩，再代入计算中位秩，进而构造威布尔概率纸，从失效机理本质出发，仅需要对少量产品样品进行分析，不必像传统数理统计方法需要对大批量产品的失效数据进行统计，更加高效经济且科学。
[0069]
本发明虽然已以较佳实施例公开如上，但其并不是用来限定本发明，任何本领域技术人员在不脱离本发明的精神和范围内，都可以利用上述揭示的方法和技术内容对本发明技术方案做出可能的变动和修改，因此，凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化及修饰，均属于本发明技术方案的保护范围。