增强旋转机械故障信号特征的盲解卷积算法

1.本发明涉及基于深度学习的旋转机械故障诊断计算技术领域，尤其是一种增强旋转机械故障信号特征的盲解卷积算法。


背景技术：

2.齿轮箱和轴承是旋转机械的重要部件，它们的失效是造成机械故障最常见的原因。为了减少安全隐患，保证设备正常运行，对旋转机械的齿轮箱和轴承等部件进行状态监测尤为重要。齿轮箱或者轴承故障形成后，会产生将周期性的瞬态脉冲。然而由于受到传输路径和环境噪声的影响，振动传感器所采集的信号故障脉冲大幅度衰减，这给故障分析带来了很大阻碍。
3.盲解卷积旨求解一个逆fir滤波器对原始信号滤波，最大限度地恢复由故障激发的脉冲特征。通过最大化滤波信号的某项指标求解滤波器系数，这样的指标通常被称为最大化准则。不同盲解卷积算法的主要区别在于最大化准则不同。例如，基于峭度最大化的盲解卷积算法
‑
med；基于相关峭度最大化的盲解卷积算法
‑
mckd；基于d范数最大化的盲解卷积算法
‑
omed等。这些算法需要人为推导最大化准则对滤波器系数的偏导数，之后进一步推导出滤波器系数的迭代更新公式，最后多次迭代求解滤波器系数和滤波信号。这种求解过程需要人为推导滤波器系数的迭代更新公式，计算过程复杂，并且基于不同最大化准则的盲解卷积算法迭代更新公式不能通用，有些最大化准则甚至无法推导出迭代公式，这极大程度的限制了不同场景下最大化准则的选择和设计；另一方面，盲解卷积本质是非凸优化问题的求解，常规的盲解卷积算法在解空间搜索到一个极大值便会终止，无法继续搜索更优的解，因此常规的盲解卷积算法性能有限。
4.研究一种基于不同最大化准则的盲解卷积通用解法能保证最大化准则设计的灵活性，满足各种场合旋转机械故障诊断的需求。优化迭代求解过程，提升盲解卷积算法的性能，对于提高旋转机械故障诊断的精度具有重大意义。


技术实现要素：

5.针对现有技术的缺陷，本发明提供一种增强旋转机械故障信号特征的盲解卷积算法，解决现有盲解卷积算法精度不高，适用范围小的问题。
6.本发明采用的技术方案如下：
7.一种增强旋转机械故障信号特征的盲解卷积算法，其特征在于，包括以下步骤：
8.s1：构建多个级联的fir滤波器，根据原始振动信号的特征确定盲解卷积算法的最大化准则，将最大化准则作为目标函数；
9.s2：利用所述级联的fir滤波器依次对原始振动信号进行卷积运算，得滤波后的信号，计算滤波后的信号的目标函数值；
10.s3：采用后向自动微分算法计算当前迭代轮次下目标函数对滤波器的梯度；
11.s4：更新各滤波器的值；
12.s5：重复s2
‑
s4，达到最大迭代次数后，输出最终的滤波后的信号。
13.其进一步技术方案为：
14.利用n个级联的fir滤波器{f1,f2,
…
,f
n
‑1,f
n
}依次对原始振动信号进行卷积运算，公式如下：
15.s1＝f1*x,s2＝f2*s1,
…
,s
n
‑1＝f
n
‑1*s
n
‑2,s
n
＝f
n
*s
n
‑116.其中，s
i
表示第i个滤波器的输出，i∈[1,n]，*表示卷积运算，s
n
为原始振动信号x经n个滤波器依次滤波的滤波后的信号；
[0017]
根据所确定的最大化准则而确定的所述目标函数为j，计算s
n
的目标函数值为j(s
n
)。
[0018]
所述更新各滤波器的值，包括以下步骤：
[0019]
计算一阶动量和二阶动量：
[0020]
m
t
＝β1·
m
t
‑1+(1
‑
β1)
·
g
t
,v
t
＝β2·
v
t
‑1+(1
‑
β2)
·
g
t2
[0021]
其中，β1为一阶动量衰减系数，β2为二阶动量衰减系数，g
t
为采用后向自动微分算法计算的当前迭代次数下目标函数值j(s
n
)对滤波器的梯度，下标t表示第t次迭代；下标t
‑
1表示第t
‑
1次迭代；
[0022]
更新所有滤波器的值：
[0023][0024]
其中θ
t
＝{f1,f2,
…
,f
n
‑1,f
n
}表示第t轮迭代下所有滤波器的值，α表示学习率，ε＝10
‑8。
[0025]
梯度g
t
的计算公式如下：
[0026][0027]
其中，j代表所述j(s
n
)，t表示当前迭代轮次，n即为滤波器数量。
[0028]
本发明的有益效果如下：
[0029]
本发明构建多个级联的fir滤波器，采用后向自动微分算法，能够在解空间中搜索到一个较优的解，同时可以根据具体情况选择最大化准则，最大限度地恢复旋转机械故障信号瞬态脉冲，提高旋转机械故障诊断的精度和准确性。
[0030]
本发明采用后向自动微分算法代替梯度公式的手工推导，使得基于不同最大化准则的盲解卷积迭代算法可以通用，满足最大化准则设计的灵活性要求。
[0031]
本发明采用滤波器级联的方法对原始信号滤波，使得盲解卷积算法的性能大幅提高。
附图说明
[0032]
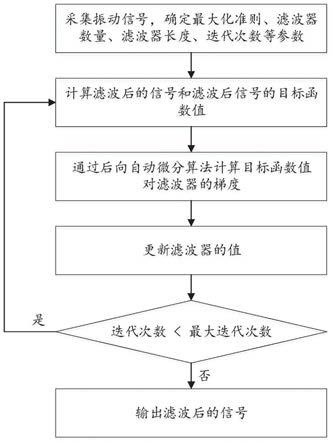
图1为本发明的流程示意图。
[0033]
图2为本发明具体实施例所采集旋转机械滚动轴承外圈故障信号。
[0034]
图3为本发明具体实施例迭代过程中滤波后信号的最大化准则变化曲线。
[0035]
图4为本发明具体实施例计算所得滤波后的信号。
[0036]
图5为本发明具体实施例计算所得滤波后的信号的包络谱。
具体实施方式
[0037]
以下结合附图说明本发明的具体实施方式。
[0038]
本技术的一种增强旋转机械信号故障特征的盲解卷积算法，可参考图1，具体包括以下步骤：
[0039]
s1：构建多个级联的fir滤波器，根据原始振动信号x的特征确定盲解卷积算法的最大化准则，将最大化准则作为目标函数j；
[0040]
具体包括：
[0041]
s11：通过加速度传感器采集旋转机械的原始振动信号x作为盲解卷积算法的原始输入，
[0042]
x＝[x1,x2,
…
,x
n
‑1,x
n
]
ꢀꢀ
(1)
[0043]
其中x
i
代表原始振动信号的每一个数据值，n表示信号的长度。
[0044]
s12：采用服从标准正态分布的随机数初始化滤波器：
[0045]
θ0＝{f1,f2,
…
,f
n
‑1,f
n
}
ꢀꢀ
(2)
[0046]
其中，n为滤波器数量,n≥2，θ代表所有滤波器，下标“0”表示进行迭代之前的初始化操作，其中，每一个滤波器f都有l个系数，即,
[0047][0048]
l表示滤波器的长度；
[0049]
s13：指定最大迭代次数m，初始化一阶动量m和二阶动量v：
[0050]
m0＝0,v0＝0
ꢀꢀ
(4)
[0051]
s14：确定最大化准则函数表达式，将其作为目标函数j；
[0052]
s2：利用上述级联的fir滤波器依次对原始振动信号x进行卷积运算，得滤波后的信号，计算滤波后的信号的目标函数值；
[0053]
具体包括：
[0054]
s21：采用n个级联的fir滤波器{f1,f2,
…
,f
n
‑1,f
n
}依次对原始振动信号x进行滤波，公式如下：
[0055]
s1＝f1*x,s2＝f2*s1,
…
,s
n
‑1＝f
n
‑1*s
n
‑2,s
n
＝f
n
*s
n
‑1ꢀꢀ
(5)
[0056]
s
i
表示第i个滤波器的输出，i∈[1,n]，*表示卷积运算，s
n
为原始振动信号x经n个滤波器依次滤波后的信号；
[0057]
卷积运算采用矩阵形式的表达如下：
[0058]
y＝f*x＝x
t
f
ꢀꢀ
(6)
[0059]
其中，x是通过原始振动信号x构建的矩阵，表达式如下：
[0060][0061]
f代表某个滤波器，表达式为公式(3)；
[0062]
原始振动信号x的表达式为公式(1)；
[0063]
s22：计算s
n
的目标函数值为j(s
n
)；
[0064]
s3：采用后向自动微分算法计算当前迭代轮次t下目标函数值对滤波器的梯度g
t
；
[0065][0066]
其中，g
t
为梯度，j表示上述j(s
n
)，t表示当前迭代轮次，f表示滤波器，n如上所述为滤波器数量。
[0067]
s4：更新所有滤波器的值；
[0068]
具体如下：
[0069]
计算一阶动量和二阶动量：
[0070]
m
t
＝β1·
m
t
‑1+(1
‑
β1)
·
g
t
,v
t
＝β2·
v
t
‑1+(1
‑
β2)
·
g
t2
ꢀꢀ
(8)
[0071]
其中，g
t
如上所述为梯度；β1为一阶动量衰减系数，取值为0.9，β2为二阶动量衰减系数，取值为0.999；下标t表示第t次迭代；下标t
‑
1表示第t
‑
1次迭代；
[0072]
更新所有滤波器的值：
[0073][0074]
其中θ
t
＝{f1,f2,
…
,f
n
‑1,f
n
}表示第t轮迭代下所有滤波器的值，α表示学习率，设置为0.01；为防止除数为0，设置ε＝10
‑8。
[0075]
s5：迭代执行s2
‑
s4，每迭代一次，迭代轮次t加1，当迭代轮次t达到最大迭代次数时结束迭代，输出最终滤波后的信号s
n
。采用故障诊断技术分析旋转机械的故障类型和故障程度。
[0076]
以下通过具体实施例进一步说明本技术的方案：
[0077]
通过加速度传感器采集滚动轴承外圈故障信号，轴转速为1649r/min，对应的内圈和外圈故障特征频率分别为148.8hz，98.5hz。采样频率为10240hz，信号持续0.6秒，采集的原始振动信号如图2所示。由图2可知原始信号中故障脉冲序列被噪声成分淹没。
[0078]
设置最大迭代次数m＝100。设置算法的参数，滤波器长度l＝30，滤波器个数n＝2，采用服从标准正态分布的随机数初始化滤波器f1,f2，将峭度指标作为最大化准则。
[0079]
其中，峭度的表达式为：
[0080]
[0081]
y
n
代表信号y的每一个数据值，n为信号y的数据值的数量，下标n∈[1,n]。
[0082]
则目标函数为：
[0083][0084]
步骤s2
‑
s4表示一次迭代过程，步骤s2计算了本次迭代的滤波后的信号s2和目标函数值j(s2)，s3和s4用于更新滤波器的值。随着迭代过程的进行，s2的峭度逐渐增大并最终收敛，如图3所示。
[0085]
达到最大迭代次数m时退出迭代，输出滤波后的信号s2，如图4所示。滤波后的信号噪声幅值较小，故障脉冲序列清晰。
[0086]
后续通过包络分析技术，分析滚动轴承的故障类型和故障程度，滤波后的信号的包络谱如图5所示。其中外圈故障特征频率及其倍频成分清晰可见，说明旋转机械的滚动轴承发生了较严重的外圈故障。