一种改进的鲁棒主成分分析的运动目标检测方法

1.本发明涉及技术领域，具体而言涉及一种改进的鲁棒主成分分析的运动目标检测方法。


背景技术：

2.运动目标检测一直是计算机视觉领域的重要课题。传统的运动目标检测技术包括高斯混合模型法、vibe法、光流法和主成分分析法等，但是这些方法是针对单像素的，较少考虑运动场景的结构化信息等其他关键因素。为了解决此类问题，人们将主成分分析方法引入到运动目标检测中并取得了较好的效果，但是该类方法是针对背景建模的，对于腐蚀严重的场景的运动目标检测的效果较差。在此背景下，鲁棒主成分分析方法被研究并应用于运动目标检测中，例如主成分追踪算法等，但是此类算法是一个有偏估计，非最优，所以对于一些特定的场景的运动目标检测效果欠佳，例如存在树枝摇曳，水纹波动等的场景。在此背景下，逼近程度高的非凸函数被引入到鲁棒主成分分析模型中，并取得了较好的效果，例如截断核范数方法、去分解方法、非凸非光滑的低秩稀疏方法等。
3.公开号为cn111428795a的发明中公开了一种改进的非凸鲁棒主成分分析方法，将待处理视频转化为一个大小为m行，n列的二维矩阵d；将二维矩阵d输入至预先构建的改进的非凸鲁棒主成分分析方法的模型，输出为对应于视频背景的低秩矩阵b和对应于视频前景的稀疏矩阵f，所述改进的非凸鲁棒主成分分析方法的模型采用广义非凸核范数作为模型的秩函数，采用结构化稀疏范数作为模型中的10范数。该发明能够更好的逼近传统鲁棒主成分分析方法中的秩函数，提高了鲁棒主成分分析方法在视频的前背景分离中的效果；引入结构化稀疏范数，为视频的前景建立了结构化的稀疏模型，极大的丰富了模型的结构化信息，提高了鲁棒主成分分析方法对光照、波动等因素影响的视频的前背景分离的效果。但仍然缺乏对运动目标的深层次分析效果。


技术实现要素：

4.本发明针对现有技术中的不足，提供一种改进的鲁棒主成分分析的运动目标检测方法，同时采用非凸γ范数和拉普拉斯尺度混合尺度，以更好地逼近传统鲁棒主成分分析模型中的秩函数和稀疏度函数；引入的显著性映射矩阵更能有效的判别哪些像素属于运动目标部分，对运动目标检测的效果更优。
5.为实现上述目的，本发明采用以下技术方案：
6.第一方面，本发明实施例提出了一种改进的鲁棒主成分分析的运动目标检测方法，所述检测方法包括以下步骤：
7.s1，基于改进的鲁棒主成分分析方法构建运动目标检测模型：
[0008][0009]
[0010]
其中d视频对应的观测矩阵，l∈r
m
×
n
为观测矩阵中对应的低秩背景矩阵，||l||
γ
为矩阵l的γ范数，j＝1，2，
…
，mn，ψ
j
是尺度为1的拉普拉斯分布，θ
j
是一个正随机变量，ξ是一个极小的正数，w是显著性映射矩阵，ψ＝[ψ1，ψ2，
…
，ψ
mn
]，θ＝[θ1，θ2，
…
，θ
mn
]；m和n分别是观测矩阵的行数和列数；
[0011]
s2，将待处理视频转换成对应的观测矩阵，采用交替方向乘子法求解运动目标检测模型，提取对应视频中处于运动状态的前景目标，并计算检测该运动目标时的f
‑
measure值和时间值，对运动目标检测模型进行验证。
[0012]
可选地，所述运动目标检测模型对应的增广拉格朗日函数为：
[0013][0014]
式中，μ＞0是惩罚因子，y是拉格朗日乘子，<，>是矩阵内积，||
·
||
f
为frobenius范数。可选地，步骤s2中，采用交替方向乘子法求解运动目标检测模型的过程包括以下步骤：
[0015]
s21，固定变量ψ、θ、y和μ，计算得到第k+1步的矩阵变量l
k+1
为：
[0016][0017]
式中，μ
k
是惩罚参数μ的第k步的值，y
k
是第k步的增广拉格朗日乘子，ψ
k
是ψ的第k步的值，θ
k
是θ第k步的值；
[0018]
s22，固定变量l、ψ、y和μ，计算得到第k+1步的矩阵变量θ
k+1
：
[0019][0020]
最终得到：
[0021][0022]
其中，θ
j，1
、θ
j，2
分别为f(θ
j
)的两个驻点：
[0023][0024]
式中，ξ是一个极小的正数，是第k步矩阵ψ
k
的第j个标量元素ψ
j
的取值，是第k+1步矩阵l
k+1
的第j个标量元素的取值，是第k步矩阵y
k
的第j个标量元素的取值，d
j
是矩阵d的第j个标量元素的取值，
[0025]
s23，固定变量l、θ、y和μ，计算得到第k+1步的矩阵变量ψ
k+1
：
[0026][0027]
最终得到：
[0028][0029]
式中，为软阈值收缩算子；
[0030]
s24，固定其它变量，更新乘子变量y及其惩罚参数μ进行更新，计算得到第k+1步的增广拉格朗日乘子：
[0031][0032]
μ
k+1
＝min(ρμ
k
，μ
max
)
[0033]
式中，ρ＞1是步长因子；μ
max
是惩罚参数μ的最大值。
[0034]
可选地，步骤s21中，采用凸差分方法求解得到矩阵变量l
k+1
。
[0035]
可选地，步骤s22中，将矩阵变量θ
k+1
的求解问题转换为求解矩阵θ
k+1
的每个标量元素的最小值问题，即：
[0036][0037]
其中
[0038]
通过求解每个标量元素θ
i
的最小值问题，其中f(θ
j
)是相应的目标函数，最终得到：
[0039][0040]
其中，θ
j，1
、θ
j，2
分别为f(θ
j
)的两个驻点：
[0041][0042]
可选地，步骤s23中，将矩阵变量ψ
k+1
的求解问题转换为求解矩阵ψ
k+1
的每个标量元素的最小值问题，即：
[0043][0044]
最终得到：
[0045][0046]
其中为软阈值收缩算子。
[0047]
本发明提出了一种改进的鲁棒主成分分析的运动目标检测系统，该方法分别采用非凸γ范数和拉普拉斯尺度混合尺度分别逼近传统鲁棒主成分分析模型中的秩函数和稀疏度函数，同时将显著性映射矩阵引入到该模型中，采用交替方向乘子法对其求解。最后，将该方法应用到运动目标检测实验中，进一步证明本文提出算法的有效性和优越性。
附图说明
[0048]
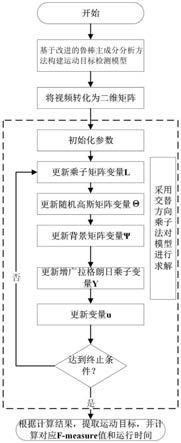
图1是本发明实施例的改进的鲁棒主成分分析的运动目标检测方法流程图。
[0049]
图2是本发明实施例的检测方法和其他现有检测方法提取的运动目标视觉对比图。
[0050]
图3是本发明实施例的检测方法和其他现有检测方法提取运动目标对应的量化的f
‑
measure值比对结果示意图。
[0051]
图4是本发明实施例的检测方法和其他现有检测方法提取运动目标对应的量化的运行时间值对比结果示意图。
具体实施方式
[0052]
现在结合附图对本发明作进一步详细的说明。
[0053]
需要注意的是，发明中所引用的如“上”、“下”、“左”、“右”、“前”、“后”等的用语，亦仅为便于叙述的明了，而非用以限定本发明可实施的范围，其相对关系的改变或调整，在无实质变更技术内容下，当亦视为本发明可实施的范畴。
[0054]
图1是本发明实施例的改进的鲁棒主成分分析的运动目标检测方法流程图。参见图1，该检测方法包括以下步骤：
[0055]
s1，基于改进的鲁棒主成分分析方法构建运动目标检测模型：
[0056][0057][0058]
其中d视频对应的观测矩阵，l∈r
m
×
n
为观测矩阵中对应的低秩背景矩阵，||l||
γ
为矩阵l的γ范数，j＝1，2，
…
，mn，ψ
j
是尺度为1的拉普拉斯分布，θ
j
是一个正随机变量，ξ是一个极小的正数，w是显著性映射矩阵，ψ＝[ψ1，ψ2，
…
，ψ
mn
]，θ＝[θ1，θ2，
…
，θ
mn
]。
[0059]
s2，将待处理视频转换成对应的观测矩阵，采用交替方向乘子法求解运动目标检测模型，提取对应视频中处于运动状态的前景目标，并计算检测该运动目标时的f
‑
measure值和时间值，对运动目标检测模型进行验证。
[0060]
可选地，所述运动目标检测模型对应的增广拉格朗日函数为：
[0061][0062]
式中，μ＞0是惩罚因子，y是拉格朗日乘子，<，>是矩阵内积。
[0063]
可选地，步骤s2中，采用交替方向乘子法求解运动目标检测模型的过程包括以下步骤：
[0064]
s21，固定变量ψ、θ、y和μ，计算得到矩阵变量l
k+1
为：
[0065]
[0066]
示例性地，采用凸差分方法对上式进行求解，得到矩阵变量l
k+1
。
[0067]
s22，固定变量l、ψ、y和μ，计算得到矩阵变量θ
k+1
：
[0068][0069]
示例性地，将矩阵变量θ
k+1
的求解问题转换为求解矩阵θ
k+1
的每个标量元素的最小值问题，即：
[0070][0071]
其中
[0072]
通过求解每个标量元素θ
i
的最小值问题，其中f(θ
j
)是相应的目标函数，最终得到：
[0073][0074]
其中，θ
j，1
、θ
j，2
分别为f(θ
j
)的两个驻点：
[0075][0076]
s23，固定变量l、θ、y和μ，计算得到矩阵变量ψ
k+1
：
[0077][0078]
示例性地，将矩阵变量ψ
k+1
的求解问题转换为求解矩阵ψ
k+1
的每个标量元素的最小值问题，即：
[0079][0080]
最终得到：
[0081][0082]
式中，为软阈值收缩算子。
[0083]
s24，固定其它变量，更新乘子变量y及其惩罚参数μ进行更新，计算得到：
[0084][0085]
μ
k+1
＝min(ρμ
k
，μ
max
)
[0086]
式中，p＞1是步长因子。
[0087]
本实施例提供一种改进的鲁棒主成分分析的运动目标检测方法，基于改进的鲁棒主成分分析方法构建运动目标检测模型，并采用交替方向乘子法求解运动目标检测模型，该运动目标检测模型将提出的改进的鲁棒主成分分析方法对运动目标进行检测，提取出对应视频中的运动的前景目标。图2是本发明实施例的检测方法和其他现有检测方法提取的运动目标视觉对比图，从视觉角度对比凸显本实施例提出的基于改进的鲁棒主成分分析方法构建的运动目标检测模型的优越效果。参见图3和图4，在实验过程中计算采用提出的改进的鲁棒主成分分析方法对运动目标进行检测时的f
‑
measure值和时间值，从量化角度直观凸显本实施例公开的运动目标检测模型相比现有技术具有更加优越的检测效果。这也使得本实施例可以随时定量验证运动目标检测模型的有效性，进而反哺模型求解过程。
[0088]
以上仅是本发明的优选实施方式，本发明的保护范围并不仅局限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理前提下的若干改进和润饰，应视为本发明的保护范围。