基于神经网络的多工况一维波动方程求解方法

1.本发明属于地震工程领域，具体涉及一种基于神经网络求解多工况一维波动方程进而实现地震动模拟的方法。


背景技术：

2.伴随着经济发展，城镇化速度加快，特大城市及城市群的出现，这些都对单体结构，建筑群乃至整座城市的抗震韧性提出了更高的挑战。地震动场的建立是进行结构抗震韧性设计、评估的前提。如何快速、准确的模拟地震动场也是学界一直在研究的热门。地震动场与地震波在介质中的传播息息相关。根据表示定理，地震动可以表示为格林函数与震源的卷积，而格林函数通常通过求解波动方程得到，因此求解波动程是地震动模拟中至关重要的一步。
3.近年来随着计算机技术的发展，神经网络被越来越广泛的应用于地球物理、地震工程等领域，然而大多神经网络的训练需要大量的训练数据，不同工况需要训练不同的神经网络模型，耗时费力，并且得到的“黑箱”模型缺乏物理规律的限制，难以解释。


技术实现要素：

4.本发明的目的是为了解决神经网络求解不同工况下的一维波动方程耗时费力的问题，而提供一种基于神经网络的多工况一维波动方程求解方法。
5.本发明基于神经网络的多工况一维波动方程求解方法按照以下步骤实现：
6.步骤一、建立控制方程，各向同性介质中一维地震波动方程如下：
[0007][0008]
其中v表示波速，u表示(x,t)坐标下质点的位移；
[0009]
步骤二、确定求解域与残差点数量：
[0010]
设定x的求解域为[0,1]，t的求解域为[0,1]，残差点数量为400～800个；
[0011]
步骤三、建立深度神经网络：
[0012]
建立包含6个隐藏层的全连接层神经网络，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0013]
步骤四、损失函数设计：
[0014]
使用损失函数表征是否训练收敛，损失函数的公式如下：
[0015][0016]
其中u
real
代表位移真实值；
[0017]
步骤五、网络训练：
[0018]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，再使用l
‑
bfgs
‑
b算法进行求解(精细训练)，从而完成多工况一维波动方程
求解。
[0019]
本发明基于神经网络的多工况一维波动方程求解方法按照以下步骤实现：
[0020]
步骤一、建立控制方程：各向同性介质中一维地震波动方程，该方程考虑y方向位移引起的x方向的应力：
[0021][0022][0023]
其中v
p
为地震p波波速，v
s
为地震s波波速，ρ为介质密度，σ
xx
和σ
xy
为x方向上的两个应力分量，u
x
表示x方向的位移，u
y
表示y方向的位移；
[0024]
步骤二、确定求解域与残差点数量：
[0025]
设定x的求解域为[0,1],t的求解域为[0,1]，v
p
的取值为0～2km/s，v
s
的取值为0～2km/s，残差点数量取为800～1200个；
[0026]
步骤三、建立深度神经网络：
[0027]
建立包含6个隐藏层的全连接层神经网络，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0028]
步骤四、损失函数设计：
[0029]
使用损失函数表征是否训练收敛，损失函数的公式如下：
[0030][0031]
其中u
xreal
为x方向位移真实值，u
yreal
为y方向位移真实值，σ
xxreal
为x方向上的位移引起的x方向应力的真实值，σ
xyreal
为y方向上的位移引起的x方向应力的真实值；
[0032]
步骤五、网络训练：
[0033]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，再使用l
‑
bfgs
‑
b算法进行求解(精细训练)，从而完成多工况一维波动方程求解。
[0034]
本发明将波速作为输入，提出一种基于神经网络的一维波动方程求解方法，使得模型能学习到不同工况对于方程解的影响，在保持高求解精度的前提下，泛定方程作为求解的基本方程，控制着输入数据与输出数据间最基本的数理规律，应力条件的加入使得方程的求解受到了具体物理过程的控制，在神经网络这一数据驱动的方法里引入了物理条件后，使得训练收敛更快，模型对数据的以来依赖更少，同时增加了本发明一维波动方程求解方法的可解释性。
[0035]
本发明采用一维波动方程作为控制方程，将不同波速输入网络进行训练，使网络能够进行多工况下的方程求解，在保证了求解精度的同时，省去了针对不同工况不断训练网络的繁琐。
[0036]
本发明提出了一种求解一维波动方程的新方法，以应用于地震学、地震监测等领域。
附图说明
[0037]
图1为实施例基于神经网络的多工况一维波动方程求解方法的总体框架流程图；
[0038]
图2为实施例一中求解一维波动方程的深度神经网络结构图；
[0039]
图3为实施例二中求解一维波动方程的深度神经网络结构图；
[0040]
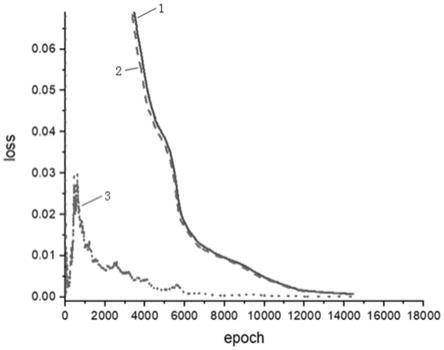
图4为实施例一中损失函数loss的下降曲线图，其中1代表训练总误差，2代表数据误差，3代表方程误差；
[0041]
图5为实施例二中损失函数loss下降曲线图，图中1代表训练总误差，2代表x方向位移数据误差，3代表y方向位移数据误差，4代表x方向位移引起的x方向应力数据误差；5代表y方向位移引起的x方向应力数据误差，6代表x方向位移引起的x方向应力方程误差，7代表y方向位移引起的x方向应力方程误差，8代表x方向位移方程误差，9代表y方向位移方程误差；
[0042]
图6为实施例一中求解结果与解析解对比散点图，其中1(u
*
)代表求解结果，2(u)代表解析解；
[0043]
图7为实施例二中x方向位移求解结果与解析解对比散点图，求解结果与解析解基本重合，ux
*
代表求解结果，ux代表解析解；
[0044]
图8为实施例二中y方向位移求解结果与解析解对比散点图，求解结果与解析解基本重合，uy
*
代表求解结果，uy代表解析解；
[0045]
图9为实施例二中x方向位移引起的x方向应力求解结果与解析解对比散点图，求解结果与解析解基本重合，其中sigmaxx
*
代表求解结果，sigmaxx代表解析解；
[0046]
图10为实施例二中y方向位移引起的x方向应力求解结果与解析解对比散点图，求解结果与解析解基本重合，其中sigmaxy
*
代表求解结果，sigmaxy代表解析解；
[0047]
图11为实施例一中的绝对误差分布图；
[0048]
图12为实施例二中x方向位移的绝对误差分布图；
[0049]
图13为实施例二中y方向位移的绝对误差分布图；
[0050]
图14为实施例二中x方向位移引起的x方向应力的绝对误差分布图；
[0051]
图15为实施例二中y方向位移引起的x方向应力的绝对误差分布图。
具体实施方式
[0052]
具体实施方式一：本实施方式基于神经网络的多工况一维波动方程求解方法按照以下步骤实施：
[0053]
步骤一、建立控制方程，各向同性介质中一维地震波动方程如下：
[0054][0055]
其中v表示波速，u表示(x,t)坐标下质点的位移；
[0056]
步骤二、确定求解域与残差点数量：
[0057]
设定x的求解域为[0,1]，t的求解域为[0,1]，残差点数量为400～800个；
[0058]
步骤三、建立深度神经网络：
[0059]
建立包含6个隐藏层的全连接层神经网络，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0060]
步骤四、损失函数设计：
[0061]
使用损失函数表征是否训练收敛，损失函数的公式如下：
[0062][0063]
其中u
real
代表位移真实值；
[0064]
步骤五、网络训练：
[0065]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，再使用l
‑
bfgs
‑
b算法进行求解，从而完成多工况一维波动方程求解。
[0066]
具体实施方式二：本实施方式与具体实施方式一不同的是步骤二中残差点数量为500个。
[0067]
具体实施方式三：本实施方式与具体实施方式一或二不同的是步骤三中每个隐藏层包含40个神经元。
[0068]
具体实施方式四：本实施方式与具体实施方式一至三之一不同的是步骤五中所述的adam自适应优化函数算法如下：
[0069]
(1)计算梯度的一阶矩估计和二阶矩估计，计算公式为：
[0070]
m
t
＝β1·
m
t
‑1+(1
‑
β1)
·
g
t
，ν
t
＝β2·
ν
t
‑1+(1
‑
β2)
·
g
t2
；
[0071]
式中，g
t
为梯度，其中m
t
为梯度的t时刻平均值，ν
t
为梯度的t时刻非中心方差值，m
t
‑1为梯度的t
‑
1时刻平均值，v
t
‑1为梯度的t
‑
1时刻非中心方差值，矩估计的指数衰减速率β1和β2在区间[0,1)内，β1取0.9，β2取0.999；
[0072]
(2)对一阶矩估计和二阶矩估计的校正，计算公式为：
[0073][0074]
(3)参数更新的最终公式为：
[0075][0076]
式中，θ
t
为更新的参数，η为学习率，ε为用于数值稳定的小常数，ε取10
‑8。
[0077]
具体实施方式五：本实施方式与具体实施方式一至四之一不同的是步骤五中预训练轮次10000次，批大小(batchsize)为1000，学习率为0.0025。
[0078]
具体实施方式六：本实施方式基于神经网络的多工况一维波动方程求解方法按照以下步骤实现：
[0079]
步骤一、建立控制方程：各向同性介质中一维地震波动方程，该方程考虑y方向位移引起的x方向的应力：
[0080][0081][0082]
其中v
p
为地震p波波速，v
s
为地震s波波速，ρ为介质密度，σ
xx
和σ
xy
为x方向上的两个应力分量，u
x
表示x方向的位移，u
y
表示y方向的位移；
[0083]
步骤二、确定求解域与残差点数量：
[0084]
设定x的求解域为[0,1],t的求解域为[0,1]，v
p
的取值为0～2km/s，v
s
的取值为0～2km/s，残差点数量为800～1200个；
[0085]
步骤三、建立深度神经网络：
[0086]
建立包含6个隐藏层的全连接层神经网络，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0087]
步骤四、损失函数设计：
[0088]
使用损失函数表征是否训练收敛，损失函数的公式如下：
[0089][0090]
其中u
xreal
为x方向位移真实值，u
yreal
为y方向位移真实值，σ
xxreal
为x方向上的位移引起的x方向应力的真实值，σ
xyreal
为y方向上的位移引起的x方向应力的真实值；
[0091]
步骤五、网络训练：
[0092]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，再使用l
‑
bfgs
‑
b算法进行求解，从而完成多工况一维波动方程求解。
[0093]
具体实施方式七：本实施方式与具体实施方式六不同的是步骤二中残差点数量为1000个。
[0094]
具体实施方式八：本实施方式与具体实施方式六或七不同的是步骤三中每个隐藏层包含40个神经元。
[0095]
具体实施方式九：本实施方式与具体实施方式六至八之一不同的是步骤五中预训练轮次10000次。
[0096]
具体实施方式十：本实施方式与具体实施方式九不同的是预训练批大小(batchsize)为1000，学习率为0.0025。
[0097]
实施例一：本实施例基于神经网络的多工况一维波动方程求解方法按照以下步骤实施：
[0098]
步骤一、建立控制方程：各向同性介质中一维地震波动波动方程：
[0099][0100]
其中v表示波速，u表示(x,t)坐标下质点的位移；
[0101]
步骤二、确定求解域与残差点数量：
[0102]
设定x的求解域为[0,1],t的求解域为[0,1]，残差点数量为500个；
[0103]
步骤三、建立深度神经网络：
[0104]
建立包含6个隐藏层的全连接层神经网络，每个隐藏层包含40个神经元，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0105]
步骤四、损失函数设计：
[0106]
使用损失函数表征是否训练收敛，损失函数包含数据误差与方程误差(只包含位移)，损失函数的公式如下：
[0107][0108]
其中u
real
代表位移真实值；
[0109]
步骤五、网络训练：
[0110]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，训练轮次10000次，批大小(batchsize)为1000，学习率为0.0025，再使用l
‑
bfgs
‑
b算法进行求解，从而完成多工况一维波动方程求解。
[0111]
该神经网络训练数据源于固定区间内的随机采样，本实施例完成多工况一维波动方程求解后能够获得格林函数，从而实现地震动模拟，图4表示训练结束时，网络误差趋于稳定，图6说明网络的求解结果与解析解吻合较好，图11展示了绝对误差的分布，说明误差均保持在小量级。
[0112]
实施例二：本实施例基于神经网络的多工况一维波动方程求解方法按照以下步骤实现：
[0113]
步骤一、建立控制方程：各向同性介质中一维地震波动方程，该方程考虑y方向位移引起的x方向的应力：
[0114][0115][0116]
其中v
p
为地震p波波速，v
s
为地震s波波速，ρ为介质密度，σ
xx
,σ
xy
为x方向上的两个应力分量，u
x
表示x方向的位移，u
y
表示y方向的位移；
[0117]
步骤二、确定求解域与残差点数量：
[0118]
设定x的求解域为[0,1],t的求解域为[0,1]，v
p
的取值为0～2km/s，v
s
的取值为0～2km/s，残差点数量为1000个；
[0119]
步骤三、建立深度神经网络：
[0120]
建立包含6个隐藏层的全连接层神经网络，每个隐藏层包含40个神经元，采用双曲正切函数(tanh)为激活函数，得到深度神经网络模型；
[0121]
步骤四、损失函数设计：
[0122]
使用损失函数表征是否训练收敛，损失函数的公式如下：
[0123][0124]
其中u
xreal
为x方向位移真实值，u
yreal
为y方向位移真实值，σ
xxreal
为x方向上的位移引起的x方向应力的真实值，σ
xyreal
为y方向上的位移引起的x方向应力的真实值；
[0125]
步骤五、网络训练：
[0126]
以步骤四中的损失函数为目标函数进行网络的训练，采用adam自适应优化函数算法进行预训练，预训练轮次10000次，批大小(batchsize)为1000，学习率为0.0025，再使用
l
‑
bfgs
‑
b算法进行求解，从而完成多工况一维波动方程求解。
[0127]
本实施例完成多工况一维波动方程求解后能够获得格林函数，从而实现地震动模拟，图5表示训练结束时，网络误差趋于稳定，图7
‑
图10说明网络的求解结果与解析解吻合较好，图12
‑
图15展示了绝对误差的分布，说明误差均保持在小量级。