随机介质等效均匀化截面的计算方法

1.本发明涉及一种随机介质等效均匀化截面的计算方法。


背景技术：

2.弥散型燃料能够降低放射性泄漏风险，被广泛用于先进核反应堆。常见的弥散型燃料包括：高温气冷堆使用的由三层包覆各向同性(triso)燃料颗粒弥散在石墨基体构成的球形或柱状燃料元件、先进压水堆中使用全陶瓷微封装(fcm)燃料、一些研究堆或特殊用途反应堆使用的板状弥散型燃料、以及空间堆等其它新型反应堆使用的各种几何形式的弥散型燃料。
3.弥散型燃料元件的燃料区由基体和颗粒构成，是一种典型的随机介质，导致燃料栅元具有双重非均匀性，给中子输运计算带来挑战。确定论程序对随机介质的处理方法主要分为两类。第一类方法是将随机介质等效均匀化过程与对整个系统的中子输运计算过程进行耦合，即在中子输运迭代求解过程中不断更新随机介质的等效均匀化截面。该方法由sanchez和hebert等人提出和发展，代表性程序是dragon。第二类方法是预先计算随机介质的等效均匀化截面，然后使用常规的中子输运方法求解整个系统；该方法由teuchert、yamamoto、以及本发明人等人提出和发展，代表性程序是vsop和xpz。与第一类方法相比，第二类方法的实现更加简单，可以很方便地应用到已有程序中。
4.以上提及的现有技术中的中子输运计算方法请参考下列文献：
5.r.sanchez and e.masiello,“treatment of the double heterogeneity with the method of characteristics,”physor 2002,seoul,korea,october 7
‑
10(2002).
6.r.sanchez,“renormalized treatment of the double heterogeneity with the method of characteristics,”physor 2004,chicago,usa,april 25
‑
29(2004).
7.a.h
é
bert,“a collision probability analysis of the double
‑
heterogeneity problem,”nuclear science and engineering,115.2,177
‑
184(1993).
8.a.h
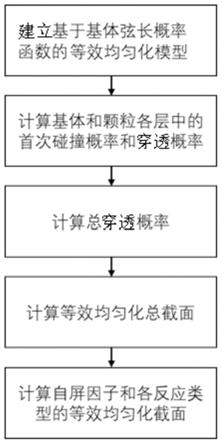
é
bert,“scattering reduction of the double
‑
heterogeneity treatment in dragon,”nuclear science and engineering,160.2,261
‑
266(2008).
9.u.hansen,and e.teuchert,“influence of coated
‑
particle structure in thermal
‑
neutron
‑
spectrum energy range,”nuclear science and engineering,44.1,12
‑
17(1971).
10.t.yamamoto,y.miyoshi and t.takeda,“extension of effective cross section calculation method for neutron transport calculations in particle
‑
dispersed media,”journal of nuclear science and technology,43.1,77
‑
87(2006).
11.本发明人于2016年提出一种计算随机介质等效均匀化截面的方法，参见d.she,z.liu,l.shi,“an equivalent homogenization method for treating the stochastic media,”nuclear science and engineering,185,351
‑
360(2017)。该方法包括构造如下圆柱模型：将包覆颗粒置于圆柱形的基体中，假设中子均匀平行穿过圆柱底面。基于该模型，
可计算得到中子在基体以及颗粒各层中的首次碰撞概率p
j
以及在整个圆柱中的总穿透概率p。然后，通过公式计算得到等效均匀化总截面，其中l为圆柱高度。
12.等效均匀化截面的计算表达式为其中下标j表示随机介质区域内的物质子区(例如基体或颗粒中的某一层)的编号，f
j
表示第j区体积份额，s
j
表示第j区的空间自屏因子，σ
j
为第j区的截面，为第j区的有效截面。
13.计算等效均匀化截面的原则是保证中子在各个子区的首次碰撞概率p
j
以及在随机介质区的总穿透概率p不变。在上述计算得到的首次碰撞概率p
j
、总穿透概率p以及等效均匀化总截面的基础上，注意到使用以下流程计算等效均匀化截面：首先，根据穿透概率p不变，计算等效均匀化总截面；然后，根据计算各子区的有效截面，以及根据计算各子区的自屏因子；最后，根据计算各反应类型的等效均匀化后截面。
14.上述方法的关键是构造了由基体与颗粒组成的圆柱模型，用平行中子束在圆柱模型中的首次碰撞过程近似替代中子在随机介质中的首次碰撞过程。在保证填充率不变的前提下，上述圆柱模型中的圆柱高度和半径可调，因此该模型实际上具有半经验性。在低填充率或混合颗粒填充情况下，该模型也存在一定局限性。
15.因此，希望提出一种物理意义更严格、精度更高、适用范围更广的计算方法，以替代采用人为构造的、存在半经验性和局限性的圆柱模型的计算方法，实现精确、高效、普适的随机介质等效均匀化处理。


技术实现要素：

16.为此，本发明提出了一种无需引入人为构造的几何模型(如上文述及的圆柱模型)而是通过严格的概率分布函数描述中子在随机介质中的首次碰撞过程的技术方案，从而使本发明的计算方法克服了半经验性、建立在严格物理意义的基础上。
17.随机介质等效均匀化主要针对热中子和中能中子，它们通常是由快中子在基体当中或在随机介质外部慢化产生。因此，热中子和中能中子在随机介质中的首次碰撞分为两个过程：第一个过程是中子在基体中均匀产生或从随机介质外部进入基体后，在基体中发生首次碰撞或穿透基体的过程；第二个过程是中子穿透基体后，在颗粒中发生首次碰撞或穿透颗粒的过程。
18.对于第一个过程，即中子穿过基体的过程，可以通过基体弦长概率分布函数f(l0)进行描述，其中l0表示中子在基体中均匀产生或从随机介质外部进入基体后距离下一个颗粒表面的距离。
19.对于第二个过程，即中子穿过颗粒的过程，通过以下两个概率进行描述：中子穿透基体后进入第k种颗粒的概率t
k
，以及中子各向同性进入颗粒k表面后在颗粒第i层发生首
次碰撞的概率。本发明的计算方法基于概率t
k
而得以直接处理多种颗粒的情形，而无需向上文述及的圆柱模型中那样进行额外处理。
20.基于上述模型，本发明提出了一种随机介质等效均匀化截面的计算方法，所述随机介质包括基体和容纳在基体内的若干种颗粒，该方法包括如下步骤：基于基体弦长概率分布函数和基体总截面计算中子在基体中的穿透概率，并根据中子在基体中的穿透概率得出中子在基体中的首次碰撞概率；基于中子在基体中的穿透概率、中子穿透基体后进入各种颗粒的概率、中子进入各种颗粒后在颗粒各层发生首次碰撞的概率计算中子在颗粒中的首次碰撞概率；基于中子在基体中的首次碰撞概率和中子在颗粒中的首次碰撞概率计算总穿透概率；以待求的等效均匀化总截面填充基体和所有颗粒，表示出中子在基体和颗粒中的穿透概率，并进而得出以颗粒半径、等效均匀化总截面表示的总穿透概率，考虑到以颗粒半径、等效均匀化总截面表示的总穿透概率应与上述的基于中子在基体中的首次碰撞概率和中子在颗粒中的首次碰撞概率计算出的总穿透概率相同，从而得到并求解关于等效均匀化总截面的非线性方程而计算出等效均匀化总截面；基于所得到的中子在颗粒中的首次碰撞概率、总穿透概率和等效均匀化总截面计算自屏因子和等效均匀化截面。
21.根据本发明的一种优选实施形式的随机介质等效均匀化截面的计算方法，其中，该方法包括如下步骤：
22.按照公式计算中子在基体中的穿透概率e0，并按照公式p0＝1
‑
e0得出中子在基体中的首次碰撞概率p0，其中，σ0为基体总截面，l0表示中子在基体中均匀产生或从随机介质外部进入基体后距离下一个颗粒表面的距离，f(l0)为基体弦长概率分布函数；
23.按照公式计算中子在颗粒中的首次碰撞概率p
k,j
，其中，t
k
为中子穿透基体后进入第k种颗粒的概率，表示中子进入颗粒k后在颗粒第i层发生首次碰撞的概率，通过已知的碰撞概率公式求得或通过构造“平行中子束穿过颗粒”的几何模型计算得出；
24.按照公式计算总穿透概率p；
25.通过求解非线性方程得出等效均匀化总截面其中，r
k
为颗粒半径，而满足是以待求的等效均匀化总截面填充基体和所有颗粒时中子在基体中的穿透概率；
26.基于首次碰撞概率p
k,j
、总穿透概率p和等效均匀化总截面计算自屏因子和等效均匀化截面。根据计算各子区的有效截面，以及根据计算各子区的自屏因子；最后，根据计算各反应类型的等效均匀化后截面。
27.在上述计算方法中，在计算得到总穿透概率p之后，由于没有一个像圆柱模型中那
样的对应的飞行距离l，因而无法通过公式直接计算等效均匀化总截面。因此，使用以下方法计算等效均匀化总截面：
28.假设待求的等效均匀化总截面为用该截面填充基体和所有颗粒。则中子在基体中的穿透概率为
29.中子在均匀化颗粒k的穿透概率为：
[0030][0031]
其中是第k种颗粒的弦长概率分布函数，r
k
是第k种颗粒的半径。
[0032]
因此，均匀化后的总穿透概率表示为：
[0033][0034]
根据总穿透概率不变的原则，即可得到关于的上述非线性方程：
[0035][0036]
基体弦长概率分布函数的具体形式可以任意选择，不影响本发明的有效性。可选的是，中子在基体中的穿透概率e0或首次碰撞概率p0或基体弦长概率分布函数f(l0)通过蒙特卡罗抽样方法直接计算出。
[0037]
根据本发明的一种优选实施形式的随机介质等效均匀化截面的计算方法，其中，基体弦长概率分布函数f(l0)按照下列公式计算：
[0038][0039]
其中，为基体平均弦长，基体平均弦长通过下列公式计算：
[0040][0041]
其中，f
k
为第k种颗粒的体积填充率，r
k
为第k种颗粒的颗粒半径。
[0042]
根据本发明的一种优选实施形式的随机介质等效均匀化截面的计算方法，其中，中子穿透基体后进入第k种颗粒的概率t
k
按照下列公式计算：
[0043][0044]
其中，f
k
为颗粒体积份额，r
k
为颗粒半径。
[0045]
根据本发明的一种优选实施形式的随机介质等效均匀化截面的计算方法，其中，中子穿透基体后进入第k种颗粒的概率t
k
通过蒙特卡罗抽样方法直接计算出。
[0046]
根据本发明的一种优选实施形式的随机介质等效均匀化截面的计算方法，其中，通过数值解法求解所述非线性方程得出等效均匀化总截面
附图说明
[0047]
下文结合附图阐释本发明的实施例。在附图中：
[0048]
图1是总体计算流程图。
[0049]
图2是用于计算首次碰撞概率和穿透概率的物理模型。
具体实施方式
[0050]
如前所述，下面给出一种基于经典基体弦长概率分布函数的计算示例。图1示出了其总体计算流程。图2则示出了基体1和其中的两个颗粒2，其中的颗粒k详细示出了层结构。图中的f(l0)为基体弦长概率分布函数，p0为中子在基体中的首次碰撞概率，t
k
为中子穿透基体后进入第k种颗粒的概率，p
k,i
为中子在第k种颗粒第i层的首次碰撞概率，p为总穿透概率。
[0051]
(1)首先，建立基于基体弦长概率分布函数的等效均匀化模型，其中，基体弦长概率分布函数为：
[0052][0053]
其中，为基体平均弦长：
[0054][0055]
其中，f
k
为第k种颗粒的体积填充率，r
k
为第k种颗粒的颗粒半径。
[0056]
(2)由基体弦长概率分布函数，计算中子在基体中的穿透概率e0和中子在基体中的首次碰撞概率p0：
[0057][0058][0059]
其中σ0为基体总截面。
[0060]
(3)计算中子穿透基体后进入第k种颗粒的概率t
k
：
[0061][0062]
其中，f
k
为颗粒体积份额，r
k
为颗粒半径。
[0063]
(4)通过一维球碰撞概率法，或通过构造“平行中子束穿过颗粒”的几何模型，计算中子进入第k种颗粒后在颗粒第i层发生首次碰撞的概率
[0064]
(5)计算中子在第k种颗粒第i层的首次碰撞概率p
k,i
：
[0065][0066]
(6)计算总穿透概率p：
[0067][0068]
(7)计算等效均匀化后的总穿透概率
[0069]
假设待求的等效均匀化总截面为用该截面填充基体和所有颗粒。
[0070]
中子在基体中的穿透概率为：
[0071][0072]
中子在均匀化颗粒k的穿透概率为：
[0073][0074]
其中是第k种颗粒的弦长概率分布函数。
[0075]
总穿透概率：
[0076][0077]
(8)计算等效均匀化总截面
[0078]
根据总穿透概率不变的原则，即得到关于的非线性方程：
[0079][0080]
构建以下迭代形式，通过数值算法计算等效均匀化总截面构建以下迭代形式，通过数值算法计算等效均匀化总截面
[0081]
(9)计算自屏因子s
k,j
，s0和等效均匀化截面
[0082]
首先计算各子区的有效截面：
[0083][0084]
[0085]
然后计算各子区的自屏因子：
[0086][0087][0088]
最后计算各反应类型的等效均匀化截面：
[0089][0090]
其中，下标k表示颗粒种类编号，j表示颗粒内的物质子区的编号，x表示反应类型编号；f
k,j
表示第k种颗粒、第j区占整个随机介质的体积份额，s
k,j
和σ
k,j,x
分别表示第k种颗粒、第j区的自屏因子和反应截面，s0和σ0分别表示基体的自屏因子和反应截面。
[0091]
以上记载了本发明的优选实施例，但是本发明的精神和范围不限于这里所公开的具体内容。本领域技术人员能够根据本发明的教导而做出更多的实施方式和应用，包括对上述实施例的各个技术特征的任意组合。这些实施方式和应用都在本发明的精神和范围内。本发明的精神和范围不由具体实施例来限定，而由权利要求来限定。