一种考虑装配误差与制造误差的齿轮传动误差方法

1.本发明属于齿轮传动误差预测技术领域，具体涉及一种考虑装配误差与制造误差的齿轮传动误差模型。


背景技术：

2.齿轮传动机构是精密传动机械中至关重要的传动形式之一，精密机械对传动精度要求较高，而齿轮误差直接影响到运动传递的准确性，因此人们针对齿轮传动误差开展了大量研究，分析误差来源，总结误差作用方式，建立了相应的检测标准。但现有的传动误差计算方法往往只关注于齿轮自身制造误差，而忽略掉齿轮装配过程中产生的装配误差，装配误差会影响齿轮的轴线位姿，从而对传动造成影响，因此建立齿轮实际轴线位姿变动矩阵，将传动误差分解为齿轮轴线位姿误差与齿轮自身误差分别进行求解在耦合，建立更为精确的传动误差模型。


技术实现要素：

3.有鉴于此，本发明提供一种考虑装配误差与制造误差的齿轮传动误差模型，能够将装配误差与制造误差综合考虑，计算得到传动误差。
4.本发明技术方案如下：
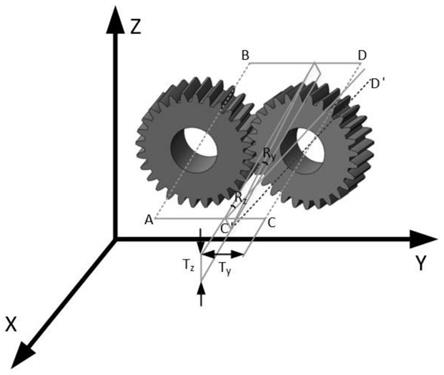
5.一种考虑装配误差与制造误差的齿轮传动误差模型，其特征在于，根据齿轮副误差特点，采用sdt方法构建齿轮副误差模型轴线ab与轴线cd为理想情况下齿轮副两啮合齿轮轴线位置，轴线c'd'为齿轮实际情况下引入误差后的轴线位置，轴线c'd'可以看作以轴线cd为基准沿y轴方向偏移距离t
y
,沿z轴方向偏移t
z
,,绕y轴方向旋转r
y
，绕z轴方向旋转r
z
。齿轮实际轴线c'd'的sdt非零向量为v＝(0,v,ω,0,β,γ)，则其sdt表达式为v＝(0,t
y
,t
z
,0,r
y
,r
z
)。因此，齿轮实际情况下轴线位姿可以表示为：
6.其中，矩阵l
the
、l
act
分别代表理论与实际轴线中各点的坐标，矩阵r、t分别代表实际轴线坐标系绕理论轴线坐标系坐标轴旋转与平移的位姿变换矩阵。由于轴线的误差转动分量微小，因此可以近似sinθ＝θ,cosθ＝1，并忽略计算过程中的高阶误差项，如sinr
·
t，则实际轴线坐标系相对于理想轴线坐标系的误差变动矩阵w
err
可以简化为：
7.建立齿轮齿距误差、径向跳动误差以及平行度误差与传动误差间函数关系。
8.根据所述的实际轴线坐标系相对于理想轴线坐标系的误差变动矩阵w
err
建立装配误差与传动误差间函数关系，具体的，误差变动矩阵中t
y
为沿y轴偏移量，对于正方向旋转主动齿轮，当t
y
值为正时，可以看作两工作齿面间隙减小，即圆周侧隙减小t
y
，对传动系统产生的误差大小可由下式计算：
9.误差变动矩阵中t
z
为沿z轴偏移量，对于正方向旋转主动齿轮，当t
z
值为正时，可以看作两工作齿轮间距减小，即径向侧隙减小t
z
，对传动系统产生的误差大小可由下式计算：
10.式中：r为分度圆半径(mm)，a
n
为分度圆法向齿形角(
°
)。
11.实际齿轮轴线坐标系由理想坐标系经过平移与旋转得到，在齿轮轴线平行度误差中将公共平面定义为一对啮合齿轮中两轴承跨距中较长的一个和另一根轴上的一个轴承来确定的平面，不考虑由于齿轮轴线坐标系平移变化对公共平面的影响，则误差变动矩阵中旋转角度值r
y
、r
z
可分别对应齿轮轴线平行度误差中在公共平面上的偏差以及与公共平面相垂直的交错轴平面上的偏差，因此，误差变动矩阵中旋转量对传动系统产生误差大小可由下式计算：可由下式计算：
12.单个齿距误差指实际齿距与理论齿距的代数差，齿距累积总偏差可反映齿轮一转过程中传动比的变化，是齿轮误差中的切向偏差，将齿距线性误差转化为齿轮分度圆处的角误差，则单个齿距误差所产生的角误差可由下式计算：
13.式中，为齿距产生的角误差(
°
)，f
pt
为齿距偏差(μm)，r为分度圆半径(mm)。
14.齿轮的径向跳动指从侧头到齿轮轴线的最大和最小径向距离之差，径向跳动会影响齿轮传递运动的准确性，是齿轮误差中的径向偏差，引起的径向侧隙转化为圆周侧隙并转化为分度圆处角误差，则齿轮径向跳动所产生的角误差可由下式计算：
15.式中，为径向跳动产生的角误差(
°
)，f
r
为径向跳动(μm)，r为分度圆半径(mm)，
16.两啮合齿轮的轴线平行度误差会造成啮合齿轮圆周方向的间隙，平行度误差可以分解为在公共平面上的偏差δf
y
以及与公共平面相垂直的交错轴平面上的偏差δf
x
，公共平面上轴线偏差δf
y
所引起的齿轮径向间隙，为齿轮轴线夹角，oo
‘
为齿轮轴线，选择中点a作为旋转不动点，b为齿宽，r为齿轮分度圆半径，可得出由于轴线偏差δf
y
所造成的齿
轮端面处最大径向位移量δf
j
：：齿轮轴线夹角由齿轮径向侧隙与圆周侧隙的关系可得圆周侧隙值由齿轮径向侧隙与圆周侧隙的关系可得圆周侧隙值则齿轮轴线平行度误差在公共平面内偏差引起的角误差为：
17.交错轴平面上轴线偏差δf
x
所造成的轮齿侧面变化量δf
c
：此变化量会造成齿轮啮合间隙减小，且则圆周侧隙值则圆周侧隙值则齿轮轴线平行度误差在交错轴平面内偏差引起的角误差为：
18.传动系统传动误差可由下式计算：
19.本发明的优点：本发明结合齿轮误差测量中齿距误差、齿轮径向跳动误差以及齿轮轴线平行度误差概念，将齿轮传动误差分解为齿轮轴线的位姿误差与齿轮制造误差，将轴线位姿误差变动矩阵中的各量值与传动误差建立函数关系，构建包含齿轮自身制造误差以及装配过程中对轴线位姿产生的误差变动的传动误差模型，可有效提高传动误差模型的准确性为实现传动误差预测提供基础。
附图说明：
20.图1为齿轮副误差模型示意图
21.图2为齿轮平行度误差示意图
22.图3为齿轮平行度误差在公共平面内偏差示意图
23.图4为齿轮平行度误差在交错轴平面内偏差示意图
24.图5为齿轮旋转正方向坐标系示意图
具体实施方式
25.下面结合附图对本发明进行详细描述
26.根据齿轮副误差特点，采用sdt方法构建齿轮副误差模型如图1，轴线ab与轴线cd为理想情况下齿轮副两啮合齿轮轴线位置，轴线c'd'为齿轮实际情况下引入误差后的轴线位置，轴线c'd'可以看作以轴线cd为基准沿y轴方向偏移距离t
y
,沿z轴方向偏移t
z
,,绕y轴方向旋转r
y
，绕z轴方向旋转r
z
。齿轮实际轴线c'd'的sdt非零向量为v＝(0,v,ω,0,β,γ)，
则其sdt表达式为v＝(0,t
y
,t
z
,0,r
y
,r
z
)。因此，齿轮实际情况下轴线位姿可以表示为：
27.其中，矩阵l
the
、l
act
分别代表理论与实际轴线中各点的坐标，矩阵r、t分别代表实际轴线坐标系绕理论轴线坐标系坐标轴旋转与平移的位姿变换矩阵。由于轴线的误差转动分量微小，因此可以近似sinθ＝θ,cosθ＝1，并忽略计算过程中的高阶误差项，如sinr
·
t，则实际轴线坐标系相对于理想轴线坐标系的误差变动矩阵w
err
可以简化为：
28.建立齿轮齿距误差、径向跳动误差以及平行度误差与传动误差间函数关系。
29.确立齿轮旋转方向，若齿轮旋转方向与轴线坐标系正方向满足右手螺旋定则，即大拇指指向与坐标系正方向一致，且齿轮旋转方向与四指方向一致，则将此时齿轮旋转方向称为正方向，反之则称为反方向。如图5所示，大拇指指向与x轴正方向一致，且齿轮旋转方向为正方向。
30.根据所述的实际轴线坐标系相对于理想轴线坐标系的误差变动矩阵w
err
建立装配误差与传动误差间函数关系，具体的，误差变动矩阵中t
y
为沿y轴偏移量，对于正方向旋转主动齿轮，当t
y
值为正时，可以看作两工作齿面间隙减小，即圆周侧隙减小t
y
，对传动系统产生的误差大小可由下式计算：
31.误差变动矩阵中t
z
为沿z轴偏移量，对于正方向旋转主动齿轮，当t
z
值为正时，可以看作两工作齿轮间距减小，即径向侧隙减小t
z
，对传动系统产生的误差大小可由下式计算：
32.式中：r为分度圆半径(mm)，a
n
为分度圆法向齿形角(
°
)。
33.实际齿轮轴线坐标系由理想坐标系经过平移与旋转得到，在齿轮轴线平行度误差中将公共平面定义为一对啮合齿轮中两轴承跨距中较长的一个和另一根轴上的一个轴承来确定的平面，不考虑由于齿轮轴线坐标系平移变化对公共平面的影响，则误差变动矩阵中旋转角度值r
y
、r
z
可分别对应齿轮轴线平行度误差中在公共平面上的偏差以及与公共平面相垂直的交错轴平面上的偏差，因此，误差变动矩阵中旋转量对传动系统产生误差大小可由下式计算：
34.单个齿距误差指实际齿距与理论齿距的代数差，齿距累积总偏差可反映齿轮一转过程中传动比的变化，是齿轮误差中的切向偏差，将齿距线性误差转化为齿轮分度圆处的角误差，则单个齿距误差所产生的角误差可由下式计算：
35.式中，为齿距产生的角误差(
°
)，f
pt
为齿距偏差(μm)，r为分度圆半径(mm)。
36.齿轮的径向跳动指从侧头到齿轮轴线的最大和最小径向距离之差，径向跳动会影响齿轮传递运动的准确性，是齿轮误差中的径向偏差，引起的径向侧隙转化为圆周侧隙并转化为分度圆处角误差，则齿轮径向跳动所产生的角误差可由下式计算：
37.式中，为径向跳动产生的角误差(
°
)，f
r
为径向跳动(μm)，r为分度圆半径(mm)，[0038]两啮合齿轮的轴线平行度误差会造成啮合齿轮圆周方向的间隙，平行度误差可以分解为在公共平面上的偏差δf
y
以及与公共平面相垂直的交错轴平面上的偏差δf
x
，如图2所示。公共平面上轴线偏差δf
y
所引起的齿轮径向间隙如图3所示，为齿轮轴线夹角，oo
‘
为齿轮轴线，选择中点a作为旋转不动点，b为齿宽，r为齿轮分度圆半径，可得出由于轴线偏差δf
y
所造成的齿轮端面处最大径向位移量δf
j
：：齿轮轴线夹角由齿轮径向侧隙与圆周侧隙的关系可得圆周侧隙值由齿轮径向侧隙与圆周侧隙的关系可得圆周侧隙值则齿轮轴线平行度误差在公共平面内偏差引起的角误差为：
[0039]
交错轴平面上轴线偏差δf
x
所造成的轮齿侧面变化量δf
c
如图4所示：此变化量会造成齿轮啮合间隙减小，且则圆周侧隙值则圆周侧隙值则齿轮轴线平行度误差在交错轴平面内偏差引起的角误差为：
[0040]
传动系统传动误差可由下式计算：
[0041]
本发明的优点：本发明结合齿轮误差测量中齿距误差、齿轮径向跳动误差以及齿轮轴线平行度误差概念，将齿轮传动误差分解为齿轮轴线的位姿误差与齿轮制造误差，将轴线位姿误差变动矩阵中的各量值与传动误差建立函数关系，构建包含齿轮自身制造误差以及装配过程中对轴线位姿产生的误差变动的传动误差模型，可有效提高传动误差模型的准确性为实现传动误差预测提供基础。