平面曲边多边形弹性包络线计算方法

1.本发明是一种平面曲边多边形弹性包络线计算方法，用于计算包含平面曲边多边形集合的最小凸集，属于计算几何中凸包求解领域。


背景技术：

2.平面几何对象的凸包求取是计算几何的基本问题之一，亦是被国内外学者密切关注的研究热点，现代工业和信息技术中的诸多领域均有涉及，例如碰撞检波、治金术、球粒人造多孔介质模型和点定位、图像处理、计算机辅助设计等皆可归结为此类问题。按照研究对象的不同，又可细分为针对点集、简单多边形、曲边多边形的凸包等几类。其中针对点集的凸包，有著名的graham扫描算法、jarvis“包扎”算法等；针对多边形的凸包，有mccallum算法、melkman算法、d.t.lee算法等；至于二维平面的曲边多边形，当前的相关研究还较为薄弱。鉴于曲边多边形的弹性包络线求解对于理论前沿攻克和工业生产实践的重要价值，研究平面曲边多边形弹性包络线计算方法，对于推动相关领域的前沿技术进步与交叉融合发展具有积极意义。


技术实现要素：

3.为了解决上述存在的技术问题，本发明提供一种平面曲边多边形弹性包络线的计算方法，该方法可自动完成平面上含有圆弧线、样条曲线等曲线边的多边形的弹性包络线的计算及输出，从而解决曲边形的凸包计算问题。
4.本发明的目的是通过下述技术方案实现的：
5.平面曲边多边形弹性包络线计算方法，该方法实现的主要步骤有：1)平衡判断。根据三个点的位置判断包络线在中间点处是否受力平衡。2)前进。当支点为平衡支点时将该点加入有序的平衡支点集合，并判断算法是否可继续向前推进，更新前进后的点。3)交叉判断。判断直线段是否与多边形交叉。4)回弹。当三点不平衡时向平衡支点回弹。5)跳跃。根据交叉点类型判断前进跳跃方式，并进行跳跃以此简化算法。6)求解包络线。求出所有平衡支点集后构造包络线的有序点集和有序边集。
6.所述步骤1)平衡判断，即通过物理模型判断以u点为起点，经过点v到达终点w的弹性线是否在v点受力平衡，将点v分为平衡支点和不平衡支点。
7.所述步骤2)前进，包含(1)前进判断；(2)添加支点。
8.所述(1)前进判断，即对当前点w根据简单闭多边形p及已经求得的有序点集q，将其分为可前进点并求出下一点w
new
和不可前进点。
9.所述简单闭多边形p，是根据定义1多边形定义，结合定义2闭多边形定义和定义3简单多边形定义的简单闭多边形。其顶点序列记为v(v0,v1,
…
,v
n
‑1)，其中v0≠v
n
‑1，即v0与v
n
‑1不重合，为边e
n
‑1的两个端点；边序列记为e＝(e0,e1,
…
,e
n
‑1)。
10.所述定义1，多边形定义如下：设v＝(v0,v1,
…
,v
n
)为欧氏空间r2中的一个点序列，v
i
和v
i+1
(i＝0,1,
…
,n
‑
1)间均定义了唯一一条边亦即前者为e
i
的两个端点，e＝
(e0,e1,
…
,e
n
‑1)为e
i
(i＝0,1,
…
,n
‑
1)构成的一个与v相关的序列，则称e为一个多边形p，记为p＝(v,e)，称v
i
(i＝0,1,
…
,n)为p的顶点。
11.所述定义2，闭多边形定义如下：若v0＝v
n
，则称p为闭多边形。
12.所述定义3，简单多边形定义如下：若p满足下列条件：对任意i,j＝0,1,
…
,n，i≠j，除v0＝v
n
可成立外，v
i
≠v
j
；对任意i＝0,1,
…
,n
‑
2，k＝2,3,
…
,n
‑
1，i+k≤n
‑
1，除外，e
i
∩e
i+1
＝v
i+1
，则称p为简单多边形。
13.所述(2)添加支点，即当从u经过点v到w点的弹性线在v点平衡且w点为可前进点时，将点v加入有序点集q中，并根据w
new
生成新的u、v、w三点。
14.所述步骤3)交叉判断，即当从u经过点v到w点的弹性线在v点不平衡时，判断直线段是否与多边形p交叉，包括(1)线段与边间关系判断；(2)线段与多边形关系判断。
15.所述(1)线段与边间关系判断，即判断直线段与p的每条边之间的关系。
16.所述(2)线段与多边形关系判断，即依据线段与边间关系的判断结果将与p的关系分为与p有交叉，与p仅接触，与p相离，并求出叉点集或触点集。
17.所述步骤4)回弹，即当从u经过点v到w点的弹性线在v点不平衡且与p相离时，将点v舍弃并向前一平衡支点回弹，根据有序点集q生成新的u、v、w三点及q。
18.所述步骤5)跳跃，包括(1)跳跃判断；(2)前跳跃；(3)后跳跃；(4)前后跳跃。
19.所述(1)跳跃判断，即当从u经过点v到w点的弹性线在v点不平衡且与p不相离时，求出退后点w
′
和触点集t并确定跳跃类型为前跳跃、后跳跃还是前后跳跃。
20.所述(2)前跳跃，即根据w
′
点、触点集t，使现有支点向前跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，通过本方法求解p
′
的弹性包络线，来直接得到p的弹性包络线p
ch
或更新u、v、w三点。
21.所述(3)后跳跃，即根据w
′
点、触点集t，使现有支点向后跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，通过本方法求解p
′
的弹性包络线，来直接得到p的弹性包络线p
ch
或更新u、v、w三点。
22.所述(4)前后跳跃，即根据w
′
点、触点集t，使现有支点向前向后跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，通过本方法求解p
′
的弹性包络线，来直接得到p的弹性包络线p
ch
或更新u、v、w三点。
23.所述步骤6)求解包络线，包括(1)生成边；(2)生成包络线。
24.所述(1)生成边，即当所有平衡支点都加入有序点集q中时(出现不可前进点时)，根据有序点集q，求出弹性包络线有序点集v
ch
和有序边集e
ch
。
25.所述(2)生成包络线，即根据弹性包络线的有序点集v
ch
和有序边集e
ch
构造弹性包络线p
ch
。
26.应用本发明的有益效果如下：平面曲边多边形弹性包络线计算方法创造性地将数学模型转化为物理模型，从而可简单快速地计算出弹性包络线关键顶点；该方法不仅可精确计算平面多边形的凸包，并可计算平面曲边多边形的弹性包络线，具有一定的通用性；经测试，平面曲边多边形弹性包络线计算方法能在可接受时间范围内获取质量较优的运算结果，且结果的稳定性较好，鲁棒性较优。
附图说明
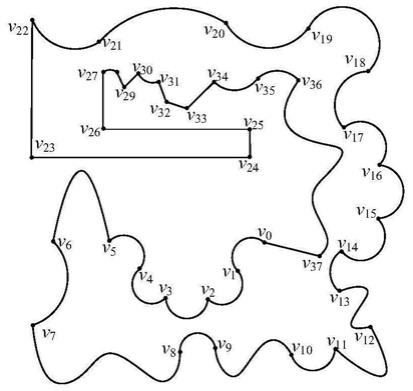
27.图1为含有曲边的简单闭多边形示意图。
28.图2为平面曲边多边形弹性包络线计算方法总流程图。
29.图3为v点受力示意图。
30.图4为回弹示意图。
31.图5为多边形前跳跃示意图。
32.图6为多边形后跳跃示意图。
33.图7为生成边示意图。
34.图8为多边形弹性包络线示意图。
具体实施方式
35.下面结合附图对本发明的实施实例进行详细说明，该实例以发明技术方案为前提进行，本发明给出了详细的实施方式和具体的实现过程，但是本发明的保护范围不限于下述实施实例。
36.下面将结合附图对发明进行进一步的详细说明，如附图1所示为本发明的实施例对象，含有圆弧、样条曲线等曲线边的多边形p＝(v,e)，其中v＝(v0,v1,
…
,v
37
)，e＝(e0,e1,
…
,e
37
)；如附图2所示为本发明实施例所述的平面曲边多边形弹性包络线计算方法流程图。
37.该方法实现的总流程为：1)平衡判断，2)前进，3)交叉判断，4)回弹，5)跳跃，6)生成边。
38.首先做好计算前准备工作，获取简单闭多边形的顶点及边，并从起始点v0开始，获得初始的u、v、w三点。
39.步骤1)：平衡判断
40.通过物理模型判断以u点为起点，经过点v到达终点w的弹性线是否在v点受力平衡。图3为v点受力示意图，设v为均匀轻质弹性线l中的一个点，u、w分别为弹性线l上位于点v前后两侧的始末点。f1和f2为u和w点对弹性线的拉力，f
n
为v处所受的支撑力。若f1+f2+f
n
＝0，则弹性线在支点v点受力平衡。
41.步骤2)前进
42.(1)前进判断
43.对当前点w根据p及有序点集q，判断其是否可以继续前进并求出前进点w
new
。
44.(2)添加支点。
45.当从u经过点v到w点的弹性线在v点平衡且w点为可前进点时，将点v加入有序点集q中，并根据w
new
更新u、v、w三点。
46.步骤3)交叉判断
47.(1)线段与边间关系判断
48.根据直线段与p的边e(v
s
,v
e
)的交点数量及交点与u、v、v
s
、v
e
的关系，判断直线段与e之间的关系。
49.(2)线段与多边形关系判断。
50.基于线段与边间关系的判断结果，将与p的关系分为与p有交叉，与p仅接
触，与p相离，并求出叉点集或触点集。
51.步骤4)回弹
52.当从u经过点v到w点的弹性线在v点不平衡且与p相离时，将点v舍弃并向前一平衡支点回弹。图4为回弹示意图。图中u经过点v到w点的弹性线在v点不平衡，前一平衡支点为u点，进行回弹并根据有序点集q更新u＝q、v＝u、w不变，然后更新有序点集q。
53.步骤5)跳跃
54.(1)跳跃判断
55.当从u经过点v到w点的弹性线在v点不平衡且与p不相离时，求出退后点w
′
和触点集t并确定跳跃类型为前跳跃、后跳跃还是前后跳跃。
56.(2)前跳跃
57.根据w
′
点、触点集t，使现有支点向前跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，图5为多边形p前跳跃示意图。示意图中w所在边为e
36
，触点所在边为e5，经过跳跃判断判断为前跳跃。求得新的简单闭多边形p
′
，图示为红色顶点和边组成的多边形。该图中p
′
的弹性包络线不存在，所以根据跳跃点w
jump
进行跳跃并更新u、v、w三点。若p
′
的弹性包络线存在，则p
′
的弹性包络线即为p的弹性包络线p
ch
。
58.(3)后跳跃
59.根据w
′
点、触点集t，使现有支点向后跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，图6为多边形p后跳跃示意图。示意图中w所在边为e
26
，触点所在边为e
29
、e
32
、e
33
，经过跳跃判断判断为后跳跃。求得新的简单闭多边形p
′
，图示为红色顶点和边组成的多边形。该图中p
′
的弹性包络线不存在，所以根据跳跃点w
jump
进行跳跃并更新u、v、w三点。若p
′
的弹性包络线存在，则p
′
的弹性包络线即为p的弹性包络线p
ch
。
60.(4)前后跳跃。
61.根据w
′
点、触点集t，使现有支点进行前后跳跃，获得跳跃点w
jump
和新的简单闭多边形p
′
，若p
′
的弹性包络线不存在，根据跳跃点w
jump
进行跳跃并更新u、v、w三点。若p
′
的弹性包络线存在，则p
′
的弹性包络线即为p的弹性包络线p
ch
。
62.步骤6)求解包络线
63.(1)生成边
64.当所有平衡支点都加入有序点集q中时(出现不可前进点时)，根据有序点集q，求出弹性包络线有序点集v
ch
和有序边集e
ch
。图7为生成边示意图，有序点集q中的点(q
i
,q
i+1
,
…
,q
i+n
)求得的弹性包络线的边为将顶点和加入v
ch
，加入e
ch
。
65.(2)生成包络线。
66.根据弹性包络线的有序点集v
ch
和有序边集e
ch
构造弹性包络线p
ch
。图8为多边形p的弹性包络线示意图。
67.以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明披露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。