运算控制方法、装置、系统、存储介质及处理器与流程

1.本发明涉及数据处理技术领域，具体涉及一种运算控制方法、装置、系统、存储介质及处理器。


背景技术：

2.随着人工智能的发展，神经网络的应用已经深入生活的各个部分。常用的神经网络都需要极大数量的乘、加运算，例如深度神经网络(deep neural networks，dnn)、卷积神经网络(convolutional neural networks，cnn)等。现有的通用处理器已经无法承受，设计专门进行网络运算的嵌入式神经网络处理器(neural network processing units，npu)成为主流。而大规模的乘法器阵列是npu中主要的运算单元。
3.目前，对有符号高位宽的操作数执行乘法操作的方法，复杂度较高，不适合在类似npu这样的大规模乘法器阵列上使用。


技术实现要素：

4.本发明要解决的问题是：降低对有符号高位宽的操作数执行乘法操作的复杂度。
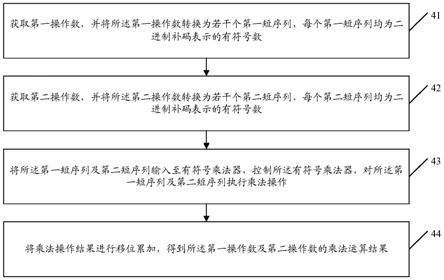
5.为解决上述问题，本发明实施例提供了一种运算控制方法，所述方法包括：获取第一操作数，并将所述第一操作数转换为若干个第一短序列，每个第一短序列均为二进制补码表示的有符号数；获取第二操作数，并将所述第二操作数转换为若干个第二短序列，每个第二短序列均为二进制补码表示的有符号数；将所述第一短序列及第二短序列输入至有符号乘法器，控制所述有符号乘法器，对所述第一短序列及第二短序列执行乘法操作；将乘法操作结果进行移位累加，得到所述第一操作数及第二操作数的乘法运算结果；其中，所述第二短序列的个数与所述第一短序列的个数相同；所述第一短序列及第二短序列的位宽与所述有符号乘法器的输入位宽相同；所述有符号乘法器的个数，大于或等于所述第一短序列个数第二短序列个数的乘积。
6.本发明实施例还提供了一种运算控制装置，所述装置包括：第一转换单元，适于获取第一操作数，并将所述第一操作数转换为若干个第一短序列，每个第一短序列均为二进制补码表示的有符号数；第二转换单元，适于获取第二操作数，并将所述第二操作数转换为若干个第二短序列，每个第二短序列均为二进制补码表示的有符号数；运算控制单元，适于将所述第一短序列及第二短序列输入至有符号乘法器，控制所述有符号乘法器，对所述第一短序列及第二短序列执行乘法操作；移位累加单元，适于将乘法操作结果进行移位累加，得到所述第一操作数及第二操作数的乘法运算结果；其中，所述第二短序列的个数与所述第一短序列的个数相同；所述第一短序列及第二短序列的位宽与所述有符号乘法器的输入位宽相同；所述有符号乘法器的个数，大于或等于所述第一短序列个数与第二短序列个数的乘积。
7.本发明实施例还提供了一种运算控制系统，所述系统包括：上述实施例中的运算控制装置；及若干个有符号乘法器；其中，所述运算控制装置与所述有符号乘法器连接；所
述有符号乘法器适于在所述运算控制装置的控制下执行乘法操作；所述有符号乘法器的个数，大于或等于所述运算控制装置中第一短序列个数与第二短序列个数的乘积。
8.本发明实施例还提供了一种处理器，所述处理器包括上述实施例中的运算控制系统。
9.本发明实施例还提供了一种计算机存储介质，所述计算机存储介质上存储有计算机程序，所述计算机程序被处理器执行，以实现上述运算控制方法的步骤。
10.与现有技术相比，本发明实施例的技术方案具有以下优点：
11.应用本发明的方案，通过将第一操作数转换为若干个第一短序列，将第二操作数转换为若干个第二短序列，由于所述第一短序列及第二短序列均为二进制补码表示的有符号数，故可以统一采用有符号乘法器对第一短序列及第二短序列执行乘法操作，避免了有符号数与无符号数间的复杂转换，降低运算控制复杂度。另外，采用本发明的方案，由于所述第一短序列及第二短序列的长度与所述有符号乘法器的位宽相同，故无论输入操作数的位宽如何，均可以统一转换成与有符号乘法器位宽相同的短序列，并执行相应的乘法操作，无需根据不同的操作数位宽进行单独的运算控制，进一步降低运算控制复杂度，更适合使用在类似npu这样的大规模乘法器阵列上。
附图说明
12.图1是采用非直接拆分法进行m比特的有符号乘法的过程示意图；
13.图2是采用非直接拆分法进行2m比特的有符号乘法的过程示意图；
14.图3是采用非直接拆分法进行4m比特的有符号乘法的过程示意图；
15.图4是本发明实施例中一种运算控制方法的流程图；
16.图5是本发明实施例中一种对第一输入序列及第二输入序列执行乘法操作的示意图；
17.图6是本发明实施例中乘法运算的过程示意图；
18.图7是本发明实施例中一种运算控制装置的结构示意图；
19.图8是本发明实施例中一种运算控制系统的结构示意图。
具体实施方式
20.目前，对有符号高位宽的操作数执行乘法操作时，可以直接调用电子设计自动化(electronics design automation，eda)工具或者制造(fabrication，fab)厂设计库中的乘法器模型来实现。
21.上述方案虽然最为直接，但直接使用高位宽的乘法器时，即便经过了eda或fab厂商的优化，仍然面积巨大，而且时序很差，通常难以运行在200mhz以上频率的时钟。并且，实例化一个高位宽的乘法器不能等效为多个低位宽的乘法器，例如一个32比特的乘法器只能实现一个16位的乘法，尽管输入的操作数的位宽只有一半，这样在操作数具有不同位宽运算的场景，此方法极为不灵活，一般设计都不采用。
22.另一种对有符号高位宽的操作数执行乘法操作的方案，是将输入的操作数进行直接拆分。具体地，将输入的有符号操作数，直接拆分为若干较短的序列，然后将较短的序列进行乘法运算，再将积进行合适的移位和相加得到原数据乘法的结果。
23.例如，输入的操作数分别为x和y，其中，对操作数x直接拆分后，x可以表示为：
24.x＝p
k
‑1p
k
‑2...p1p0ꢀꢀꢀ
(1)
25.其中，k是拆分的序列数。对于任一短序列p
i
＝a
m(i+1)
‑1...a
mi
，k
‑
1≥i≥0，m是短序列p
i
的比特数。例如，x是32位有符号数，选择k＝4，m＝8，则将32位序列拆分为4个8位的序列。
26.同理，对操作数y直接拆分后，y可以表示为：
27.y＝q
k
‑1q
k
‑2...q1q0ꢀꢀꢀ
(2)
28.其中，对于y拆分后的任意短序列q
j
＝b
m(j+1)
‑1...b
mj
，k
‑
1≥j≥0
29.最终，对于x和y执行乘法操作时，可以使用k2个m比特的乘法器来实现如下：
[0030][0031]
在直接拆分法中，对于操作数x，其拆分结果中，短序列p
k
‑1是二进制补码表示的有符号数，其他均为二进制无符号数。对于操作数y，其拆分结果中，短序列q
k
‑1是二进制补码表示的有符号数，其他均为二进制无符号数。
[0032]
采用乘法器实现公式(3)时，短序列p
k
‑1及q
k
‑1参与的乘法操作均为有符号乘法操作或是有符号乘以无符号的乘法操作，其它短序列参与的乘法操作均为m比特的无符号乘法操作。有符号乘法操作需要使用有符号的乘法器，而无符号的乘法操作需要使用无符号的乘法器，故共需要1个有符号乘法器，2k
‑
2个有符号乘以无符号的乘法器，以及(k
‑
1)2个无符号乘法器。其中，2k
‑
2个有符号乘以无符号的乘法器，一般需要位宽(m+1)比特的有符号乘法器来实现。
[0033]
在直接拆分法中，由于所使用的乘法器类型包括多种，乘法器的类型不统一，使得乘法器在规模阵列的设计中会非常复杂。并且，用该方法来等效的低位宽的乘法器(比如m比特的乘法器)其类型也很难确定，更不用提如何能等效2m比特、4m比特的乘法器这些更为灵活的用法了。
[0034]
还有一种对有符号高位宽的操作数执行乘法操作的方案，是将输入的操作数进行非直接拆分，并使用m比特无符号乘法器实现对拆分后序列的乘法操作。具体地，先将操作数x和y转换为无符号数，再进行拆分，使用无符号乘法器对拆分的短序列执行乘法操作后，再对操作结果进行符号转换。
[0035]
其中，无论是对高位宽的操作数直接执行乘法操作，还是对等效后的低位宽的操作数执行乘法操作，均需要先对其取绝对值，然后再执行后续的乘法操作及符号转换等步骤。具体对操作数取绝对值时，先记录下操作数的符号，再计算得到操作数的绝对值。
[0036]
例如，参照图1，假设操作数x等效后的低位宽的操作数包括x3、x2、x1及x0，x3、x2、x1及x0的位宽均为m比特，操作数y等效后的低位宽的操作数包括y3、y2、y1及y0，y3、y2、y1及y0的位宽也均为m比特。
[0037]
对操作数x等效后的低位宽的操作数执行乘法操作前，先记录x3、x2、x1及x0的符号依次为s3、s2、s1及s0，再对x3、x2、x1及x0取绝对值依次为|x3|、|x2|、|x1|及|x0|。同样地，对操作数y等效后的低位宽的操作数执行乘法操作前，先记录y3、y2、y1及y0的符号依次为r3、r2、r1及r0，再对y3、y2、y1及y0取绝对值依次为|y3|、|y2|、|y1|及|y0|。接着，对各个绝对值执行乘法操作，得到对应的结果|z3|、|z2|、|z1|及|z0|。最后利用之前记录的符号
位决定是否对乘法操作的结果取反。
[0038]
图2中与图1不同的是，操作数x等效后的低位宽的操作数仅包括x1及x0，操作数y等效后的低位宽的操作数仅包括y1及y0。其中，x0的位宽均为2m比特。y1及y0的位宽均为2m比特。
[0039]
具体执行乘法操作时，为了适配位宽为m比特的乘法器，将x0拆分为低m位|x0|
l
及高m位|x0|
h
，将x1拆分为低m位|x1|
l
及高m位|x1|
h
，将y0拆分为低m位|y0|
l
及高m位|y0|
h
，将x0拆分为低m位|y0|
l
及高m位|y1|
h
，得到乘法操作结果t0至t7后，先进行移位相加，再利用之前记录的符号位决定是否对移位相加的结果取反。
[0040]
图3与图2不同的是，操作数x等效后的低位宽的操作数仅包括x0，操作数y等效后的低位宽的操作数仅包括y0。其中，x0及y0的位宽均为4m比特。具体运算过程可以参照上述关于图2的描述，此处不再赘述。
[0041]
以x0为例，对操作数x0取绝对值时，如果x0本身为正数，为x0的绝对值仍为x0本身。若x0本身为负数，则需要对x0取相反数，即对x0先按位取反再加1，即|x0|＝～x0+1。在图1中，当x0位宽为m比特时，需要对该m比特取相反数，而在图2中，当x0位宽为2m比特时，需要对该2m比特取相反数，在图3中，当x0位宽为4m比特时，需要对该4m比特取反，由此可知，在使用非直接拆分法执行乘法操作时，需要根据输入操作数的长度不同要进行m/2m/4m三种类型的取反动作，不同类型的操作在电路实现上不能兼容，逻辑非常复杂。
[0042]
并且，在使用非直接拆分法执行乘法操作时，面对位宽不同的乘法也需要单独根据输入操作数的位宽不同，进行单独的运算控制，增加运算控制复杂度，不适合使用在类似npu这样的大规模乘法器阵列上。
[0043]
针对上述问题，本发明实施例提供了一种运算控制方法，应用所述方法，第一操作数对应的第一短序列，以及第二操作数对应的第二短序列，均为二进制补码表示的有符号数，故可以统一采用有符号乘法器对第一短序列及第二短序列执行乘法操作，避免了有符号数与无符号数间的复杂转换，降低运算控制复杂度。另外，由于所述第一短序列及第二短序列的长度与所述有符号乘法器的位宽相同，故无论输入操作数的位宽如何，均可以统一转换成与有符号乘法器位宽相同的短序列，并执行相应的乘法操作，进一步降低运算控制复杂度。
[0044]
为使本发明的上述目的、特征和优点能够更为明显易懂，下面结合附图对本发明的具体实施例作详细地说明。
[0045]
参照图4，本发明实施例提供了一种运算控制方法，所述方法可以包括如下步骤：
[0046]
步骤41，获取第一操作数，并将所述第一操作数转换为若干个第一短序列，每个第一短序列均为二进制补码表示的有符号数。
[0047]
在具体实施中，可以采用多种方式，获取第一操作数。比如，可以从指定存储器中读取第一操作数，或者外部直接输入第一操作数。
[0048]
在具体实施中，将第一操作数转换为若干个第一短序列，可以存在多种方法，只要由二进制补码表示的有符号数所构成的第一短序列，等于第一操作数的原值即可。
[0049]
所述第一操作数的位宽通常为有符号乘法器位宽的整数倍，比如，有符号乘法器的输入位宽为m比特时，所述第一操作数的位宽可以为km比特，k为≥1且k为整数。当然，在一些实施例中，所述第一操作数的位宽可以通过高位补符号位的方式，等效成有符号乘法
器的位宽的整数倍。
[0050]
在具体实施中，为了后续能够利用有符号乘法器对第一短序列执行乘法操作，所述第一短序列的位宽应与有符号乘法器的位宽相同。在存在多个有符号乘法器时，每个有符号乘法器的位宽可以相同，也可以不同，第一操作数对应的若干个第一短序列的位宽，与有符号乘法器的位宽相匹配。
[0051]
在本发明的一实施例中，将所述第一操作数转换为若干个第一短序列时，可以先按照所述有符号乘法器的位宽，将所述第一操作数拆分为若干个第一拆分序列，再依据当前第一拆分序列本身的二进制补码序列及后一第一拆分序列对应二进制补码序列的最高位的值，得到所述当前第一拆分序列对应的第一短序列。
[0052]
假设第一短序列的个数为k个，相应地，第一拆分序列的个数也为k个。p
i
表示第i+1个第一拆分短序列，i∈[0,k
‑
1]，则将第一操作数x拆分为若干个第一拆分序列，可以表示为：
[0053]
x＝p
k
‑1p
k
‑2...p1p0ꢀꢀꢀ
(4)
[0054]
其中，若当前第一拆分短序列为p
i
，则其后一第一拆分短序列为p
i
‑1。例如，第一拆分短序列p
k
‑1的后一第一拆分短序列为p
k
‑2，第一拆分短序列p
k
‑2的后一第一拆分短序列为p
k
‑3，
……
。
[0055]
当第一操作数x为有符号数时，第一操作数x对应的第一拆分序列可以包括：无符号序列，及包含所述第一操作数最高位且由二进制补码表示的有符号序列。比如，当第一操作数x为有符号数时，第一拆分序列p0至p
k
‑1中，第一拆分序列p0至p
k
‑2是无符号序列，p
k
‑1是有符号序列。并且，该有符号序列p
k
‑1已由二进制补码表示，即第一拆分序列p
k
‑1对应第一短序列为其本身。后续只要将无符号序列，转换为对应的第一短序列即可。
[0056]
若当前第一拆分短序列为p
i
，则其后一第一拆分短序列为p
i
‑1[0057]
假设每个有符号乘法器的位宽均相同且均为m比特。相应地，第一拆分序列位宽也均为m比特，则可以通过公式(5)，得到第一拆分短序列p
i
对应的二进制补码序列
[0058][0059]
从公式(5)可以看出，当第一拆分短序列p
i
的值(十进制)小于2
m
‑1时，第一拆分短序列p
i
对应的二进制补码序列，即第一拆分短序列p
i
本身。当第一拆分短序列p
i
的值大于或等于2
m
‑1时，第一拆分短序列p
i
对应的二进制补码序列
[0060]
假设c
i
为第一拆分序列的最高位的值，则可以依据公式(6)，得到第一操作数x对应的若干个第一短序列：
[0061][0062]
其中，为第一拆分序列p
k
‑1对应的第一短序列，为第一拆分序列p
k
‑2对应的第一短序列，为第一拆分序列p1对应的第一短序列，为第一拆分序列p0对应的第一短序列。
[0063]
例如，一个32bit的有符号数第一操作数x＝(8f927f81)
hex
，hex表示十六进制。第
一操作数x是一个负数。假设m＝8、k＝4，第一操作数x对应的第一拆分序列可以表示为：
[0064]
x＝(8f)
s
(92)
u
(7f)
u
(81)
u
＝(
‑
113)(146)(127)(129)
decimal
[0065]
其中，s表示为二进制补码，u表示为无符号，decimal表示十进制值。
[0066]
(8f)
s
、(92)
u
、(7f)
u
及(81)
u
为第一操作数对应的四个第一拆分序列。其中，第一拆分序列(8f)
s
已是二进制补码序列。故仅需确定(92)
u
、(7f)
u
及(81)
u
的二进制补码序列即可。第一拆分序列(8f)
s
的后一第一拆分序列为(92)
u
，第一拆分序列(92)
u
的后一第一拆分序列为(7f)
u
，第一拆分序列(7f)
u
的后一第一拆分序列为(81)
u
。
[0067]
根据公式(5)，可以得到第一拆分序列(92)
u
、(7f)
u
及(81)
u
对应的二进制补码序列依次为：
[0068]
(92)
u
＝(146)
dec
＝28+(92)
s
[0069]
(7f)
u
＝(7f)
s
[0070]
(81)
u
＝28+(81)
s
[0071]
第一拆分序列(92)
u
及(81)
u
的最高位的值为1，故为了保证x等于原值，则根据公式(6)，可以得到第一操作数x对应的第一短序列为：
[0072]
x＝(8f+1)
s
(92)
s
(7f+1)
s
(81)
s
[0073]
步骤42，获取第二操作数，并将所述第二操作数转换为若干个第二短序列，每个第二短序列均为二进制补码表示的有符号数。
[0074]
在具体实施中，可以采用多种方式，获取第二操作数。比如，可以从指定存储器中读取第二操作数，或者外部直接输入第二操作数。所述第二操作数的获取方式，可以与第一操作数的获取方式相同，也可以不同。
[0075]
在具体实施中，将第二操作数转换为若干个第二短序列，可以存在多种方法，只要由二进制补码表示的有符号数所构成的第二短序列，等于第二操作数的原值即可。所述第二短序列的个数，与所述第一短序列的个数相同。
[0076]
所述第二操作数的位宽通常为有符号乘法器位宽的整数倍。在一些实施例中，所述第二操作数的位宽可以通过高位补符号位的方式，等效成有符号乘法器的位宽的整数倍。所述第二操作数的位宽，可以与第一操作数的位宽相同，也可以与第一操作数的位宽不同，具体不作限制。
[0077]
比如，当第一操作数共对应5个第一短序列，其中三个第一短序列的位宽为2m比特，剩余两个第一短序列的位宽为3m比特。第二操作数共对应5个第二短序列，其中三个第二短序列的位宽为2m比特，剩余两个第二短序列的位宽为3m比特。此时，可以设置25个有符号乘法器，其中，25个有符号乘法器可以包括以下3种类型，分别为：1、2m*2m的乘法器，数量为3*3＝9个；2、3m*3m的乘法器，数量为2*2＝4个；3、2m*3m的乘法器，数量为2*3*2＝12个。
[0078]
在本发明的一实施例中，将所述第二操作数转换为若干个第二短序列时，可以先按照所述有符号乘法器的位宽，将所述第二操作数拆分为若干个第二拆分序列，再依据当前第二拆分序列本身的二进制补码序列及后一第二拆分序列对应二进制补码序列的最高位的值，得到所述当前第二拆分序列对应的第二短序列。
[0079]
假设第二短序列的个数为h个，相应地，第二拆分序列的个数也为h个。表示第j+1个第二拆分短序列，j∈[0，h
‑
1]，则将第二操作数y拆分为若干个第二拆分序列，可以表示为：
[0080]
y＝q
h
‑1q
j
‑2...q1q0；
ꢀꢀꢀ
(7)
[0081]
关于如何得到第二拆分序列对应的二进制补码序列，具体可以参照上述关于得到第一拆分序列p
i
对应的二进制补码序列的相关描述进行实施，此处不再赘述。
[0082]
在具体实施中，通过以下方法，将所述第二操作数y转换为若干个第二短序列：
[0083][0084]
其中，为第二拆分序列q
j
的二进制补码序列，w
j
为第二拆分序列q
j
的最高位的值，j∈[0，h
‑
1]，h为第二短序列的个数。具体可以参照上述关于得到第一拆分序列p
i
对应的第一短序列的相关描述进行实施，此处不再赘述。
[0085]
需要说明的是，在具体实施中，可以先执行步骤41，再执行步骤42，也可以先执行步骤42，再执行步骤41，还可以同时执行步骤41及步骤42，具体执行顺序不作限制。
[0086]
步骤43，将所述第一短序列及第二短序列输入至有符号乘法器，控制所述有符号乘法器，对所述第一短序列及第二短序列执行乘法操作。
[0087]
在本发明的实施例中，有符号乘法器，指的是能够对有符号数执行乘法操作的乘法器，即该乘法器的两输入端输入的数据均为有符号数，且输出结果也为有符号数。
[0088]
在本发明的实施例中，所设置的有符号乘法器的数量，应大于等于第一短序列个数与第二短序列个数的乘积。当有符号乘法器的数量大于第一短序列个数与第二短序列个数的乘积时，与第一短序列个数与第二短序列个数的乘积相等数量的有符号乘法器用于执行乘法操作，剩余有符号乘法器可以闲置或对其它操作数执行乘法操作。
[0089]
将所述第一短序列及第二短序列输入至有符号乘法器，此时，对于同一有符号乘法器的一输入端输入第一短序列，另一输入端输入第二短序列。可以向所述有符号乘法器发送触发信号，来触发有符号乘法器执行乘法操作。
[0090]
需要说明的是，在具体实施中，每个有符号乘法器的位宽可以均相同，也可以不同，具有与输入至该有符号乘法器的第一短序列及第二短序列的位宽相同即可。
[0091]
为了降低实现复杂度，在一实施例中，可以设置每个有符号乘法器的位宽均相同。相应地，设置每个第一短序列的位宽也相同，且等于有符号乘法器的位宽。比如，当第一短序列及第二短序列位宽均相同且均为m比特时，可以设置有符号乘法器的输入位宽为m*m比特。
[0092]
在采用非直接拆分法执行乘法操作时，由于m比特有符号数的表示范围为
‑2m
‑1～2
m
‑1‑
1，其绝对值的表示范围0～2
m
‑1，即使用m
‑
1比特来表示操作数的绝对值时，由于绝对值的比特数为m比特大于m
‑
1比特，故存在溢出问题。而用m bit来表示操作数的绝对值时，由于第m比特仅在操作数的绝对值为2
m
‑1时才会被利用，故又存在浪费问题。
[0093]
为此，为了避免溢出并减少浪费，在本发明的一实施例中，在得到第一短序列后，将所述第一短序列输入至有符号乘法器之前，可以依据后一第一拆分序列对应二进制补码序列的最高位的值，对当前第一短序列进行调整，得到当前第一短序列对应的第一输入序列，并将所述第一输入序列输入至有符号乘法器；所述当前第一短序列为当前第一拆分序列对应的第一短序列。
[0094]
具体当前第一短序列进行调整的方式不作限制。在本发明的一实施例中，可以在后一第一拆分序列对应二进制补码序列的最高位的值为1时，先对当前拆分序列对应的第
一短序列执行按位取反操作，再将所述按位取反操作后得到的二进制补码序列进行标记，得到当前第一拆分序列对应的标记后的二进制补码序列，并将所述标记后的二进制补码序列输入至有符号乘法器。在后一第一拆分序列对应二进制补码序列的最高位的值为0，则保持当前第一拆分序列对应的第一短序列输入至有符号乘法器。
[0095]
以第i个第一拆分序列p
i
为例，第一拆分序列p
i
对应的第一短序列为对应的第一短序列为考虑到第一短序列可能存在溢出，则可以根据如下公式，得到最终输入至有符号乘法器的第一输入序列s
i
：
[0096][0097]
也就是说，当第一拆分序列p
i
的后一第一拆分序列最高位的值c
i
‑1＝0时，第一输入序列此时，第一输入序列s
i
的值域范围为
‑2m
‑1～2
m
‑1‑
1。
[0098]
但当第一拆分序列p
i
的后一第一拆分序列最高位的值c
i
‑1＝1时，＝1时，＝1时，的值域范围为
‑2m
‑1+1～2
m
‑1，超过了位宽为m比特的有符号乘法器的表示范围，故可以使用的相反数来记录第一输入序列s
i
，使得第一输入序列s
i
的值域范围仍为
‑2m
‑1～2
m
‑1‑
1。
[0099]
由于而～表示按位取反，可以看到+1的过程恰好被
‑
1的过程抵消，的值就仅仅是的按位取反，避免了+1的复杂逻辑。
[0100]
以第一操作数x＝(8f927f81)
hex
为例进行说明，如上所述，第一操作数x对应的第一短序列为：
[0101]
x＝(8f+1)
s
(92)
s
(7f+1)
s
(81)
s
。
[0102]
由于第一短序列(7f+1)
s
出现了溢出现象，为了避免这个现象，可以将凡是存在+1这个操作的第一短序列在+1后再乘以
‑
1，以对该二进制补码序列进行标记。此时，(7f+1)
s
＝((7f+1)
·
(
‑
1))
s
·
(
‑
1)＝(80)
s
·
(
‑
1)，根据前面的推导(80)就是(7f)的按位取反，此处没有按位取反再加1的过程。此时可以得到第一操作数各第一短序列对应的第一输入序列，并得到第一操作数x的完整拆分结果：
[0103]
x＝8f927f81＝((70)
s
·
(
‑
1))(92)
s
((80)
·
(
‑
1))
s
(81)
s
。
[0104]
同理，在得到第二短序列后，将所述第二短序列输入至有符号乘法器之前，也可以依据后一第二拆分序列对应二进制补码序列的最高位的值，对当前第二短序列进行调整，得到当前第二短序列对应的第二输入序列，并将所述第二输入序列输入至有符号乘法器，所述当前第二短序列为当前第二拆分序列对应的第二短序列。具体对当前第二短序列调整的方式不作限制。
[0105]
在本发明的一实施例中，若后一第二拆分序列对应二进制补码序列的最高位的值为1时，则可以先对当前第二拆分序列对应的第二短序列执行按位取反操作，再将所述按位取反操作后得到的二进制补码序列进行标记，得到当前第二拆分序列对应的标记后的二进制补码序列，并将所述标记后的二进制补码序列输入至有符号乘法器。若后一第二拆分序列对应二进制补码序列的最高位的值为0，则保持第二拆分序列当前对应的第二短序列输
入至有符号乘法器。
[0106]
关于具体如何对第二短序列进行按位取反，可以参照上述关于如何对第一短序列进行取反的描述，进行实施，此处不再赘述。
[0107]
步骤44，将乘法操作结果进行移位累加，得到所述第一操作数及第二操作数的乘法运算结果。
[0108]
在一些实施例中，当后一第一拆分序列对应二进制补码序列的最高位的值为0时，以及依据后一第二拆分序列对应二进制补码序列的最高位的值也为0时，第一短序列及第二短序列将被送入到实例化的乘法器中可得到分部积，再对分部积进行处理可以得到正确的结果。
[0109]
在一些实施例中，当后一第一拆分序列对应二进制补码序列的最高位的值为1时，第一短序列对应的第一输入序列将被送入至有符号乘法器。当后一第二拆分序列对应二进制补码序列的最高位的值为1时，第二短序列对应的第二输入序列将被送入至有符号乘法器。通过对有符号乘法器的分部积进行处理可以得到正确的结果。
[0110]
在本发明的一实施例中，确定所述乘法操作结果对应的第一输入序列及第二输入序列后，可以基于所述第一输入序列对应的下一第一拆分序列最高位的值，及所述第二输入序列对应的下一第二拆分序列最高位的值，对所述乘法操作结果进行正负调整，并对调整后的乘法操作结果进行移位累加。
[0111]
以第一输入序列s
i
及第二输入序列r
j
为例，第一输入序列s
i
对应的第一短序列为第一短序列为对应的第一拆分序列为p
i
，故第一输入序列s
i
对应的下一第一拆分序列为p
i
‑1。第二输入序列r
j
对应的第二短序列为第二短序列为对应的第二拆分序列为q
j
，故第二输入序列r
j
对应的下一第二拆分序列为q
j
‑1。将第一输入序列s
i
及第二输入序列r
j
送入到乘法器中可得到分部积z
i,j
＝r
i
·
s
j
，具体可以参照图5。
[0112]
假设第一输入序列s
i
对应的下一第一拆分序列p
i
‑1最高位的值为c
s,i
‑1，第二输入序列r
j
对应的下一第二拆分序列最高位的值为c
r,j
‑1，在得到分部积z
i,j
后，可以由的值来确定是否要对分部积z
i,j
进行正负形调整，即是否要对分部积z
i,j
取相反数。
[0113]
在具体实施中，利用同样输入位宽的有符号乘法器，可以实现对多种位宽的操作数的乘法操作。
[0114]
例如，以有符号乘法的输入位宽为8比特，并对位宽均为32比特的两操作数进行乘法操作时，假设第一操作数x＝(8f927f81)
hex
，第二操作数y＝(34ff80c1)
hex
，由上述关于步骤41及43的描述，可以得到第一操作数x对应的完整拆分结果为：
[0115]
x＝8f927f81＝((70)
s
·
(
‑
1))(92)
s
((80)
·
(
‑
1))
s
(81)
s
。
[0116]
由上述关于步骤42及43的描述，可以得到第二操作数y各第二短序列对应的第二输入序列，并得到第二操作数y对应的完整拆分结果为：
[0117]
y＝((cb)
s
·
(
‑
1))((00)
s
·
(
‑
1))((7f)
s
·
(
‑
1))(c1)
s
。
[0118]
将各个第一输入序列及第二输入序列输入至有符号乘法器后，乘法操作的结果如
表1所示。参照表1，例如，第一输入序列(cb)
s
与第二输入序列(70)
s
相乘，根据记录二者的
‑
1互相抵消，而c1与70相乘其结果还要做一次乘以
‑
1的纠正。第一操作数x与第二操作数y对应的分部积中，需要纠正的结果在表1中标记为深色。
[0119]
表1：
[0120][0121]
对表1中深色位置处的分部积结果进行纠正，即将表1中深色位置处的分部积结果乘以(
‑
1)，修正后的结果如表2所示：
[0122]
表2：
[0123][0124]
在具体实施中，对修正后的分部积进行移位累加时，可以存在多种操作。在一实施例中，以表2为例，可以将表2中每四个单元格构成一组，将该组内沿对角线分部的两分部积拼接后，再将拼接的结果相加，最后对相加结果再进行移位，得到移位结果z0、z1、z2及z3，最后将移位结果z0、z1、z2及z3，先拼接再相加，最后移位。具体地：
[0125]
z0＝(e8d00000)
hex
+(e93a+0000)
hex
<<8；
[0126]
z1＝(37901b12)
hex
+(3692+1b90)
hex
<<8；
[0127]
z2＝(1a800000)
hex
+(e5b5+0000)
hex
<<8；
[0128]
z3＝(c0801f41)
hex
+(3f01+e080)
hex
<<8。
[0129]
再将z0、z1、z2及z3以同样方式操作，得到第一操作数及第二操作数的乘法运算结果z：
[0130]
z＝(z0z3)
hex
+(z1+z2)
hex
<<16。
[0131]
利用输入位宽为8比特的有符号乘法器，对位宽均为64比特的两操作数进行乘法操作时，假设第一操作数x＝(7348)
hex
(a19f)
hex
(8f92)
hex
(7f81)
hex
，第二操作数y＝(b518)
hex
(ffff)
hex
(34ff)
hex
(80c1)
hex
。x、y均包括4个有符号的16位数据，每个有符号的16位数据，称为一个元素。第一操作数x与第二操作数y的点乘结果z，是x、y中对应的元素相乘的结果。
[0132]
根据关于步骤41的描述，可以得到第一操作数x对应的第一拆分序列为：x＝[(73)
(48)][(a1)(9f)][(8f)(92)][(7f)(81)]。根据关于步骤42的描述，可以得到第二操作数y对应的第二拆分序列为：y＝[(b5)(18)][(ff)(ff)][(34)(ff)][(80)(c1)]。
[0133]
根据关于步骤43的描述，可以得到第一操作数x各第一拆分序列对应的第一输入序列，从而得到第一操作数x的完整拆分结果：
[0134]
x＝[(73)
s
(48)
s
][((5f)
s
·
(
‑
1))(9f)
s
][((70)
s
·
(
‑
1))(92)
s
][((80)
s
·
(
‑
1))(81)
s
]。
[0135]
根据步骤43的描述，可以得到第二操作数y各第二拆分序列对应的第二输入序列，从而得到第二操作数y的完整拆分结果：
[0136]
y＝[(b5)
s
(18)
s
][((00)
s
·
(
‑
1))(ff)
s
][((cb)
s
·
(
‑
1))(ff)
s
][((7f)
s
·
(
‑
1))(c1)
s
]。
[0137]
将上述第一输入序列及第二输入序列输入至有符号乘法器，可以得到分部积结果如表3所示：
[0138]
表3：
[0139][0140]
对表3中分部积结果进行移位累加时，与上述对位宽为32比特的操作数的移位相同，可以得到移位结果z0、z1、z2及z3：
[0141]
z0＝(e8d0006e)
hex
+(e93a+0070)
hex
<<8
[0142]
z1＝(514f06c0)
hex
+(32e8+0ac8)
hex
<<8；
[0143]
z2＝(00009e61)
hex
+(a15f+0000)
hex
<<8；
[0144]
z3＝(c0801f41)
hex
+(3f01+e080)
hex
<<8
[0145]
移位结果z0、z1、z2及z3就是第一操作数x与第二操作数y对应的元素乘积的结果。
[0146]
本发明的实施例中，当有符号乘法器的输入位宽m确定后，比如，上述实施例中，有符号乘法器的输入位宽m＝8，则对不同类型的乘法，如32比特的乘法(即操作数位宽为32比特)、16比特的乘法(即操作数位宽为16比特)或8比特乘法(即操作数位宽为8比特)，甚至混合位宽乘法(如24比特的操作数乘以16比特的操作数)，都可以使用本发明实施例中描述的步骤进行处理，即对应不同模式的乘法可以具有相同的处理过程，简化了兼容设计不同模式乘法的复杂度。得到乘法操作后，如何进行移位累加，根据所要求的乘法类型(也就是所输入的操作数的位宽)来决定即可。
[0147]
当m＝16时，相对于m＝8时，同样的操作数，但仅用了四分之一数量的16位有符号乘法器。可以理解的是，本发明实施例中，上述m＝16的实施例，仅是用于与m＝8的实施例进行对比，实际使用时，通常是调整输入操作数的位宽为64比特，由此可以同时进行4个16比
特的乘法。
[0148]
需要说明的是，实际应用中，有符号乘法器的输入位宽m，具体可以根据操作数的位宽等因素所确定的实际需求进行设定。无论有符号乘法器的输入位宽m如何，均可以采用本发明实施例中的运算控制方法进行运算控制。
[0149]
图6为本发明实施例中运算过程的一种示意图。参照图6，当有符号乘法器的输入位宽为m比特时，若输入的第一操作数x的位宽为4m比特，可以将第一操作数转换为4个位宽为m比特的第一短序列x0、x1、x2及x3，并标记每个第一短序列x0、x1、x2及x3的符号s0、s1、s2及s3。之后，对第一短序列x0、x1、x2及x3，分别进行按位取反，得到相应的第一输入序列x0’、x1’、x2’及x3’。
[0150]
同样地，若输入的第二操作数y的位宽为4m比特，可以将第二操作数y转换为4个位宽为m比特的第二短序列y0、y1、y2及y3，并标记每个第二短序列y0、y1、y2及y3的符号r0、r1、r2及r3。之后，对第二短序列y0、y1、y2及y3，分别进行按位取反，得到相应的第二输入序列y0’、y1’、y2’及y3’。
[0151]
将第一输入序列x0’、x1’、x2’及x3’，以及第二输入序列y0’、y1’、y2’及y3’，输入至16个m比特的有符号乘法器，得到乘法操作结果t0至t16。然后基于之前记录的符号，对乘法操作结果t0至t16进行符号调整，使得每个调整后的乘法操作结果均为m比特的有符号乘法输出结果。将调整后的乘法操作结果中，每4个单元格进行移位相加，移位相加结果进行累加，得到4m比特的有符号乘法运算结果。
[0152]
可以理解的是，本本发明的实施例，可以任意调整第一输入序列及第二输入序列个数及位宽，实现相应的乘法运算控制。比如，可以实现2m比特与m比特的乘法，4m比特与m比特的乘法，4m比特与2m比特的各种乘法，且都采用同样的处理流程。
[0153]
具体地，当操作数的位宽为m比特时，由于操作数的位宽与有符号乘法器的输入位宽相等，此时无需对操作数x进行拆分，直接记录该操作数的符号，并得到相应的输入序列即可。
[0154]
当操作数的位宽为2m比特时，可以先将操作数拆分为两个拆分序列，并记录该拆分序列的符号，确定相应的输入序列。比如，可以将第一操作数x拆分为第一拆分序列x0及x3，并记录第一拆分序列x0及x3的符号后，确定第一输入序列x0’及x3’，再输入至乘法器进行乘法操作即可。
[0155]
从图6可以看出，第一操作数x拆分成m比特后，只会进行按位取反这一个操作，其是否按位取反只取决于操作数的位宽以及有符号乘法器的输入位宽。比如进行m位乘法运算时，拆分短序列就是m位，不存在后一短序列。当进行2m位乘法时，每2个m位短序列中最后的序列也是不取反的。是否执行按位取反操作，无需关注后一个第一拆分序列所有比特的情况，复杂度大大简化，尤其是在数据通路上逻辑很简单。
[0156]
另外，在输出端，取相反数的位置只存在于乘法操作后，即只对乘法器输出的乘法操作结果(t0～t15)执行取相反数操作。相对于移位累加结果执行取相反数操作(参照如2及图3)，一方面，乘法操作结果的位宽更小，对其执行取相反数操作难度也就更小；另一方面，在乘法运算过程中，对不同乘法操作结果执行移位次数可能并不相同，故硬件实现时，对移位累加结果执行取相反数操作的模块，位置并不固定，导致实现难度大，而对乘法操作结果执行取相反数操作时，执行取相反数操作的模块位置固定，降低实现难度。
[0157]
并且，无论输入的操作数位宽如何，以及两个操作数的位宽是否相同，均可以使用同样的有符号乘法器进行乘法操作，有符号乘法器的复用度很高，更适合在gpu、npu设计中采用大规模阵列的场景，具有一致同构的结构特征。
[0158]
比如，一个32位操作数乘以另一32位数操作，假设短序列长度m＝8时，可以采用输入位宽为4m的有符号乘法器类型来实现乘法操作。一个16位操作数乘以另一16位操作数，假设短序列长度m＝8，仍可以采用输入位宽为4m的有符号乘法器类型来实现乘法操作。
[0159]
本发明实施例中，有符号乘法器的数量，通常可以为4的整次幂，比如，运算控制系统可以包括64个8位的有符号乘法器，利用该64个8位的有符号乘法器，可以得到4个32位的乘法操作结果，也可以得到16个16位的乘法操作结果，还可以得到64个8位的乘法操作结果。在有符号乘法器的输入位宽及数量固定的情况下，可以根据用户需求，可以得到不同位宽的乘法操作结果，故灵活性更高。为了使本领域技术人员更好地理解和实现本发明，以下对上述方法对应的用户终端及计算机可读存储介质进行详细描述。
[0160]
参照图7，本发明实施例还提供了一种运算控制装置70，所述运算控制装置70可以包括：第一转换单元71、第二转换单元72、运算控制单元73及移位累加单元74。其中：
[0161]
所述第一转换单元71，适于获取第一操作数，并将所述第一操作数转换为若干个第一短序列，每个第一短序列均为二进制补码表示的有符号数；
[0162]
所述第二转换单元72，适于获取第二操作数，并将所述第二操作数转换为若干个第二短序列，每个第二短序列均为二进制补码表示的有符号数；
[0163]
所述运算控制单元73，适于将所述第一短序列及第二短序列输入至有符号乘法器，控制所述有符号乘法器，对所述第一短序列及第二短序列执行乘法操作；
[0164]
所述移位累加单元74，适于将乘法操作结果进行移位累加，得到所述第一操作数及第二操作数的乘法运算结果；
[0165]
其中，所述第二短序列的个数与所述第一短序列的个数相同；所述第一短序列及第二短序列的位宽与所述有符号乘法器的输入位宽相同；所述有符号乘法器的个数，大于或等于所述第一短序列的个数
[0166]
关于所述运算控制装置70包含的各个功能单元，具体可以参照上述关于运算控制方法中相应步骤的描述进行实施，此处不再赘述。
[0167]
参照图8，本发明实施例还提供了一种运算控制系统，所述运算控制系统包括上述的运算控制装置70，以及若干个有符号乘法器80。
[0168]
所述运算控制装置70可以与所述有符号乘法器80连接；所述有符号乘法器80适于在所述运算控制装置70的控制下执行乘法操作；所述有符号乘法器80的个数，大于或等于所述运算控制装置70中第一短序列的个数。
[0169]
在具体实施中，所述运算控制装置70可以将第一短序列及第二短序列、第一短序列及第二输入序列、第一输入序列及第二短序列、或者第一输入序列及第二输入序列，输入至有符号乘法器80中，并控制有符号乘法器80对其执行乘法操作。在乘法操作后，所述运算控制装置70可以获取乘法操作结果，并执行移位累加操作，最终输出第一操作数及第二操作数的最终乘法运算结果。
[0170]
本发明实施例还提供了一种处理器，所述处理器包括上述的运算控制系统。
[0171]
在具体实施中，所述处理器可以为npu，也可以为处理器，具体不作限制。
[0172]
利用所述处理器，可以利用若干个有符号乘法器，实现任意位宽的两操作数的乘法操作，整体运算控制简单，复杂度较低。
[0173]
本发明实施例还提供了一种计算机可读存储介质，其上存储有计算机程序，所述计算机程序被处理器执行，以实现上述运算控制方法的步骤，不再赘述。
[0174]
在具体实施中，所述计算机可读存储介质可以包括：rom、ram、磁盘或光盘等。
[0175]
关于上述实施例中描述的各个装置、产品包含的各个模块/单元，其可以是软件模块/单元，也可以是硬件模块/单元，或者也可以部分是软件模块/单元，部分是硬件模块/单元。例如，对于应用于或集成于芯片的各个装置、产品，其包含的各个模块/单元可以都采用电路等硬件的方式实现，或者，至少部分模块/单元可以采用软件程序的方式实现，该软件程序运行于芯片内部集成的处理器，剩余的(如果有)部分模块/单元可以采用电路等硬件方式实现；对于应用于或集成于芯片模组的各个装置、产品，其包含的各个模块/单元可以都采用电路等硬件的方式实现，不同的模块/单元可以位于芯片模组的同一组件(例如芯片、电路模块等)或者不同组件中，或者，至少部分模块/单元可以采用软件程序的方式实现，该软件程序运行于芯片模组内部集成的处理器，剩余的(如果有)部分模块/单元可以采用电路等硬件方式实现；对于应用于或集成于终端的各个装置、产品，其包含的各个模块/单元可以都采用电路等硬件的方式实现，不同的模块/单元可以位于终端内同一组件(例如，芯片、电路模块等)或者不同组件中，或者，至少部分模块/单元可以采用软件程序的方式实现，该软件程序运行于终端内部集成的处理器，剩余的(如果有)部分模块/单元可以采用电路等硬件方式实现。
[0176]
虽然本发明披露如上，但本发明并非限定于此。任何本领域技术人员，在不脱离本发明的精神和范围内，均可作各种更动与修改，因此本发明的保护范围应当以权利要求所限定的范围为准。