一种电力区域负荷的图神经网络预测方法

1.本发明涉及区域电力负荷预测领域，具体涉及一种电力区域负荷的图神经网络预测方法。


背景技术：

2.精准的负荷预测作为电力系统状态估计、保证其安全稳定运行，并实现其优化调度控制的前提与基础工作，在电力系统中具有重要地位，当前已经有一部分公开的报道初步表明疫情对负荷变化的影响，其最终大多得到了“大流行期间用电量有所减少，但电网仍然可靠”这类偏定性的结论。(q.bui and j.wolfers,“another way to see the recession:power usage is waydown,”new york times,apr.2020.accessed:may 6,2020.)(s.cicala,“early economic impactsof covid
‑
19 in europe:a view from the grid,”univ.chicago,chicago,il,usa,tech.rep. accessed:may 6,2020.[online].available:https://home.uchicago.edu /～scicala/papers/real_time_eu/real_time_eu.pdf)然而，实际上疫情对电力负荷水平的作用并不能用简单的减少来加以概括，实际上有研究已经表明这种影响可能是多个方面，而当前负荷预测的方法难以涵盖疫情的影响。(agdas d,barooah p.impact of the covid
‑
19 pandemic onthe u.s.electricity demand and supply:an early view from data[j].ieee access,2020,pp(99):1
‑
1.) (werth a,gravino p,prevedello g.impact analysis of covid
‑
19 responses on energy griddynamics in europe[j].applied energy,2020,281.)同时，有研究通过对比不考虑疫情作用下的传统负荷预测方法所得的预测负荷结果与真实的负荷情况直接的差距，得出了疫情切实对负荷水平造成了影响，并表明了传统负荷预测方法并不能很好的反映这种影响。(ruan g,wud,zheng x,et al.a cross
‑
domain approach to analyzing the short
‑
run impact of covid
‑
19 onthe u.s.electricity sector[j].arxiv,2020.)此外，随着新型电力系统的不断建设，高比例可再生能源渗透的特征愈发突出。除发电侧中的新能源装置占比越来越大外，负荷侧也出现了光伏以及储能等装置广泛应用的现象，负荷从传统的电力消费者逐步转向了具有“源
‑
荷”二重性的产消者(陈玥,刘锋,魏韡,梅生伟.需求侧能量共享：概念、机制与展望[j].电力系统自动化,2021,45(02):1
‑
11.胡俊杰,王坤宇,艾欣,韩雪,杨光亚,薛禹胜.交互能源:实现电力能源系统平衡的有效机制[j].中国电机工程学报,2019,39(04):953
‑
966.)，随之带来了负荷侧电力消费水平的高度不确定性，这给精确的负荷预测带来了巨大困难。可以说，传统负荷预测方法更多的集中于考虑时序负荷数据的回归分析，较少考虑风速、光照等因素的影响，故而难以胜任新型电力系统下的电力产消者的负荷预测工作。因此，在疫情长期发展以及新型电力系统中电力消费高度不确定的大背景下，如何设计一种负荷预测方法，合理考虑多种影响因素，实现区域负荷的精准预测，是当前电力系统亟需解决的一个重要问题。


技术实现要素：

[0003]
目前大多数负荷预测算法难以考虑疫情下政策、群众心理的变化，从而导致实际工程运用中精度下降的问题，本发明提出一种电力区域负荷的图神经网络预测方法，用于疫情下的区域负荷精准预测，有效地提高疫情这类重大社会事故爆发下负荷预测的精度。
[0004]
本发明的目的至少通过如下技术方案实现。
[0005]
一种电力区域负荷的图神经网络预测方法，包括如下步骤：
[0006]
步骤1、基于智能电网数据采集与监视控制系统获取的区域电气数据特征以及包括疫情态势及气象在内的多种外源信息，建立区域电力特征库，提取出负荷预测的训练集、验证集和测试集；
[0007]
步骤2、对多种外源信息进行分析，挖掘各个信息数据之间以及信息与预测对象之间的关联关系，采用斯皮尔曼相关系数与皮尔逊相关系数对关联关系进行量化表征；
[0008]
步骤3、将多种外源信息及其关联关系转换成包含节点和边的图结构数据，获取区域负荷信息图；
[0009]
步骤4、构建深度图残差卷积网络，对当前区域负荷信息图与未来电力负荷数据的非线性映射关系进行学习，并在深度图残差卷积网络的基础上串联全连接层，从而构建负荷预测模型，实现区域负荷信息图到预测目标功率的非线性映射；
[0010]
步骤5、将训练集中的训练样本分成若干个批次并按批次送入负荷预测模型中进行训练，并用验证集对负荷预测模型的超参数进行调整直至收敛，用调整后的负荷预测模型进行区域电力负荷预测。
[0011]
优选的，步骤2包括以下步骤：
[0012]
首先获取实时传输的区域有功功率序列作为实时电力负荷功率数据，其中p
sum
(t)为t时刻区域的用电负荷总量，t为功率序列时间窗口长度，同时从历史负荷数据中选取预测负荷时段对应时段的负荷数据作为历史同期电力负荷功率特征；
[0013]
其次在外源信息中选取包括covid
‑
19病毒相关疫情态势数据以及风速、天气信息、温度信息、电价信息、法定节假日信息数据，作为主要特征进行考虑分析；所述covid
‑
19病毒相关疫情数据包括新冠病毒阳性确诊病例以及接种疫苗人数信息、交通和购物人流趋势的流动等相关信息；
[0014]
采用斯皮尔曼与皮尔逊或是其他相关系数反映各个特征之间、以及各个特征与未来负荷之间的相关关系，对各个特征信息之间以及特征信息与待预测的未来负荷之间的关联关系进行量化评估。
[0015]
优选的，皮尔逊相关系数为：
[0016][0017]
式中：n为样本数量，i为样本；x
i
和y
i
为待分析对象信息的观测值；r
p
为pearson线性相关系数，分别表示分析对象信息的平均数值；
[0018]
pearson线性相关系数取值范围是[
‑
1,1]，r
p
＝1表示为完全正相关，r
p
＝
‑
1为完全
负相关， r
p
＝0表示不存在线性相关关系，|r
p
|越接近于1线性相关程度越好，|r
p
|越接近于0线性相关程度越弱；
[0019]
spearman秩相关系数为排列后的变量之间的pearson线性相关系数，其计算方法如下：对待分析对象信息的观测值为x
i
和y
i
按从大到小的顺序排列，并记x
i
′
和y
i
′
为原数据x
i
和y
i
在排列后数据所在的位置，则x
i
′
和y
i
′
称为变量x
i
和y
i
的秩次：
[0020][0021]
d
i
＝x
i
′‑
y
i
′
[0022]
式中：n为样本数量；x
i
和y
i
为两变量的变量值；r
s
即为spearman线性相关系数；d
i
为 x
i
与y
i
的秩次之差；
[0023]
spearman秩相关系数的符号表示待分析对象x
i
和y
i
之间的相关方向，当x
i
随y
i
的增加而增加，则相关系数为正数；当x
i
随y
i
的增加而减小，则相关系数为负数，当x
i
随y
i
相关系数的绝对值为1时表示变量之间满足严格的单调函数关系。
[0024]
优选的，步骤3中，所述的区域负荷信息图中，每个节点表示实时负荷信息及多种外源信息中的一项信息数据，各个节点两两相连由此形成图中的边，其中边的数值由信息数据之间的关联关系所决定，代表不同信息节点之间所存在的隐含关系。
[0025]
优选的，对各节点数据进行标准化转化，具体如下，对于功率数值的连续性节点特征，利用max
‑
min标准化方法对数据进行线性变换，将数据映射到[0,1]区间，其定义如下：
[0026][0027]
式中：x、x
*
分别为连续型特征数据的原始值和标准化转化值；max是数据中的最大值； min是数据中的最小值；
[0028]
对于是否为工作日这类离散型节点特征，则利用one
‑
hot编码进行处理。
[0029]
优选的，所述深度图残差卷积网络包括若干个残差图卷积模块以及长跳跃连接，每个残差图卷积模块包括若干个残差图卷积网络层，利用短跳跃连接将若干个残差图卷积网络层连接。
[0030]
优选的，所述深度图残差卷积网络对输入的每一个包含原始特征信息的无向图g(a,x)，使用图卷积层对其进行信息聚合，输出新无向图g(a,x
′
)：
[0031][0032]
式中：分别为节点i、j在第k与k
‑
1层图卷积层的数值；n(i)、{i}表示节点 i的邻居节点集合及节点i；θ为权重矩阵；deg(i)和deg(j)表示节点i和节点j的度；σ表示激活函数；e
i,j
表示连接节点i,j的边的数。
[0033]
优选的，残差图卷积网络层为：
[0034][0035]
式中：α
θ
表示原始特征的残差衰减因子；β表示权重矩阵的衰减因子；i
n
为单位矩阵；
[0036]
优选的，步骤4中，所述负荷预测模型使用全连接层对输入的区域负荷信息图进行特征变换，对所述深度图残差卷积网络提取的图数据的结构特征使用图池化层聚合全图信息，最后使用全连接层实现聚合所得的全图信息到预测目标功率的非线性映射。
[0037]
优选的，步骤5包括将训练集中的训练样本分成若干个批次进行训练，使用图拼接的方式实现多图并行化计算，并引入早停机制机制提前终止训练，提高模型泛化性；
[0038]
图拼接是将多个图的邻接矩阵和特征矩阵按对角线分别进行拼接，形成总的稀疏的邻接矩阵和特征矩阵，所述总的稀疏的邻接矩阵和特征矩阵包括多个孤立子图的巨型图，同时，基于深度图残差卷积网络中的权值共享机制。
[0039]
相比于现有技术，本发明的有益效果如下：
[0040]
本发明利用区域用电负荷信息以及区域covid
‑
19病毒相关疫情数据、天气、经济等多维外源数据信息构建区域负荷信息图，并使用深度残差图神经网络进行未来负荷的预测。首先将获得的所有区域信息转换成包含节点和边的图数据，将其中的负荷信息与外源信息定义为节点特征，潜在的信息关联关系定义为边的权重，构建带有关联知识的区域负荷信息图，实现多源信息在图数据中的融合，并引入带残差机制的深度图残差卷积网络对图数据内部的有效信息进行学习，其中采用多图并行化的方式加速训练，引入earlystopping机制(早停机制)提前终止训练，提高模型的泛化性，构建区域负荷信息到未来负荷之间的非线性映射关系，最终实现区域电力负荷的精准预测。本发明具有逻辑清晰、计算速度快、预测精度高、能充分利用外源信息的特点。以图数据的形式，构建带有多源信息内部关联知识的区域负荷信息图，相比不带知识信息的常规负荷预测模型复杂度更低，能更有效地提高负荷预测的准确率，为实现电网跨区域优化调度与安全稳定控制打下坚实基础，为保障电网安全稳定运行提供有力的技术支持。
附图说明
[0041]
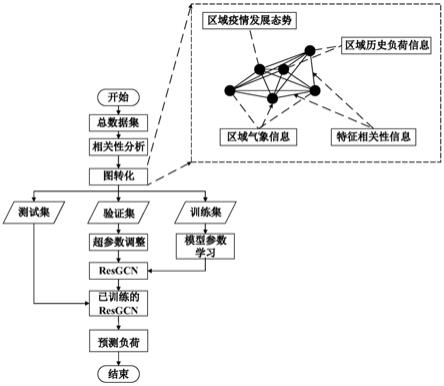
图1是本发明实施例中区域负荷信息图的图构建方式示意图；
[0042]
图2是本发明实施例中gcn和resgcn的卷积过程对比示意图；
[0043]
图3是本发明实施例中基于深度图残差卷积网络的负荷预测模型的结构示意图；
[0044]
图4是本发明实施例中多图并行化示意图；
[0045]
图5是本发明实施例中整体实施的流程图。
具体实施方式
[0046]
附图仅用于示例性说明，不能理解为对本专利的限制；为了更好说明本实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。附图中描述位置关系仅用于示例性说明，不能理解为对本专利的限制。
[0047]
实施例一：
[0048]
一种电力区域负荷的图神经网络预测方法，如图1、图5所示，包括如下步骤：
[0049]
步骤1、基于智能电网数据采集与监视控制系统获取的区域电气数据特征以及区域卫生部、气象部等其他信息源公布的外源信息，建立的区域电力特征库，提取出负荷预测的训练集、验证集和测试集；
[0050]
所述智能电网数据采集与监视控制系统获取的区域电气数据特征以及区域卫生部、气象部等其他信息源公布的外源信息，智能电网数据采集与监视控制系统方面主要采用其中有功功率等稳态特征进行分析，而考虑到区域卫生部、气象部等其他信息源获取困难，此处利用先进的数据爬虫手段对网络上的外源数据资源进行收集，利用多源信息数据构建区域电力特征库，并按6:2:2的比例划分训练集、验证集和测试集。
[0051]
步骤2、基于相关性理论对多源信息进行分析深度挖掘各个信息数据之间以及信息与指定预测对负荷之间的关联关系，并计算斯皮尔曼(spearman)相关系数与皮尔逊(pearson) 相关系数等将关联关系进行量化表征；
[0052]
基于相关性理论对多源信息进行分析深度挖掘各个信息数据之间以及信息与预测对象之间可能存在的同向增长或反向抑制等关联关系，并计算spearman与pearson等系数将其量化表征，具体包括：
[0053]
首先获取实时传输的区域有功功率序列按某一固定窗口t(将窗口设置为24h)，将其作为实时电力负荷功率数据，同时从历史负荷数据中选取预测负荷时段一个礼拜及一个月前对应时段的负荷数据作为同期电力负荷序列作为历史同期电力负荷功率特征；
[0054]
其次在外源数据信息中选取新冠病毒阳性确诊病例以及接种疫苗人数信息、交通和购物人流趋势等人口近期流动信息、风速、光照等天气信息、温度信息、电价信息、法定节假日信息作为主要特征进行考虑分析。最后为反映各个特征之间，以及各个特征与未来负荷之间的相关关系，采用spearman与pearson相关系数两个指标进行量化评估，其计算方式如下：
[0055]
pearson相关系数可由下式进行计算得到：
[0056][0057]
式中：n为样本数量，i为样本；x
i
和y
i
为待分析对象信息的观测值；r
p
为pearson线性相关系数，分别表示分析对象信息的平均数值；
[0058]
pearson线性相关系数取值范围是[
‑
1,1]，r
p
＝1表示为完全正相关，r
p
＝
‑
1为完全负相关， r
p
＝0表示不存在线性相关关系，|r
p
|越接近于1线性相关程度越好，|r
p
|越接近于0线性相关程度越弱；
[0059]
spearman秩相关系数是排列后的变量之间的pearson线性相关系数，其计算方法如下：同样设待分析对象信息的观测值为x
i
和y
i
，按从大到小的顺序对其重新排列，并记x
i
′
和y
i
′
为原数据x
i
和y
i
在排列后数据所在的位置，则x
′
i
和y
′
i
称为变量x
i
和y
i
的秩次。
[0060][0061]
d
i
＝x
′
i
‑
y
′
i
[0062]
式中：n为样本数量；x
i
和y
i
为两变量的变量值；r
s
即为spearman线性相关系数；d
i
为 x
i
与y
i
的秩次之差；
[0063]
spearman秩相关系数的符号表示待分析对象x与y之间的相关方向，当x随y的增加而增加，则相关系数为正数；当x随y的增加而减小，则相关系数为负数，当x与y相关系数的绝对值为1时表示变量之间满足严格的单调函数关系。
[0064]
步骤3、基于图理论将多源信息及其步骤2所得的关联关系转换成包含节点和边的图结构数据，获取区域负荷信息图；
[0065]
在区域负荷信息图中每个节点表示实时负荷信息及多种外源信息中的一项信息数据，各个节点两两相连由此形成图中的边，其中边的数值则由步骤2中所得的关联关系所决定，代表着不同信息节点之间所存在的隐含关系。同时，为使后续人工智能方法有效地挖掘图中深层的信息，需对各节点数据进行标准化转化，具体过程如下：对于功率数值等连续性节点特征，利用max
‑
min标准化方法对数据进行线性变换，将数据映射到[0,1]区间，其定义如下
[0066][0067]
式中：x,x
*
分别为连续型特征数据的原始值和标准化转化值；max是该数据中的最大值； min是该数据中的最小值；
[0068]
对于是否为工作日这类离散型节点特征，则利用one
‑
hot编码进行处理，避免简单十进制编码下多次加权运算造成误差，更便于预测网络进行精准学习。
[0069]
步骤4、构建深度图残差卷积网络对区域负荷信息图与未来电力负荷数据的非线性映射关系进行学习，实现特征的传递、转换和学习，并以此构建基于深度图残差卷积网络的负荷预测模型，实现区域负荷信息图到预测目标功率的非线性映射；
[0070]
例如若选取2020.08.05某区域的负荷数据为未来预测对象，其即为未来电力负荷数据，需要构造相对应的区域负荷信息图对其进行计算。
[0071]
所述构建深度图残差卷积网络对区域负荷信息图与未来电力负荷数据的非线性映射关系进行学习，实现特征的传递、转换和学习中的深度图残差卷积网络，具体如下：
[0072]
图卷积层(graph convolutional network,gcn)在聚合邻居节点信息，对于每一个包含原始特征信息的输入无向图g(a,x)，使用图卷积层对其进行信息聚合，输出更抽象、更具辨识度的新无向图g(a,x
′
)。
[0073]
对于图上任意节点，每进行一次卷积操作，节点信息就更新一次，就聚合了更高一阶相邻节点的信息。由于gcn层堆叠层数增多，每个节点融合了全图节点的信息，导致节点多样性开始下降，节点信息趋向一致，从而出现过度平滑现象。为了解决这个问题，本发明引入长短跳跃残差机制的深度图残差卷积网络，其包括三层图残差卷积模块(resgcn
‑
block,rb)，每个图残差卷积模块包括三个图残差卷积层(residual graph convolutional network,resgcn) 以及一个长跳跃连接，即图3负荷预测模型中的结构所示(图中n为网络层神经元个数)。其中gcn的特征提取方式如图2的上半部所示，通过对邻居节点消息的传递，转换和聚合实现特征的提取，该过程用以下式子表示：
[0074][0075]
式中：分别为节点i,j在第k与k
‑
1层的数值；n(i)、{i}表示节点i的邻居
节点集合及其本身；θ为权重矩阵；deg(i)和deg(j)表示节点i和节点j的度；σ表示激活函数；e
i,j
表示连接节点i,j的边的数；
[0076]
残差机制主要是增加图卷积网络深度的同时，加入初始残差连接和恒等映射。对于每一层，初始残差从输入层构建一个跳跃连接，保证了每个节点的信息随着卷积次数的增多始终能保留初始输入特征的一部分；恒等映射则在权值矩阵中添加一个单位矩阵，保证深度模型至少与浅层模型的性能相同，即resgcn层如图2的下半部所示，表达为：
[0077][0078]
式中：α
θ
表示原始特征的残差衰减因子；β
l
表示权重矩阵的衰减因子；i
n
为单位矩阵。
[0079]
图2展示了resgcn与gcn卷积过程的区别。
[0080]
为实现区域负荷精准预测，构建基于深度图残差卷积网络的负荷预测模型。模型的输入为由步骤3中构建的区域负荷信息图，输出为该未来预测时刻的负荷功率值。首先，模型使用1个全连接层进行特征变换，其次使用上述深度图残差卷积网络提取图数据的结构特征，然后使用1个图池化层聚合全图信息，最后使用4个全连接层实现区域负荷信息图到预测目标功率的非线性映射，构成负荷预测模型。整体结构如图3所示。
[0081]
步骤5、将训练集中的训练样本分成若干个批次并按批次送入网络中进行训练，采用固定学习率的方式训练，并基于验证集与启发式算法对网络模型的超参数进行调整，反复的训练直至收敛，并以之实现高精度的区域电力负荷预测。
[0082]
所述将训练集中的训练样本分成若干个批次进行训练，是指使用图拼接的方式实现多图并行化，这是因为位于非欧式空间的图数据不能简单地将一批次的图数据同时输入模型，不利于模型的高效训练。
[0083]
本发明的图拼接是将由第1幅图g1(a,x)到第n幅图g
n
(a,x)的邻接矩阵{x1,x2,
…
,x
n
} 和特征矩阵{a1,a2,
…
,a
n
}按对角线分别进行拼接，形成一个总的稀疏的邻接矩阵和特征矩阵，从而创建出包含多个孤立子图的巨型图，具体过程如图4中所示。由于图卷积网络中的权值共享机制，将该巨型图送入resgcn中的训练结果与将多个子图分别进行训练所得结果相同，故可节省模型训练时间，大幅提升训练效率。
[0084]
实施例二：
[0085]
步骤5中，将训练集中的训练样本分成若干个批次并按批次送入负荷预测模型中进行训练，采取指数衰减学习率调整的方法优化训练过程，并用验证集对负荷预测模型的超参数进行调整直至收敛，用调整后的负荷预测模型进行区域电力负荷预测。
[0086]
该实施例考虑了学习率对预测模型训练的影响，引入指数衰减学习率调整的方法优化训练过程，指数衰减学习率调整方法可表示为：
[0087]
ir(i)＝ir
origin
×
r
decay
^(i/n
decay
)
[0088]
式中，ir(i)表示第i轮迭代时的学习率；ir
origin
表示初始设定的学习率；r
decay
指代衰减率系数，取值在[0,1]之间；i代表当前迭代所处的轮次；n
decay
表示衰减周期。
[0089]
对其进行求导可得下式：
[0090]
[0091]
同时由r
decay
∈[0,1]可知，ln(r
decay
^(1/n
decay
))＜0及该学习率导数为负数，学习率递减，可有效优化训练过程，避免学习率过大导致的不收敛问题。
[0092]
实施例三：
[0093]
步骤5中，将训练集中的训练样本分成若干个批次并按批次送入负荷预测模型中进行训练，采取固定步长衰减学习率调整的方法优化训练过程，并用验证集对负荷预测模型的超参数进行调整直至收敛，用调整后的负荷预测模型进行区域电力负荷预测。
[0094]
该实施例考虑了学习率对预测模型训练的影响，引入固定步长衰减学习率调整的方法优化训练过程，固定步长衰减学习率调整方法可表示为：
[0095][0096]
式中，ir(i)表示第i轮迭代时的学习率；ir
origin
表示初始设定的学习率；r
decay
指代衰减率系数，取值在[0,1]之间；i代表当前迭代所处的轮次；c
epoch
表示固定衰减步长。
[0097]
可见每过一个固定衰减步长c
epoch
学习率就下降为此前学习率的r
decay
倍，从而实现学习率的率先，优化训练过程。
[0098]
实施例四：
[0099]
步骤5中，将训练集中的训练样本分成若干个批次并按批次送入负荷预测模型中进行训练，采取余弦退火衰减学习率调整的方法优化训练过程，并用验证集对负荷预测模型的超参数进行调整直至收敛，用调整后的负荷预测模型进行区域电力负荷预测。
[0100]
该实施例考虑了学习率对预测模型训练的影响，引入余弦退火衰减学习率调整的方法优化训练过程，余弦退火衰减学习率调整方法可表示为：
[0101][0102]
式中，ir
i
(t
cur
)表示当前的学习率；ir
max
与ir
min
分别指代学习率设置的最大值、最小值； t
cur
表示当前执行到了第t
cur
个epoch；t
i
代表在第i轮训练中的最大epoch数。
[0103]
可见在每一轮训练过程中学习都以余弦的形式在最大值与最小值之间往返变化，一方面可以加速训练过程的收敛，另一方面也可以避免陷入局部最优。
[0104]
显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。