基于多点位测量的零件全场位移感知方法与流程

1.本发明涉及空间测量技术领域，具体涉及一种基于多点位测量的零件全场位移感知方法。


背景技术：

2.随着飞机制造业的高速发展，飞机装配过程的智能化已是必然趋势，对飞机装配过程中零件的点位信息等状态数据的测量精度与实效性要求也越来越高。工装作为飞机装配的精度基准，其关键零件的全场位移信息的在线高精高效获取至关重要，直接影响飞机的装配精度与装配质量。由于飞机工装零件结构多样、装配过程工况复杂等苛刻的测量环境，导致测量空间与测量手段严重受限，使得精度与实效性双重高要求的测量难度成倍增加。


技术实现要素：

3.本发明的目的在于，提供一种基于多点位测量的零件全场位移感知方法，其中，所述零件为三维物体并且为刚性的，所述方法包括以下步骤：
4.步骤一：在所述零件实体的表面上选取m个测量点位，测量所述m个测量点位在所述零件处于第一位置时的坐标，并得到零件坐标其中，其中，≥5；
5.步骤二：建立所述零件的数学模型，在该数学模型上确定与所述m个测量点位的位置对应的m个模型点位，并获取所述m个模型点位的模型坐标其中，
6.步骤三：计算所述模型坐标到所述零件坐标的旋转平移矩阵r1t1；
7.步骤四：测量所述m个测量点位在所述零件处于第二位置时的坐标，并得到零件坐标其中，
8.步骤五：计算所述模型坐标到所述零件坐标的旋转平移矩阵r2t2；
9.步骤六：基于r1t1和r2t2获得所述零件从所述第一位置到所述第二位置的位移。
10.在一种实施方式中，通过以下步骤确定m的最小值：
11.步骤i：在所述零件的数学模型中，基于所述m个模型点位处的平面方程将所述模型坐标变换为如下形式：
12.13.其中，平面方程表示为：
[0014][0015]
步骤ii：计算所述m个模型点位中每两点之间的距离矢量组成的距离矢量矩阵dm：
[0016][0017]
其中，每列元素表示两个模型点位之间的距离矢量，距离矢量矩阵dm的总列数为r＝(m-1)+(m-2)
…
+2+1＝m(m-1)/2，
[0018]
步骤iii：计算所述m个测量点位中每两点之间的距离矢量组成的距离矢量矩阵dc：
[0019][0020]
步骤iv：将所述m个测量点位中每两点之间的距离与所述m个模型点位中每两点之间的距离一一对应相等作为求解以下公式的约束条件，并由此基于以下公式获得测量点位数量m的最小值为5：
[0021][0022]
在一种实施方式中，在所述步骤一中，基于所确定的m的最小值选取测量点位。
[0023]
在一种实施方式中，计算所述模型坐标到所述零件坐标的旋转平移矩阵rt包括以下步骤：
[0024]
步骤a：计算和的均值矩阵ac和am：
[0025][0026][0027]
步骤b：计算和与其各自均值矩阵ac和am的差值矩阵lc和
[0028]
lm：
[0029][0030][0031]
步骤c：计算差值矩阵lc和lm的乘积h：
[0032][0033]
步骤d：将h进行奇异值分解，得到h＝usv：
[0034]
[u,s,v]＝svd(h)
[0035]
步骤e：计算旋转平移矩阵rt：
[0036]
r＝vu
t
[0037]
t＝a
c-ram[0038]
计算得到m个模型点位到m个测量点位的映射关系：
[0039]
pc＝rpm+t
[0040]
在一种实施方式中，所述方法还包括以下步骤：基于所述步骤e得到的所述映射关系，获得所述零件上的所有点位qc与所述零件的数学模型上的所有点位qm之间的映射关系：
[0041]
qc＝rqm+t
[0042]
在一种实施方式中，基于r1t1和r2t2获得所述零件从所述第一位置到所述第二位置的位移包括以下步骤：
[0043]
步骤i：获得所述零件在所述第一位置时与所述零件的数学模型的映射关系为：
[0044][0045]
其中，表示所述零件在第一位置时所有点位的坐标，
[0046]
步骤ii：获得所述零件在所述第二位置时与所述零件的数学模型的映射关系为：
[0047][0048]
其中，表示所述零件在所述第二位置时所有点位的坐标，
[0049]
步骤iii：基于步骤i的映射关系得到以下公式：
[0050][0051]
步骤iv：基于步骤ii的映射关系和步骤iii的公式得到以下公式：
[0052][0053]
根据本发明所给出的方案，能够仅通过少量的测量和计算即可快速高效实现对零件的全场位移的感知，同时，本方法通用性高，适用于各种复杂形状和结构的零件，具有广泛的应用前景。
附图说明
[0054]
为了更好地理解本发明的上述及其他目的、特征、优点和功能，可以参考附图中所示的优选实施方式。附图中相同的附图标记指代相同的部件。本领域技术人员应该理解，附图旨在示意性地阐明本发明的优选实施方式，对本发明的范围没有任何限制作用，图中各个部件并非按比例绘制。
[0055]
图1是基于多点位测量的零件全场位移感知方法所使用的测量系统的示意图。
[0056]
图2是零件的测量点位到对应的数学模型的模型点位的映射示意图。
[0057]
图3是获得的零件全场位移感知结果的示意图。
[0058]
其中：1-零件；2-相机；3-测量点位；4-零件的数学模型；5-零件的数学模型的所有点位的坐标qm；6-零件的所有点位的测量坐标qc。
具体实施方式
[0059]
零件(例如飞机的工装)在例如装配过程中，其空间位置和姿态发生变化，例如零件进行了平移移动以及发生了一定角度的旋转，这些位移信息很难直接测量得到。为此，本发明提出了一种基于多点位测量的零件全场位移感知方法，“多点位测量”是指测量零件上的多个点(也称为点位)的坐标，由于零件发生了移动(包括旋转和平移)，因此其产生了位
移，利用本发明的方法可以确定得到该位移(即“位移感知”)，而“零件全场位移”是指零件作为一个整体(包括其上的全部点位)的位移，零件移动前和移动后的位置之间可以通过位移向量表示，位移向量在三维空间内的分布情况称为位移场。
[0060]
在本发明的方法中，建立零件的数学模型，数学模型中的零件具有固定不变的空间位置和姿态，零件的位置是通过坐标(或称为坐标矩阵)表征的，零件数学模型的各个点位的坐标信息是已知的并且是恒定不变的，而零件从第一位置移动到第二位置时，其第一位置和第二位置的坐标信息是未知量并且需要测量，并且第一位置到第二位置的位移也是未知量并且无法直接测量得到；为此可以借用作为已知量的零件数学模型的位置作为媒介，首先计算出零件的第一位置到数学模型的位移向量，即得到零件的第一位置到数学模型的相对位移，然后计算出零件的第二位置到数学模型的位移向量，即得到零件的第二位置到数学模型的相对位移，最后基于这两个相对位移确定出两个位置之间的位移，即通过计算间接得到零件的位移。
[0061]
在计算中，不同位置之间的位移是通过位移向量表征的，位移向量是通过不同位置下零件的坐标矩阵之间的转换矩阵表征的并且表示不同位置之间的位移(包括旋转和平移)，转换矩阵即为本领域已知的旋转平移矩阵rt(即旋转矩阵r和平移矩阵t)。为此，测量零件在第一位置下以及第二位置下的坐标，分别计算得到这两组坐标到数学模型的两个旋转平移矩阵，通过这两个旋转平移矩阵能够确定出零件在第一位置下和第二位置之间所发生的相应旋转和平移。
[0062]
该方法具体实施时，并不是而且也没有必要测量零件的所有点位，而是测量出有限个点位的坐标即可确定这些点位到数学模型的对应点位的旋转平移矩阵，而零件的所有点位与数学模型的点位之间均满足所得到的旋转平移矩阵。在下文中，要测量的零件上的点位称为测量点位，零件数学模型上与测量点位的位置对应的点位称为模型点位，测量得到的测量点位的坐标称为零件坐标，模型点位的坐标称为模型坐标。
[0063]
设定需要测量m个测量点位，其坐标表示为零件坐标pc或(i＝(1,2,
…
,m))，所对应的数学模型的m个模型点位的坐标表示为模型坐标pm或以零件为三维零件(即三维物体)为例，m个测量点位的坐标为m个模型点位的坐标为在本文中，为了便于表达和描述，坐标pm或除了表示具体的坐标以外，本身也可以用于表示第i个模型点位，这同样适用于pc或以及下文描述的qc和qm。
[0064]
在测量时，由于只能测量零件实体的外表面上的点，内部的点无法测量，因此将m个测量点位布设于零件的表面上，即在零件实体的表面上选取m个测量点位，在对应地，m个模型点位也位于数学模型的外表面上。
[0065]
概括来讲，本发明的方法包括以下步骤：
[0066]
步骤一：在零件实体的表面上选取m个测量点位，测量所述m个测量点位在零件处于第一位置时的坐标，并得到零件坐标其中，
[0067]
步骤二：建立零件的数学模型，在该数学模型上确定与所述m个测量点位的位置对应的m个模型点位，并获取所述m个模型点位的模型坐标其中，
[0068]
步骤三：计算模型坐标到所述零件坐标的旋转平移矩阵r1t1；
[0069]
步骤四：测量所述m个测量点位在零件处于第二位置时的坐标，并得到零件坐标其中，
[0070]
步骤五：计算模型坐标到所述零件坐标的旋转平移矩阵r2t2；
[0071]
步骤六：基于r1t1和r2t2获得所述零件从第一位置到第二位置的位移。
[0072]
下面确定需要测量的m个点位的最少数量，所基于的构思是，零件为刚性的，不产生变形，在零件移动前后的各个位置处，零件上两点之间的距离是恒定不变的，并且m个测量点位中每两点之间的距离与m个模型点位中每两点之间的距离一一对应相等。在计算中，每两点之间的坐标的差值组成一个距离矢量，通过该距离矢量可以计算出这两个点位之间的距离，所有这些距离矢量组成一个距离矢量矩阵，该距离矢量矩阵包含并表征每两个点位之间的全部数量的距离，下面通过以下步骤确定m的最小值。
[0073]
步骤i：基于零件的数学模型，将m个模型点位的模型坐标变换为新的坐标形式，以便于计算m个模型点位的距离矢量以及距离矢量矩阵。
[0074]
在数学模型中，如上所述，m个模型点位位于零件数学模型的表面上，一种情况是这些表面为平面，则这些表面在数学模型中具有平面方程这些方程是已知的并且可以从数学模型中获取；此外，也存在外表面为曲面的情况，此时，取数学模型在模型点位处的切平面的平面方程，并且这些平面方程在数学模型的坐标系中也是已知的、可以直接获得，下文中将这两种情况下的平面方程统一用表示，并且模型点位符合这些方程，即在数学上存在以下关系：
[0075][0076]
一般性地，可以从零件的数学模型中获得表示为如下公式(1)：
[0077][0078]
其中，ak、bk、ck、dk表示平面方程的系数，
[0079]
将m个模型点位的坐标代入公式(1)中，将其坐标值变换为如下形式：
[0080]
[0081][0082]
…
[0083][0084]
其中，ai→k、bi→k、ci→k、di→k表示在第k个平面上的模型点位的平面方程的系数，以为例，a2→k、b2→k、c2→k、d2→k表示在第k个平面上的模型点位的平面方程的系数。
[0085]
对于坐标变换后的形式，其由两个坐标xi和yi表征，未知量的数量由原来的3个(即xi、yi、zi)变成2个。
[0086]
步骤ii：计算m个模型点位中每两点之间的距离矢量组成的距离矢量矩阵dm，表示为如下公式(2)：
[0087][0088]
其中，每列元素表示两个模型点位之间的距离矢量，距离矢量包括这两个点位之间的坐标值之间的差，一共有3个数值，即x坐标之间的差值、y坐标之间的差值以及z坐标之间的差值，通过此距离矢量可以计算出这两个点位之间的距离。
[0089]
如公式(2)所表示的，距离矢量矩阵dm的总列数(即距离矢量的总数量或者点之间的距离的总数量)为r＝(m-1)+(m-2)
…
+2+1＝m(m-1)/2。
[0090]
步骤iii：类似地，计算m个测量点位中每两点之间的距离矢量组成距离矢量矩阵dc，表示为如下公式(3)：
[0091][0092]
步骤iv：由于零件为刚性的，因此在零件与其数学模型之间，对应点之间的距离一一对应地相等，即，如下公式(4)所示：
[0093][0094]
公式(4)成立，即有解，根据上文描述，dc由测量点位pc的坐标计算得到，dm中的未知量为(xi,yi),i＝(1,2,
…
,m)，共2m个未知量，约束条件为r＝m(m-1)/2，因此要求约束条件的数量大于等于未知量的数量，即如下公式(5)所示：
[0095]
m(m-1)/2≥2m
ꢀꢀ
(5)
[0096]
求解公式(5)，得到m≥5，即对于三维零件而言，最少需要测量5个点即可实施本发明的方法。
[0097]
类似地，对于二维零件(即平面零件，例如板件)而言，其由两个坐标xy表征，坐标信息为同样利用上述方法计算得到m≥3，即对于二维零件而言，最少需要测量3个点即可实施本发明的方法。
[0098]
计算旋转平移矩阵rt包括以下步骤：
[0099]
步骤a：计算pc和pm的均值矩阵ac和am，其中，均值矩阵是指这些测量点位的相应坐标值的平均值(即这些测量点位的x坐标的平均值、y坐标的平均值以及z坐标的平均值)组成的矩阵，如下公式(6)和(7)所示：
[0100][0101][0102]
步骤b：计算pc和pm与其各自均值矩阵ac和am的差值矩阵lc和lm，差值矩阵是指这些测量点位的相应坐标值与其均值矩阵的相应坐标值(即x坐标值、y坐标值以及z坐标值)之间的差组成的矩阵，如下公式(8)和(9)所示：
[0103]
lc＝p
c-acꢀꢀ
(8)
[0104]
lm＝p
m-amꢀꢀ
(9)
[0105]
步骤c：计算差值矩阵lc和lm的乘积h，如下公式(10)所示：
[0106][0107]
步骤d：将h进行svd分解(即奇异值分解)，得到h＝usv，如下公式(11)所示：
[0108]
[u,s,v]＝svd(h)
ꢀꢀ
(11)
[0109]
步骤e：根据上述svd分解结果，计算旋转平移矩阵rt，如下公式(12)和(13)所示：
[0110]
r＝vu
t
ꢀꢀ
(12)
[0111]
t＝a
c-ramꢀꢀ
(13)
[0112]
得到旋转平移矩阵rt，即可得到这m个模型点位到m个测量点位的映射关系，即二者之间的位移向量，如下公式(14)所示：
[0113]
pc＝rpm+t
ꢀꢀ
(14)
[0114]
将这m个点位扩大到整个零件，即零件上的所有点位qc以及数学模型上所有点位qm均满足公式(14)，因此最终得到如下公式(15)：
[0115]
qc＝rqm+t
ꢀꢀ
(15)
[0116]
公式(15)即表征零件与其数学模型之间的零件全场位移。
[0117]
利用上述计算旋转平移矩阵rt的方法，计算出零件在第一位置时与零件的数学模型之间的旋转平移矩阵r1和t1，得到二者之间的映射关系，如以下公式(16)所示：
[0118][0119]
其中，表示零件在第一位置时所有点位的坐标。
[0120]
类似地，计算得到零件在第一位置时与零件的数学模型之间的旋转平移矩阵r2和t2，得到二者之间的映射关系，如以下公式(17)所示：
[0121][0122]
其中，表示零件在第二位置时所有点位的坐标。
[0123]
由公式(16)得到以下公式(18)：
[0124][0125]
其中，(r1)-1
表示r1的逆矩阵。
[0126]
将公式(18)代入公式(17)，得到公式(19)：
[0127][0128]
由公式(19)可以得到零件所有点位与之间的映射关系，即基于r1t1和r2t2获得零件从第一位置到第二位置的位移。
[0129]
以此类推，当零件移动到第三位置时，可以计算得到零件的第三位置与第一位置或第二位置之间的位移，即感知零件各个位置之间的位移，获得零件的位移场。
[0130]
下面结合具体零件和附图详细描述本发明的具体实施方式。图1示出了三维实体零件1，其处于某个位置，零件整体为l形并且包括肋，其外轮廓包括多个平面，但这仅是本发明的简单示例，零件还可以为各种其他形状和结构并且其外轮廓也可以包括各种形状的曲面，例如二次曲面，包括球面、椭球面、圆柱曲面、双曲面等。
[0131]
图1的测量系统包括相机2，用于拍摄并测量在该位置下零件1上的各个点位的空间坐标。零件1的测量点位3布设在零件的表面上，即，相机2测量零件表面上的点位的坐标；并且这些测量点位3处于相机的视场范围内，为此，在测量之前，可以调整相机或零件的位置，使得零件上被布设测量点位的区域或位置被相机捕捉到。测量点位的位置可以随意选择，只要其位于相机的视场范围内即可，测量点位的位置确定好之后，其与零件之间的相对位置即被确定并且不再改变。
[0132]
测量点位可以选择具有明显特征的位置，例如，测量点位可以位于零件的棱边上、两个平面之间的相交线上或者是线之间的交点，如此，测量点位与零件之间的位置关系可以快速、容易地确定，与此对应地，零件的数学模型上与测量点位对应的模型点位的位置可以相应地确定，但不限于此，测量点位可以选择在各种位置，并且通过与零件的参考元素(例如，平面、线、交点)之间的距离来表征。以图1中的点位为例，其位于零件的左侧竖直平面上，与零件的顶部平面相距一定距离，并且与左侧竖直平面的左右两条棱边相距一定距离，通过以顶部平面、所述两条棱边作为参考元素，可以容易地选择并定位该点位的位置，对应地，在零件的数学模型上，如图2所示，可以同样依据上述参考元素和距离定位出对应的模型点位的位置，以此类推，可以确定所有的测量点位和模型点位的位置，进而进行后续的步骤。
[0133]
根据上文描述的位移感知方法，对于三维零件而言，至少需要测量5个点位，但也可以测量多于5个点位。如图1所示，零件上布设了5个点位为了全面反映零件的整体形状，这些点位均匀地分散布置在零件的多个平面上，其中和位于同一平面上。比较优选的是这些点位可以布置为一个点位对应地布设在一个平面上，极端的情况是这些点位可以布设在同一平面上。注意的是，图1示出了零件的外表面均为平面并在这些平面上布设测量点位的实施例，但如上所述，不限于此，零件也可以包括曲面并且测量点位布设在曲面上。根据上述方法，通过参考元素表征这些测量点位的位置，并对应地，在零件的数学模型上确定模型点位的位置，如图2所示，测量点位在数学模型上对应位置的模型点位为
[0134]
下面以这5个点位对上述方法求出的m的最小值为5进行验证。零件的数学模型建立了xyz坐标系并且其外表面的坐标信息是已知的，5个模型点位的坐标信息为这5个模型点位位于零件模型的4个表面上，其中和位于同一表面上，因此，与模型的表面存在以下关系：
[0135][0136]
如图2所示，根据数学模型的坐标信息，获取这4个表面的平面方程如下：
[0137][0138][0139][0140][0141]
因此有如下：
[0142][0143][0144][0145][0146][0147]
此处注意的是，本实施例是测量点位所布设的零件表面为平面的情况，因此点位的坐标符合平面的方程；在测量点位布设在曲面上的情况下，采用曲面在该点位的切平面的方程，即，测量点位位于该切平面上，其坐标符合该切平面的方程。
[0148]
根据零件数学模型上模型点位的关系，中每两点之间的距离矢量组成的距离矢量矩阵dm可表示为：
[0149][0150]
则矩阵dm的总列数表示点之间的距离的总数量，其大小为r＝(5-1)+(5-2)
…
+2+1＝5(5-1)/2＝10。
[0151]
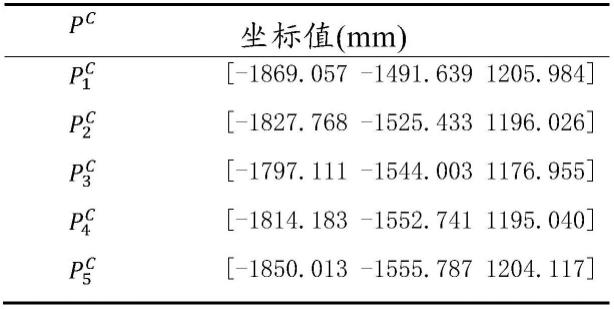
在零件的实际测量中，与5个模型点位pm对应的5个测量点位pc的测量坐标值如下表1所示。
[0152]
表1
[0153][0154]
与数学模型中模型点位的距离矢量矩阵dm对应地，测量点位pc中每两点之间的距离矢量组成的距离矢量矩阵dc可根据表1计算求得：
[0155][0156]
由于零件为刚性的，因此每两点之间距离恒定，并且在零件与其数学模型之间，对应点之间的距离一一对应地相等，则有
[0157][0158]
该公式成立，根据以上推导可知，dm中未知量为10个，dc由表1的5个测量点位pc计算获得，即约束条件为10个，可知未知量的数量等于约束条件的数量，因此该公式有解，从而验证了本发明的方法中最少测量m＝5个点。
[0159]
接下来，确定零件在图2所示的位置下，测量点位pc到模型点位pm的映射关系，即确定二者的坐标矩阵之间的转换矩阵、即旋转平移矩阵rt。
[0160]
根据数学模型的坐标信息，5个模型点位pm的坐标值如下表2所示：
[0161]
表2
[0162][0163][0164]
首先，计算pc和pm的均值矩阵ac和am，如下：
[0165][0166]
[0167]
然后，计算pc和pm与其各自均值矩阵ac和am的差值矩阵lc和lm，如下：
[0168][0169][0170]
接下来，计算lc和lm的乘积h，即令
[0171][0172]
然后，将h进行svd分解(即奇异值分解)，即h＝usv，得到如下
[0173][0174][0175][0176]
根据上述计算结果，计算旋转平移矩阵rt如下：
[0177][0178]
t＝a
c-ram＝[-1815.161
ꢀ‑
1611.369 1293.901]
t
[0179]
最后，得到模型点位pm到测量点位pc的映射关系，表示为：
[0180]
pc＝rpm+t
[0181]
其数学意义为，模型点位pm通过旋转向量(即旋转矩阵r)和平移向量(即平移矩阵t)变换到测量点位pc，具体到零件，其物理意义为，零件数学模型上的点位pm经过与旋转矩阵r相关的旋转和与平移矩阵t相关的平移移动到测量点位pc，而所经历的旋转角度和平移距离可以分别通过旋转矩阵r和平移矩阵t来表征和确定，具体计算方法是本领域已知的，在此不再赘述。
[0182]
将这有限的5个离散点扩展到整个零件，如上所述，零件的所有点位qc与其数学模型的所有点位qm之间均满足上述关系，即
[0183]
qc＝rqm+t
[0184]
具体如图3所示，左侧的标号5表示零件的数学模型的所有点位qm的坐标，而右侧的标号6表示零件的所有点位qc的测量坐标，二者具有不同的坐标值、具有不同的位置和姿
态，二者之间的位移(包括旋转和平移)由旋转矩阵r和平移矩阵t来表征和确定。
[0185]
图1至图3具体描绘了如何确定零件在某一个位置下与零件的数学模型之间的位置映射关系。在零件每次移动时，例如将零件移动前位置定义为第一位置，将零件移动后的位置定位为第二位置，如上所述利用本发明的方法，可以仅通过测量零件实体上的5个点位在移动前和移动后的坐标，即可最终得到如公式(19)所表征的位移，即确定零件每次移动的位移，实现对零件全场位移的感知。
[0186][0187]
通过感知零件每次移动的位移，获得零件的位移场，建立位移场后可以将零件在空间中的点位用位移场的坐标信息表示，实现整个零件的数字化建模，便于开展零件的空间坐标及矢量位移(包含平移及旋转)测量。
[0188]
本发明的方法过程简单，易于实现，消耗的资源少，仅通过少量的测量和计算即可快速高效完成对零件的全场位移的感知，同时，本方法通用性高，适用于各种复杂形状和结构的零件，具有广泛的应用前景。
[0189]
本发明的多种实施方式的以上描述出于描述的目的提供给相关领域的一个普通技术人员。不意图将本发明排他或局限于单个公开的实施方式。如上所述，以上教导的领域中的普通技术人员将明白本发明的多种替代和变型。因此，虽然具体描述了一些替代实施方式，本领域普通技术人员将明白或相对容易地开发其他实施方式。本发明旨在包括这里描述的本发明的所有替代、改型和变型，以及落入以上描述的本发明的精神和范围内的其他实施方式。