一种基于FLAC3D-Python二次开发的边坡地震可靠度快速计算方法

一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法
技术领域
1.本发明涉及边坡工程风险评估领域，具体一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法。


背景技术：

2.我国是一个地震灾害频发的国家。地震荷载引发的山体滑坡等自然灾害，会对人类生命财产造成巨大伤害。面对大量的边坡灾害隐患，从防灾减灾的角度进行考虑，需要对边坡在地震作用下的稳定性和失稳后的影响进行评估。
3.现有技术对边坡地震性能评估和概率分析时往往非常复杂和耗时，需要建立一种快速准确的边坡位移和失效概率计算模型；对边坡的抗震性能评估多基于边坡的抗震设计规范，即在边坡加固设计中考虑地震烈度的影响；对准确的边坡土性参数需要进行勘察才能得到，同时地震时程和地震宏观量值如地震峰值加速度均具有不确定性，缺少对地震动随机性和土性参数不确定性条件下的天然边坡地震失效概率评估，传统的概率分析方法多以蒙特卡洛模拟(mcs)为基础来分析边坡永久位移的概率特征，计算复杂且耗时，目前已有部分发明开展提高计算效率的工作。《一种边坡强度折减系数多线程并行计算方法》(申请号201711353469.3)，提出了一种多线程并行计算方法，提高了边坡强度折减法计算的效率，但是该方法只是将计算强度折减系数过程中的迭代步数进行了减少，无法应用到地震动随机性和土性参数不确定性分析中。


技术实现要素：

4.本发明所要解决的技术问题是，提供了一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法，避免缺少对地震动随机性和土性参数不确定性条件下的天然边坡地震失效概率评估的缺陷，克服现有技术由于土体参数不确定和地震动随机性难以模拟的缺陷，通过拟静力分析和动力时程分析两种方法，分别以安全系数和永久位移作为边坡失稳判据，并分别通过一阶可靠度迭代算式工程可靠度迭代算法和改进的工程可靠度迭代算法计算可靠度指标，能够迅速可靠地判断边坡地震稳定性，为相关工程人员提供了一种有效的评判手段。
5.为解决上述技术问题，本发明采用的技术方案为：
6.一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法，其特征在于，建立强度折减拟静力分析模型和动力时程分析非线性耦合模型，强度折减拟静力分析模型采用工程可靠度迭代算法求解地震荷载下的可靠度指标，动力时程分析非线性耦合模型采用改进的工程可靠度迭代算法快速求解地震荷载下的可靠度指标。
7.进一步的，工程可靠度迭代算法通过固定迭代步长求解不同拟静力地震动系数下边坡不同破坏模式下的可靠度指标。
8.工程可靠度迭代算法的计算公式为：
[0009][0010]
g(x)＝f
s
‑1ꢀꢀꢀ
(2)
[0011][0012][0013]
其中：此处x
k
是强度折减拟静力分析模型中第k步迭代包含随机变量的向量，x
k
＝[x1,x2,x3]，x1为边坡的黏聚力数值，x2为边坡的内摩擦角数值，x3为地震荷载的大小；x
k+1
是强度折减拟静力分析模型中第k+1步迭代包含随机变量的向量；为在第k步迭代点的修正后的相关矩阵，r是强度折减拟静力分析模型的相关矩阵，由矩阵各列间的相关系数构成，是第k步的标准差；g(x)是极限状态函数，等于0时为极限状态，在拟静力分析模块中g(x)＝f
s
‑
1，f
s
是安全系数；是强度折减拟静力分析模型第k步迭代的等效正态均值矩阵；β是强度折减拟静力分析模型的地震可靠度指标；是强度折减拟静力分析模型初始随机变量空间的第i步计算得到的设计点值；和分别是强度折减拟静力分析模型第i步的等效正态均值和等效标准差。
[0014]
进一步的，强度折减拟静力分析模型包括以下步骤：
[0015]
步骤(ⅰ)：在初始变量空间下选择初始迭代点x
k
来求极限状态函数g(x
k
)；
[0016]
步骤(ⅱ)：将矩阵x
k
中第一个值x
k,1
微小变化x
k,1
+δx1，其余随机变量值不变，计算新的极限状态函数值g(x
k，1
)和其差值δg(x
k，1
)＝g(x
k，1
)
‑
g(x
k)
，得到差分值δg(x
k，1
)/δx1；
[0017]
步骤(ⅲ)：对于矩阵x
k
中每个随机变量x
i
重复步骤(ⅱ)，得到梯度值
[0018]
步骤(ⅳ)：拟静力分析模块对应公式(1)、(2)、(3)、(4)计算x
k+1
和β
k+1
，此时x
k+1
为设计点值；
[0019]
步骤(
ⅴ
)：当||x
k+1
‑
x||≤ε1与|g(x
k+1
)|≤ε2都满足时，结束计算，其中，ε1，ε2是任意小的实数，输出可靠度指标β。
[0020]
进一步的，改进的工程可靠度迭代算法通过变化步长迭代求解中特定边坡地震位移阈值d
c
下的可靠度指标。
[0021]
改进的工程可靠度迭代算法的计算公式为：
[0022][0023][0024]
g(x')＝d(x')
‑
d
c
ꢀꢀꢀ
(7)
[0025][0026]
[0027]
其中：此处x'
k
是动力时程分析非线性耦合模型中第k步迭代包含随机变量的向量，x'
k
＝[x'1,x'2,x'3,x'4,x'5]，x'1为上层土边坡的粘聚力数值，x'2为上层土边坡的内摩擦角数值，x'3为下层土边坡的粘聚力数值，x'4为下层土边坡的内摩擦角数值，x'5为地震动时程的峰值加速度；λ
k
和分别为定义在初始随机变量空间中的步长和搜索方向；为动力时程分析非线性耦合模型在第k步迭代点的修正后的相关矩阵，r’是动力时程分析非线性耦合模型的相关矩阵，由矩阵各列间的相关系数构成；是动力时程分析非线性耦合模型第k步迭代的等效正态均值矩阵；动力时程分析模块中，d(x')为在动力时程分析中的位移，d
c
是边坡容许位移；β'是动力时程分析非线性耦合模型的地震可靠度指标；是动力时程分析非线性耦合模型初始随机变量空间的第i步计算得到的设计点值；和分别是动力时程分析非线性耦合模型第i步的等效正态均值和等效标准差。
[0028]
其中，动力时程分析非线性耦合模型包括以下步骤：
[0029]
步骤(a)：在初始变量空间下选择初始迭代点x’k
来求极限状态函数g(x’k)
；
[0030]
步骤(b)：将矩阵x’k
中第一个值x’k,1
微小变化x’k,1
+δx1，其余随机变量值不变，计算新的极限状态函数值g(x’k，1
)和其差值δg(x’k，1
)＝g(x’k，1
)
‑
g(x’k
)，得到差分值δg(x’k，1
)/δx
’1；
[0031]
步骤(c)：对于矩阵x’k
中每个随机变量x’i
重复步骤(b)，得到梯度值
[0032]
步骤(d)：动力时程分析模块对应公式(5)、(6)、(7)、(8)、(9)计算x’k+1
和β’k+1
，此时x’k+1
为设计点值；
[0033]
步骤(e)：当||x’k+1
‑
x’||≤ε
’1与|g(x’k+1
)|≤ε
’2都满足时，结束计算，其中，ε
’1，ε
’2是任意小的实数，输出可靠度指标β’。
[0034]
优选的，强度折减拟静力分析模型具有有明确的失稳判别标准，适用于在边坡设计的初步评估。
[0035]
优选的，动力时程分析非线性耦合模型适用于边坡设计的深入评估，以及强度折减拟静力分析模型不适用的不满足收敛的情形。
[0036]
本发明的有益效果包括：
[0037]
本发明所要解决的技术问题是，提供了一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法，避免缺少对地震动随机性和土性参数不确定性条件下的天然边坡地震失效概率评估的缺陷，克服现有技术由于土体参数不确定和地震动随机性难以模拟的缺陷，通过拟静力分析和动力时程分析两种方法，分别以安全系数和永久位移作为边坡失稳判据，并分别通过一阶可靠度迭代算式工程可靠度迭代算法和改进的工程可靠度迭代算法计算可靠度指标，能够迅速可靠地判断边坡地震稳定性，为相关工程人员提供了一种有效的评判手段。
[0038]
(1)本发明以安全系数为边坡失稳判据的拟静力分析方法可以简单迅速的获取边坡地震可靠度指标，进行边坡地震的可靠度设计。
[0039]
(2)本发明以永久位移为边坡失稳判据的非线性耦合分析方法，考虑了地震动时程的不确定性和土体动力参数的不确定性，有效地求解出边坡地震的可靠度指标，较为真实的反映出地震响应下的边坡稳定性，避免得到较为保守的结果。
[0040]
(3)本发明将数值软件flac3d与python二次开发算法结合，可以较为真实地模拟土体动力特性，大变形特性等实际情况，通过较少的计算步骤得到边坡地震可靠度，便于工程人员及时掌握边坡抗震稳定性。
附图说明
[0041]
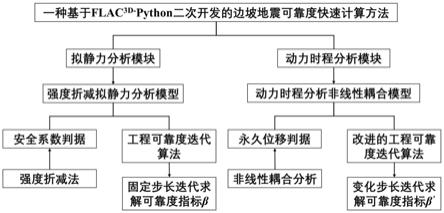
图1为本发明主要包含的内容框架；
[0042]
图2为强度折减拟静力分析流程图；
[0043]
图3为动力时程分析流程图；
[0044]
图4为flac3d与极限平衡法可靠度指标对比；
[0045]
图5为不同永久位移阈值下的可靠度指标。
具体实施方式
[0046]
下面结合附图以及具体实施例对本发明一种适用于悬挂式深基坑工程的土体参数反演分析方法作进一步详细说明。
[0047]
本发明包括拟静力强度折减分析模块和动力时程分析模块两种分析模块。拟静力分析模块和动力时程模块是针对边坡地震分析的两个不同的方法。拟静力分析假定地震荷载为大小方向不变的水平力，计算拟静力和重力共同作用下的边坡安全系数来反映边坡地震响应下的稳定性，其中安全系数通过强度折减方法进行表示。拟静力分析模块具有有明确的失稳判别标准，在初步评估和快速计算地震作用下的边坡稳定性有显著优势，适用于在边坡设计时进行一个大致的评估。但其对土体的动力特性和地震的动力效应做了一定的简化，忽略了土体的动力参数和地震动的时程特性如频率和持时等。动力时程分析模块在newmark刚性滑块基础上同时求解边坡的动力响应和滑面上的永久位移并考虑土体的非线性特征(土体剪应变增大，土体阻尼比增大而剪切模量降低)，可以考虑地震动的时程特性，适用于对重点边坡工程进行深化设计。拟静力分析模块与动力时程分析模块相辅相成，评价手段相互补充。拟静力分析模块得到的结果为：安全系数以及基于安全系数的可靠度指标；动力时程分析模块得到的结果为：永久位移以及基于永久位移位移的可靠度指标。
[0048]
传统的边坡稳定设计方法把不确定因素归结到安全系数上，但计算结果往往与实际相差甚远，甚至安全系数大者，安全程度反而低，安全系数无法成为安全程度的唯一衡量标准。因此本发明以确定性的边坡滑块分析方法为基础，计算不确定性的边坡地震可靠度指标更能反映出边坡在地震作用下的真实响应。在独立标准正态空间中对极限状态函数进行一次泰勒近似展开后得到的可靠度可看成真实可靠度的一次近似，称为一阶可靠度方法，实现一阶可靠度计算的关键是能够快速准确地搜索到极限状态函数的设计点。
[0049]
但对于某些地震作用下的动力问题工程可靠度迭代算法未必收敛，本发明通过引入变化步长后，得到改进的改进的工程可靠度迭代算法实现了迭代算法的稳定。本发明动力时程分析模块通过变化步长的改进的工程可靠度迭代算法迭代求解非线性耦合动力时程中特定边坡位移阈值dc下的可靠度指标β。随机地震动通过flac3d
‑
python二次开发，生成随机地震动时程样本，边坡二维随机场模型，并赋值给flac3d数值模型进行求解计算，能够反映土体抗剪强度参数和土体动力参数不确定性对边坡抗震性能的影响，便于实际工程人员有效评估边坡地震稳定性。
[0050]
如图1所示，一种基于flac3d
‑
python二次开发的边坡地震可靠度快速计算方法包括建立强度折减拟静力分析模型和动力时程分析非线性耦合模型，并分别通过工程可靠度迭代算法求解拟静力情况下的可靠度指标以及通过改进后的改进的工程可靠度迭代算法求解特定边坡容许位移条件下的可靠度指标。具体步骤为：
[0051]
拟静力分析模块即将地震荷载简化为拟静力系数与土体重度乘积的拟静力荷载，水平施加在边坡土体上，通过强度折减方法计算拟静力荷载下的边坡安全系数，以及通过工程可靠度迭代算法快速求解可靠度指标。flac3d通过python二次开发一阶可靠度迭代算式工程可靠度迭代算法求解可靠度指标的流程(如图2所示)如下：
[0052]
(1)首先在flac3d完成边坡建模。
[0053]
(2)输入随机变量x
k
。本发明一优选实例中x
k
＝[x1,x2,x3]，x1为边坡的黏聚力数值，x2为边坡的内摩擦角数值，x3为地震荷载的大小，x
k
＝[5.30,23.0,
‑
2.14]，x
k+1
＝[5.30,23.0,0.035]，初始k
h
＝0.035。
[0054]
(3)计算极限状态函数：
[0055]
g(x
k
)＝f
s
‑1[0056]
其中：f
s
是安全系数。
[0057]
(4)计算第k步迭代的等效正态矩阵和等效正态标准差矩阵
[0058]
本发明一优选实例为：
[0059]
μ
k
＝[μ1,μ2,μ3]＝[5.30,23.0,
‑
2.14],
[0060]
σ
k
＝[σ1,σ2,σ3]＝[5.30*0.3,23.0*0.2,0.035]
[0061][0062][0063]
(5)计算三个变量的梯度向量，采用差分形式的偏导值来计算梯度向量，可以表示为：
[0064][0065]
其中：δx
k,i
是对变量x
k,i
的一个微小扰动值，δg(x
k
)是由δx
k,i
引起的g(x
k
)差值。本发明一优选实例为：δx
k,i
＝(δx
k,1
,δx
k,2
,δx
k,3
)＝(1.00,0.20,0.02)
[0066][0067]
(6)输入相关矩阵，本发明一优选实例为：r＝[[1,
‑
0.2,0],[
‑
0.2,1,0],[0,0,1]]。并通过固定步长的迭代算法计算输入的x
k+1
：
[0068][0069]
此处x
k
是强度折减拟静力分析模型中第k步迭代包含随机变量的向量，x
k
＝[x1,x2,x3]，x1为边坡的黏聚力数值，x2为边坡的内摩擦角数值，x3为地震荷载的大小；x
k+1
是第k+1步迭代时的向量；为在第k步迭代点的修正后的相关矩阵；为梯度向量值。本发明一优选实例为：
[0070]
x
k+1
＝[4.96675365,22.61916824,0.14491666]。
[0071]
(7)当前后两步对应的随机变量向量误差和极限状态函数绝对值均小于界限时，(本发明一优选实例取ε1＝0.5，ε2＝0.05)，停止迭代，输出最终可靠度指标β。
[0072][0073]
其中：和分别是第i步的等效正态均值和等效标准差；是第k步迭代的等效正态均值向量；是初始随机变量空间(x空间)的第i步计算得到的设计点值；r是相关矩阵，由矩阵各列间的相关系数构成。
[0074]
本发明一优选实例为：
[0075]
β＝1.66636648893。
[0076]
(8)当前后两步对应的随机变量向量误差大于界限时，继续赋值迭代，直至小于等于误差限。
[0077]
本发明进行了不同拟静力地震动系数下的浅层滑动(破坏模式
‑
1)和深层滑动破坏(破坏模式
‑
2)的试算，如表1所示。可以看出两种破坏模式下的可靠度指标都随着水平地震动系数的增大而下降，而浅层滑动破坏下降是线性的，可靠度指标随拟静力荷载变化幅度较小，深层滑动破坏下降是非线性的，可靠度指标随拟静力荷载变化幅度较大。如图4所示，拟静力分析
‑
强度折减模型结合flac3d软件进行求解得到的结果与传统极限平衡法(条分法)的对比相差不大，以上两者均说明本方法具有一定的评估边坡地震稳定性的能力。
[0078]
表1不同拟静力地震动系数下的两种破坏模式的可靠度指标
[0079][0080]
动力时程分析中利用flac3d的完全非线性耦合特点，通过6.00版本中的python二次开发提供的向量计算库和数据交互接口，同时flac3d内置丰富的本构模型及自由场边界真实的反映地震荷载下的边坡应力应变模拟效果，在确定性分析的基础上进一步结合改进的工程可靠度迭代算法求解特定永久位移阈值的可靠度指标。flac3d通过python二次开发改进的工程可靠度迭代算法计算容许位移下的边坡动力可靠度指标的流程(如图3所示)如下：
[0081]
(1)首先在flac3d完成两层土边坡的建模。
[0082]
(2)输入随机变量x'
k
。本发明一优选实例中，x'
k
＝[x'1,x'2,x'3,x'4,x'5]，x'1其中为上层土边坡的粘聚力数值，x'2为上层土边坡的内摩擦角数值，x'3为下层土边坡的粘聚力数值，x'4为下层土边坡的内摩擦角数值，x'5为地震动时程的峰值加速度，x'
k
＝[x'1,x'2,x'3,x'4,x'5]＝[5.3,23,7.2,20，
‑
2.14]。
[0083]
(3)计算极限状态函数：
[0084]
g(x'
k
)＝d(x'
k
)
‑
d
c
[0085]
其中：动力时程分析模块中，d(x
k
')为在动力时程分析中的位移，d
c
是边坡容许位移。
[0086]
(4)计算第k步迭代的等效正态矩阵和等效正态标准差矩阵本发明一优选实例为：
[0087]
μ'
k
＝[μ'1,μ'2,μ'3,μ'4,μ'5]＝[5.3,23,7.2,20，
‑
2.14]；
[0088]
σ'
k
＝[σ'1,σ'2,σ'3,σ'4,σ'5]＝[5.3*0.3,23*0.2,7.2*0.3,20*0.2,0.35]；
[0089][0090][0091]
(5)计算五个变量的梯度向量，采用差分形式的偏导值来计算梯度向量，可以表示为：
[0092][0093]
其中：δx'
k,i
是对变量x'
k,i
的一个微小扰动值，δg(x'
k
)是由δx
k,i
引起的g(x'
k
)差值。本发明一优选实例为：
[0094]
δx'
k,i
＝(δx'
k,1
,δx'
k,2
,δx'
k,3
,δx'
k,4
,δx'
k,5
)＝(0.02,0.10,0.10,0.10,0.10)
[0095][0096]
(6)输入相关矩阵和初始步长λ＝1，利用迭代算式计算x'
k+1
和其中引入变化步长对原始迭代算法进行改进：
[0097][0098][0099]
其中：λ
k
和分别为定义在原始变量空间中的步长和搜索方向；此处x'
k
是动力时程分析非线性耦合模型模型中第k步迭代包含随机变量的向量；x'
k+1
是第k+1步迭代时的向量；为在第k步迭代点的修正后的相关矩阵；为梯度向量值。本发明一优选实例为：
[0100]
x'
k+1
＝[5.05307376,21.73958583,6.30432303,15.96743713,0.40607942]；
[0101]
r'＝[[1,0,0,0,0],[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1]。
[0102]
(7)通过监测函数m(x'
k+1
)来确定最优步长，计算每一次步长：
[0103][0104]
作为空间的回溯线搜索技术，利用最大步长armijo规则如下：
[0105][0106]
其中：a和b为(0,1)内规定的参数，b此处取值0.5，j为求解最优解的整数，为求监测函数的梯度向量；和分别是第i步的等效正态均值和等效标准差；是初始随机变量空间的第i步计算得到的设计点值。
[0107]
(8)若m(x'
k+1
)≥m(x'
k
)，减小步长为λ＝0.5
j
，(j为整数)。重复步骤(6)计算x'
k+1
。若m(x'
k+1
)＜m(x'
k
)继续下一步。本发明一优选实例为：m(x'
k+1
)＝0.0190494574921，m(x'
k
)＝0.0386726605367。
[0108]
(9)当前后两步对应的随机变量向量误差和极限状态函数绝对值均小于界限时，(本发明一优选实例取ε'1＝0.5，ε'2＝0.05)，停止迭代，输出最终可靠度指标β'。
[0109][0110]
其中：β'是改进的改进的工程可靠度迭代算法得到的可靠度指标；r’是相关矩阵，由矩阵各列间的相关系数构成。
[0111]
本发明一优选实例中二次开发代码为：β'＝1.124825588。
[0112]
(10)当前后两步对应的随机变量向量误差大于界限时，继续赋值迭代，直至小于等于误差限。
[0113]
非线性耦合
‑
动力时程分析模型的试算结果如5所示，相比浅层破坏的结果，深层滑动破坏的可靠度指标随着永久位移阈值呈现平缓的增大趋势。本方法在非线性耦合
‑
动力时程分析模型中仍具有一定的评估边坡地震稳定性的能力。
[0114]
在此处所提供的说明书中，说明了大量具体细节。然而，能够理解，本发明的实施例可以在没有这些具体细节的情况下被实践。在一些实例中，并未详细示出公知的方法、结构和技术，以便不模糊对本说明书的理解。
[0115]
类似地，应当理解，为了精简本公开并帮助理解各个发明方面中的一个或多个，在上面对本发明的示例性实施例的描述中，本发明的各个特征有时被一起分组到单个实施例、图、或者对其的描述中。然而，并不应将该公开的方法解释成反映如下意图：即所要求保护的本发明要求比在每个权利要求中所明确记载的特征更多特征。更确切地说，如权利要求书所反映的那样，发明方面在于少于前面公开的单个实施例的所有特征。因此，遵循具体实施方式的权利要求书由此明确地并入该具体实施方式，其中每个权利要求本身都作为本发明的单独实施例。
[0116]
如在此所使用的那样，除非另行规定，使用序数词“第一”、“第二”、“第三”等等来描述普通对象仅仅表示涉及类似对象的不同实例，并且并不意图暗示这样被描述的对象必须具有时间上、空间上、排序方面或者以任意其它方式的给定顺序。
[0117]
尽管根据有限数量的实施例描述了本发明，但是受益于上面的描述，本技术领域内的技术人员明白，在由此描述的本发明的范围内，可以设想其它实施例。此外，应当注意，本说明书中使用的语言主要是为了可读性和教导的目的而选择的，而不是为了解释或者限定本发明的主题而选择的。因此，在不偏离所附权利要求书的范围和精神的情况下，对于本技术领域的普通技术人员来说许多修改和变更都是显而易见的。对于本发明的范围，对本
发明所做的公开是说明性的，而非限制性的，本发明的范围由所附权利要求书限定。
[0118]
以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。