用于工程图纸融合的二维多元信号经验模态分解快速方法与流程

1.本发明属于工程图纸融合技术领域，具体涉及一种用于工程图纸融合的二维多元信号经验模态分解快速方法。


背景技术：

2.输变电工程中，工程图纸作为工程项目各阶段的重要依据，需妥善保存。在对工程图纸进行数字化管理的过程中，受操作不当或扫描技术等问题影响，数字化的图纸往往会呈现不同局部的模糊。如何通过这些模糊的图片得到完整清晰的工程图纸成为亟待解决的问题。
3.近些年提出来的经验模态分解(empirical mode decomposition，emd)是一种分析非线性非稳态信号的有效算法，也是希尔伯特变换的重要组成部分。该算法完全由数据驱动，可以将信号自适应地分解到多个频率空间上，得到的成分称之为本征模态函数(intrinsic mode functions，imfs)。在emd的基础之上有了许多扩展性的发展。多元经验模态分解(multivariate empirical mode decomposition，memd)通过将多元信号同时映射到不同方向上，得到多元信号的局部均值和信号包络，以此实现对多元信号的分解。二维经验模态分解(bidimensional empirical mode decomposition，bemd)将emd运用到二维信号上，通过寻找二维曲面的局部极大值和极小值，在此基础上构造均值曲面，从而实现二维信号(图像)的分解。虽然使用bemd也可以进行图像融合，但是无法保证待融合的每张图的二维本征模态函数(bidimensional intrinsic mode functions，bimfs)都分解到相同空间尺度。二维多元经验模态分解(bidimensional multivariate empirical mode decomposition，bmemd)将多元经验模态分解运用到二维图像上，实现了对不同图像在相同空间尺度上的融合，减少了图像融合时空间尺度的丢失。但bmemd的缺陷在于，通过筛选得到极小值和极大值包络的过程中，需要对二维离散数据进行曲面拟合，这会耗费较多的计算时间。
4.中国申请公布号为cn111369488a的专利公开了一种用于多图像融合的二维多元信号经验模态分解快速算法，其在bmemd的基础上提出了一种基于均值估计的快速算法(mean approximation bidimensional multivariate empirical mode decomposition，ma
‑
bmemd)，可以实现对二维多元信号的快速分解，可以快速地将多张图片分解到相同空间尺度，并在此基础上进行融合。但此专利是选取了每个信号的极值点进行均值估计，得到的有效信息可能不足；同时，此专利是采用局部方差最大法对信号进行融合，其是选取具有较大局部方差的像素值作为融合系数，融合系数选择一幅图像的系数而覆盖另一幅图像的系数，当两幅图像对应像素的局部方差相差不大时，使用此方法会丢失一部分有用信息，使融合后的图像产生失真。


技术实现要素：

5.发明目的：针对现有技术中存在的问题，本发明公开了一种用于工程图纸融合的
二维多元信号经验模态分解快速方法，能够保留更多的有效信息对多张局部模糊的工程图纸进行融合叠加，得到清晰的工程图纸。
6.技术方案：为实现上述技术目的，本发明采用如下技术方案：一种用于工程图纸融合的二维多元信号经验模态分解快速方法，其特征在于：包括如下步骤：
7.步骤a：将待融合的多张工程图纸组合成一个二维多元信号，作为基于均值估计的二维多元经验模态分解算法即ma
‑
bmemd算法的输入信号，其中每一张工程图纸即为二维多元信号中的一元二维信号；
8.步骤b：ma
‑
bmemd算法将输入信号中的每元二维信号同时分解到若干个频率空间中，得到对应的二维本征模态函数，其中将每元二维信号映射到频率空间中得到投影信号，基于投影信号得到每元二维信号的特征点，特征点包括极值点、鞍点和顶点，采用德劳内三角化对特征点进行均值估计得到均值曲面，通过均值曲面得到二维本征模态函数；
9.步骤c：使用基于改进空间频率的融合规则将不同元二维信号在同一个频率空间下的二维本征模态函数进行融合，作为融合后的工程图纸对应不同频率空间的二维本征模态函数，将融合后的不同频率空间的二维本征模态函数叠加即得到融合后的工程图纸。
10.优选地：步骤b包括如下步骤：
11.步骤b1、将输入信号中的每元二维信号投影到若干个投影方向上，得到每个投影方向上的投影信号，每个投影方向对应一个频率空间；
12.步骤b2、提取每元二维信号在每个频率空间上的投影信号的极值点和鞍点坐标，根据极值点和鞍点坐标得到每元二维信号的极值点和鞍点，每元二维信号的极值点、鞍点和顶点组成该元二维信号的特征点；
13.步骤b3、在每元二维信号的特征点的基础上构造德劳内三角，在每个德劳内三角内通过顶点计算其均值点；
14.步骤b4、使用三次样条插值对每元二维信号在每个频率空间上的所有均值点进行插值，扩充成与二维信号相同的大小，得到每元二维信号在每个频率空间上的均值曲面，从而得到输入信号在每个频率空间上的均值曲面；
15.步骤b5、将输入信号在所有频率空间上的均值曲面进行平均，得到输入信号的均值曲面；
16.输入信号减去其均值曲面得到中间参量，判断该中间参量是否满足预先设定的bimfs标准，若不满足，则将该中间参量作为输入信号，返回步骤b1，若满足，该中间参量即为步骤a的二维多元信号分解出的一个二维本征模态函数，则将均值曲面作为输入信号，返回步骤b1；
17.重复步骤b1至b5，直到提取出步骤a的二维多元信号的所有二维本征模态函数。
18.优选地：步骤b2中，投影信号的极值点为投影信号中8邻域内极大值和极小值的集合；
19.投影信号的鞍点为投影信号中满足4邻域内行最大列最小的点的集合。
20.优选地：步骤b5中，当第x次迭代运算的柯西标准差sd
x
小于事先设定的阈值时，停止迭代，柯西标准差按如下公式计算：
21.22.其中，r
x
(i,j)代表第x次迭代得到的二维本征模态函数；m、n是工程图纸的高和宽；当sd
x
小于阈值时，停止迭代。
23.优选地：步骤c包括入如下步骤：
24.步骤c1：计算每元二维信号在每个频率空间的二维本征模态函数的空间频率；
25.步骤c2：根据空间频率，将同一频率空间的所有二维信号的二维本征模态函数融合，即：
[0026][0027]
其中，表示第q个频率空间融合后的二维本征模态函数，表示第p元二维信号在第q个频率空间的二维本征模态函数，表示第p元二维信号在第q个频率空间的二维本征模态函数的空间频率，n表示二维信号的数量；
[0028]
步骤c3：将所有频率空间的融合后的二维本征模态函数进行叠加，得到融合后的工程图纸，即：
[0029][0030]
其中，表示融合后的工程图纸，m表示步骤c2中融合得到的二维本征模态函数的个数。
[0031]
有益效果：与现有技术相比，本发明具有如下有益效果：
[0032]
1、本发明在进行均值估计时，选取了极值点、鞍点以及二维图像的四个顶点，保留了边缘轮廓信息在内的工程图纸的更多有效信息，使融合效果更好；同时采用了基于空间频率的融合规则进行工程图纸融合，也能更好地提取高频信息、保留轮廓和边缘信息，使融合效果更好；
[0033]
2、本发明结合了现有技术的优点，成功将二维多元信号(多张工程图纸)同时分解到多个频率空间，并在此基础基于改进空间频率的融合规则实现了对工程图纸的融合，不会造成图像空间信息的丢失，同时可以融合后的图像具有较高的峰值信噪比、结构相似性和较低均方误差；
[0034]
3、本发明在将工程图纸分解得到多个bimfs的筛选过程中，使用了基于均值估计的快速算法，不再需要拟合极大值包络和极小值包络，通过均值估计的方法直接拟合均值包络，减少了二维空间曲面拟合次数，较大地减少了算法复杂度，提高了效率。
附图说明
[0035]
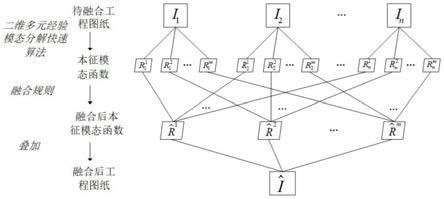
图1为本发明所述方法的流程示意图；
[0036]
图2为某次筛选过程中，使用均值估计算法计算均值点时产生的德劳内三角示意图；
[0037]
图3为通过均值估计的方法由特征点获得均值点的示意图；
[0038]
图4为左上部分模糊的工程图纸；
[0039]
图5为右上部分模糊的工程图纸；
[0040]
图6为左下部分模糊的工程图纸；
[0041]
图7为右下部分模糊的工程图纸；；
[0042]
图8为使用本发明所述方法融合出来的工程图纸；
[0043]
图9为使用bmemd融合出来的工程图纸；
[0044]
图10为理想清晰工程图纸；
[0045]
图11为专利cn111369488a中所述方法融合出来的工程图纸。
具体实施方式
[0046]
下面结合附图对本发明作更进一步的说明。
[0047]
本发明公开了一种用于工程图纸融合的二元多维信号经验模态分解快速方法，涉及二维多元信号的快速处理问题，可应用于工程图纸融合领域，可以快速将多张局部模糊的工程图纸进行融合，得到全局清晰的工程图纸。本发明基于二维多元经验模态分解，使用了一种通过均值估计得到均值曲面的近似算法，改善了经验模态分解时的效率；同时在均值估计过程中利用极值点、顶点以及鞍点来计算均值，在融合过程中采用基于改进空间频率的融合规则，能够保留更多的有效信息，提高融合后的工程图纸的质量。二维多元经验模态分解用于图像融合的主要思路是将不同的图像同时分解到不同的空间尺度，得到每张图像的二维本征模态函数(bimfs)，最后使用局部方差最大法或者局部能量最大法对相同空间尺度的bimfs进行融合。
[0048]
如图1所示，本发明所述方法包括如下步骤：
[0049]
(1)将待融合的多张局部模糊的工程图纸合成为一个二维多元信号，作为基于均值估计的二维多元经验模态分解(ma
‑
bmemd)算法的输入，其中每一张工程图纸为二维多元信号中的一元二维信号。
[0050]
(2)ma
‑
bmemd算法基于均值估计算法，将输入的二维多元信号中的每元二维信号同时分解到多个频率空间即空间尺度，即分解成多个bimfs，不同元二维信号的bimfs代表了该二维信号在特定频率空间的映射。
[0051]
将二维多元信号分解成多个bimfs，具体包括如下步骤：
[0052]
(21)确定需要融合的局部模糊的工程图纸的数目为n，频率空间即投影方向的数目为k，根据准蒙特卡洛法，生成k个单位方向矢量，其中第k个频率空间的单位方向矢量对应的角度为θ
k
。将二维多元信号i作为输入投影到这k个频率空间，分别得到投影信号其中，
[0053][0054]
其中，i
l
为二维多元信号i的第l元二维信号，为第k个频率空间的归一化的单位方向矢量，为第l元二维信号i
l
在第k个频率空间的投影信号，为二维多元信号i在第k个频率空间的投影信号。
[0055]
(22)针对二维信号i
l
在第k个频率空间的投影信号提取其局部极值点以及局
部鞍点所在坐标；
[0056]
二维信号i
l
的特征点包含三部分，即：
[0057][0058]
其中，表示二维信号i
l
位于投影信号的局部8邻域内极大值点和极小值点的集合；表示二维信号i
l
的四个顶点的集合，如果特征点都集中于二维信号内部，非常容易使得工程图纸的边缘轮廓信息缺失，使恢复出来的工程图纸边缘模糊，而四个顶点保证了工程图纸的边缘轮廓信息，将四个顶点纳入特征点，可以保证后续进行德劳内三角划分的结果充满整个二维信号的区域；表示二维信号i
l
位于投影信号的局部鞍点的集合，当前时空域的鞍点在投影后，可能是极值点，所以鞍点也包含了有效信息，如果仅仅取极值点，得到的有效信息容易不足，结合鞍点后，有效信息增多，融合的效果会更好，局部鞍点即满足4邻域内行最大列最小的点，即满足：
[0059][0060]
设二维信号i
l
的所有特征点的坐标为则特征点像素值为
[0061]
(23)通过均值估计快速算法，由二维信号i
l
的特征点得到均值点
[0062]
一种基于特征点得到近似估计均值点的快速算法，具体如下：
[0063]
使用德劳内三角化对特征点进行三角划分，得到多个特征点三角形即德劳内三角，如图2所示。对于一个特定的德劳内三角，如图3所示，假设其顶点为顶点坐标分别为和使用其重心作为一个均值点其坐标为则：
[0064][0065][0066]
其中，和均为向下取整的整数。
[0067]
均值点的像素值大小为：
[0068]
[0069]
其中，为德劳内三角的顶点的像素值；ω
p
(p＝1,2,3)表示三个顶点的权重。本发明的一种实施例中，ω
p
可以选为等权重，即
[0070][0071]
一种基于特征点得到近似估计均值点的快速算法，其算法复杂度推演如下：
[0072]
假设共有l个特征点，由l个特征点构成的德劳内三角剖分共含有2l
‑2‑
t个三角形，其中t表示位于边界上的特征点数目。因为特征点较多，可以近似忽略t，即产生2l
‑
2个德劳内三角形。使用等权重方式得到均值点的计算复杂度为：
[0073]
t
mean point
＝t
delaunay
+t
mean points computattion
[0074]
＝o(l
·
log(l))+3(2l
‑
2)(2add+1div)
[0075]
≈o(l
·
log(l))+12(l
‑
1)add
[0076]
≈o(l
·
log(l))+o(l)
[0077]
其中，t
delaunay
表示生成德劳内三角的计算复杂度，t
mean points computattion
表示由德劳内三角得到均值点的计算复杂度，add表示一次加法运算，div表示一次除法运算。
[0078]
(24)基于德劳内三角划分，使用三次样条插值对二维信号i
l
的均值点进行二维曲面插值拟合，并扩充至二维信号i
l
相同的大小，得到二维信号i
l
的投影信号的均值曲面因此可以得到二维多元信号i的投影信号的均值曲面
[0079]
本发明基于德劳内三角划分，使用三次样条插值对均值点进行插值，对二维曲面进行拟合得到均值曲面的过程，其算法复杂度为：
[0080]
t
gridfit
＝o(mn
·
log(mn))
[0081]
其中，t
gridfit
表示使用三次样条插值进行曲面拟合的复杂度；m、n分别表示二维信号每一维的长度，即图像的高和宽。
[0082]
由此可以得到基于均值估计的快速算法计算均值包络时的算法复杂度：
[0083]
t
mean approximation
＝t
mean points
+t
gridfit
[0084]
≈o(l
·
log(l))+o(l)+o(mn
·
log(mn))
[0085]
传统的bmemd计算均值曲面时，需要先计算极大值曲面和极小值曲面，其算法复杂度计算如下：
[0086]
t
envelop mean
＝t
max envelop
+t
min envelop
+t
average
[0087]
＝o(mn
·
log(mn))+o(mn
·
log(mn))+o(mn)
[0088]
其中，t
envelop mean
表示传统的bmemd算法求均值曲面的算法复杂度，t
max envelop
和t
min envelop
分别表示计算极大值和极小值曲面的算法复杂度，t
average
表示对极大值曲面和极小值曲面进行平均得到均值曲面过程的算法复杂度。
[0089]
由此可得到传统的bmemd计算均值曲面与本发明所述均值估计方法计算均值曲面的计算复杂度之差为：
[0090]
t
envelop mean
‑
t
mean approximatioan
[0091]
≈o(mn)+o(mn
·
log(mn))
‑
o(l
·
log(l))
‑
o(l)
[0092]
考虑到对于一张工程图纸，由于mn＞＞l，所以t
envelop mean
‑
t
mean approximatioan
>0，换而言之，对于单次筛选过程，本发明使用均值估计求得均值曲面的方法比传统bmemd方法计算复杂度更低。
[0093]
同时，在本发明所述方法中，由特征点得到均值点后，只需要进行一次插值扩充就可以得到均值曲面；而在传统的bmemd方法中，首先需要对极大值点进行差值扩充得到极大值曲面，再对极小值点进行差值扩充得到极小值曲面，需要进行两次插值扩充才能得到均值曲面。因此，本发明的计算效率高于传统的bmemd方法。
[0094]
(25)将k个频率空间的均值曲面进行平均作为二维多元信号i的均值曲面a，即
[0095][0096]
计算r＝i
‑
a，判断r是否满足预先设定的bimfs标准：若不满足，则将r作为输入，重复步骤(21)
‑
(25)；若满足，r即为二维多元信号i的分解出的一个bimfs，则将i
‑
r作为输入，重复步骤(21)
‑
(25)，直到所有的bimfs被提取出来。其中，步骤(21)
‑
(25)被称为一次筛选过程。
[0097]
本发明的一种实施例中采用的停止准则如下：当第x次迭代运算即筛选的柯西标准差(cauchy standard deviation，sd)sd
x
小于事先设定的阈值时，停止迭代。柯西标准差按如下公式计算：
[0098][0099]
其中，r
x
(i,j)代表第x次筛选的结果；m、n是工程图纸的高和宽；阈值一般设为0.05，当sd
x
小于阈值时，停止筛选。采用柯西标准差的停止准则，本发明所述方法能够较完整的提取出原二维多元信号i的bimfs。
[0100]
(3)在每一个频率空间，使用基于改进空间频率的融合规则将不同元二维信号的bimfs进行融合，将融合后的信号作为融合后的工程图纸对应不同频率空间的bimfs，将融合后的对应不同频率空间的bimfs叠加即可得到融合后的工程图纸。
[0101]
本发明使用基于改进空间频率的融合规则(考虑四个方向的梯度)对同一频率空间的不同元二维信号的bimfs进行融合，能更好地提取高频信息，能够更好地保留轮廓和边缘信息，具体步骤如下：
[0102]
(31)记第p元二维信号对应第q个频率空间的bimfs在位置(i,j)处的像素值大小为以(i,j)为中心，取大小为r
×
c的窗口(r、c为奇数)，计算该窗口改进后空间频率的大小为：
[0103][0104]
其中，r
f
表示水平方向的梯度：
similarity index，ssim)，计算方式分别如下：
[0120][0121]
其中，entropy表示融合后的工程图纸的图像平均信息，p
i
表示像素值为i的点占图像总像素的比率熵。
[0122][0123]
其中，sf表示融合后的工程图纸的图像空间频率(两个方向)，m、n分别是融合后的工程图纸的高和宽，i是融合后的工程图纸。
[0124][0125]
其中，rmse是融合后的工程图纸与理想工程图纸之间的均方根误差，m、n分别是融合后的工程图纸的高和宽，i是融合后的工程图纸，f是理想工程图纸。
[0126][0127]
其中，
[0128][0129][0130]
corr是融合后的工程图纸与理想工程图纸之间的互相关系数，μ
i
和μ
f
分别表示融合后的工程图纸和理想工程图纸的均值，m、n分别是融合后的工程图纸的高和宽，i是融合后的工程图纸，f是理想工程图纸。
[0131][0132]
其中，
[0133][0134]
psnr是融合后的工程图纸的峰值信噪比，mse表示融合后的工程图纸和理想工程图纸的均方误差，m、n分别是融合后的工程图纸的高和宽，i是融合后的工程图纸，f是理想工程图纸。
[0135][0136]
其中，
[0137][0138][0139][0140]
ssim是融合后的工程图纸的结构相似性，通常取c1＝(k1×
l)2，c2＝(k2×
l)2，一般的，k1＝0.01,k2＝0.03,l＝255，μ
i
、μ
f
分别表示融合后的工程图纸i和理想工程图纸f的均值，σ
i
、σ
f
分别表示融合后的工程图纸i和理想工程图纸f的方差，σ
i
σ
f
表示融合后的工程图纸i和理想工程图纸f的协方差。
[0141]
如表1所示为现有技术融合多张局部模糊工程图纸效果与本发明所述方法和专利cn111369488a中所述方法和现有的bmemd方法融合多幅工程图纸的融合效果的定量评价指标表。
[0142]
表1
[0143][0144]
对比可发现本发明所述方法融合后的工程图纸和理想工程图纸有相近的信息熵和空间频率信息，对比现有的bmemd方法和专利cn111369488a中所述方法，本发明所述方法融合后的工程图纸在均方误差、峰值信噪比及结构相似性上都优于现有的bmemd方法，同时相比于现有的bmemd方法在单次筛选时间上也极大地提升了运算效率，且与专利cn111369488a中所述方法在单次筛选时间上相差不大，体现了本发明所述方法在工程上的适用性和优越性。
[0145]
以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。