一种针对弹性飞机的静气动弹性计算方法

1.本发明属于飞行器仿真设计领域，具体涉及一种针对弹性飞机的静气动弹性计算方法。


背景技术：

2.飞机实际在空中的运动时，会受到气流、速度、温度、空气压缩性等多种因素的影响，气动载荷加载在柔性机翼上会导致机翼发生结构变形，变形量较大时会对机翼气动特性产生负面影响。现代大型宽体客机机翼中复合材料的使用占比很高，机翼在飞行时会有很大的气动弹性变形，对气动性能产生较大的影响。气动弹性问题一直都是航空领域的一个研究热点。数值模拟分析是无破坏性的、可以个性化控制的、能够多次重复的、不受实际工作条件限制，可以实现的功能非常齐全的一种实验手段。利用数值模拟的结果，可以加深研究人员对实际模型的理解，快速找出研制过程中出现的问题的原因并提供解决方法。
3.气动弹性分析
4.实际情况中，飞行器的结构并不是绝对刚性的，飞行器外形结构受气动力作用会发生一定程度的弹性变形，这种结构的变形会反作用于气动力，引起气动力的改变，从而导致结构外形进一步的弹性变形，这样的结构变形与气动力交互作用的现象称为气动弹性现象。气动弹性效应是飞行器研究过程中不可忽视的重要部分。对弹性体飞行器的研究涉及到空气动力作用与弹性结构变形之间相互影响的问题，对飞行器的安全与性能起着关键的作用。随着航空航天领域的发展，气动弹性问题对飞行器的安全和发展的威胁逐渐突显，历史上就曾发生多起事故：1903年，lanley的单翼机首次作有动力的飞行试验时，就由于气动弹性效应而发生了机翼的断裂，并最终坠毁；1912年，英国的handly page轰炸机在作战时由于尾翼颤振而坠毁；20世纪30年代，英国的“蛾号”与“鸽号”飞机都因发生颤振而失事；40年代，德国的v
‑
2火箭曾遭遇颤振而导致结构破坏。弹性效应造成的严重损失使得人们逐步认识到结构设计环节考虑气动弹性效应的重要性。二十世纪中叶以来，研究者们将气动弹性力学定义成为一门独立的科学分支并不断发展，其研究的结果虽然使弹性问题造成的事故次数有所减少，但依然存在一些损失严重的事故：20世纪60年代，北京航空学院研制的无人靶机，因气动弹性造成机体失稳而坠毁；2001年，美国的高超声速验证机x
‑
43因控制舵面颤振而首飞失败，导致整个hyper
‑
x计划遭遇重创。由此可见，对飞行器弹性问题的研究已经成为飞行器研究的重要环节。现代飞行器的性能设计日益追求高速度、高机动性，结构设计致力于减重增效，而飞行速度不断提高的同时也带来了复杂的气动载荷，飞行器越来越呈现出轻结构、高弹性、高频响的控制系统特点，这些都会导致结构、空气动力和控制系统等方面的强烈非线性及其相互的强耦合作用，因而气动弹性与控制系统相耦合的问题在设计和飞行环节中广泛存在。由于通常情况下气动弹性现象会造成设计失效、结构破坏的有害影响，工程界常将其视为不利因素，这一矛盾突显了气动弹性力学与控制系统耦合研究的重要性和必要性。研究这类问题，涉及到结构动力学、非定常空气动力学和自动控制系统动力学等多学科领域的交叉，具有较强的综合性和复杂性。三者的关系可以用气动伺服弹
性力学三角形来表述，如图1所示。
5.目前，气动弹性研究的主要方法有两种：风洞实验和数值模拟。风洞实验在揭示现象、探索新课题方面准确可靠，因此，风洞实验在空气动力学的研究、各种飞行器的设计研制方面，以及其他流体有关的领域中，都有广泛应用，始终是气动弹性研究的主要分支。气动弹性实验大体上可以分为两大类：一类实验是用来为气动弹性分析取得原始数据，如飞行器结构的刚度试验、结构地面振动试验以及地面伺服弹性试验等；另一类实验用来获取数据分析气动弹性特性，如颤振模型风动试验、颤振飞行试验以及抖振试验等。然而需要指出的是，气动弹性问题交叉涉及众多学科，试验研究的开展面临较大的困难。例如静气动弹性实验中，测量模型的刚度会对气动特性产生一定的影响，通常的风洞实验采用的模型由于选材问题都具有较大的强度和刚度，而真实的飞行器其刚度比模型低得多。因此，风动实验中必需制造出一种适用的弹性模型，该模型能够准确模拟飞行器各部件弯曲和扭转刚度，用它进行风洞高动压模拟实验，用以测量模型刚度对气动特性的影响。首先，弹性模型的建立本身与实际飞行器相比很难保证弹性变形的模态完全一致；其次，当发生颤振导致模型结构破坏时，容易对风洞设备甚至实验人员造成伤害，具有相当大的危险性。风洞实验的基础原理是相似原理，这就要求风洞流场与真实飞行状态之间或能满足所有的相似准则，或能保证两个流场所对应的所有相似准则系数相等。通常的风洞实验很难完全满足上述两个条件，最常见的不满足相似准则的情况是亚跨声速风洞的雷诺数不符。以波音737为例，该飞机在巡航高度九千米以上，以每小时927公里的巡航速度飞行，雷诺数达re＝2.4
×
107，而在3米亚声速风洞实验中，风速每秒100米的情况下雷诺数仅约为re＝1.4
×
106，相差较大，实验结果则会受到影响。
6.与此同时，随着计算机技术和数值计算方法的发展，数值模拟方法的研究范围以及其结果的精确度均得到了突破性的提高，因此计算气动弹性成为气动弹性研究中重要的发展方向。schuster和liu等给出较为通用的计算气动弹性的定义，将采用数值分析手段、包含线性和非线性在内各种精度层次的气动弹性研究均列入了计算气动弹性的范畴。
7.依据研究的问题同结构、气动方面的非线性因素是否相关，计算气动弹性又可以分为经典线性气动弹性分析与比较复杂的非线性气动弹性分析。得益于空气动力学的快速发展，计算气动弹性得到了进一步的发展。
8.cfd方法采用了精确形式的流动控制方程，并且数值格式、离散方法、网格策略、并行计算技术等也逐渐成熟，目前，气动弹性计算方法正不断完善。
9.现代飞行器设计过程中可以用商业软件msc.nastran或自行编写的求解器进行求解，将气动弹性变形的影响引入到飞行器设计的方法和过程之中。
10.提高计算精度、扩展分析能力是气动弹性研究不懈追求的目标。因此，面对愈加复杂的飞行器外型、更加优越的飞行性能，研究包括非定常气动力、结构动力学和控制方程等相互耦合的多场耦合分析方法，是当前研究气动弹性问题的一项重要任务。
11.近年来，计算机技术和计算力学方法领域的快速发展使得采用计算流体力学进行气动弹性动力学仿真成为可能。研究气动弹性是研究固体形变在流场作用下的各种行为以及固体形变对流场影响这二者相互作用的一门学科。1946年，英国人collar用一个力的三角形对气动弹性问题作了形象的分类，如图2所示，三角形三个顶点分别代表空气动力、弹性力和惯性力，从而区分了各学科的研究范畴；三角形中心的动气动弹性力学需要对这三
种力进行耦合分析，是飞行力学、振动和静气弹等多学科领域的交叉，具有较强的综合性和复杂性
2.。
12.早期的气动弹性问题主要考虑的是机翼的颤振边界问题。第一状世界大战初期，英国的handley page轰炸机发生剧烈的尾翼颤振而坠毁，这一事故使得lanchester、bairstow和fage等人开始研究飞行器的颤振问题，直至1922年，他们研究发现，质量平衡可以有效地消除舵面颤振。1934年，theodorsen成功地得到了低速翼型在简谐振动情况下的非定常气动力精确解，这一理论被称为theodorsen理论，对气动弹性力学而言具有划时代的意义。
13.dugundji综合叙述了飞行器的气动弹性的研究进展，并且提出了研究气动弹性问题的四个主要手段：1)有效的数值和理论分析；2)风洞试验；3)地面振动结构测试；4)真实条件的飞行测试。
14.在经典的气动弹性问题中，早期计算气动力采用活塞、片条和准定常理论等比较简单的方法，文献
5.叙述了这一阶段国际上的重大研究成果。从二十世纪七十年代到九十年代，核函数法、小扰动位势理论和偶极子格网法开始应用于亚音速、跨音速和低超音速非定常气动力的分析中
6.，这些计算气动力的方法随后均有效应用在了气动弹性的分析上。到了二十世纪九十年代的中后期，随着计算机技术的快速发展，研究者们把euler方程和n
‑
s方程求解非定常气动力的技术运用到气动弹性分析方面，特别是跨音速和大攻角气动弹性分析方面，取得了显著效果，促使了气动弹性分析的飞速发展
[7][8]
。
[0015]
研究气动弹性问题，需要对非定常空气动力学和结构动力学(csd)等学科进行交叉研究，其中包括了cfd与csd之间的耦合；cfd计算与刚体运动涉及动边界的耦合；以及cfd计算与结构、运动三者之间的耦合等。其中，求解结构动力学系统主要有以下六种数值方法：1)振型叠加法；2)直接积分法；3)状态空间法；4)时间有限元法；5)一阶常微分方程组初值问题的数值解法；6)复模态法。其中直接积分法常用的有线性加速度法、newmark方法、wilson方法等。在研究直接模态叠加法过程中，邢誉峰等人利用dmsm策略，分析了等截面杆、梁的碰撞问题。文献
[9]
指出：这种方法可以用来获得结构弹性碰撞问题的解析解，而且这种方法不但可以用来分析平动结构的碰撞问题，还可以用来分析机构的各种弹性锁定问题；不但可以用来分析结构的点碰撞问题，还可以有效分析结构的线、面接触和碰撞等问题。关于cfd/csd的耦合方式，流体和结构系统进行独立求解，采用合适的交替算法完成两个计算场之间的耦合，降低了各时间步下积分的复杂度，同时也便于程序实行模块化。当前流固耦合模型主要分为紧耦合与松耦合，采用紧耦合能够减少耦合响应过程的时间延迟，时间精度得到了提高同时增大了时间步长，但计算量也大大增加；采用松耦合在每个物理时间步进行一次数据交换，计算量与正常的非定常流场分析相当。此外，farhat和zee等人：叶正寅和蒋跃文等人
[11]
还对二阶时间精度松耦合格式进行了研究。气动弹性数值模拟过程中，力与位移将通过插值技术在cfd和csd之间进行传递。因此存在两套网格：结构网格和气动网格。非定常气动力与结构位移等参数需要在结构/气动网格上进行交换，但是结构/气动网格两者的拓扑方式并不一致。因此必须要采用合适的插值方法完成数据的交换，插值方法需要满足以下四点要求：1)确保插值的光顺；2)能够精确地转换两套网格之间的信息；3)在网格较稀疏的情况下也能够完成插值；4)能够适用于复杂外形。目前比较常用的气动/结构网格间插值方法有常体积转换法(constant volume tetrahedron，cvt)、无限平板
样条法(infinite plate spline，ips)和薄平板样条法(thin plate spline，tps)等。


技术实现要素：

[0016]
本发明的目的在于提供一种针对弹性飞机的静气动弹性计算方法，以基于rbf方法能够通过每一个插值点的精确插值的特点，将气动结构交界面分成几个部分单独进行插值，减小插值矩阵维度，降低计算难度，提高效率。
[0017]
本发明的技术方案是：
[0018]
一种针对弹性飞机的静气动弹性计算方法，包括如下步骤：
[0019]
1)基于初始飞机翼身组合体刚体模型分别建立cfd计算模型和csd计算模型；
[0020]
2)进行cfd计算，求得流场气动数据，提取机翼表面压力数据，利用插值方法将气载荷转化成结构载荷加载到结构模型上；
[0021]
3)进行csd计算，求解加载了气动载荷的有限元方程，得到结构位移响应；
[0022]
4)利用插值方法把机翼的结构位移转化成气动网格的位移，得到表面气动网格的位移；
[0023]
5)对比收敛准则，机翼气动表面网格位移量是否小于给定的误差值，若不小于则转到步骤6；若小于，则结果收敛，输出计算结果；
[0024]
6)根据机翼表面气动网格位移，通过网格变形方法更新流场计算网格，转到步骤2进行迭代计算。
[0025]
对本发明上述步骤进一步限定：
[0026]
在步骤(1)中，以雷诺平均的n
‑
s方程进行流场求解，sst湍流模型通过有限体积法进行流场求解，时间推进方式采用隐式时间推进格式，分别采用roe格式进行通量计算和二阶迎风格式计算流动项。
[0027]
在步骤(2)中，所述rbf插值方法进行气动网格和结构网格之间的数据传递，反复迭代计算直至达到指定的收敛稳定条件。
[0028]
在步骤(3)中，在耦合界面上，所述气动网格的尺寸小于结构网格。
[0029]
在步骤(5)中，收敛准则的约束方程为
[0030]
进一步地，气动网格点位置的求解方程为
[0031][0032]
其中，
[0033]
本发明还提供了一种计算机存储介质，其上存储有计算机程序，该程序被处理器执行时实现上述方法的步骤。
[0034]
与现有技术的有益效果是
[0035]
把气动力求解方法、结构位移非线性求解方法和cfd/csd耦合方法三者结合，分别建立模型，满足仿真要求，建立统一的弹性飞机气动弹性仿真流程，计算弹性飞机的变形，
利用数值模拟的结果，可以加深研究人员对实际模型的理解，快速找出研制过程中出现的问题的原因并提供解决方法，减少设计投入，缩短设计周期。
附图说明
[0036]
图1为newton
‑
raphson迭代求解过程；
[0037]
图2为网格变形效果图；
[0038]
图3为静气动弹性分析流程；
[0039]
图4为crm翼身翼身组合体几何模型建模图；
[0040]
图5为crm模型表面网格图；
[0041]
图6为网格加密区域示意图；
[0042]
图7为crm模型机翼截面网格示意图；
[0043]
图8为机翼边界层网格细节图；
[0044]
图9为crm机翼csd计算网格图；
[0045]
图10为升力系数曲线结果与试验和参考文献对比例；
[0046]
图11为阻力系数曲线结果与试验和参考文献对比例。
具体实施方式
[0047]
下面结合实施例对本发明的具体实施方式进行描述，以便更好的理解本发明。
[0048]
实施例
[0049]
本实施例在计算步骤详尽阐述了方法步骤的推导过程，引用一些文献和现有技术，利于理解。
[0050]
本实施例提供基于飞机的静气动弹性的计算方法，包括：(一)气动力求解方法，(二)结构位移非线性求解方法，(三)对cfd/csd耦合方法；(四)将上述三个模型连成通路，建立静气动弹性分析流程
[0051]
(一)气动力求解方法
[0052]
随着cfd方法和计算机的发展，cfd计算在飞行器设计中被广泛应用，采用雷诺平均的n
‑
s方程进行流场求解。
[0053]
navier
‑
stokes方程
[0054]
三维守恒形式的可压缩n
‑
s方程如下：
[0055][0056]
式中，u是守恒变量。
[0057]
[0058][0059][0060][0061]
式中，ρ是气体密度，u，v，w是三个速度分量，p、e、t、κ分别为压力、总能、温度、热传导系数。p可以通过理想气体状态方程得出：
[0062][0063]
式中，γ是气体比热比，理想状态的空气取1.4。
[0064]
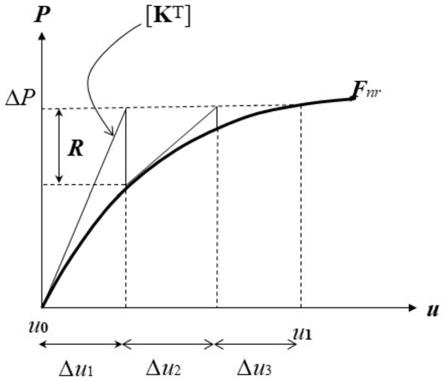
方程中粘性应力为：
[0065][0066][0067][0068][0069][0070]
[0071]
式中，μ是粘性系数。
[0072]
湍流模型
[0073]
标准k
‑
ω湍流模型
[13]
能够很好的模拟边界层的流动，在飞行器设计中被广泛使用。其方程为：
[0074][0075][0076]
式中：
[0077][0078]
湍流粘度低雷诺数修正系数α
*
为：
[0079][0080]
标准k
‑
ω湍流模型存在对来流条件非常敏感的问题，sstk
‑
ω(shear stress transport k
‑
ω)模型
[14]
是对k
‑
ω模型进行修正得到的。sstk
‑
ω模型同时具有k
‑
ω模型和k
‑
ε模型的稳定性与准确性，在近壁面使用k
‑
ω模型，在远场换成k
‑
ε模型，能够克服k
‑
ω模型对于来流条件敏感的缺陷，模型的稳定性得到了提高，sstk
‑
ω湍流模型在模拟有逆压梯度和激波存在的流场时更加准确和可靠。
[0081]
该模型的输运方程为：
[0082][0083][0084]
式中，k为湍动能，ω为湍动能的比耗散率，g
k
表示由平均速度梯度引起的湍流动能的生成项，g
ω
表示ω的生成项，γ
k
和γ
ω
分别是k和ω的有效扩散系数，y
k
和y
ω
分别是k和ω的湍流耗散，s
k
和s
ω
，为自定义的参数。
[0085]
[0086][0087]
该模型的混合函数为：
[0088]
f1＝tanh(φ
14
)
ꢀꢀ
(21)
[0089][0090][0091]
f2＝tanh(φ
24
)
ꢀꢀ
(24)
[0092][0093]
其中，y表示近壁面距离。混合函数f1在近壁面取值为1使用k
‑
ω湍流模型；在远场处取值为0，使用k
‑
ε湍流模型。
[0094]
langtry等人修正了湍流模型的混合函数，修正混合函数f1与f2类似。本发明采用sstk
‑
ω湍流模型通过有限体积法进行流场求解，时间推进方式采用隐式时间推进格式
[16]
，采用roe格式进行通量计算，采用二阶迎风格式计算流动项。
[0095]
(二)结构位移非线性求解方法
[0096]
当结构有较大的弯曲变形和扭转变形时，传统的线弹性分析方法无法描述结构的真实响应。为了得到精确的物理结果，必须考虑弹性变形对几何刚度的影响。结构在大变形时，会产生结构内力来平衡系统的外力。这种内力会增加结构的刚度，产生结构非线性。
[0097]
弹性力学基本方程
[0098]
平衡方程：
[0099]
σ
ij，j
+f
bi
＝0(i，j＝x，y，z)
ꢀꢀ
(26)
[0100]
式中，σ
ij
为应力张量，f为外载荷。
[0101]
几何方程：
[0102][0103]
式中，ε
ij
为应变张量，u为位移。
[0104]
本构方程：
[0105]
1)应变方程：
[0106][0107]
2)应力方程：
[0108][0109]
式中，e为弹性模量，ν为泊松比。
[0110]
通常采用变分原理对弹性平衡方程进行求解。根据虚位移和最小总势能原理，引入拉格朗日乘子，得到势能泛函π
h
：
[0111][0112]
式中，为应变能函数，v为物体体积，s为物体表面积，f为体力外载荷，t为面力外载荷。
[0113]
对π
h
进行变分，求出极值：
[0114][0115]
可以得到：
[0116][0117]
有限元方法
[0118]
对于简单的问题可以通过变分法求得精确的解析解，但对于复杂问题，求解解析解的难度非常大，因此在实际中一般都采用有限元方法
[18
‑
21]
进行数值计算。采用有限元方法进行结构求解时，先要将结构进行离散，计算单元刚度矩阵，然后装配总刚度矩阵，加载结构约束和外载荷后进行求解。
[0119]
有限元法得到的结果是一种近似解，结构网格越密，网格单元越小，越接近真实值，求解的精度会更高。因此，在实际应用时可以根据实际情况对一些应力和应变集中的地方进行网格加密以提高求解精度。在计算的时候，每个单元内部使用的是局部坐标系，在进行刚度矩阵装配时需要在全局坐标系下进行。
[0120]
单元的各个节点的位移{δ}
e
＝[u
i v
i w
i
]
t
可以进行装配得到全局位移{f}＝[u v w]
t
。
[0121]
{f}＝[n]{δ}
e
ꢀꢀ
(33)
[0122]
式中，[n]＝[in
i
]，n
i
为形函数，i是单位矩阵
[0123]
单元刚度矩阵可以通过求解弹性力学基本方程得到。每个单元的应变矩阵可以通过几何方程得到：
[0124]
{ε}＝[b]{δ}
e
ꢀꢀ
(34)
[0125]
对于六面体单元有：
[0126]
[b]＝[[b1] [b2]
ꢀ…ꢀ
[b8]]
ꢀꢀ
(35)
[0127][0128]
每个单元的应力矩阵为：
[0129]
{σ}＝[d]{ε}＝[d][b]{δ}
e
ꢀꢀ
(37)
[0130]
式中，[b]是单元几何矩阵，[d]是单元弹性矩阵，[s]＝[d][b]是单元应力矩阵。
[0131]
单元内节点力可以通过虚功原理求得：
[0132]
{f}
e
＝[k]{δ}
e
ꢀꢀ
(38)
[0133]
式中，[k]＝∫∫∫[b]
t
[d][b]dxdydz为单元内的刚度矩阵，
[0134]
内外力相互平衡：
[0135][0136]
将单元刚度矩阵进行装配得到总体刚度矩阵。总体结构平衡方程为：
[0137]
[k]{δ}＝{r}
ꢀꢀ
(40)
[0138]
式中，[k]是总体刚度矩阵，{δ}是结点位移，{r}施加在节点上的外部载荷。
[0139]
结构几何非线性分析方法
[0140]
迭代技术是求解几何非线性的有效方法，本发明中使用的是newton
‑
raphson方法，求解过程如图1所示：
[0141]
对于初始的结构模型，可以计算得到初始的刚度矩阵，然后施加一个外部载荷δp，求解方程(41)得到节点位移的增量：
[0142]
[k
t
(u0)]δu1＝δp
‑
f
nr
(u0)
ꢀꢀ
(41)
[0143]
式中f
nr
是结构内力，δu
i
是位移在载荷作用下的增量，是刚度矩阵。
[0144]
在静力学问题中，内外载荷是平衡的，newton
‑
raphson迭代计算收敛的度量是产生位移变形后的内力与外部载荷平衡：
[0145]
δp
‑
f
rr
＝0
ꢀꢀ
(42)
[0146]
如图1所示，由于在初始模型上使用了线性化假设，求解得到位移增量后更新的构型中内力与外部载荷有一个不平衡量r，不满足平衡状态。
[0147]
r＝δp
‑
f
nr
(u0+δu1)
ꢀꢀ
(43)
[0148]
下次计算根据初始刚度矩阵求得的位移增量更新几何构型，计算出新的刚度矩阵，得到新的位移增量：
[0149]
[k
t
(u0+δu1)]δu2＝δp
‑
f
rr
(u0+δu1)＝r
ꢀꢀ
(44)
[0150]
随着不断迭代，不平衡量r会越来越小，不断接近0，由于不平衡量r不会真正等于0，当r减小到一定程度，满足给定的残差值时，迭代收敛。得到结构位移u1：
[0151]
u1＝u0+(δu1+δu2+
…
+δu
i
)
ꢀꢀ
(45)
[0152]
newton
‑
raphson法能够在局部求解时快速收敛，要求初始值要接近真实值。实际上很难找到接近真实值的初始值。通常使用增量的方法
[23]
来解决这个问题。增量法是首先等分外部载荷p，每次加载δp求解收敛后，将结果作为下一增量步的初始值，直到所有载荷全部加载完成。将外部载荷等分j份时最后的节点位移u＝u0+u1+l+u
j
。
[0153]
(三)cfd/csd耦合方法
[0154]
气动弹性分析通过cfd/csd松耦合迭代求解，分别建立流场计算模型和结构计算模型利用商业软件独立进行计算。流场计算通过求解n
‑
s方程得到各项流动参数，结构响应计算通过有限元方法求得结构的位移响应。然后通过rbf插值方法进行气动网格和结构网格之间的数据传递，反复迭代计算直至达到指定的收敛稳定条件。
[0155]
气动载荷/结构位移传递方法
[0156]
采用cfd/csd松耦合方法进行计算，在迭代过程中，气动计算网格和结构计算网格是独立建模的，需要在气动网格和结构网格之间进行气动力和结构位移的传递。在耦合界面上气动网格的尺寸通常小于结构网格，在进行气动载荷传递时要满足能量守恒。径向基函数(rbf)方法可以满足能量守恒的要求，并且可以直接在离散点云之间传递数据，不依赖于网格。可以在结构网格和非结构网格上进行数据传递，rbf插值方法被广泛使用在气动弹性分析中。
[0157]
rbf方法通过散点生成的插值面能够通过每一个数据点，是一种精确的插值方法，利用这个特点可以将气动和结构的耦合面分成几个部分独立进行插值可以大大减小插值矩阵的维度，降低求解难度，提高效率。
[0158]
气动载荷和结构位移在耦合界面传递时要保持能量守恒，根据虚功原理有：
[0159][0160]
其中，δu
s
、δu
f
分别为耦合界面上结构网格点和气动网格点的虚位移，f
s
、f
f
分别为耦合界面上结构和气动网格的载荷。定义传递矩阵h，可以得到流场网格和结构网格在耦合面上网格点的气动和结构载荷以及结构和气动网格点的位移传递关系：
[0161]
u
f
＝hu
s
，f
s
＝h
t
f
f
ꢀꢀ
(47)
[0162]
本发明使用rbf方法进行气动结构耦合面的数据传递。径向基函数插值公式为：
[0163][0164]
式中：φ(||x||)为基函数，常见的基函数如表1所示，λp(x)
为低阶多项式，通常为λp(x)＝λ0+λ1x+λ2y+λ3z。不同的基函数适用于不同的问题，可以根据问题选取不同的基函数。
[0165]
表1 rbf基函数
[0166][0167][0168]
方程组有个n+4未知量，但是这里只有n个方程，是一个未定系统。
[0169]
要求解这个方程，增加一个约束方程：
[0170][0171]
假设流固耦合界面上有f
n
气动网格点，有s
n
个结构网格点。结构网格点结构变形后的位置u
sn
已知，带入rbf插值函数可以表示为下式：
[0172]
u
s
＝c
ss
a
ꢀꢀ
(50)
[0173]
式中
[0174]
u
s
＝[0 0 0 0 u
s
]
t
[0175][0176][0177]
[0178][0179]
可以解出未知量：
[0180][0181]
变形后的气动网格点位置可以通过如下矩阵解出：
[0182][0183][0184]
网格变形方法
[0185]
弹簧光顺方法假设相邻的网格点之间由一个弹簧进行连接，根据胡克定律有：
[0186][0187]
式中，是节点i、j的位移；n
i
是节点i的相邻节点数；k
ij
表示与两个节点i、j之间的弹簧刚度，定义如下：
[0188][0189]
式中，k
fac
是弹簧常数因子，取值在0和1之间，值越小，边界网格节点的位移对远处的网格节点的影响越大，能将变形传递的更远；值越大，边界网格节点的位移对远处的网格节点的影响越小，变形的网格集中在边界附近。
[0190]
网格点移动后，在弹簧的作用下会重新达到平衡状态，节点受到的弹力合力为0：
[0191][0192]
式中，m是迭代步数。计算完成后，新的网格节点坐标为：
[0193][0194]
扩散光顺方法
[24]
是一种隐式求解方法，消耗的计算资源要比弹簧光顺多，但变形后的网格质量要比弹簧光顺方法要好，相较于弹簧光顺，扩散光顺能够应用在网格大尺度变形上。网格节点的位移速度可以利用扩散方程求得，通过公式(60)更新网格节点坐标。
[0195]
扩散光顺方程如下：
[0196][0197]
式中，u是网格节点的运动速度，γ是扩散系数。
[0198][0199]
式中，d为网格节点与边界之间的距离，α为扩散系数，取值范围是[0，2]，值越大，
边界网格节点的位移对远处的网格节点的影响越大，能将变形传递的更远。
[0200]
新的网格节点位置：
[0201][0202]
式中，为新的网格节点位置，为旧的网格节点位置。
[0203]
具体地说，本实施例中使用扩散光顺来进行网格变形。
[0204]
图2为使用扩散光顺方法的二维翼型网格变形效果，翼型进行了3次旋转和平移，每次旋转25
°
，整个变形过程中机翼附近的网格质量(单元面积与最长边的比值除以等边三角形面积和边长的比值)一直高于0.4。
[0205]
(四)将上述三个模型连成通路，建立静气动弹性分析流程
[0206]
静气动弹性分析流程，如图3所示。
[0207]
1)基于初始飞机翼身组合体刚体模型分别建立cfd计算模型和csd计算模型；
[0208]
2)进行cfd计算，求得流场气动数据，提取机翼表面压力数据，利用插值方法将气载荷转化成结构载荷加载到结构模型上；
[0209]
3)进行csd计算，求解加载了气动载荷的有限元方程，得到结构位移响应；
[0210]
4)利用插值方法把机翼的结构位移转化成气动网格的位移，得到表面气动网格的位移；
[0211]
5)对比收敛准则，机翼气动表面网格位移量是否小于给定的误差值，若不小于则转到步骤6；若小于，则结果收敛，输出计算结果；
[0212]
6)根据机翼表面气动网格位移，通过网格变形方法更新流场计算网格，转到步骤2进行迭代计算。
[0213]
采用crm翼身组合体模型(如图4所示)来验证本实施例静气动弹性分析方法的准确性。crm构型是由nasa和dpw(drag prediction workshop)组织委员会其同研究出来的用于行业内进行cfd方法验证的构型
[25]
。设计巡航马赫数为0.85、设计升力系数为0.50。
[0214]
nasa对crm构型进行了2次风洞试验，分别在在langley实验室的ntf(national transonic facility)风洞
[26]
和ames 11
‑
ft跨音速风洞
[27]
。在ntf风洞进行的风洞试验中，试验模型缩比为0.027，表2.2为其基本几何参数：
[0215]
表2 crm模型几何参数
[0216][0217]
[0218]
本文基于ntf风洞试验模型生成cfd计算网格，网格是三棱柱和四面体的混合网格。模型表面为三角形网格，边界层采用三棱柱网格，空间网格采用四面体网格，机翼和尾流区进行了局部加密。为了研究网格收敛性，本文建立了三套cfd计算网格，分别为粗网格、中网格和细网格，网格量分别为591万、1053万和2103万，表2.3为2
°
迎角下网格收敛性计算结果。
[0219]
表3 crm流场网格收敛性研究
[0220][0221]
从表3可以看出，从中网格到细网格升力系数的变化小于0.001，中网格已经可以满足本研究计算精度的要求。为了降低计算成本，本实施例使用中网格来进行计算。
[0222]
以中网格为例介绍网格划分情况，
[0223]
图5为crm模型表面网格，图6为体网格加密区，图7为机翼展向截面网格，
[0224]
图8为机翼边界层网格。计算条件为ma＝0.85，re＝5
×
106。
[0225]
本实施例不考虑机身的变形影响，将csd计算模型简化为单机翼模型。风洞试验模型采用实心不锈钢材料，本实施例忽略模型的开孔将模型简化为实心模型。
[0226]
如图9所示，csd网格为四面体网格，网格数量为27万。csd计算模型弹性模量为73.1gpa，泊松比为0.33，边界条件为翼根固支。
[0227]
图10和图11为cfd计算结果和cfd/csd耦合计算结果与试验和王运涛等人[28]的结果进行的对比。从结果中可以看出，不考虑静气动弹性时，计算结果与试验结果误差很大，考虑静气动弹性的计算结果与试验结果的误差减小了很多。误差的来源主要是风洞试验使用了尾部支撑，存在着支撑干扰。王运涛等人在crm模型上加入尾部支撑后进行的静气动弹性计算结果基本与试验一致，说明他们的计算结果是可信的。本文的刚体计算结果和静气动弹性计算结果与王运涛等人的无尾部支撑的计算结果基本一致，可以说明本实施例的结果是可信的。
[0228]
以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。