一种基于神经网络模型的安全多方计算方法与流程

1.本发明涉及区块链技术领域，具体涉及一种基于神经网络模型的安全多方计算方法。


背景技术：

2.区块链是一个分布式的共享账本和数据库，具有去中心化、不可篡改、全程留痕、可以追溯、集体维护、公开透明等特点。这些特点保证了区块链的“诚实”与“透明”，为区块链创造信任奠定基础。基于区块链能够解决信息不对称问题，实现多个主体之间的协作信任与一致行动。区块链借助分布存储，虽然提高了数据的安全性并提供了信任基础，但同时也注定了数据在区块链上是公开透明的。随着区块链应用不断扩展延伸，涉及敏感隐私数据的行业在应用区块链时，就出现了无法保持数据隐私的问题。因此隐私计算的概念被提出，隐私计算（privacy computing）是指一种由两个或多个参与方联合计算约定函数的技术和系统。参与方在不泄露各自数据的前提下通过协作对他们的数据进行联合机器学习和联合分析。隐私计算的参与方既可以是同一机构的不同部门，也可以是不同的机构。其中，安全多方计算是隐私计算的一种实现技术。目前进行安全多方计算的技术有不经意传输、加密布尔电路和同态加密技术。其中不经意传输和加密布尔电路的方案能够进行任意目标函数的计算，但效率十分低下。同态加密目前仅能够进行加法的安全多方计算。导致安全多方计算技术难以推广使用，限制了区块链技术的发展。因而需要进一步研究执行效率更高的安全多方计算方案。
3.如中国专利cn111737011a，公开日2020年10月2日，公开了一种安全多方计算的实现方法，应用在安全多方计算参与方的代表节点上，其方法包括：确定本参与方符合安全多方计算协议的密态计算任务；将密态计算任务拆分为至少两个子任务，并将子任务分发给至少两个辅助节点进行计算；接收辅助节点返回的子任务的执行结果，根据子任务的执行结果生成符合安全多方计算协议的密态计算任务的计算结果。其基于同态加密进行安全多方计算，不能解决当前安全多方计算应用范围窄的技术问题。


技术实现要素：

4.本发明要解决的技术问题是：目前安全多方计算应用范围窄的技术问题。提出了一种基于神经网络模型的安全多方计算方法，借助神经网络模型拟合目标函数实现安全多方计算。
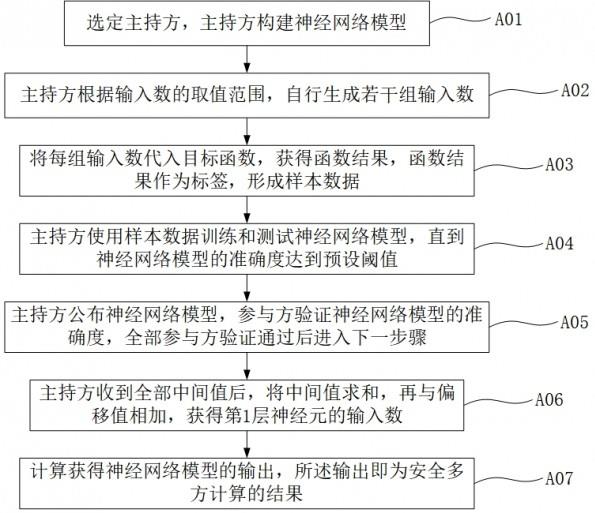
5.为解决上述技术问题，本发明所采取的技术方案为：一种基于神经网络模型的安全多方计算方法，包括：选定主持方，主持方构建神经网络模型；主持方根据输入数的取值范围，生成若干组输入数；将每组输入数代入目标函数，获得函数结果，函数结果作为标签，形成样本数据；主持方使用样本数据训练和测试神经网络模型，直到神经网络模型的准确度达到预设阈值；主持方公布神经网络模型，参与方验证神经网络模型的准确度，若验证通过则将验证结果签名，全部参与方验证通过后进入下一步骤；神经网络模型的第1层神经元
的输入数将是输入层神经元取值的加权和与偏移值的和，参与方将各自的隐私数代入加权和计算式，得到中间值，将中间值发送给主持方；主持方收到全部中间值后，将中间值求和，再与偏移值相加，获得第1层神经元的输入数；获得第1层全部神经元的输入数后，计算获得神经网络模型的输出，所述输出即为安全多方计算的结果。
6.作为优选，主持方训练神经网络模型达到预设阈值后，检查第1层每个神经元涉及的连接的权重值，若存在第1层的神经元仅涉及一条权重非零的连接，则丢弃该神经网络模型，重新构建神经网络模型并重新训练。
7.作为优选，参与方计算第1层神经元的中间值时，若中间值仅涉及参与方的一个输入数，则参与方执行以下步骤：从其他参与方中任选至少1个参与方，作为协同方，协同计算中间值；参与方将输入数拆分为若干个加数，加数数量为协同方数量加1；参与方保留一个加数，其余加数分别发送给协同方；参与方使用保留的加数计算中间值，将中间值发送给主持方；协同方计算对应中间值时，将自身输入数和获得的加数代入中间值的计算式，获得中间值，将中间值发送给主持方。
8.作为优选，主持方生成若干组输入数的方法，包括以下步骤：主持方向参与方索要每个输入数的取值范围；参与方将输入数的取值范围和分布概率反馈给主持方；支持方按照分布概率在输入数的取值范围内随机生成输入数。
9.作为优选，参与方将输入数的取值范围划分为若干个区间，计算每个区间的分布概率；将若干个区间的分布概率发送给支持方，支持方公开每个输入数的取值范围和分布概率；参与方验证准确度时，按照输入数的分布概率生成若干组输入数；将输入数代入目标函数获得函数结果；将输入数代入神经网络模型，获得神经网络模型的输出，与函数结果对比获得损失值；计算损失值占函数结果的百分比，获得平均损失百分比，若平均损失百分比低于预设阈值，则判定神经网络模型的准确度验证通过。
10.作为优选，主持方根据目标函数，选择划分量，所述划分量为目标函数中涉及指数函数的输入数，主持方根据划分量的取值范围，为划分量设置若干个区间，为每个区间建立一个神经网络模型，并将神经网络模型关联对应的区间，进行安全多方计算时，由划分量对应的参与方选择对应的神经网络模型并通知其他参与方。
11.作为优选，主持方构建神经网络模型时，执行以下步骤：设定阈值n，n为正整数；主持方分别计算目标函数对每个输入数的1阶偏导至n阶偏导；对于输入数，若目标函数的m阶偏导非常数，则主持方添加所述输入数的m次方作为神经网络模型的输入神经元。
12.本发明的实质性效果是：利用神经网络模型拟合任意目标函数，获得在一定允许误差范围内的安全多方计算方案，扩大了安全多方计算的应用范围，同时也提高了安全多方计算的效率；由于神经网络模型对目标函数的拟合存在一定的误差，因而消除了准确计算带来的数据泄露问题；采用协同计算使仅有一个输入数的参与方能够在保证隐私的前提下，参与到安全多方计算中。
附图说明
13.图1为实施例一安全多方计算方法流程示意图。
14.图2为实施例一协同计算方法示意图。
15.图3为实施例一生成输入数方法示意图。
16.图4为实施例一输入数分布概率示意图。
17.图5为实施例一准确度验证方法示意图。
18.图6为实施例一神经网络模型示意图。
19.图7为实施例二建立神经网络模型方法示意图。
20.其中：10、输入数，20、输入层，30、第1层，40、输出层。
具体实施方式
21.下面通过具体实施例，并结合附图，对本发明的具体实施方式作进一步具体说明。
22.实施例一：一种基于神经网络模型的安全多方计算方法，请参阅附图1，本方法包括以下步骤：步骤a01）选定主持方，主持方构建神经网络模型；步骤a02）主持方根据输入数的取值范围，生成若干组输入数；步骤a03）将每组输入数代入目标函数，获得函数结果，函数结果作为标签，形成样本数据；步骤a04）主持方使用样本数据训练和测试神经网络模型，直到神经网络模型的准确度达到预设阈值；步骤a05）主持方公布神经网络模型，参与方验证神经网络模型的准确度，若验证通过则将验证结果签名，全部参与方验证通过后进入下一步骤；步骤a06）神经网络模型的第1层神经元的输入数将是输入层神经元取值的加权和与偏移值的和，参与方将各自的隐私数代入加权和计算式，得到中间值，将中间值发送给主持方，主持方收到全部中间值后，将中间值求和，再与偏移值相加，获得第1层神经元的输入数；步骤a07）获得第1层全部神经元的输入数后，计算获得神经网络模型的输出，输出即为安全多方计算的结果。
23.主持方训练神经网络模型达到预设阈值后，检查第1层每个神经元涉及的连接的权重值，若存在第1层的神经元仅涉及一条权重非零的连接，则丢弃该神经网络模型，重新构建神经网络模型并重新训练。第1层的神经元仅涉及一条权重非零的连接，对应计算出的中间值，能够直接反推出输入数，会导致隐私泄露。出现这种情况的原因是神经网络模型的结构不合理或训练出现问题。应减小神经元的数量，或者降低权重接近0时的梯度。使权重被训练为0，属于神经网络训练中，经常会出现的异常情况。通常意味着梯度函数选择不合理。本方案仅对这种训练异常的情况做排除处理。
24.参与方计算第1层神经元的中间值时，若中间值仅涉及参与方的一个输入数，则参与方执行以下步骤，请参阅附图2，包括：步骤b01）从其他参与方中任选至少1个参与方，作为协同方，协同计算中间值；步骤b02）参与方将输入数拆分为若干个加数，加数数量为协同方数量加1；步骤b03）参与方保留一个加数，其余加数分别发送给协同方；步骤b04）参与方使用保留的加数计算中间值，将中间值发送给主持方；步骤b05）协同方计算对应中间值时，将自身输入数和获得的加数代入中间值的计算式，获得中间值，将中间值发送给主持方。请参阅附图6，如参与方甲拥有两个输入数：x1和x2，参与方乙拥有一个输入数：x3，主持方为
丙。神经网络模型通常包括一个输入层、一个输出层和若干个隐藏层，隐藏层也称为中间层，在一些简单的神经网络模型中，也可以没有隐藏层。输出层可以有一个神经元，也可以有多个神经元。较为典型的神经网络模型为全连接神经网络。即每层的神经元与上一层的神经元均连接。输入层也被称为第0层，相应的隐藏层被依次称为第1层、第2层等。图6中所示神经网络模型具有一个输入层20、一个输出层40和一个隐藏层，即第1层30。输入层10的神经元的输出即为输入数10，用于将输入数10导入神经网络模型。
25.其中，参与方乙因只有一个输入数而触发本步骤，参与方乙将输入数x3拆分为x3_1和x3_2，x3= x3_1+x3_2，将x3_1发送给参与方甲，保留x3_2。参与方甲计算的中间值temp1=a11*x1+a12*x2+a13*x3_1，参与方乙计算的中间值temp2=a13*x3_2，将temp1和temp2发送给主持方丙。主持方丙将temp1和temp2相加，获得结果即恰好为a11*x1+a12*x2+a13*x3。再加上偏移值b1，即获得第1层的一个神经元的输入值。将输入值代入激活函数即可获得该神经元的输出。虽然主持方丙能够计算出x3_2，但由于主持方丙无法从temp1中计算出x3_1，因而无法获得输入数x3的值。同时参与方甲虽然获知了x3_1的值，但参与方甲并不知晓temp2的值，因而也无法获得输入数x3的值，实现输入数x3的隐私保护。但应采取措施使参与方甲和主持方丙不进行合谋作恶。节点作恶不在本实施例讨论范围之内。本实施例假设节点均遵循步骤执行，不额外进行数据串通。但节点保持好奇心，即从获得的数据中，努力推算其他节点的输入数。
26.主持方生成若干组输入数的方法，请参阅附图3，包括以下步骤：步骤c01）主持方向参与方索要每个输入数的取值范围；步骤c02）参与方将输入数的取值范围和分布概率反馈给主持方；步骤c03）支持方按照分布概率在输入数的取值范围内随机生成输入数。请参阅附图4，为分布概率示意图。本实施例中采用的分布概率不是一个连续的函数，而是采用直方图的形式。具体而言，将输入数的取值范围划分若干个区间，计算输入数落入区间内的概率，作为该区间的分布概率。
27.请参阅附图5，主持方生成输入数以及参与方验证神经网络模型准确度的方法包括以下步骤：步骤d01）参与方将输入数的取值范围划分为若干个区间，计算每个区间的分布概率；步骤d02）将若干个区间的分布概率发送给支持方，支持方公开每个输入数的取值范围和分布概率；步骤d03）参与方验证准确度时，按照输入数的分布概率生成若干组输入数；步骤d04）将输入数代入目标函数获得函数结果；步骤d05）将输入数代入神经网络模型，获得神经网络模型的输出，与函数结果对比获得损失值；步骤d06）计算损失值占函数结果的百分比，获得平均损失百分比；步骤d07）若平均损失百分比低于预设阈值，则判定神经网络模型的准确度验证通过。
28.理论上，在已知目标函数的情况下，通过自主生成输入数，能够获得不限数量的带标签的样本。在不限定神经网络的层数、神经元数量以及神经网络的训练时间的情况下，神经网络是能够拟合出任意复杂的函数的。
29.进一步的，为了适当降低神经网络模型的训练时长，主持方根据目标函数，选择划分量，划分量为目标函数中涉及指数函数的输入数，主持方根据划分量的取值范围，为划分量设置若干个区间，为每个区间建立一个神经网络模型，并将神经网络模型关联对应的区间，进行安全多方计算时，由划分量对应的参与方选择对应的神经网络模型并通知其他参与方。
30.本实施例的有益技术效果是：利用神经网络模型拟合任意目标函数，获得在一定允许误差范围内的安全多方计算方案，扩大了安全多方计算的应用范围，同时也提高了安全多方计算的效率。由于神经网络模型对目标函数的拟合存在一定的误差，因而消除了准确计算带来的数据泄露问题。采用协同计算使仅有一个输入数的参与方能够在保证隐私的前提下，参与到安全多方计算中。
31.实施例二：一种基于神经网络模型的安全多方计算方法，同样的，本实施例为了在实施例一的基础上，进一步降低神经网络拟合的难度，节省神经网络训练的时间。主持方构建神经网络模型时，执行以下步骤，请参阅附图7，包括：步骤e01）设定阈值n，n为正整数；步骤e02）主持方分别计算目标函数对每个输入数的1阶偏导至n阶偏导；步骤e03）对于输入数，若目标函数的m阶偏导非常数，则主持方添加输入数的m次方作为神经网络模型的输入神经元。如目标函数为y=x1^2+3*x2，则目标函数对于x1的一阶偏导、二阶偏导非0，三阶偏导为0，对x2的一阶偏导非0，二阶偏导为0，则为x1建立1次方输入神经元和2次方输入神经元，对x2建立1次方输入神经元。将幂运算转换为加法运算，降低神经网络的复杂度。节省神经网络的训练时长。值得注意的是，即使不建立x1的2次方输入神经元，神经网络模型也能够通过大量样本数据的训练，获得拟合x1的平方的结果。其大致原理为，与x1输入神经元连接的多个隐藏层神经元分别具有不同的权重。当x1的取值与权重相当时，x1与权重的乘积即接近x1的2次方。当这样的隐藏层神经元足够多时，其计算精度将满足要求。同样的，对于x1的3次方，当权重与x1的平方相当时，权重与x1的乘积即接近x1的3次方。
32.同样的，对于指数函数、三角函数、对数函数等较为复杂的函数。当隐藏层神经元数量足够多时，使得输入数在其取值范围内，总存在某个隐藏层神经元连接的权重与输入数的乘积与对应函数值接近。其他不接近的神经元可以通过激活函数的抑制而不再传播。虽然会导致神经网络模型庞大复杂，但能够实施。
33.同时也意味着，实施例一记载的方案适合输入数的数量多，而目标函数涉及的计算较为简单的情况。而采用本实施例记载的技术方案时，由于增加了输入数的高次项，则能够计算更为复杂的目标函数。包括含高次项的加权和计算。实际上，对应能够进行泰勒展开的函数，实施例二都能够具有较高效率的进行拟合。如e^x、lnx的泰勒展开式中，包括x的1次方至n次方，当n足够大时，能够使误差低于阈值。从而本实施例大幅的扩大了神经网络模型能够高效率拟合的目标函数的范围。扩大了本方案高效率实施的范围。
34.以上所述的实施例只是本发明的一种较佳的方案，并非对本发明作任何形式上的限制，在不超出权利要求所记载的技术方案的前提下还有其它的变体及改型。