一种含高渗透率风电的配电网暂态电压量化评估方法

1.本发明涉及配电网暂态电压稳定性领域，具体涉及一种含高渗透率风电的配电网暂态电压量化评估方法。


背景技术：

2.近年来，风电在配电网中的渗透率逐步增加，这对电网的暂态电压稳定性提出了新的挑战。因此，建立一套科学、合理的评估理论来量化分析含高渗透率风电的配电网暂态电压稳定性的各影响因素变得尤为重要。
3.目前，已有部分文献提出了用于评估配电网暂态电压稳定性的指标，可总结为如下三类：
4.1)：以暂态响应恢复率和相对电压提升率这两个指标来衡量故障后母线电压的恢复速率和分布式电源对母线暂态电压的提升水平，进而表征母线暂态电压稳定性的强弱；
5.2)：利用系统平均均方根值变化频率指标，通过在监测期内统计各用户特定有效值变化测量事件的平均次数来反映配电网各节点电压暂降的情况；
6.3)：基于配单网中感应电动机负荷的t
‑
s特性，用故障极限切除时间来作为电网暂态电压稳定性的评估指标。
7.由于上述三类评估指标普遍缺乏工程理论与实践的统一标准，使其只适合于理论分析，难以大规模地应用到实际电网的暂态电压稳定性的评估场合。
8.在评估暂态电压稳定性这方面，相比配电网而言，国内外学者大都聚焦于输电网络，且针对不同特性的网络结构提出了不同类型的评估指标。针对直流受端电网，有文献提出用一组包含电压跌落的门槛值及其可接受的最大持续时间的二元表来描述系统中各节点暂态电压跌落是否安全的方法。在此基础上，部分文献结合现有的国家标准，通过构造单二元表来量化各节点电压跌落的程度，定义了多故障集下的节点电压暂降指标和系统电压暂降指标。
9.此外，为了能在不同电压阈值区间内有效量化节点电压暂降的程度，基于多二元表的暂态电压稳定裕度指标应运而生，为后续的暂态电压评估理论提供了新的思路。而对于直流送端电网，鉴于直流闭锁和换相失败等典型的故障形式，个别文献给出了基于多二元表的暂态压升严重性指标，旨在对呈现暂态过电压特性的母线电压进行快速评估。
10.以上用于输电网的评估指标大都局限于具体的网络背景，且仅能对呈现单一暂态特性下的母线电压进行评估，对于扰动后具有多种暂态特性的母线电压，其无能为力。此外，针对任意的故障形式和特定的扰动类型，现有的评估指标普遍存在无法兼顾的问题，使得它们应用场景严重受限。
11.为此，基于具体工程实践，亟需提出一种适用性强，应用范围广的暂态电压安全裕度指标、能对影响配电网暂态电压稳定性的各影响因素有效评估的方法。


技术实现要素：

12.针对现有的用于评估电网暂态电压稳定性的裕度指标存在的问题，本发明提供一种含高渗透率风电的配电网暂态电压量化评估方法，能更全面、更广范围地衡量暂态电压的变化程度；该量化评估方法不受扰动形式和运行工况的限制，可准确反映实测母线的响应情况
13.本发明采取的技术方案为：
14.一种含高渗透率风电的配电网暂态电压量化评估方法，首先针对电压暂降的场景，构建电压暂降安全裕度指标；接着，构建出适用于电压暂升情形下的电压暂升安全裕度指标；通过引入阶跃因子，构造基于改进多二元表的暂态电压安全裕度指标，并结合风电出力特性对该指标做出相应的修正；再次，定义区域电压合格率指标、区域电压安全裕度指标以及区域电压失稳风险指标；最后，利用所提指标对含高渗透率风电的配电网中影响暂态电压稳定性的各影响因素进行评估。
15.一种含高渗透率风电的配电网暂态电压量化评估方法，包括以下步骤：
16.步骤1：针对电压暂降的场景，基于二元表判据，提出用于量化评估母线电压稳定裕度的电压暂降安全裕度指标；
17.步骤2：针对电压暂升的场景，构建电压暂升安全裕度指标，通过引入阶跃因子，构造基于改进多二元表的暂态电压安全裕度指标，并考虑风电出力的间歇性和不可控性客观因素对指标评估结果造成的影响，进而对基于改进多二元表的暂态电压安全裕度指标做出相应的修正；
18.步骤3：定义区域电压合格率指标、区域电压安全裕度指标、区域电压失稳风险指标；
19.步骤4：对含高渗透率风电的配电网系统进行仿真分析，利用区域电压合格率指标、区域电压安全裕度指标、区域电压失稳风险指标，对该配电网中影响暂态电压稳定性的各影响因素进行评估。
20.所述步骤1中，电压暂降是指电力系统中某点工频电压的方均根值突然降至 0.1p.u.～0.9p.u.，并在短暂持续10ms～1min后恢复正常的现象。电压暂降的发生不仅会使生产线上电机停机、变频器失压保护动作、可编程逻辑控制器(plc)失灵，还会给用户带来巨大的经济损失。
21.所述步骤1中，二元表判据是数学上用来表征状态量x偏移过程的可接受性的一种评判准则。对于任意动力系统描述的动态过程，二元表判据(x
cr
，t
cr
)规定，若状态量x超过预设值x
cr
的最长持续时间t
b
不超过t
cr
时，该状态量的偏移是可以接受的。因此，电力系统中通过设置电压二元表(v
cr
，t
cr
)来要求某母线电压v
i
低于预设门槛值v
cr
的最长持续时间t
b
不超过规定时间t
cr
，当某母线暂态电压满足此条件时，则认为该母线的暂态电压稳定，否则暂态电压失稳。
22.所述步骤1中，电压暂降安全裕度指标是对传统的基于多二元表的暂态电压稳定裕度指标的量化方法进行改进后的一套用于评估在电压跌落的暂态过程后，各母线电压稳定裕度大小的度量标准，具体如公式(1)所示：
[0023][0024]
式(1)中，η
i.d.n
为n个低电压多二元表约束下的母线i的电压暂降指标；n为所设低电压二元表的个数；v
cr.d.n
为第n个低电压二元表的电压阈值；v
cr.d.k
为第k个低电压二元表的电压阈值；t
i.d.n
为故障清除后的恢复过程中，母线i的电压高于第n个低电压二元表电压阈值的初始时刻；t
i.d.0
为故障清除时刻；t
i.d.k
为故障清除后的恢复过程中，母线i的电压高于第 k个低电压二元表电压阈值的初始时刻；t
i.d.k
‑1为故障清除后的恢复过程中，母线i的电压高于第k
‑
1个低电压二元表电压阈值的初始时刻；k
d.n
为第n个电压阈值与第n
‑
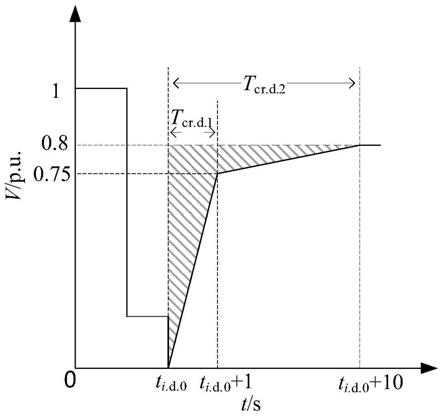
1个电压阈值之间区域的权重系数；k
d.k+1
为第k+1个电压阈值与第k个电压阈值之间区域的权重系数； k
d.k
为第k个电压阈值与第k
‑
1个电压阈值之间区域的权重系数；v
i
(t)为母线i的电压响应曲线；∑表示求和符号；z表示整数。
[0025]
其中，权重系数k
d.1
、k
d.2
、k
d.3
，
……
，k
d.n
求解过程如公式(2)所示：
[0026][0027]
式(2)中，t
cr.d.n
为故障清除后母线电压低于v
cr.d.n
的最大允许时长，即第n个低电压二元表的时间阈值。
[0028]
所述步骤2中，电压暂升是指电力系统因突然甩负荷、大容量电容器组接入等大扰动作用导致的某点工频电压的方均根值暂时上升至1.1p.u.～1.8p.u.，并在短时持续10ms～1min 后恢复正常的现象。过长持续时间的电压暂升会严重威胁各电力设备的使用寿命。
[0029]
所述步骤2中，电压暂升安全裕度指标是一套基于改进多二元表判据的用于评估在呈现短时过电压特性的暂态过程中，各母线电压稳定裕度大小的度量标准，具体如公式(3) 所示：
[0030][0031]
式(3)中，η
i.r.m
为m个过电压多二元表约束下母线i的电压暂升指标；m为所设过电压二元表的个数；v
i
(t)为母线i的电压响应曲线；v
cr.r.k+1
为第k+1个过电压二元表的电压阈值； t
i.r.k
为母线i电压在扰动后的上升过程中初次高于第k个过电压二元表电压阈值的时
刻； t
i.r.k+1
为母线i电压在扰动后的上升过程中初次高于第k+1个过电压二元表电压阈值的时刻； t
i.r.m
为母线i电压在扰动后的上升过程中初次高于第m个过电压二元表电压阈值的时刻； t'
i.r.k
为母线i电压在上升结束后的下降过程中初次等于第k个过电压二元表电压阈值的时刻；t'
i.r.k+1
为母线i电压在上升结束后的下降过程中初次等于第k+1个过电压二元表电压阈值的时刻；t'
i.r.m
为母线i电压在上升结束后的下降过程中初次等于第m个过电压二元表电压阈值的时刻；k
r.k
为{0≤v
i
(t)≤v
cr.r.k+1
}∩{t
i.r.k
≤t≤t
i.r.k+1
}之间区域的权重系数，∩表示交集； k
r.m
为{0≤v
i
(t)≤v
cr.r.m+1
}∩{t
i.r.m
≤t≤t'
i.r.m
}之间区域的权重系数。
[0032]
其中，权重系数k
r.m
由公式(4)解得，
[0033][0034]
式(4)中，t
cr.r.m
为在扰动后的电压恢复过程中电压大于阈值v
cr.r.m
的最大允许时长，即第 m个过电压二元表的时间阈值；v
cr.r.m
为第m个过电压二元表的电压阈值。
[0035]
所述步骤2中，阶跃因子的引入是为将电压暂降安全裕度指标与电压暂升安全裕度指标有效结合，它是与传统阶跃函数ε(t)具有相似函数特性的函数，但其具有更好的光滑性，是个光滑函数，具体如公式(5)所示：
[0036][0037]
式(5)中，e为自然常数；t为时间；ω为峰度参数，用来表征函数的陡峭程度。
[0038]
阶跃因子σ(t)具有如下特性：
[0039]
a)t<0时，σ(t)＝0；
[0040]
b)t≥0时，σ(t)＝1；
[0041]
c)
[0042]
所述步骤2中，基于改进多二元表的暂态电压安全裕度指标是综合了电压暂降安全裕度指标和电压暂升安全裕度指标后的适用于在电压暂降、电压暂升复合场景下，评估各母线电压稳定裕度大小的一套度量标准，具体如公式(6)所示：
[0043][0044]
式(6)中，η
i.n.m
为n个低电压多二元表和m个过电压二元表约束下的母线i的暂态电压安全裕度指标；η
i.d.n
为n个低电压多二元表约束下的母线i的电压暂降指标；η
i.r.m
为m个过电压多二元表约束下的母线i的电压暂升指标。
[0045]
所述步骤3中，区域电压合格率指标，是综合了电网中所有母线处可能发生的各类故障后，针对某研究区域或系统定义的该区域或系统下电压合格母线占该区域所有母线的
百分比，具体如公式(7)所示：
[0046][0047]
式(7)中，p
a
为考虑m个典型故障集及整个系统所有n个负荷母线后的区域a电压合格率指标；n
a.b.j
为负荷母线b处发生故障j时，区域a内电压合格母线的数量，当母线i的η
i.n.m
＜1时，即可认为母线i为电压合格母线；n
a
为区域a内的所有的负荷母线的数目；δ
j
为故障j的权重系数，数值上等于其发生的概率，由于各典型故障相互独立，故有
[0048]
所述步骤3中，区域电压安全裕度指标，是综合了电网中所有母线处可能发生的各类故障后，针对某研究区域或系统定义的该区域或系统下所有电压合格母线的平均暂态电压安全裕度指标，具体如公式(8)所示：
[0049][0050]
式(8)中，η
a
为区域电压安全裕度指标；η
i.n.m.b.j
为负荷母线b处发生故障j时，区域a内电压合格母线i在考虑了n个低电压多二元表和m个过电压二元表后的暂态电压安全裕度指标。
[0051]
所述步骤3中，区域电压失稳风险指标，是考虑到在某些特定故障的作用下，区域的母线电压可能全部失稳情形后，定义的该区域下所有暂态电压失稳母线的平均安全裕度指标，具体如公式(9)所示：
[0052][0053]
式(9)中，η'
a
为区域电压失稳风险指标；η'
i.n.m
为考虑了n个低电压多二元表和m个过电压二元表后的该区域中暂态电压失稳母线i的安全裕度指标。
[0054]
所述步骤4中，量化的含高渗透率风电的配电网中，影响暂态电压稳定性的各影响因素具体包括：
[0055]
①
：双馈风机的接入方式；
[0056]
②
：电动机负荷的分布情况、接入位置；
[0057]
③
：负荷功率突增扰动；
[0058]
④
：负荷功率突减扰动。
[0059]
所述步骤4中，暂态电压稳定性是指电力系统在发生大的扰动后各负荷节点不发生电压崩溃，能维持节点电压为可接受值的能力。
[0060]
本发明一种含高渗透率风电的配电网暂态电压量化评估方法，技术效果如下：
[0061]
1)在低电压多二元表数目相同的前提下，本发明所构造的电压暂降安全裕度指标评估裕度更大，能更全面、更广范围地衡量暂态电压的变化程度；
[0062]
2)由于引入的阶跃因子，暂态电压安全裕度指标能同时应用于电压暂降和电压暂升的评估场合，并能在评估过程中有效避免因指标安全域重叠而导致的误判问题；
[0063]
3)将新能源出力的间歇性和不可控性等客观因素考虑在内，合理修正了暂态电压安全裕度指标，提高了该指标在多变环境场景下的适用性。
[0064]
4)仿真结果证实，本发明的量化评估指标不受扰动形式和运行工况的限制，可准确反映实测母线的响应情况。
[0065]
利用所提指标对含高渗透率风电的配电网进行量化评估，验证了该指标的有效性和普适性，并得如下结论：
[0066]
(1)、双馈风机采取分散接入方式有利于改善系统的暂态电压稳定性，且更适用于高渗透的背景；
[0067]
(2)、当配电网含有感应电动机负荷时，在面临相同的故障下，电动机负荷距风机的电气距离越近，系统的暂态电压稳定性越好；
[0068]
(3)、针对大容量电动机接入的情形，电动机接入位置距离风机越远，系统的暂态电压稳定性越好；
[0069]
(4)、对于负荷功率的突变，无论是负荷的突增还是负荷的突减，风电渗透越大系统承受负荷扰动的能力就越强，系统暂态电压稳定性越好，且功率突变负荷距风机越近，负荷扰动对系统暂态电压稳定性的影响就越小。
附图说明
[0070]
图1为电压暂降示意图。
[0071]
图2为修正后的母线电压临界跌落面积示意图。
[0072]
图3为传统的基于多二元表的暂态电压稳定裕度指标的约束区域示意图。
[0073]
图4为电压暂升示意图。
[0074]
图5为含多波动过程的电压响应曲线示意图。
[0075]
图6为含多波动过程的电压暂降响应曲线示意图。
[0076]
图7为含多波动过程的等效电压暂降响应曲线示意图。
[0077]
图8为ieee15节点配电网系统示意图。
[0078]
图9为不同工况下关键母线的电压波形图。
[0079]
图10(a)为工况1下关键母线的暂态电压波形图；
[0080]
图10(b)为工况2下关键母线的暂态电压波形图。
[0081]
图11为预设工况下关键母线的暂态电压波形图。
[0082]
图12为相同容量电动机接入不同位置时关键母线的暂态电压波形图。
[0083]
图13为功率突增时关键母线的暂态电压波形图。
[0084]
图14为不同负荷突增时关键母线的暂态电压波形图。
[0085]
图15为功率突减时关键母线的暂态电压波形图。
[0086]
图16为不同负荷突减时关键母线的暂态电压波形图。
具体实施方式
[0087]
一种含高渗透率风电的配电网暂态电压量化评估方法，包括以下步骤：
[0088]
步骤1：针对电压暂降的场景，基于二元表判据，提出用于量化评估母线电压稳定裕度的电压暂降安全裕度指标；
[0089]
步骤2：针对电压暂升的场景，构建电压暂升安全裕度指标，通过引入阶跃因子，构造基于改进多二元表的暂态电压安全裕度指标，并考虑风电出力的间歇性和不可控性等客
观因素对指标评估结果造成的影响，进而对该指标做出相应的修正；
[0090]
步骤3：在此基础上，定义区域电压合格率指标、区域电压安全裕度指标以及区域电压失稳风险指标；
[0091]
步骤4：对含高渗透率风电的配电网系统进行仿真分析，利用所提指标，对该配电网中影响暂态电压稳定性的各影响因素进行评估。
[0092]
下面结合附图，对优选实例进行详细说明:
[0093]
1、评估之前需预先设置好作为评估依据的n个低电压多二元表和m个过电压多二元表，针对图1所示的电压暂降场景，用电压暂降稳定裕度指标量化出实测母线电压的稳定裕度，如公式(1)所示：
[0094][0095]
式(1)中，η
i.d.n
为n个低电压多二元表约束下的母线i的电压暂降指标；n为所设低电压二元表的个数；v
cr.d.n
为第n个低电压二元表的电压阈值；v
cr.d.k
为第k个低电压二元表的电压阈值；t
i.d.n
为故障清除后的恢复过程中，母线i的电压高于第n个低电压二元表电压阈值的初始时刻；t
i.d.0
为故障清除时刻；t
i.d.k
为故障清除后的恢复过程中，母线i的电压高于第k 个低电压二元表电压阈值的初始时刻；t
i.d.k
‑1为故障清除后的恢复过程中，母线i的电压高于第k
‑
1个低电压二元表电压阈值的初始时刻；k
d.n
为第n个电压阈值与第n
‑
1个电压阈值之间区域的权重系数；k
d.k+1
为第k+1个电压阈值与第k个电压阈值之间区域的权重系数； k
d.k
为第k个电压阈值与第k
‑
1个电压阈值之间区域的权重系数；v
i
(t)为母线i的电压响应曲线；∑表示求和符号；z表示整数。
[0096]
其中的权重系数k
d.1
、k
d.2
、k
d.3
，
……
，k
d.n
可由图2所示的修正后的电压临界跌落面积逐级求解而得，求解过程如公式(2)所示：
[0097][0098]
式(2)中，t
cr.d.n
为故障清除后母线电压低于v
cr.d.n
的最大允许时长，即第n个低电压多二元表的时间阈值。
[0099]
与传统的基于多二元表的暂态电压稳定裕度指标相比，本发明构造的电压暂降安全裕度指标在量化电压暂降稳定裕度这方面具有一定的优势，现作如下说明。
[0100]
基于多二元表的电压稳定裕度指标是在第n个低电压二元表所规定的允许时长内构造约束区域。以低电压多二元表(0.80p.u.,10s)、(0.75p.u.,1s)为例，将其约束区域进
行还原，如图3中阴影部分所示。此时的约束区域面积为s
总
＝2s1+s2＝2
×
(1
‑
0.8)+1
×
(0.8
‑
0.75)＝0.45，
[0101]
在相同的低电压多二元表作用下，利用发明方法构造出的约束区域面积 s'
总
＝0.5
×
0.75
×
1+0.5
×
(0.8
‑
0.75)
×
(10+1)＝0.65，可见s'
总
＞s
总
，且随着低电压二元表个数n增加，总有s'
总
＞s
总
，
△
s＝s'
总
‑
s
总
呈现递增的趋势。这表明在考虑相同数目的低电压多二元表约束时，本发明构造的约束区域大于传统多二元表暂态电压的约束区域。约束区域越大，则代表该指标的评估裕度越大，能更全面、更大范围地衡量母线暂态电压的变化程度。此外，当低电压二元表个数为n时，传统的多二元表稳定裕度指标的评估范围总落在t∈[t
i.d.0
, t
i.d.0
+t
cr.d.n
]区间内，若在该区间下评估出母线i暂态电压失稳，并不能判定在整个电压恢复过程中母线i暂态电压是失稳的，其原因是没有充分考虑母线i暂态电压在t
cr
.d.n
‑
1，...，t
cr.d.2
、 t
cr.d.1
这剩余的n
‑
1个时间阈值内是否失稳，而本发明所提的方法正好弥补了这一点。
[0102]
2、针对如图4所示的扰动发生后母线电压出现暂升的情形，量化出该母线的电压暂升安全裕度指标，如公式(3)所示：
[0103][0104]
式(3)中，η
i.r.m
为m个过电压多二元表约束下母线i的电压暂升指标；m为所设过电压二元表的个数；v
i
(t)为母线i的电压响应曲线；v
cr.r.k+1
为第k+1个过电压二元表的电压阈值；t
i.r.k
为母线i电压在扰动后的上升过程中初次高于第k个过电压二元表电压阈值的时刻；t
i.r.k+1
为母线i电压在扰动后的上升过程中初次高于第k+1个过电压二元表电压阈值的时刻；t
i.r.m
为母线i电压在扰动后的上升过程中初次高于第m个过电压二元表电压阈值的时刻；t'
i.r.k
为母线i电压在上升结束后的下降过程中初次等于第k个过电压二元表电压阈值的时刻； t'
i.r.k+1
为母线i电压在上升结束后的下降过程中初次等于第k+1个过电压二元表电压阈值的时刻；t'
i.r.m
为母线i电压在上升结束后的下降过程中初次等于第m个过电压二元表电压阈值的时刻；k
r.k
为{0≤v
i
(t)≤v
cr.r.k+1
}∩{t
i.r.k
≤t≤t
i.r.k+1
}之间区域的权重系数，∩表示交集；k
r.m
为 {0≤v
i
(t)≤v
cr.r.m+1
}∩{t
i.r.m
≤t≤t'
i.r.m
}之间区域的权重系数。
[0105]
其中的权重系数k
r.m
可由公式(4)解得。
[0106][0107]
式(4)中，t
cr.r.m
为在扰动后的电压恢复过程中电压大于阈值v
cr.r.m
的最大允许时长，即第m 个过电压多二元表的时间阈值；v
cr.r.m
为第m个过电压二元表的电压阈值。
[0108]
3、引入阶跃因子σ(t)，如公式(5)所示：
[0109]
[0110]
式(5)中，e为自然常数；t为时间；ω为峰度参数，用来表征函数的陡峭程度。
[0111]
4、将电压暂降安全裕度指标与电压暂升安全裕度指标通过阶跃因子σ(t)有效结合，得到实测母线基于改进多二元表的暂态电压安全裕度指标，如公式(6)所示：
[0112][0113]
式(6)中，η
i.n.m
为n个低电压多二元表和m个过电压二元表约束下的母线i的暂态电压安全裕度指标；η
i.d.n
为n个低电压多二元表约束下的母线i的电压暂降指标；η
i.r.m
为m个过电压多二元表约束下的母线i的电压暂升指标。
[0114]
若母线电压在扰动结束后的恢复过程当中伴随多个波动或振荡的过程，如图5所示，此时对原有的母线暂态电压安全裕度指标做出修正。修正思路如下：
[0115]
针对电压暂降指标，在整个仿真时长内综合所有的波动或振荡的时段，规定母线电压响应曲线在相邻电压阈值之间区域下的跌落面积为该区间内相邻电压阈值与母线电压响应曲线所包围的所有曲边梯形面积之和。而对于电压暂升指标，规定母线电压响应曲线在高于某一电压阈值下的上升面积为该电压阈值与相邻的下级电压阈值与母线电压响应曲线所包围的所有曲边梯形面积之和以及在曲线经过该电压阈值的所有时间段内该过电压阈值与时间轴所包围的面积之和。该修正方法的科学性在于对于任意的电压响应波形总可借助平移变换，将其转化成形状不同但冲量相等的等效电压波形，同一系统在相同时间段内被这两种暂态电压波形作用时，对外输出的能量是相同的，正如图6、图7示例所示。
[0116]
5、计算区域电压合格率指标来确定研究区域内电压合格母线的比重，如公式(7)所示：
[0117][0118]
式(7)中，p
a
为考虑m个典型故障集及整个系统所有n个负荷母线后的区域a电压合格率指标；n
a.b.j
为负荷母线b处发生故障j时，区域a内电压合格母线的数量，当母线i的η
i.n.m
＜1 时，即可认为母线i为电压合格母线；n
a
为区域a内的所有的负荷母线的数目；δ
j
为故障j 的权重系数，数值上等于其发生的概率，由于各典型故障相互独立，故有
[0119]
6、计算区域电压安全裕度指标来表征研究区域的暂态电压稳定裕度，如公式(8)所示：
[0120][0121]
式(8)中，η
a
为区域电压安全裕度指标；η
i.n.m.b.j
为负荷母线b处发生故障j时，区域a内电压合格母线i在考虑了n个低电压多二元表和m个过电压二元表后的暂态电压安全裕度指标。
[0122]
7、计算区域电压失稳风险指标来反映研究区域的暂态电压失稳程度，如公式(9)所示：
[0123][0124]
式(9)中，η'
a
为区域电压失稳风险指标；η'
i.n.m
为考虑了n个低电压多二元表和m个过电压二元表后的该区域中暂态电压失稳母线i的安全裕度指标。
[0125]
下面将通过实施例进一步说明本发明技术效果：
[0126]
搭建典型配电网系统并进行时域仿真分析，如图8所示，利用所提指标对该系统评估，在量化影响配电网暂态电压稳定性的若干影响因素的同时，验证该指标的有效性和普适性。仿真时预设的风机低电压多二元表和过电压二元表如下：[0.80p.u.,10s]、[0.75p.u.,1s]、 [0.7p.u.,0.2s]、[0.65p.u.,0.1s]、[1.1p.u.,1.2s]、[1.15p.u.,0.1s]，评估时以暂态电压问题最严重的关键母线为监测对象，与区域暂态电压合格率指标、暂态电压安全裕度指标、暂态电压失稳风险指标一同来表征统的暂态电压稳定性。此外，由于该系统母线数目不多，分析时将整个系统看成了一个区域。
[0127]
1)双馈风机的接入方式：
[0128]
为了研究双馈风机接入方式对暂态电压稳定性的影响情况，现按照如下工况依次将双馈风机接入系统进行仿真分析。工况一：1台风机经母线8接入电网；工况二：2台风机分别经母线7、母线8接入电网；工况三：4台风机分别经母线5、母线7、母线8、母线 15接入电网；工况四：6台风机分别经母线5、母线7、母线8、母线12、母线13、母线 15接入电网。三种工况下风电的总渗透率均为80％，且各工况下每台风机出力均相等。0.1s 时，依次在母线3处设置ab两相接地短路故障、abc三相短路故障，5个周波后故障被清除，此时对应的m＝2，δ1＝0.8，δ2＝0.2。经仿真计算得到两种典型故障下的该区域暂态电压合格率指标、暂态电压安全裕度指标、暂态电压失稳风险指标，如表1所示。
[0129]
表1风机不同接入方式下的区域暂态电压稳定性指标
[0130][0131]
图9给出了三相短路故障后4种工况下筛选出的关键母线集中暂态电压问题最严重的母线电压波形图。对比可见，表1的计算结果能真实反映图9所示的仿真波形的变化趋势。
[0132]
表2分别以工况一和工况四为例，给出了不同风电渗透率下区域暂态电压安全裕度指标、暂态电压失稳风险指标的变化趋势，两种工况中的关键母线暂态电压波形分别如图10 (a)、图10(b)所示。
[0133]
表2典型工况下风电渗透率与区域暂态电压稳定性指标的关系
[0134][0135][0136]
分析表2中的计算结果可知，在同一位置相同故障集的作用下，集中接入方式的区域暂态电压安全裕度指标随着风电渗透率的增加而增加，此时区域暂态电压失稳风险在递增。而分散接入方式的区域暂态电压安全裕度指标随着风电渗透率的增加而基本不变。可见在高渗透率的背景下，风机以分散接入的接入方式更有利于系统的暂态电压稳定性。
[0137]
如图10(a)、图10(b)中，风电渗透率越高，故障后对母线电压的抬升效果就越显著，也体现此时母线的电压暂升安全裕度指标愈大，区域暂态电压失稳风险愈高，对应了表3中的结果。
[0138]
2)电动机负荷的分布情况、接入位置：
[0139]
根据电气距离的远近，参照表3预设的工况，将原系统的部分负荷替换为感应电动机，在保证电动机负荷占比不变的前提下将双馈风机通过母线8接入电网，0.1s时由两相接地短路故障和三相短路故障构成的典型故障集作用于母线3处，0.2s后清除故障。得表4所示的仿真结果和图11所示的关键母线的暂态电压波形图。
[0140]
表3感应电动机在系统的分布情况
[0141][0142]
表4预设工况下的区域暂态电压稳定性指标
[0143][0144]
表4和图11均说明，在相同的风电渗透率下，感应电动机群距双馈风机的电气距离越近，故障后区域暂态电压稳定性越好，相应的暂态电压失稳风险越低。可见双馈风机与电动机负荷的相对位置将会影响系统的暂态电压稳定性。
[0145]
在相同风电渗透率下，同一容量的异步电动机在不同位置接入对系统暂态电压稳定性的影响不尽相同。现以单机聚合的方式将100台单机容量为4kw鼠笼式异步电动机等值
成 1台装机容量400kw的电动机，并于0.1s时依次于母线2、母线3、母线4处接入配电网，配电网的母线8处接有双馈风机。图12给出三种工况下的关键母线的暂态电压波形，求得的区域暂态电压失稳风险指如表5所示。
[0146]
表5相同容量电动机接入不同位置时区域暂态电压稳定性指标
[0147][0148]
从表5的计算结果可以看出，随着异步电动机接入位置距风机距离的增大，区域暂态电压失稳风险指标在降低，系统的暂态电压稳定性在提高，图12所示的关键母线的暂态电压波形也得以体现该特点。
[0149]
3)负荷功率突增扰动：
[0150]
当双馈风机于母线8处并网运行，0.1s时区域内所有负荷的有功功率、无功功率同时增加21kw、21kvar，表6针对负荷功率突增，对比了风电渗透率的大小与区域暂态电压安全裕度指标、区域暂态电压失稳风险指标的关系。三种渗透率下的关键母线暂态电压波形如图13所示。
[0151]
表6负荷功率突增时区域暂态电压稳定性指标
[0152][0153]
表6和图13共同说明了区域风电渗透率越高，该区域承受负荷突增扰动的能力就越强，暂态电压稳定性也就越好。
[0154]
当负荷突增功率的总容量不变时，区域暂态电压安全裕度会随着各负荷突增容量的大小不同而不同，表7依据负荷距风机电气距离的远近对两种预设工况进行仿真分析，仿真结果如图14和表8所示。
[0155]
表7系统内负荷的突增情况
[0156][0157]
表8不同负荷突增情况下的区域暂态电压稳定性指标
[0158][0159]
由图14和表8的计算结果可知，负荷距离风机越近，负荷功率突增对区域暂态电压稳定性的影响越小，同时也意味着这些近端的负荷所能允许的突增容量大于那些远端负荷。
[0160]
4)负荷功率突减扰动：
[0161]
表9和图15对应了0.1s时系统内所有负荷的有功功率、无功功率同时减少21kw、 21kvar时的仿真结果。
[0162]
表9负荷功率突减时区域暂态电压稳定性指标
[0163][0164]
可见，同负荷突增一样，在面对负荷突减扰动时，风电渗透率越大，系统承受负荷扰动的能力越强，暂态电压稳定性越好。
[0165]
同理，根据负荷距风机电气距离的远近，对表10所示的两种工况进行仿真分析，结果如图16和表11所示。
[0166]
表10系统内负荷的突减情况
[0167][0168]
表11不同负荷突减情况下的区域暂态电压稳定性指标
[0169][0170]
由仿真结果可得：负荷功率突减的瞬间区域母线电压被抬升，此时该区域面临过电压失稳的风险，且当负荷功率突减总量不变时，负荷距风机越远，负荷功率突减造成的区域过电压风险越大，系统的暂态电压稳定性越差。
[0171]
综上所述，基于所提指标的评估结果总能确切表现实际系统的暂态电压稳定水平，精准地量化各母线电压的稳定程度，为后续无功补偿装置的配置提供了理论支撑。