利用超分辨成像对单分子定量的方法与流程

t w 1978),5.直方图形状(doyle w 1962，guo r and pandit s m 1998，prewitt j m and mendelsohn m l 1966),6.直方图熵信息(jui-cheng yet al 1995，kapur j net al 1985，li c h and lee c k 1993，li c h and tam p k s 1998，pun t 1980，shanbhag a g 1994),和7.其它变异类型(zack g wet al 1977)。
5.我们前期的研究表明，现有的常规fiji(imagej)(schneider c aet al 2012) 处理手段已经不再适用于超分辨影像的分子分割(图1和2)，需要更好的分割算法。近期研究表明，利用深度学习的单分子分割要比阀值处理的隐马模型具有更好的效果(li jet al 2020)。可见，基于量子点的单分子成像，结合超分辨技术和单分子分割方法，形成的超分辨单分子影像，将使单分子分析将从常规的计数向高维度转变，进而促进了疾病相关的生物标记物研究。
6.现有单分子检测技术的三个明显局限：(1)关于平均值的整体信息； (2)需要使用校准或内部参考的相对定量；(3)由于光学分辨率的限制，传统的荧光显微镜在精确计数方面具有严重缺陷。它们的灵敏度不足限制了其广泛的应用，尤其是低丰度目标的测量方面。光学成像的定量化方法中，深度学习过于繁杂，而传统阀值方法又不能兼顾灵敏性和鲁棒性。


技术实现要素：

7.本发明的目的在于提供一种纳米级分割，允许在分子水平上分析“超分辨的单分子影像”而无需校准，能够克服了所有上述限制，极大地促进了高灵敏单分子检测的进展。
8.为实现以上目的，本发明通过以下技术方案予以实现：
9.对成像数据归一化处理后，利用空间分辨率对该数据设定连通体的大小，
10.再利用熵的变异类函数衡量连通体的表征参数，求得极大值。
11.有益效果：
12.通过该方法的处理，实现更真实地显像和更准确地定量化。
附图说明
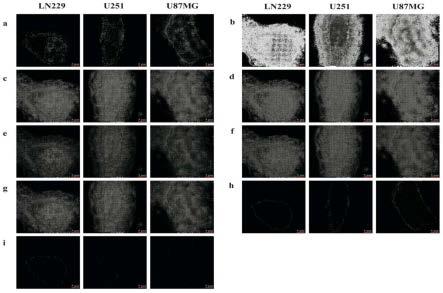
13.图1为各类局部tms用来处理三类细胞系的三维sim数据的最中间一层示意图；
14.图2为普适的ccce和全局tms用来处理三类细胞系的三维sim数据的最中间一层示意图。
15.图3为凝聚层级聚类(左)和分子表达定量化的示意图。
16.图4为各方法的准确度、敏感度、特异度和rmsd的示意图。
具体实施方式
17.为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
18.对成像数据归一化处理后，利用空间分辨率对该数据设定连通体的大小，再利用熵的变异类函数衡量连通体的表征参数，求得极大值。通过该方法的处理，实现更真实地显
像和更准确地定量化。
19.设m是维度为(d1,d2,d3...dn)且连接度分别为(c1,c2,c3...cn)的高度数组，即，cn代表在维度dn的分辨率，m(d1,d2,
…dn
)代表数组在位置 (d1,d2,
…dn
)的大小。考虑到通用性，我们对成像数据做归一化处理，公式如下：
[0020][0021]
这里，l是常数，符号[]代表四舍五入操作符。在我们的计算工作中，设l＝255，m
min
和m
max
分别代表数组m(d1,d2,
…dn
)的最大和最小值。
[0022]
为了简化表达，令nc代表以下常量：
[0023][0024]
为了抽取数组特征，卷积处理如下：
[0025][0026]
且
[0027][0028]
这里k是卷积内核，大小为(c1,c2,c3,...cn)，值皆为1/nc；g和b 分别是梯度数组和二值化数组。位置(d1,d2,
…dn
)处g的取值是g，成员函数i(d1,d2,
…dn
)返回大小为(c1,c2,c3,...cn)的邻近空间中满足梯度值大小g的空间位置，而m
min
则代表这些成员中最小的灰度值。
[0029]
基于shannon函数
[0030][0031]
这里(ξ)＝1且β(ξ)＝n。重新定义如下成员函数：
[0032]
α(ξ)＝ξnc[0033][0034]
[0035]
这里成员函数γ(g,i)表明，b
(g)
中，当梯度值为g且连通度为nc-1时，邻近成员数为i的连通体的数目。该成员函数可以看作特征函数，代表了颗粒度。因此，我们得到了，基于临界分辨率且有两个变量g和ξ的熵函数，并把这个熵称为，临界连通熵(connected-component entropy,ccce)。类似于信息熵，但略有变形。
[0036]
在我们的实验中，我们察觉到，当把ξ设为2，则单变量熵函数e(g) 规律且稳健地变化如s形曲线。让e
max
和e
min
代表s形变化过程中的最大和最小值，e-1
(e)代表e(g)的反函数，则可得到梯度阈值函数h(θ)如下
[0037]
h(θ)＝e-1
(e
min
)+θ(e-1
(e
max
)-e-1
(e
min
))
[0038]
这里0《θ《1，确定了分离系数θ后我们可以得到临界值h(θ)，即梯度的阈值和相关的二值化数组b(g)，二值化数据代表了前景色或空间对象。我们的实验中，θ＝0.75取得了最好的纳米组分割，不过我们推荐θ＝0.5做一般的分割处理。
[0039]
如图1-4所示，现有的常规fiji(imagej)(schneider c aet al 2012)处理手段已经不再适用于超分辨影像的分子分割(图1和2)。正如图4所示，提出的新方法ccce具有最高的准确度，表现出最好的量化表征(图3)和相对不错的敏感度与特异度。正如定量分析所揭示的，phansalkar和moments 过高地表征了分子表达的信号量；yen、renyientropy和maxentropy在定量分析和分子图谱的轮廓分析中皆表现出很差的敏感度；除了定量分析中差强人意的敏感度和稳健性，sauvola由于方法自身的问题，在分子图谱中导致了极差的敏感度。总体而言，可以得出结论，ccce在定性和定量评估中，表现最佳。
[0040]
以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。