一种考虑结构和气动非线性的飞行动力学建模方法

1.本发明属于无人机技术领域，具体涉及一种考虑结构和气动非线性的飞行动力学建模方法，可以用于考虑结构和气动非线性的飞行动力学建模。


背景技术：

2.高空长航时飞机为降低重量、提高升阻比，使用轻质、各向异性材料，机翼细长，具有柔性。结构大变形、气动失速和结构低频振动与刚体运动耦合，是高空长航时柔性飞机在常规低速飞行状态下的普遍现象，显著影响其气动弹性和飞行动力学特性。高空长航时无人机具有极其重要的应用价值和发展潜力。但面对苛刻的飞行任务要求，应用新技术以扩大设计空间的同时，创新性的设计方案却引发出新的问题。这些新问题，概括起来，主要表现在如下三个方面：
3.(1)结构几何非线性：为获得低重量和高升阻比，普遍使用复合材料等轻质材料，且采用大展弦比设计，结构细长，导致结构具有柔性，甚至大柔性的特点。结构几何非线性将导致结构静、动态特性和气动载荷分布等的改变，进而影响气动弹性特性。
4.(2)气动力非线性：高空低速飞行时，局部攻角较大，且受结构大变形影响，更易于发生气动失速，出现流动分离；而在高空高亚音速飞行时，使用层流翼型，易于产生跨音速激波，出现流动分离。结构几何非线性与气动力非线性的耦合，将导致新的非线性气动弹性特性。
5.(3)结构弹性运动与全机刚体运动的耦合：飞翼布局是这一问题的典型代表，柔性结构固有频率很低时，将与刚体运动发生耦合，可能导致不稳定运动模态或较低刚体自由颤振速度，为方案设计带来不利影响。
6.面对这三方面主要因素，研究者们意识到在涉及气动弹性的多学科新问题上理论基础与分析手段的不足——尤其体现在helios原型机失事和飞翼/连翼布局传感器飞机研究上。因此，针对以高空长航时无人机为代表的柔性飞机，开展考虑结构和气动非线性的飞行动力学建模研究十分必要。


技术实现要素：

7.本发明属于无人机技术领域，具体涉及一种考虑结构和气动非线性的飞行动力学建模方法，通过耦合非线性结构模型和非线性气动模型，建立考虑结构和气动非线性的飞行动力学模型。
8.为了实现以上发明目的，本发明采取的技术方案如下：
9.一种考虑结构和气动非线性的飞行动力学建模方法，包括以下步骤：
10.步骤1、将无人机结构三维梁问题解耦为非线性梁运动分析和梁截面变形分析，建立无人机非线性结构模型；
11.步骤2、基于气动降阶模型建立无人机非线性气动模型；
12.步骤3、通过无人机非线性结构模型与无人机非线性气动模型的耦合，建立无人机
气动弹性模型；
13.步骤4、将重力载荷和气动力载荷的贡献项以及边界条件项，代入到无人机非线性气动弹性模型，得到柔性飞机气动弹性与飞行动力学耦合模型；
14.步骤5、基于newton
‑
raphson方法求解柔性飞机非线性气动弹性与飞行动力学耦合模型的静平衡解，采用generalized
‑
α算法求解非线性时域响应。
15.进一步的详细步骤为：
16.步骤1、考虑剪切变形和翘曲变形，基于有限元离散，构建表征剖面特性的刚度矩阵，建立二维梁剖面模型。通过非连续协调方程表征节点质量等不连续因素，结合二维梁剖面模型和几何精确本征梁理论建立非线性梁结构模型，从而建立无人机非线性结构模型。
17.步骤2、建立结构实体模型，对该结构模型进行模态分析。得到各阶模态向量和结构节点坐标。基于结构节点坐标和对应的模态向量通过差值可以得到气动节点坐标对应的各阶模态位移向量，从而用于非定常气动力的节点位移输入。建立结构几何外形以及外部流场几何形状，将该几何导入流体网格绘制软件中绘制气动网格，导入计算流体力学软件中计算，设置压力远场条件。机翼表面设置为无滑动静态壁面条件，网格在翼型附近被细化。采用动态网格结合用户自定义函数接口编程，采用弹簧方法进行网格重构实现机翼的模态位移连续变形。在数值计算中，采用双精度求解器进行数值模拟，采用spalart
‑
allmaras湍流模型。采用广义位移输入，计算广义气动力，基于气动降阶模型建立二者的非线性关系，最终得到无人机非线性气动模型。
18.步骤3、将重力载荷贡献项、气动力载荷贡献项，边界条件项，以及连续条件项代入梁结构离散化方程中，最终得到梁结构的无人机气动弹性模型：
[0019][0020]
其中下标stru,aero,grav分别表示结构、气动、重力，m、q、f表示刚度矩阵、状态变量、载荷。其中m
stru,aero
表示气动载荷对结构状态方程中一阶变量的影响项，可由气动力方程中推导得出，m
aero,stru
表示结构运动对气动状态方程中一阶变量的影响项，可由气动和结构耦合方程中推导得出。
[0021]
步骤4、考虑气动弹性与飞行力学的耦合效应，在参考原点引入集中质量，引入刚体质点运动方程
[0022][0023][0024]
其中m
rigid
和i
rigid
为刚体质点的质量矩阵和转动惯量矩阵，v
rigid
和ω
rigid
为其运动的线速度和角速度，f
rigid
和m
rigid
为作用在其上的力和力矩。
[0025]
步骤5、耦合柔性梁的气动弹性方程和刚体质点的飞行力学方程，将其简单表示为
[0026][0027]
式中，q为由结构状态和气动状态等变量组成的未知列向量，矩阵m
coup
和列向量f
coup
均为未知向量q的函数。
[0028]
系统方程的静平衡解q0，可通过newton
‑
raphson迭代算法求解非线性代数方程组
[0029]
f
coup
(q0)＝0
[0030]
获得。
[0031]
为了提高计算效率，优选的，利用控制相对/绝对误差和迭代步数来实现自适应步长的newton
‑
raphson算法迭代求解其静态平衡状态。系统方程的动态时域响应，可采用generalized
‑
α算法进行求解，在时间步进时，以前一时刻作为当前时刻的初始猜测，求解出当前时刻的状态。计算中根据迭代收敛速度调整时间步进长度，实现变步长时域积分。
[0032]
本发明提供了一种考虑结构和气动非线性的飞行力学建模方法，能准确模拟高空长航时柔性飞机结构大变形、气动失速和结构低频振动与刚体运动耦合现象，分析其气动弹性和飞行动力学特性，为高空长航时柔性飞机设计提供重要理论支撑，具有重要的应用价值。
附图说明
[0033]
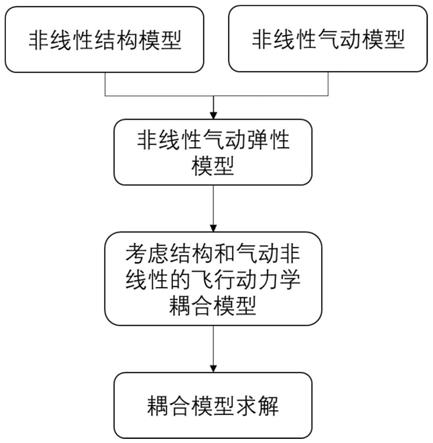
图1是本发明方法流程图；
[0034]
图2是实施例的柔性飞机布局示意图纵向运动模态根轨迹图；
[0035]
图3是实施例的柔性飞机配平状态下全机静变形；
[0036]
图4是实施例的柔性飞机满载时的时间历程。
具体实施方式
[0037]
为使本发明的目的、技术方案及优点更加清楚明白，以下根据附图并列举实施例，对本发明做进一步详细说明。
[0038]
如图1所示，一种考虑结构和气动非线性的飞行动力学建模方法，包括以下步骤：
[0039]
步骤1、将无人机结构三维梁问题解耦为非线性梁运动分析和梁截面变形分析，建立无人机非线性结构模型；
[0040]
步骤2、基于气动降阶模型建立无人机非线性气动模型；
[0041]
步骤3、通过无人机非线性结构模型与无人机非线性气动模型的耦合，建立无人机非线性气动弹性模型；
[0042]
步骤4、将重力载荷和气动力载荷的贡献项以及边界条件项，代入到无人机非线性气动弹性模型，得到柔性飞机非线性气动弹性与飞行动力学耦合模型；
[0043]
步骤5、基于newton
‑
raphson方法求解柔性飞机非线性气动弹性与飞行动力学耦合模型的静平衡解，采用generalized
‑
α算法求解非线性时域响应。
[0044]
进一步的详细步骤为：
[0045]
步骤1、考虑剪切变形和翘曲变形，基于有限元离散，构建表征剖面特性的刚度矩阵，建立二维梁剖面模型。通过非连续协调方程表征节点质量等不连续因素，结合二维梁剖面模型和几何精确本征梁理论建立非线性梁结构模型，从而建立无人机非线性结构模型。
[0046]
步骤2、建立结构实体模型，对该结构模型进行模态分析。得到各阶模态向量和结构节点坐标。基于结构节点坐标和对应的模态向量通过差值可以得到气动节点坐标对应的各阶模态位移向量，从而用于非定常气动力的节点位移输入。建立结构几何外形以及外部流场几何形状，将该几何导入流体网格绘制软件中绘制气动网格，导入计算流体力学软件中计算，设置压力远场条件。机翼表面设置为无滑动静态壁面条件，网格在翼型附近被细
化。采用动态网格结合用户自定义函数接口编程，采用弹簧方法进行网格重构实现机翼的模态位移连续变形。在数值计算中，采用双精度求解器进行数值模拟，采用spalart
‑
allmaras湍流模型。采用广义位移输入，计算广义气动力，基于气动降阶模型基于气动降阶模型建立二者的非线性关系，最终得到非定常非线性气动力模型。
[0047]
步骤3、将重力载荷贡献项、气动力载荷贡献项，边界条件项，以及连续条件项代入梁结构离散化方程中，最终得到梁结构的无人机气动弹性模型：
[0048][0049]
其中下标stru,aero,grav分别表示结构、气动、重力，m、q、f表示刚度矩阵、状态变量、载荷。其中m
stru,aero
表示气动载荷对结构状态方程中一阶变量的影响项，可由气动力方程中推导得出，m
aero,stru
表示结构运动对气动状态方程中一阶变量的影响项，可由气动和结构耦合方程中推导得出。
[0050]
步骤4、考虑气动弹性与飞行力学的耦合效应，在参考原点引入集中质量，引入刚体质点运动方程
[0051][0052][0053]
其中m
rigid
和i
rigid
为刚体质点的质量矩阵和转动惯量矩阵，v
rigid
和ω
rigid
为其运动的线速度和角速度，f
rigid
和m
rigid
为作用在其上的力和力矩。
[0054]
步骤5、耦合柔性梁的气动弹性方程和刚体质点的飞行力学方程，将其简单表示为
[0055][0056]
式中，q为由结构状态和气动状态等变量组成的未知列向量，矩阵m
coup
和列向量f
coup
均为未知向量q的函数。
[0057]
系统方程的静平衡解q0，可通过newton
‑
raphson迭代算法求解非线性代数方程组
[0058]
f
coup
(q0)＝0
[0059]
获得。为了提高计算效率，本文利用控制相对/绝对误差和迭代步数来实现自适应步长的newton
‑
raphson算法迭代求解其静态平衡状态。系统方程的动态时域响应，可采用generalized
‑
α算法进行求解，在时间步进时，以前一时刻作为当前时刻的初始猜测，求解出当前时刻的状态。计算中根据迭代收敛速度调整时间步进长度，实现变步长时域积分。
[0060]
以一常规布局高空长航时柔性飞机为例，考虑分析包括全机配平和纵向动稳定性，布局如图2所示。其翼展为72.78m，外翼有10
°
上反角；弦长为2.438m，根稍比为1；展向对称布置5个发动机和3个吊舱，其中，左右两侧吊舱质量为22.68kg，翼展中心处吊舱用于装载有效载荷，质量为27.22kg(空载)～254.0kg(满载)。
[0061]
如图3所示为柔性飞机配平状态下全机静变形，图4为考虑失速和不考虑失速状态柔性飞机满载时的时间历程，在发生失速的响应过程中，失速区域局限于翼尖附近。全机升力损失较小(在当前计算时间范围内)，考虑失速和不考虑失速的两种响应结果没有明显区别。