用于桩基在爆炸动荷下稳定分析的解析计算方法

1.本发明涉及一种计算解析方法，尤其是一种用于桩基在爆炸动荷下稳定分析的解析计算方法。


背景技术：

2.燃气爆炸在建筑物底层或地下室发生时对桩基造成结构损伤，而这种桩基损伤不易直观发现，其对上部结构建筑将来埋下安全隐患。现有技术中，对桩基在爆炸动荷下稳定分析的解析计算方法准确度很低，鉴于此，我们提出一种用于桩基在爆炸动荷下稳定分析的解析计算方法。


技术实现要素：

3.本发明的一个目的是通过提出一种用于桩基在爆炸动荷下稳定分析的解析计算方法，以解决上述背景技术中提出的缺陷。
4.本发明采用的技术方案如下：包括推导单桩动力学方程和建立单桩力学模型。
5.所述建立单桩力学模型包括建立爆炸荷载q1，上部结构的简化质量块m0，爆炸荷载作用的范围h，及计算桩顶的竖向荷载p。
6.所述建立单桩力学模型还包括采用双参数地基模型来计算土层中地基的反力。上述双参数模型计算如下：
[0007][0008]
其中，k＝m0b1，g
p
＝gb1，m0为桩侧土体的抗力系数，b1为计算宽度，当桩径d≥1时，b1＝0.9(d+1)；当d＜1时，b1＝0.9(1.5d+0.5)，g为土体的剪切刚度，表达式为：
[0009][0010]
其中，ν
s
为地基土的泊松比，e
s
为地基土的弹性模量，h
g
为地基土的剪切层厚度。
[0011]
作为本发明技术方案的进一步改进：所述单桩力学模型的位移为：
[0012]
u(x,z,t)＝u0(z,t)
‑
zw
,x
(z,t)
[0013]
w(x,z,t)＝w0(z,t)
[0014]
考虑几何非线性应变分量可表示为：
[0015][0016]
其中，ε
z
为z向应变；w
x
为x向位移；α为参数因子，当α＝0时，即为不考虑几何非线性；当α＝1，表示考虑几何非线性。
[0017]
作为本发明技术方案的进一步改进：所述单桩力学模型由本构方程与应力、内力之间的关系有：
[0018][0019]
m＝eiw
，zz
[0020]
其中，m为桩身内的弯矩，n为桩身轴力，e为桩身弹性模量，a为桩身截面积，i为桩身截面惯性矩；
[0021]
作为本发明技术方案的进一步改进：所述建立单桩动力学方程包括：
[0022]
采用求解超静定结构支座反力的方式来计算桩顶铰支座处反力：
[0023][0024]
取任意时刻桩身任意z截面的上部进行分析，考虑桩身z方向的受力平衡，可得平衡方程式：
[0025][0026][0027]
其中，θ为沿桩身z方向截取的长度变量，对z方向求二阶导；
[0028]
根据桩身位移边界条件可得式：
[0029]
z＝0,w(0,t)＝0,w
,z
(0,t)＝0,u(0,t)＝0
[0030][0031]
假设桩身在受到爆炸荷载之前为静止状态，则方程的初始条件为：
[0032][0033]
所述方程采用伽辽金方法和龙格
‑
库塔法相结合的方式来求解；
[0034]
首先假设方程有如下形式的函数解：
[0035][0036][0037]
这两个假设形函数的解满足上述位移边界条件式，将这两个函数解代入至上式中可得：
[0038][0039][0040]
将上式采用伽辽金方法处理，可得如下仅含有时间变量的非线性动力微分控制方程：
[0041][0042][0043]
其中，α1～α3，β1～β4为通过伽辽金方法积分后所得的微分方程的系数，具体计算公式如下所示：
[0044][0045][0046][0047][0048]
[0049][0050][0051]
对上式进行数值计算，得到u和w的数值解，然后将其代回至假设的函数解中，得到桩身的位移响应函数u(z,t)，w(z,t)，该部分的数值计算部分采用四阶龙格
‑
库塔方法进行计算，得到桩身的位移响应函数，根据b
‑
r准则，绘制出桩身的位移时程曲线。结构在微小冲击作用增量下引起剧烈响应增量，则认为结构发生屈曲失稳破坏；
[0052]
上述四阶龙格
‑
库塔方法先计算以下四个数：
[0053][0054]
上式，δt为计算步长，由下式计算：
[0055][0056]
本发明推导了桩基在爆炸荷载作用下的稳定性方程，并进行求解。即建立了一种用于桩基在爆炸动荷下稳定分析的计算解析方法，并通过计算机数值仿真模型验证了解析方法的正确性。同时对影响桩基稳定的参数进行了敏感性分析。本发明建立的方法便于操作可行而且高效准确。
附图说明
[0057]
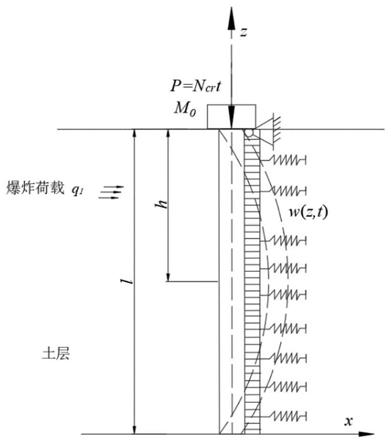
图1为本发明优选实施例的桩
‑
土模型图；
[0058]
图2为本发明优选实施例的材料应力
‑
应变曲线图；
[0059]
图3为本发明优选实施例的桩身部分结构计算模型图；
[0060]
图4为本发明优选实施例的桩
‑
土模型边界条件设置图；
[0061]
图5为本发明优选实施例的土体模型网格划分图；
[0062]
图6为本发明优选实施例的桩身模型网格划分图；
[0063]
图7为本发明优选实施例的有限元解与理论解对比图；
[0064]
图8为本发明优选实施例的随爆炸荷载增加桩身位移时程曲线变化图；
[0065]
图9为本发明优选实施例的桩径d变化对桩身位移
‑
时程曲线的影响图；
[0066]
图10为本发明优选实施例的两种地基模型对比下桩身位移
‑
时程曲线图；
[0067]
图11为本发明优选实施例的桩身位移
‑
时程曲线随桩侧土体参数k增加的变化图；
[0068]
图12为本发明优选实施例的桩身失稳荷载随桩侧土体抗力系数k增加的变化图；
[0069]
图13为本发明优选实施例的桩顶等效质量块m0对桩身位移
‑
时程曲线的影响图。
具体实施方式
[0070]
需要说明的是，在不冲突的情况下，本实施例中的实施例及实施例中的特征可以相互组合，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0071]
实施例1：
[0072]
本发明优选实施例提供了一种用于桩基在爆炸动荷下稳定分析的解析计算方法，
[0073]
单桩力学模型简化图如图1
‑
13所示，其中q1为爆炸荷载，p为桩顶的竖向荷载，m0为上部结构的简化质量块，h为爆炸荷载作用的范围。土层中地基的反力采用双参数地基模型来计算，将土体的反力简化为互不影响的线性弹簧，同时考虑剪切作用的影响，l为土层的厚度，w(z,t)为桩身的横向位移，u(z,t)为桩身的竖向位。
[0074]
土层中地基的反力采用双参数地基模型计算，由于传统的winkler模型仅由一个参数描述土体，没有考虑土体之间的连续性影响，而双参数模型是由两个参数来描述土体的状态，不仅将土体的反力化为互不影响的线性弹簧，同时还同时考虑剪切作用的影响，相比于winkler模型更加符合土体的实际状态。因此本文选择采用双参数模型来计算地基反力。
[0075]
具体的双参数模型计算如下式所示：
[0076][0077]
式(1)中，k＝m0b1，g
p
＝gb1，m0为桩侧土体的抗力系数，g为土体的剪切刚度，b1为计算宽度。当桩径d≥1时，b1＝0.9(d+1)；当d＜1时，b1＝0.9(1.5d+0.5)。
[0078]
g为土体的剪切刚度，表达式为：
[0079][0080]
式(2)中，ν
s
为地基土的泊松比，e
s
为地基土的弹性模量，h
g
为地基土的剪切层厚度。依据申请人的研究结果，本实施例取11倍的桩径作为地基土的剪切层厚度。
[0081]
图1模型中的位移可表达为下式：
[0082]
u(x,z,t)＝u0(z,t)
‑
zw
,x
(z,t)
ꢀꢀꢀ
(3)
[0083]
w(x,z,t)＝w0(z,t)
ꢀꢀꢀ
(4)
[0084]
考虑几何非线性应变分量可表示为：
[0085][0086]
式(5)中，ε
z
为z向应变；w
x
为x向位移；α为参数因子，当α＝0时，即为不考虑几何非线性；当α＝1，表示考虑几何非线性。
[0087]
材料的应力
‑
应变关系如图2所示。
[0088]
σ＝e
e
ε，仅考虑弹性本构，即σ＜σ
s
。
[0089]
此时e
e
≡e。
[0090]
由本构方程与应力、内力之间的关系有：
[0091][0092]
m＝eiw
,zz
ꢀꢀꢀ
(7)
[0093]
式(6)、(7)中，m为桩身内的弯矩，n为桩身轴力，e为桩身弹性模量，a为桩身截面积，i为桩身截面惯性矩。
[0094]
桩顶铰支座处反力可以采用求解简单超静定结构支座反力的方式来计算，如式(8)所示：
[0095][0096]
取任意时刻桩身任意z截面的上部进行分析，考虑桩身z方向的受力平衡，可得平衡方程式(9)：
[0097][0098][0099]
式(9)、(10)中，θ为沿桩身z方向截取的长度变量，对z方向求二阶导。
[0100]
根据桩身位移边界条件可得式：
[0101]
z＝0,w(0,t)＝0,w
,z
(0,t)＝0,u(0,t)＝0
ꢀꢀꢀ
(11)
[0102][0103]
假设桩身在受到爆炸荷载之前为静止状态，则方程的初始条件为：
[0104][0105]
上述非线性微分方程可采用伽辽金方法和龙格
‑
库塔法相结合的方式来求解。
[0106]
首先假设方程有如下形式的函数解：
[0107][0108]
[0109]
这两个假设形函数的解满足上述位移边界条件式，将这两个函数解代入至式(9)、(10)中可得：
[0110][0111][0112]
将式(16)、(17)采用伽辽金方法处理，可得如下仅含有时间变量的非线性动力微分控制方程：
[0113][0114][0115]
式(18)、(19)中，α1～α3，β1～β4为通过伽辽金方法积分后所得的微分方程的系数，具体计算公式如下所示：
[0116][0117][0118]
[0119][0120][0121][0122][0123]
对式(18)、(19)进行数值计算，得到u和w的数值解，然后将其代回至假设的函数解(14)、(15)中，得到桩身的位移响应函数u(z,t)，w(z,t)。该部分的数值计算部分采用四阶龙格
‑
库塔方法进行计算，得到桩身的位移响应函数，根据b
‑
r准则，绘制出桩身的位移时程曲线。结构在微小冲击作用增量下引起剧烈响应增量，则认为结构发生屈曲失稳破坏。
[0124]
利用四阶龙格
‑
库塔方法的技巧在于递求x
n+1
。该方法先计算以下四个数：
[0125][0126]
式(27)中，δt为计算步长，由下式计算:
[0127][0128]
四阶龙格
‑
库塔方法通常给出精确解而不要过小的步长δt。
[0129]
本实施例采用ansys/ls
‑
dyna有限元软件建模进行分析，验证理论解的正确性。
[0130]
桩身和土体模型单元均采用三维实体单元，单元类型为c3d8r，减缩积分，沙漏控制，总单元数为50458；模型尺寸中取桩长l为45m，桩径d为2m，土体模型为60m
×
60m
×
60m的
立方体。
[0131]
参数选取为：桩身弹性模量，泊松比为0.2，桩身完全嵌入土体，ρ＝2.6
×
103kg/m3；模型边界条件设置为底端固定，x方向限制x方向的位移，y方向限制y方向的位移；燃气爆炸荷载均通过计算后直接施加到桩身的相应位置处。桩土界面处设置接触，为真实地模拟桩
‑
土之间的相互作用关系，使得软件的计算过程能更快地收敛，在划分有限元模型网格时，将距离桩体较近的网格单元划分得更密更精准，距离桩身单元较远的网格单元划分相对较为稀疏。这样的网格划分有助于提高数值分析精度并加快有限元计算过程的收敛速度。有限元模型的荷载施加和网格划分具体如图4、图5和图6所示。
[0132]
图7显示，有限元解与理论解误差仅为3％～6％，吻合较好，验证了理论解的正确性。其后将采用前述理论进行公式推导，针对影响桩身稳定性影响因素进行参数分析。
[0133]
取自实际工程的分析具有实用性。桩长取15m，桩径d为1.2m，爆炸荷载以矩形荷载的形式施加至桩身上，土体模型采用双参数地基模型
‑
pasternak地基模型计算桩侧土体的抗力。
[0134]
根据前述推导得到的函数方程，通过代入上述参数进行计算即可得到桩身的位移
‑
时程曲线。图8中的q1为爆炸荷载。随着爆炸荷载不断增加，桩身位移时程曲线随之变化。当爆炸荷载q1较小时，桩身做简谐运动；随着q1增加，桩身简谐运动的位移逐渐增大，当爆炸荷载q1增大到1520kn时，桩身开始失稳，图8中曲线显示，桩身位移时程曲线趋向无穷大。根据b
‑
r准则可以确定此时桩身已经失稳，其对应的荷载即为此时的失稳荷载。当荷载达到失稳荷载后，桩身失稳的速度非常快，桩身的位移在短时间内迅速增加，给结构带来极大的安全隐患。在具体的工程设计中要尽量避免出现失稳荷载。
[0135]
图9为桩身位移时程曲线随桩径d增加的变化曲线。图9显示，当桩径d较小时，桩
‑
土体系的整体刚度较小，桩身在很小的爆炸荷载作用下，桩身发生失稳。随着桩径d不断增大，桩身刚度逐渐增大，桩身与桩侧土体的接触面积亦随之增大，桩侧土体的抗力作用增大，整个桩
‑
土体系稳定性增大。在相同的荷载作用下，桩身不再失稳，桩身位移趋于平稳且开始做简谐运动。随着桩径d进一步增大，桩身位移继续减小，随着d增加，桩身简谐运动周期开始增大。说明随着d增加，桩
‑
土体系稳定性大大增加，桩身越来越趋于稳定状态，这有利于整个桩基的安全性。
[0136]
在一定条件下增加桩径d可以有效地提高桩身稳定性能。
[0137]
图10为双参数地基模型计算下的桩身位移曲线与winkler模型计算下的桩身位移曲线对比。图10显示，两种地基模型区别较为明显。在相同爆炸荷载作用下，当采用双参数地基模型进行计算时，桩身位移较小，桩身做简谐运动周期较小.当采用winkler模型计算时，桩身位移相对较大，且桩身简谐运动周期较大。当荷载增大到失稳荷载时，采用双参数地基模型计算，相应桩身失稳荷载比采用winkler模型计算时大，这表明采用双参数地基模型计算所得到的结果更加安全。双参数模型考虑了土体剪切模量的影响，较winkler模型更加符合工程实际。
[0138]
图11显示，随着桩侧土体抗力系数增大，在相同爆炸荷载作用下，桩身位移逐渐减小；随着k增加，桩身简谐运动周期逐渐减小。这表明桩侧土体参数对于桩身位移和稳定有重要作用。图12显示，桩侧土体抗力系数k对桩身失稳荷载的影响，随着k不断增加，桩身失稳荷载亦随之不断增大；随着k增大，桩身失稳时间也随之提前。桩侧土体抗力系数k对于整
个桩身稳定性作用显著，说明桩侧土体对于整个桩身稳定十分重要。
[0139]
图13显示，随着桩顶等效质量块m0增加，桩身位移曲线首先降低。随桩顶质量增加，在一定程度上可以抑制桩身侧向位移；当m0继续增大时，整个桩身不稳定性增加，在同一个爆炸荷载作用下，桩身位移急剧增大，桩身开始失稳，如图13中虚线所示。在一定桩身柔度下，适当地增加桩顶质量可以提高桩身稳定性，当桩顶质量增加过大，则可能导致桩身失稳，给结构带来巨大的安全隐患。在实际工程的桩基设计时要格外注意桩顶的等效质量对其稳定性的影响。
[0140]
本实施例研究在爆炸荷载作用下桩基动力稳定性。采用双参数地基桩土模型同时考虑剪切作用，相比于winkler模型更加符合土体的实际状态。
[0141]
采用伽辽金积分方法和四阶龙格库塔方法相结合的方式求解桩身的非线性动力稳定方程，同时得到桩身的位移时程曲线，利用b
‑
r准则可以得到相应的桩身失稳荷载，利用软件ansys/ls
‑
dyna15.0软件进行模拟验证理论解的正确性，最后根据理论公式对其桩身稳定的影响参数进行分析。随爆炸冲击荷载不断增大，桩身位移逐渐增大，当达到失稳荷载后，桩身位移会迅速增大，桩身发生失稳；桩侧(岩)土体抗力系数k对与提高桩身稳定性有重要作用，通过增大k值可以有效地降低桩身位移幅值，减小桩身简谐运动周期。采用本模型计算所得到的桩身位移时程曲线幅值比传统winkler模型计算值更小，同时对应得到的桩身失稳荷载更大，更吻合实际工程。在一定桩身柔度范围内，随着桩顶等效质量块增加，桩身位移幅值降低，随着质量不断增大，超过某个限值时，在爆炸冲击荷载作用下，桩身位移急剧增大，桩身发生失稳。
[0142]
本实施例为实际工程在爆炸荷载作用下桩基动力稳定的计算分析以及设计提供了一种方便有效的方法。
[0143]
对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内。不应将权利要求中的任何附图标记视为限制所涉及的权利要求。
[0144]
此外，应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施例中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。