基于DNA链交换和扩散的图像加密算法

基于dna链交换和扩散的图像加密算法
技术领域
1.本发明属于信息处理及数据加密技术领域，具体涉及基于dna链交换和扩散的图像加密算法。


背景技术：

2.与文本信息相比，图像信息可以携带更多而且更加直观的信息，因此人们可以从图片中获取信息的方式较文本更加方便和快捷，对于媒体、医疗及军事通讯等领域，图像的存储、传输和接收非常重要，可以说21世纪既是一个信息时代，也是一个读图的时代，随之而来的是信息的泄露和破解对于个人财产及隐私甚至国家安全构成巨大的威胁，因此确保图像信息安全具有重要的意义；
3.一般的混沌图像加密包含图像置乱和像素扩散两个环节，其中图像置乱通过改变明文图像像素的位置，达到图像置乱的效果，但这一操作并不能改变明文图像像素值的大小，也不能掩盖相邻像素间的关系，另一操作为扩散环节，这一操作可以改变明文图像的像素值，并大幅减弱相邻像素间的关联度，提高加密图片的信息熵；
4.不可否认的是：目前大多数混沌图像加密算法只是单一的图像像素值置乱或位置置乱且使用上述任何一种以上的方式都无法确保图像具有较高的安全性；
5.基于以上，本发明提供一种基于dna链交换和扩散的图像加密算法。


技术实现要素：

6.针对上述情况，为克服现有技术之缺陷，本发明提供一种基于dna链交换和扩散的图像加密算法，本方案中dna链交换不仅可以改变像素的位置，也可以改变像素值，并且本方案中的dna链的扩散是一种条件性扩散，条件性扩散在加密过程中容易执行，但条件性扩散的消除过程是困难的，因此本发明的加密方法能更好的确保图像的信息安全。
7.基于dna链交换和扩散的图像加密算法，其特征在于，包括以下步骤：
8.s1：构造改进的动态帐篷耦合映射格子
[0009][0010]
s2：秘钥生成
[0011]
(1)利用明文像素值p(i,j)，得到以二进制数k
[0012][0013]
其中k的尺寸为：m0×
n0；
[0014]
(2)利用randperm函数构造一个1至n0的随机排列
[0015]
a(i
′
,:)＝randperm(n0)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0016]
其中i
′
＝1,2，
…
,l+3；
[0017]
(3)得到秘钥key＝bin2dec(b)，其中b(i
′
,j
′
)＝k(a(i
′
,j
′
))，j
′
＝1,2，
…
,n0；
[0018]
(4)通过公式(2)对4个子秘钥：x0(i)、系数ε、ε1、θn的初值θ0进行赋值；
[0019]
s3：将图像进行加密处理，包括dna链的交换和dna链的扩散；
[0020]
s4：对图像进行解密处理。
[0021]
上述技术方案有益效果在于：
[0022]
(1)本方案中dna链交换不仅可以改变像素的位置，也可以改变像素值，并且本方案中的dna链的扩散是一种条件性扩散，条件性扩散在加密过程中容易执行，但条件性扩散的消除过程是困难的，因此本发明的加密方法能更好的确保图像的信息安全；
[0023]
(2)本发明的加密算法可以使密文图像的像素值分布具有良好的均衡性和随机性，并能完全隐藏明文图像的有用信息，可以有效防止攻击者的像素值统计性攻击。
附图说明
[0024]
图1为本发明dna链交换过程示意图；
[0025]
图2为本发明dna链扩散过程示意图；
[0026]
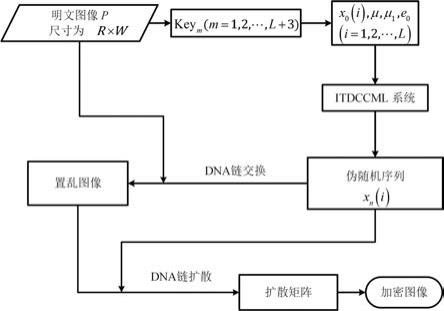
图3为本发明的加密流程框图；
[0027]
图4为本发明中明文图像和加密图像示意图；
[0028]
图5为本发明明文图像和密文图像像素值分布直方图；
[0029]
图6为本发明明文图像与密文图像相邻像素相关性示意图。
具体实施方式
[0030]
本发明的实施是在以本发明技术方案为前提下进行实施的，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述实施例。
[0031]
本发明的具体实施过程如下：
[0032]
一、改进的动态帐篷耦合映射格子的构造
[0033]
根据公式(1-1)所示的动态帐篷耦合映射格子(tdccml系统)，构造如公式(1)所示的改进的动态帐篷耦合映射格子(itdccml系统)
[0034][0035]
其中
[0036][0037]
f(χn(k))＝εχn(k)(1-χn(k))，ε1∈[2,4]，θn表示耦合系数。
[0038][0039]
二、秘钥生成
[0040]
步骤1：利用明文像素值p(i,j)，得到以二进制数k
[0041][0042]
其中k的尺寸为：m0×
n0。
[0043]
步骤2：利用randperm函数构造一个1至n0的随机排列
[0044]
a(i
′
,:)＝randperm(n0)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0045]
其中i
′
＝1,2，
…
,l+3。
[0046]
步骤3：得到秘钥key＝bin2dec(b)，其中b(i
′
,j
′
)＝k(a(i
′
,j
′
))，j
′
＝1,2，
…
,n0。
[0047]
步骤4：按方程(2)对4个子秘钥x0(i)、系数ε、ε1、θn的初值θ0。
[0048][0049]
三、图像进行加密处理
[0050]
(1)dna链的交换
[0051]
步骤1：将明文图像p转化成十进制的矩阵，再将该矩阵转化成二进制形式。采取如表1所示的dna编码第一规则，将二进制矩阵进行dna加密，得到矩阵pd，并按如下形式对pd进行重造：
[0052]
pd←
reshape(pd,2,r
×
w/2)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0053]
规则1234567800aattggcc01gcgcatat10cgcgtata11ttaaccgg
[0054]
表1
[0055]
步骤2：将itdccml系统迭代次，其中表示向上取整，s1表示舍弃前s1次迭代，从s1+1次迭代开始取为混沌序列，而后按如下形式重构x，得到x
[0056][0057]
步骤3：取x的前r
×
w/2项作为一个新的混的序列x
′
，并按方程(6)对x
′
排序
[0058]
[v，σ]＝sort(x
′
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0059]
其中υ是排序向量，σ是x
′
中υ各项对应的索引。
[0060]
步骤4：矩阵pd中每一个元素都由4个碱基构成，可看做一个dna短链。由于pd的尺寸为矩阵pd可视作两组dna短链，第一组短链用pd(1,：)表示，第二组短链用pd(2,：)表示。
[0061]
步骤5：设置两个中间变量：medium1和medium2用于dna链的交换，其中r
×
w/2。
[0062]
步骤6：按方程(7)实现中间变量的交换：
[0063][0064]
其中v＝mod(10*x
′
,4)+1。
[0065]
步骤7：按方程(8)进行dna短链交换：
[0066][0067]
(2)dna链的扩散
[0068]
步骤1：按方程(9)重构矩阵pd用于产生一个dna长链e
[0069]
e＝reshape(pd,1,r
×
w)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0070]
步骤2：将将itdccml系统迭代次，舍弃前s1次迭代，得到一个尺寸为的二维矩阵再按方程(10)重构
[0071][0072]
步骤3：取的前4
×r×
w项作为一个新的混沌序列q
′
，并将q
′
转化为二进制，用第一dna编码规则进行dna加密，得到矩阵q作为另一条dna长链。
[0073]
步骤4：按如下方法进行dna链扩散：
[0074]
当i＝1时，有
[0075][0076]
当1＜i＜r*w/2时，并满足e(8*i-8+j)+
dna
q(8*i-8+j)＝t且e(8*i-7+j)+
dna
q(8*i-7+j)＝＝t，则得到：
[0077][0078]
否则得到：
[0079]
c(8*i-8+j)＝e(8*i-8+j)+
dna
q(8*i-8+j)+
dna
c(8*(i-1)-8+j)；
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0080]
当i＝r*w/2时，得
[0081][0082]
其中和+
dna
分别表示dna异或和dna加法运算，如下表3、表2所示；
[0083]
dna加法agctaagctggctacctagttagc
[0084]
表2
[0085]
dna异或运算agctaagctggatccctagttcga
[0086]
表3
[0087]
四、图像解密
[0088]
步骤1：按如下方法消除dna链扩散效应：
[0089]
当i＝r*w/2时，有
[0090][0091]
当1＜i＜r*w/2时，并满足e(i*8-8+j)＝＝t且e(i*8-7+j)＝＝t，其中则得到：
[0092][0093]
否则得到：
[0094]
e(8*i-8+j)＝c(8*i-8+j)-dna
c(8*(i-1)-8+j)-dna
q(8*i-8+j)；
ꢀꢀꢀ
(17)
[0095]
当i＝1时，得
[0096][0097]
其中-dna
表示dna减法运算，如下表4所示：
[0098]
dna减法运算agct
aatcgggatcccgatttcga
[0099]
表4
[0100]
步骤2：对矩阵e重构，得到二维矩阵pd。
[0101]
步骤3：设置两个中间变量：medium1和medium2用于去除dna链的交换效应，其中用于去除dna链的交换效应，其中
[0102]
步骤4：按方程(19)实现中间变量的交换：
[0103][0104]
其中
[0105]
步骤5：按方程(20)消除dna短链交换效应：
[0106][0107]
步骤6：利用dna第一规则对pd进行dna解密，可得到明文图像。
[0108]
附图4(a)、4(b)分别为lena的明文图像和加密图像，图5(a)、5(b)分别为明文图像和密文图像的像素值分布直方图，从附图4中可以看出，明文图像直方图呈现某种特征，而加密以后的密文图像的直方图呈现平坦而均匀的分布情况，说明本发明的加密算法可以使密文图像的像素值分布具有良好的均衡性和随机性，并能完全隐藏明文图像的有用信息，可以有效防止攻击者的像素值统计性攻击；
[0109]
图6(a)、6(b)分别展示了明文图像和加密图像在水平方向、垂直方向以及对角方向上的相邻像素间的相关性，从中可以看出，明文图像的相邻像素点对集中在对角线上，而密文图像的相邻像素点均匀分布在矩形区域内，这说明明文图像在各个方向上具有较强的相关性，而密文图像则不具有各个方向的相关性，从而更好的确保图像的信息安全。
[0110]
上面所述只是为了说明本发明，应该理解为本发明并不局限于以上实施例，符合本发明思想的各种变通形式均在本发明的保护范围之内。