一种计算机网络集群系统故障的可诊断性确定方法

1.本发明涉及网络故障诊断方法，尤其涉及一种计算机网络集群系统故障的可诊断性确定方法。


背景技术：

2.在计算机网络集群系统中，通常会使用匿名协议保护网络中用户的身份信息。一般来说，发起者发送一条消息给网络服务器，但不能暴露自己是消息来源，所以发起则通常通过大量用户或者自己来发送此消息。当集群中的用户接受消息时，它会发送消息给网络服务器，或者转发此消息给其他用户或自己。因此，网络服务器就不能识别发起者的身份。但系统中可能存在一些泄露消息来源的破坏用户，将转发消息给破坏用户视作为一个故障。因此，需要知道此消息有没有被转发给了破坏用户，以便采取补救措施，也就是故障诊断。
3.计算机网络集群系统等离散事件系统通常可以用peri网和有限自动机来描述，后者比较常见。故障诊断一般有三种形式：集中式故障诊断、分散式故障诊断和分布式故障诊断。集中式故障诊断有且只有一个观测点，而分散式故障诊断有多个观测点，但观测点间没有信息交互。若观测点间存在信息交互，则称为分布式故障诊断。1995年，集中式故障诊断的概念首次提出，并且构造故障观测器给出了故障可诊断的判别条件，但存在指数型的计算复杂度。随后，多个观测点的故障诊断方式首次被提出，许多学者提出了分散式故障诊断和分布式故障诊断的判据。
4.但大部分关于故障诊断的结果都是基于可观事件集是固定的情况下得到的，也就是说可观事件的每次出现都能够被观测到，这种情况下，称为静态事件观测。在实际中，每个可观测事件都有一个传感器，当可观事件出现时，传感器就会把信息通过信道传给观测点，但让传感器一直处于工作状态是不太可能的。因此，这意味着可观事件并不会总是被观测到，称为动态事件观测。在静态事件观测下的分布式故障诊断已经被广泛地研究了，而在动态事件观测的情况下的分布式故障诊断还没有学者进行研究。事实上，静态事件观测下的故障诊断只是动态事件观测下的一种特殊情况。静态事件观测下故障可诊断并不意味着在动态观测下故障可诊断，而若后者成立则一定能够得到静态事件观测下的可诊断的结论。因此，在动态事件观测下去研究分布式故障可诊断更有意义和更具挑战性。


技术实现要素：

5.发明目的：针对现有技术的缺陷，本发明提供一种可以在动态事件观测下确定计算机网络集群系统故障可诊断性的方法。
6.技术方案：本发明所述的计算机网络集群系统故障的可诊断性确定方法包括：
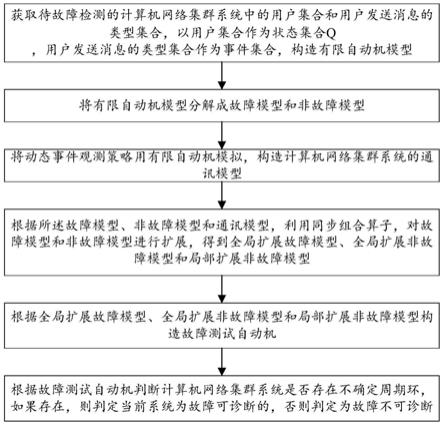
7.(1)获取待故障检测的计算机网络集群系统中的用户集合和用户发送消息的类型集合，以用户集合作为状态集合q，用户发送消息的类型集合作为事件集合σ，构造有限自动机模型g＝(q,σ,δ,q0)，其中，δ表示状态的转移函数，q0代表初始状态；
8.(2)将有限自动机模型g分解成故障模型gf和非故障模型gn；
9.(3)将动态事件观测策略用有限自动机模拟，构造计算机网络集群系统的通讯模型；
10.(4)根据所述故障模型、非故障模型和通讯模型，利用同步组合算子，对故障模型和非故障模型进行扩展，得到全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型：
11.(5)根据全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型构造故障测试自动机；
12.(6)根据故障测试自动机判断计算机网络集群系统是否存在不确定周期环，如果存在，则判定当前系统为故障可诊断的，否则判定为故障不可诊断。
13.进一步的，步骤(2)中所述故障模型gf和非故障模型gn采用下式分解：
14.gn＝g
×an
15.gf＝coac(g
×af
)
16.式中，an表示只有一个状态n的有限自动机，状态n为σ\σf中的任意事件在该状态上形成自环的状态，
×
表示完全同步组合算子，表示完全同步组合算子，表示具有相同故障类型fi的集合，l表示故障类型的数量，coac(g
×af
)表示删除g
×af
中不可能到达故障状态的所有状态所剩下的部分，af＝(qs,σ,δf,q
0,f
)为故障有限自动机，qs＝{n,f}，f表示消息外泄的用户，q
0,f
＝{n}表示af初始状态，δf表示af状态转移函数，δf和f满足以下条件：对任意对任意的η∈∑/∑f,δf(n,η)＝n，且对任意的θ∈σ,δf(f,θ)＝f，形如δf(*,#)表示状态*通过事件#所到达的状态。
17.进一步的，步骤(3)中计算机网络集群系统的通讯模型c
ij
(g)的构造方法为：
18.(3-1)获取每个观测站点的可观事件集∑
oi
和不可观事件集∑
ui
＝∑/∑
oi
，获取动态事件观测策略ωi＝(ri,θi)，其中，i＝1,2,...,nd，nd表示观测站点的数目，是一个确定的自动机，分别表示ri的状态集合、转移函数、初始状态，表示确定可观事件集的映射；
19.(3-2)令集合y＝y0，集合对事件集合∑进行遍历，若其中任意事件σ在由轨迹s所确定的可观事件集合中，则对σ加一个下标i，形成σi加入集合∑i＝{σi}中，s为∑
*
中元素，∑
*
表示由集合中的所有事件组成的有限长度轨迹的集合，ε表示空事件，i＝1,2,...,nd；(3-3)从y中获取任意元素y，并记为对于所有y进行如下处理：如果存在δ(q1,σ)，则令f
yz
(y,σ)＝(y,σ)，并且令z＝z∪f
yz
(y,σ)，其中δ(q1,σ)表示状态q1通过事件σ所到达的状态，σ表示属于事件集合∑中的任意事件；
20.(3-4)从z中获取任意元素z，并记为对于所有z进行如下处理：令变量q3＝δ(q2,σ)，如果那么将加入f
zy
(z,σi)，并且令如果则令加入f
zy
(z,εi)并且令
其中表示由状态所确定的可观事件集合，表示在动态事件观测策略状态集ri中，状态通过事件σ所到达的状态，f
zy
(z,σi)表示状态z∈z到状态y∈y的转移函数，εi表示空事件；
21.(3-5)构造观测站点传递给观测站点消息的通讯模型为
22.进一步的，步骤(4)中扩展的方法具体为：
23.全局扩展故障模型为
24.全局扩展非故障模型为
25.局部扩展非故障模型为
26.其中，||表示同步组合算子，其计算通式为g
*
||g
#
＝ac(q
*
×q#
,σ
*
∪σ
#
,v
*#
,(q
0,*
,q
0,#
))，式中，自动机g
*
＝(q
*
,σ
*
,v
*
,q
0,*
)，q
*
,σ
*
,v
*
,q
0,*
分别为自动机g
*
的状态集合、事件集合、转移函数、初始状态，自动机g
#
＝(q
#
,σ
#
,v
#
,q
0,#
)，q
#
,σ
#
,v
#
,q
0,#
分别为自动机g
#
的状态集合、事件集合、转移函数、初始状态，ac()表示取初始状态可达到的全部状态及其事件轨迹，v
*o
的计算公式为：对任意q
*
,q
#
分别表示自动机g
*
、自动机g
#
中的任意状态；c
ij
(gf)表示基于故障模型gf和由观测站点传递给站点的信息所构造的通讯模型；c
ij
(gn)表示基于非故障模型gn和由观测站点传递给站点的信息所构造的通讯模型；c
ji
(gn)表示基于非故障模型gn和由观测站点传递给站点的信息所构造的通讯模型；
27.进一步的，步骤(5)中构造故障测试自动机的方法具体为：
28.(5-1)对全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型按照一维数字重新标号，编号时保持n和f不变，标号后的模型分别记为和i＝1,2,...,nd，nd表示观测站点的数目，形如q
*
,σ
*
,δ
*
,q
0,*
分别为自动机*的状态集合、事件集合、转移函数、初始状态；
29.(5-2)根据和构造故障测试自动机
[0030][0031]
其中，其中，
[0032][0033]
该故障测试自动机中的状态能够被更新当且仅当满足如下条件：
[0034][0035]
其中，将中第1个状态记为中第1个状态记为为t1中分量，将中第1个元素记为σ
1,0
、σ
1,i
为中分量，的计算通式为：表示状态#根据动态事件观测策略ωi所确定的可观事件集合，映射定义为：对任意的θj∈∑j，γj(θj)＝θ，否则γj(εj)＝ε，θ为中任意元素；
[0036]
当条件被满足时，故障测试自动机的状态t1中的每一个分量根据如下规则更新：
[0037]
如果那么状态t1中的分量更新为更新为不变；
[0038]
如果那么状态t1中的分量更新为更新为更新为
[0039]
如果那么状态t1中的分量更新为更新为
[0040]
如果那么状态t1中的分量更新为更新为不变。
[0041]
进一步的，不确定周期环的判定方法具体为：
[0042]
(6-1)按照下面方法判断故障测试自动机是否存在周期环：
[0043]
如故障测试自动机中存在一条路径满足t
τ+1
＝tk，则该路径被称之为周期环，其中，τ是一个比k大的正整数，t
*
表示故障测试自动机τ的第*个状态，且是中第*个元素,且
[0044]
(6-2)判断周期环是否满足下面条件，满足则判定为不确定周期环：
[0045]
周期环中存在某个状态t
λ
的第一个分量为故障状态，且所对应的事件不为空事件。
[0046]
有益效果：本发明与现有技术相比，其显著优点是：本发明可以在动态事件观测下
确定计算机网络集群系统故障的可诊断性，且效率高。
附图说明
[0047]
图1为本发明流程示意图；
[0048]
图2计算机网络集群系统图；
[0049]
图3计算机网络集群系统所对应的自动机g模型示意图；
[0050]
图4计算机集群系统(图3)中两个地方站点的动态观测模型示意图；
[0051]
图5为计算机集群系统(图3)所对应的故障模型和非故障模型示意图；
[0052]
图6为计算机集群系统(图3)的通讯模型示意图；
[0053]
图7为计算机集群系统(图3)所对应的全局扩展故障模型示意图；
[0054]
图8为计算机集群系统(图3)所对应的局部扩展非故障模型和的示意图；
[0055]
图9为计算机集群系统(图3)故障测试自动机的部分示意图。
具体实施方式
[0056]
本实施例提供了一种计算机网络集群系统故障的可诊断性确定方法，如图1所示，包括如下步骤：
[0057]
(1)获取待故障检测的计算机网络集群系统中的用户集合和用户发送消息的类型集合，以用户集合作为状态集合q，用户发送消息的类型集合作为事件集合σ，构造有限自动机模型g＝(q,σ,δ,q0)，其中，δ表示状态的转移函数，q0代表初始状态。
[0058]
本实施例的计算机集群系统如图2所示，图2中包含两个用户的计算机网络集群系统，发起者为{0}，破坏用户为{6}。用户组1为{0，1，2，3}，用户组2为{4，5，6}。实际上，有两个观测站点观测，图2所对应的有限自动机模型为图3，其中图3只考虑一种故障模型，即l＝1。表1为系统中计算机集群的事件含义表。
[0059]
表1
[0060][0061]
网络管理者可以对集群系统的所有用户操作日志设置权限，假设用户组1和2可以相互可以看到对方的用户操作日志，因此可以视系统为一个分布式系统，对系统的用户操作日志的观测可以看作为两个地方站点的动态观测ω1和ω2。图4为计算机集群系统(图3)中两个地方站点的动态观测ω1和ω2。故障诊断的实质就是若对任意带有故障事件的轨迹，在有限观测长度内，其所对应的观测轨迹与任何不带故障事件轨迹的观测不同，则称为改故障可以被诊断。
[0062]
(2)将有限自动机模型g分解成故障模型gf和非故障模型gn。
[0063]
其中，故障模型gf和非故障模型gn采用下式分解得到：
[0064]gn
＝g
×an
[0065]
gf＝coac(g
×af
)
[0066]
式中，an表示只有一个状态n的有限自动机，状态n为σ\σf中的任意事件在该状态上形成自环的状态，
×
表示完全同步组合算子，表示完全同步组合算子，表示具有相同故障类型fi的集合，l表示故障类型的数量，coac(g
×af
)表示删除g
×af
中不可能到达故障状态的所有状态所剩下的部分，af＝(qs,σ,δf,q
0,f
)为故障有限自动机，qs＝{n,f}，f表示消息外泄的用户，q
0,f
＝{n}表示af初始状态，δf表示af状态转移函数，δf和f满足以下条件：对任意对任意的η∈∑/∑f,δf(n,η)＝n，且对任意的θ∈∑,δf(f,θ)＝f，形如δf(*,#)表示表示状态*通过事件#所到达的状态。图5为计算机集群系统(图3)所对应的故障模型和非故障模型。
[0067]
(3)将动态事件观测策略用有限自动机模拟，构造计算机网络集群系统的通讯模型。
[0068]
其中，计算机网络集群系统的通讯模型c
ij
(g)的构造方法为：
[0069]
(3-1)获取每个观测站点的可观事件集∑
oi
和不可观事件集∑
ui
＝∑/∑
oi
，获取动态事件观测策略ωi＝(ri,θi)，其中，i＝1,2,...,nd，nd表示观测站点的数目，是一个确定的自动机，分别表示ri的状态集合、转移函数、初始状态，表示确定可观事件集的映射；
[0070]
(3-2)令集合y＝y0，集合对事件集合σ进行遍历，若其中任意事件σ在由轨迹s所确定的可观事件集合中，则对σ加一个下标i，形成σi加入集合σi＝{σi}中，s为σ
*
中元素，σ
*
表示由集合中的所有事件组成的有限长度轨迹的集合，ε表示空事件，i＝1,2,...,nd；(3-3)从y中获取任意元素y，并记为，对于所有y进行如下处理：如果存在δ(q1,σ)，则令f
yz
(y,σ)＝(y,σ)，并且令z＝z∪f
yz
(y,σ)，其中δ(q1,σ)表示状态q1通过事件σ所到达的状态，σ表示属于事件集合σ中的任意事件；
[0071]
(3-4)从z中获取任意元素z，并记为，对于所有z进行如下处理：令变量q3＝δ(q2,σ)，如果，那么将加入f
zy
(z,σi)，并且令；如果，则令加入f
zy
(z,εi)并且令其中表示由状态所确定的可观事件集合，表示在动态事件观测策略状态集ri中，状态通过事件σ所到达的状态，f
zy
(z,σi)表示状态z∈z到状态y∈y的转移函数，εi表示空事件；
[0072]
(3-5)构造观测站点传递给观测站点消息的通讯模型为图7为计算机集群系统(图3)的通讯模型c
12
(g)、c
21
(g)。
[0073]
此外，为了更好计算，可以将模型c
ij
(g)用数字0，1，2,
…
进行重新编号后再执行下
面计算。
[0074]
(4)根据所述故障模型、非故障模型和通讯模型，利用同步组合算子，对故障模型和非故障模型进行扩展，得到全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型。
[0075]
其中，扩展的方法具体为：
[0076]
全局扩展故障模型为
[0077]
全局扩展非故障模型为
[0078]
局部扩展非故障模型为
[0079]
式中，||表示同步组合算子，其计算通式为g
*
||g
#
＝ac(q
*
×q#
,σ
*
∪σ
#
,v
*#
,(q
0,*
,q
0,#
))，式中，自动机g
*
＝(q
*
,σ
*
,v
*
,q
0,*
)，q
*
,σ
*
,v
*
,q
0,*
分别为自动机g
*
的状态集合、事件集合、转移函数、初始状态，自动机g
#
＝(q
#
,σ
#
,v
#
,q
0,#
)，q
#
,σ
#
,v
#
,q
0,#
分别为自动机g
#
的状态集合、事件集合、转移函数、初始状态，ac()表示取初始状态可达到的全部状态及其事件轨迹，的计算公式为：对任意
[0080]q*
,q
#
分别表示自动机g
*
、自动机g
#
中的任意状态；c
ij
(gf)表示基于故障模型gf和由观测站点传递给站点的信息所构造的通讯模型；c
ij
(gn)表示基于非故障模型gn和由观测站点传递给站点的信息所构造的通讯模型；c
ji
(gn)表示基于非故障模型gn和由观测站点传递给站点的信息所构造的通讯模型。
[0081]
本实施例中，对于图3所示计算机集群系统扩展的全局扩展故障模型如图7所示，局部扩展非故障模型和如图8所示。
[0082]
(5)根据全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型构造故障测试自动机。
[0083]
构造故障测试自动机的方法具体为：
[0084]
(5-1)对全局扩展故障模型、全局扩展非故障模型和局部扩展非故障模型按照一维数字重新标号，编号时保持n和f不变，标号后的模型分别记为和i＝1,2,...,nd，nd表示观测站点的数目，形如q
*
,σ
*
,δ
*
,q
0,*
分别为自动机*的状态集合、事件集合、转移函数、初始状态；
[0085]
(5-2)根据和构造故障测试自动机
[0086][0087]
其中，
[0088][0089]
该故障测试自动机中的状态能够被更新当且仅当满足如下条件：
[0090][0091]
其中，将中第1个状态记为为t1中分量，将中第1个元素记为σ
1,0
、σ
1,i
为中分量，的计算通式为：表示状态#根据动态事件观测策略ωi所确定的可观事件集合，映射定义为：对任意的θj∈∑j，γj(θj)＝θ，否则γj(εj)＝ε，θ为中任意元素；
[0092]
当条件被满足时，故障测试自动机的状态t1中的每一个分量根据如下规则更新：
[0093]
如果那么状态t1中的分量更新为更新为不变；
[0094]
如果那么状态t1中的分量更新为更新为更新为
[0095]
如果那么状态t1中的分量更新为更新为更新为
[0096]
如果那么状态t1中的分量更新为更新为不变。
[0097]
(6)根据故障测试自动机判断计算机网络集群系统是否存在不确定周期环，如果存在，则判定当前系统为故障可诊断的，否则判定为故障不可诊断。
[0098]
其中，不确定周期环的判定方法具体为：
[0099]
(6-1)按照下面方法判断故障测试自动机是否存在周期环：
[0100]
如故障测试自动机中存在一条路径0≤k≤τ，满足t
τ+1
＝tk，则该路径被称之为周期环，其中，τ是一个比k大的正整数，t
*
表示故障测试自动机的第*个状态，且
是中第*个元素,且
[0101]
(6-2)判断周期环是否满足下面条件，满足则判定为不确定周期环：
[0102]
周期环中存在某个状态t
λ
的第一个分量为故障状态，且所对应的事件不为空事件。
[0103]
图9为计算机集群系统(图3)自动机的一部分。可以从图中发现，自动机含有不确定周期环，因此计算机集群系统(图3)是故障不可诊断的。
[0104]
以上所揭露的仅为本发明一种较佳实施例而已，不能以此来限定本发明之权利范围，因此依本发明权利要求所作的等同变化，仍属本发明所涵盖的范围。