基于遗传算法的不确定参数聚焦匹配场声源功率估计方法

1.本发明属于声源功率估计，涉及一种基于遗传算法的不确定参数聚焦匹配场声源功率估计方法。


背景技术：

2.匹配场声源功率估计方法(matched field source power estimation method:mfpe)根据声传播模型描述浅海波导环境，借助定位方法估计声源位置，使用环境参数和声源位置参数估计信道传递函数，利用了声源辐射的所有能量，得到了最客观真实的声源辐射功率(xiang l f,sun c.an estimation method of ship radiated noise level based on matched field processing.acta acustica,2014；39(5):570-576.)。然而，mfpe要求环境参数和声源位置参数精确已知，当环境参数失配时，信道传递函数估计结果存在偏差，导致声源功率估计结果误差较大。
3.提高mfpe环境失配稳健性的方法尚未提出，提高匹配场定位环境失配稳健性的常用方法有：1)扇区聚焦方法，通过提取接收数据互谱密度矩阵中的主特征值构造投影矩阵，去除互谱密度矩阵中对环境失配较为敏感的部分，从而提高定位结果的稳健性，但无法确保信号能量没有损失；2)minimax方法，环境失配的影响，均表现为信道传递函数的变化，minimax方法利用信道传递函数的夹角和幅度变化范围上下界信息，重构信道传递函数，以提升环境失配稳健性。但该方法的环境失配稳健性提升表现为环境失配时的最差定位性能最优，无法确保最优定位结果的稳健性。
4.在不损失信号能量的需求框架下，信道传递函数的优化是提升环境失配稳健性的关键，在已有先验信息下寻求偏差较小的信道传递函数本质上是一个优化问题。事实上，仅使用声源位置参数变化范围这一先验信息优化信道传递函数，其环境失配稳健性的提升是有限的，原因在于忽略了环境参数不确定性。collins等人引入环境参数变化范围这一先验信息，提出环境聚焦定位方法。该方法扩充搜索空间，在声源位置变化范围和不确定环境参数变化范围内搜索偏差较小的信道传递函数，从而提升定位方法的环境失配稳健性。但该方法现仅用于声源定位，尚未用于解决声源功率估计问题。由于不确定环境参数通常较多，待搜索的不确定参数实现个数呈指数增长，可结合遗传算法等全局优化算法解决。


技术实现要素：

5.要解决的技术问题
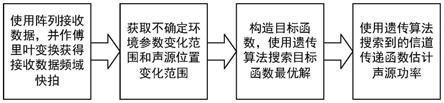
6.为了避免现有技术的不足之处，本发明提出一种基于遗传算法的不确定参数聚焦匹配场声源功率估计方法(uncertain parameters focalization matched field source power estimation method,fmfpe)。方法利用声源位置变化范围和不确定环境参数变化范围获得信道传递函数搜索范围，构造目标函数为估计信道传递函数和接收数据频域快拍的夹角余弦值，结合遗传算法(genetic algorithm,ga)完成信道传递函数的寻优过程，并使用获得的信道传递函数估计值得到环境失配稳健性较高的声源功率估计值。
7.技术方案
8.一种基于遗传算法的不确定参数聚焦匹配场声源功率估计方法，其特征在于步骤如下：
9.步骤1：对均匀垂直线列阵采集信号进行fft处理，得到接收信号频域模型：
10.x＝ha+n
11.式中，x为接收信号频域快拍，h为理想信道传递函数，n为环境噪声，噪声功率为
12.步骤2：构造目标函数
13.其中：hi为第i个网格点对应的备选信道传递函数；
14.步骤3、采用遗传算法进行搜素目标函数的最大值η
ga
：
15.具体搜索过程如下：
16.第一步：初始化，包括设置交叉概率pc和变异概率pm，产生初代种群和设置循环终止条件；
17.交叉概率pc选取范围为0.40～0.99；变异概率pm选取范围为0.001～0.1；
18.初始化种群：采用二进制编码对不确定参数变化范围划分网格；每个不确定参数由k位二进制数表示，则每个不确定参数变化范围均被划分成2
k-1个网格，二进制数与不确定参数值q的对应关系为：
[0019][0020]
式中，lb为不确定参数变化范围的下界，ub为不确定参数变化范围的上界，u为二进制数对应的十进制数；考虑j个不确定参数，则共有2
kj
个网格点，每个网格点对应的不确定参数组用j
×
k位二进制数表示；随机选取pop个网格点，对应pop组不确定参数，将一组不确定参数代入声场软件得到的备选信道传递函数hi即为一个“个体”，pop个个体构成初始种群；
[0021]
设置循环终止条件：设置遗传代数计数器n＝0，选择确定的遗传世代数gen作为迭代终止条件，遗传算法搜索过程需要计算的网格点个数为：
[0022]
num＝pop
×
gen
[0023]
第二步：个体评价，遗传算法的个体适应度由目标函数计算得到；
[0024]
第三步：种群进化
[0025]
选择过程：采用轮盘赌和精英选择两种方法完成“优胜劣汰”的选择过程；
[0026]
交叉过程：将选择过程得到的“子代”个体随机分配，每两个个体分为一组，依次对每一组个体执行如下判断：在0～1范围内产生一个随机数ε1，若ε1＜pc，则对该组个体执行交叉操作，否则不对该组个体执行交叉操作；交叉过程采用单点交叉，在区间[1,j
×
k)内随机产生一点作为交叉点，交叉点将每个个体的二进制串分为两段，将其中一段二进制串交
换生成新的二进制串，交叉过程完成；
[0027]
变异过程：依次对每一个个体执行如下判断：在0～1范围内产生一个随机数ε2，若ε2＜pm，则对该个体执行变异操作，否则不对该个体执行变异操作；变异过程采用单点变异，在区间[1,j
×
k]内随机产生一点作为变异点，将变异点的二进制数反转完成变异过程；
[0028]
第四步：循环终止判断，当n＞gen时终止迭代，输出迭代终止时适应度最大的个体；否则，令n＝n+1，并返回第二步；
[0029]
取信道传递函数理想值h与接收信号频域快拍的夹角余弦值的绝对值作为参考值进行对比，参考值ref的表达式为：
[0030][0031]
经过多次迭代，遗传算法的适应度最大值并接近参考值ref；
[0032]
将遗传算法终止迭代时适应度最大的个体对应的信道传递函数记为η
ga
；
[0033]
步骤4：fmfpe方法得到的声源功率估计值为：
[0034][0035]
所述轮盘赌选择即为从“父代”个体中随机选择pop个个体。
[0036]
所述精英选择即为“父代”的最优个体直接保留下来，轮盘赌选择只产生pop-1个“子代”个体。
[0037]
有益效果
[0038]
本发明提出的一种基于遗传算法的不确定参数聚焦匹配场声源功率估计方法，将扫描范围扩展到包含环境参数和声源位置在内的所有不确定参数，使用备选信道传递函数和接收信号频域快拍的夹角余弦值作为目标函数，结合遗传算法对目标函数寻优，使用遗传算法输出的信道传递函数估计声源功率。fmfpe方法可以减小信道传递函数估计值与理想值的夹角，增强信道传递函数估计值与理想值的相关性，从而提升声源功率估计方法的环境失配稳健性。
[0039]
在本发明中：提出fmfpe方法。扩展搜索范围，利用声源位置变化范围和不确定环境参数变化范围获得信道传递函数搜索范围，并以此作为信道传递函数估计问题的搜索域。构造目标函数为估计信道传递函数和接收数据频域快拍的夹角余弦值，结合遗传算法完成信道传递函数的寻优过程，使用寻优得到的信道传递函数估计声源功率，获得更高的环境失配稳健性。
[0040]
本发明的基本原理和实施方案经过了计算机数值仿真的验证，给出了本发明所提出方法获得的信道传递函数以及遗传算法搜索过程。其结果表明：fmfpe方法有效减小了不同频率的声源功率估计误差；声源在不同位置处时，使用fmfpe方法也可以获得更精确的功率估计结果。通过在不同频率和声源位置条件下估计声源功率，检验了本发明中所提出的fmfpe方法在估计声源功率时的环境失配稳健性。
附图说明
[0041]
图1遗传算法搜索中，单点交叉示意图；
[0042]
图2遗传算法搜索中，单点变异示意图；
[0043]
图3本发明中所涉及步骤的主要流程；
[0044]
图4本发明中利用遗传算法搜索信道传递函数的流程；
[0045]
图5实施实例中，benchmark标准浅海环境声速剖面；
[0046]
图6实施实例中，环境不确定性对信道传递函数模值和夹角的影响。
[0047]
图7实施实例中，遗传算法搜索到的信道传递函数的rom和cosθ随snr的变化。
[0048]
图8实施实例中，snr为10db时，f
ave
和f
max
随遗传世代数的变化。
[0049]
图9实施实例中，snr为30db时，f
ave
和f
max
随遗传世代数的变化。
[0050]
图10实施实例中，不同snr时，fmfpe方法和mfpe方法的声源功率估计结果。
[0051]
图11实施实例中，不同频率时，fmfpe方法和mfpe方法的声源功率估计结果。
[0052]
图12实施实例中，声源在不同深度时，fmfpe方法和mfpe方法的声源功率估计结果。
[0053]
图13实施实例中，声源到接收基阵的距离变化时，fmfpe方法和mfpe方法的声源功率估计结果。
具体实施方式
[0054]
现结合实施例、附图对本发明作进一步描述：
[0055]
本发明解决现存问题所采用的技术方案可分为以下2个步骤：
[0056]
1、对信道传递函数优化问题建模。利用不确定参数变化范围获得信道传递函数搜索范围，并以此作为信道传递函数问题的搜索域；构造用于声源功率估计问题的目标函数即本发明的贡献。
[0057]
2、结合遗传算法求解信道传递函数优化问题，获得信道传递函数估计结果，并使用该信道传递函数估计值得到fmfpe的声源功率估计值即本发明的贡献。
[0058]
步骤1)所涉及的具体内容如下：
[0059]
结合声场模型计算信道传递函数需要使用声源位置参数和环境参数，环境不确定时，使用真实声源位置处的信道传递函数必定存在偏差；使用估计声源位置处的信道传递函数也存在偏差，原因在于，扫描区域仅为声源位置参数变化范围，在失配环境下扫描时，搜索域内不存在真实参数；搜索结果只能获得一系列失配传递函数中偏差较小的信道传递函数。为了进一步降低搜索获得的信道传递函数的偏差，考虑扩展搜索域，在环境参数变化范围和声源位置参数变化范围内同时扫描。此时，搜索域内存在真实参数，但由于搜索精度的限制，搜索结果通常是信道传递函数理论最优解的近似解。
[0060]
假设利用均匀垂直线列阵采集信号，接收信号频域模型可以表示为：
[0061]
x＝ha+n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0062]
式中，x为接收信号频域快拍，h为理想信道传递函数，n为环境噪声，噪声功率为定义阵列接收信噪比(signal to noise ratio:snr)为：
[0063][0064]
为了搜索偏差较小的信道传递函数，首先需要度量信道传递函数的偏差。信道传
递函数是一个向量，向量的偏差可以用模值偏差和夹角描述。信道传递函数估计值用表示，信道传递函数的模值偏差可由和h的模值之比描述：
[0065][0066]
式中，符号
‘
|| ||’表示二范数。信道传递函数之间的夹角可由和h的夹角余弦值表示：
[0067][0068]
观察(3)(4)式不难发现：rom和cosθ只有分母不同，对比分子可知，信道传递函数之间的夹角对环境失配更加敏感；因此，考虑使用夹角余弦值作为优化问题的目标函数。实际上，理想信道传递函数h无法获得。由于(4)式中对和h均作模值归一化处理，cosθ中不包含模值信息；在信噪比较大时，可以使用接收信号频域快拍x代替理想信道传递函数h。
[0069]
通常对参数变化范围划分网格，并依次搜索网格点对应的不确定参数组。信道传递函数与网格点对应的不确定参数组具有一一对应关系，第i个网格点对应的备选信道传递函数记为hi。构造fmfpe方法的目标函数为：
[0070][0071]
(5)式本质上是hi和x的相关系数，在声源位置参数和环境参数变化范围内，使f(hi)最大的参数组对应的信道传递函数即为与理想信道传递函数偏差较小的估计信道传递函数。由于环境噪声的存在且目标函数未考虑模值，搜索结果只能得到与理想信道传递函数的偏差在可接受误差范围内的满意解。
[0072]
步骤2)所涉及的具体内容如下：
[0073]
为了获得更精确的信道传递函数估计值，通常需求网格间距较小；由于不确定参数通常较多，待搜索的网格点个数呈指数增长，遍历搜索的计算量要求过于庞大。fmfpe方法中的信道传递函数估计问题本质上是一个最优化问题，在搜索域与目标函数已知的情况下，可以使用遗传算法等智能全局优化算法完成搜索过程。遗传算法将迭代过程看作遗传进化过程，基本思想是模拟自然界遗传机制和生物进化论。遗传算法迭代的单位为一个
‘
种群’，种群中有多个
‘
个体’，用
‘
基因’表示每个个体对应的不确定参数组，用
‘
适应度’表示个体在种群中的竞争优势；适应度越大，个体的竞争优势越大；适应度通常为最优化问题的目标函数，即由(5)式计算得到。迭代终止时，输出种群中适应度最大的个体对应的不确定参数组和信道传递函数，该信道传递函数与理想信道传递函数的偏差较小，用来估计声源功率可以提高环境失配稳健性。
[0074]
具体搜索过程如下：
[0075]
第一步：初始化，包括设置交叉概率pc和变异概率pm，产生初代种群和设置循环终止条件。
[0076]
设置交叉概率pc和变异概率pm。pc和pm分别影响遗传算法的搜索能力和“跳出”极值点的能力，交叉概率和变异概率普遍的选择标准和推荐范围为，交叉概率pc较大，选取范围为0.40～0.99；变异概率pm较小，选取范围为0.001～0.1。
[0077]
初始化种群。采用二进制编码对不确定参数变化范围划分网格；每个不确定参数由k位二进制数表示，则每个不确定参数变化范围均被划分成2
k-1个网格，二进制数与不确定参数值q的对应关系为：
[0078][0079]
式中，lb为不确定参数变化范围的下界，ub为不确定参数变化范围的上界，u为二进制数对应的十进制数。考虑j个不确定参数，则共有2
kj
个网格点，每个网格点对应的不确定参数组可以用j
×
k位二进制数表示。随机选取pop个网格点，对应pop组不确定参数，将一组不确定参数代入声场软件得到的备选信道传递函数hi即为一个“个体”，pop个个体构成初始种群。
[0080]
设置循环终止条件。设置遗传代数计数器n＝0，一般选择确定的遗传世代数gen作为迭代终止条件，对信道传递函数影响较大的不确定参数个数越多，遗传世代数gen越大。遗传算法搜索过程需要计算的网格点个数为：
[0081]
num＝pop
×
gen
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0082]
对比num和2
kj
可知，遗传算法能显著降低需要搜索的网格点个数，快速收敛到最优解。
[0083]
第二步：个体评价。遗传算法的个体适应度由(5)式计算得到。
[0084]
第三步：种群进化，包括选择，交叉，变异等过程。
[0085]
选择过程。采用轮盘赌和精英选择两种方法完成“优胜劣汰”的选择过程。轮盘赌选择即为从“父代”个体中随机选择pop个个体，根据个体适应度不同，每个个体被选到的概率也不同；个体被选到的概率随个体适应度增大而增大，从而确保适应度高的个体竞争优势更大，实现“优胜劣汰”。由于轮盘赌依概率随机选择个体，虽然适应度最高的个体被选中的概率最大，但仍存在被淘汰的可能。精英选择即为“父代”的最优个体直接保留下来，轮盘赌选择只产生pop-1个“子代”个体，采用精英选择可以避免“父代”的最优个体被淘汰。
[0086]
交叉过程。交叉过程是产生新个体的主要方法。将选择过程得到的“子代”个体随机分配，每两个个体分为一组，依次对每一组个体执行如下判断：在0～1范围内产生一个随机数ε1，若ε1＜pc，则对该组个体执行交叉操作，否则不对该组个体执行交叉操作。交叉过程采用单点交叉，图1给出了单点交叉示意图。在区间[1,j
×
k)内随机产生一点作为交叉点，交叉点将每个个体的二进制串分为两段，将其中一段二进制串交换生成新的二进制串，交叉过程完成。
[0087]
变异过程。变异过程是产生新个体的辅助方法，决定了遗传算法的局部搜索能力。依次对每一个个体执行如下判断：在0～1范围内产生一个随机数ε2，若ε2＜pm，则对该个体执行变异操作，否则不对该个体执行变异操作。变异过程采用单点变异，图2给出了单点变异示意图。在区间[1,j
×
k]内随机产生一点作为变异点，将变异点的二进制数反转完成变异过程。
[0088]
第四步：循环终止判断。当n＞gen时终止迭代，输出迭代终止时适应度最大的个
体；否则，令n＝n+1，并返回第二步。
[0089]
取信道传递函数理想值h与接收信号频域快拍的夹角余弦值的绝对值作为参考值进行对比，参考值ref的表达式为：
[0090][0091]
经过多次迭代，遗传算法的适应度最大值非常接近参考值ref。
[0092]
将遗传算法终止迭代时适应度最大的个体对应的信道传递函数记为η
ga
，在任一频点处，fmfpe方法得到的声源功率估计值为：
[0093][0094]
本发明的主要流程如图3所示，遗传算法的流程如图4所示。
[0095]
实施实例
[0096]
以nrl workshop'93提供的benchmark标准浅海环境声速剖面为例，给出本发明的实施实例。实施实例利用计算机进行数值仿真，声场计算采用基于简正波方法的krakenc声场软件，以此检验本发明所提方法的效果。
[0097]
1)浅海不确定环境参数
[0098]
benchmark标准浅海环境声速剖面如图5所示，不确定环境参数标称值和变化范围已在图中给出，假设不确定环境参数在变化范围内均服从均匀分布。图中黑色实线表示声速剖面标称值，海水中为线性负梯度声速剖面，沉积层中为线性正梯度声速剖面，基底半空间声速与沉积层下表面声速保持一致；左右两边的虚线分别代表声速剖面的下界和上界。基底半空间与沉积层的吸收系数α和密度ρ保持一致，沉积层厚度始终保持不变。研究海域深度为1m～100m，距离为1m～1000m。
[0099]
2)发射和接收换能器参数
[0100]
使用阵元间距为1m的100元均匀垂直线列阵接收数据，其中最靠近海面的阵元深度为1m。fmfpe方法逐一测量不同频点的声源功率，假设在任一频点处的信号功率标称值为100db，被测声源深度标称值为50m，被测声源到接收阵的距离标称值为500m。声源辐射信号多为宽带信号，假设信号频率变化范围为100hz～1000hz，仿真分析采用的蒙特卡洛次数为1000次。
[0101]
3)仿真分析环境不确定性对信道传递函数模值和夹角及声源功率估计性能的影响
[0102]
假设被测声源深度和被测声源到接收阵的距离均取标称值，信号频率为500hz。在不确定环境参数变化范围内随机产生1000组环境参数实现，使用krakenc简正波声场模型得到1000个估计信道传递函数；将环境参数标称值代入简正波声场模型得到理想信道传递函数，根据(3)(4)式得到rom和cosθ，如图6所示。rom和cosθ的理想值都是1，1000次蒙特卡洛仿真结果中，rom的均值为0.9923，方差为0.0029；cosθ的均值为0.5905，方差为0.0764；说明环境失配对rom影响较小，对cosθ影响更大。mfpe方法的声源功率估计结果均值为94.3009db，误差为5.6991db，方差为22.6555，可见环境失配对声源功率估计性能影响很大。
[0103]
4)仿真分析遗传算法的搜索性能
[0104]
考虑的不确定参数共9个，包括7个不确定环境参数和2个声源位置参数，声源位置参数分别为被测声源深度和被测声源到接收基阵的距离。取交叉概率为0.8，变异概率为0.05；9个不确定参数均采用12位二进制数编码，则每个不确定参数均划分了2
12-1＝4095个网格；取个体数pop＝100，世代数gen＝200，则一次遗传算法需要计算100
×
200＝2
×
104个网格点。相同的条件下，采用遍历搜索则需要计算29×
12
≈3.25
×
10
32
个网格点，可见，遗传算法极大的减少了需要搜索的网格点数，降低了计算量。
[0105]
假设信号频率500hz，环境噪声为白噪声，噪声级为52db，图7给出了遗传算法搜索到的信道传递函数的rom和cosθ随snr的变化。当snr＞0db，rom和cosθ逐渐收敛于理想值1，说明遗传算法搜索到的信道传递函数与理想信道传递函数的差异逐渐减小。假设snr为10db，适应度由(5)式计算得到，适应度参考值ref为0.8092。f
ave
和f
max
分别表示适应度均值和适应度最大值，图8给出了f
ave
和f
max
随遗传世代数的变化。在前25世代，f
ave
和f
max
迅速增大；从13到24世代，f
max
为0.696保持不变，说明搜索过程收敛于极值点，并在第25世代跳出极值点；从26到200世代，f
ave
和f
max
逼近ref，迭代结束时输出的适应度最大值为0.7999。假设snr为30db，图9给出了f
ave
和f
max
随遗传世代数的变化。搜索过程在第6世代收敛于极值点，在迭代结束时仍未能跳出极值点，此时，需要加大遗传世代数gen。fmfpe方法使用遗传算法搜索到的信道传递函数估计声源功率，均值为99.7443db，误差为0.2527db，方差为0.2883，可见fmfpe方法的环境失配稳健性很高，声源功率估计误差很小。
[0106]
5)仿真分析fmfpe方法在不同snr条件下的声源功率估计性能
[0107]
假设信号频率为500hz，snr在-20db到30db范围内变化，图10给出了不同snr时，fmfpe方法和mfpe方法的声源功率估计结果。从图中可以看到，声源功率估计误差随snr减小而增大，snr低于5db时，环境噪声为影响声源功率估计性能的主要因素，很难区分不同声源功率估计方法环境失配稳健性的差别；因此，下面仿真分析均在snr较大的条件下进行。snr大于5db时，环境不确定性为影响声源功率估计性能的主要因素。以snr为20db时为例，mfpe方法的声源功率估计值为94.3db，误差可达-5.7db；fmfpe方法的声源功率估计值为99.75db，误差为-0.25db。可见，fmfpe方法的环境失配稳健性显著提升。
[0108]
6)仿真分析fmfpe方法在不同频率条件下的声源功率估计性能
[0109]
实际声源辐射的信号一般为宽带信号，仿真分析不同频率时fmfpe方法的声源功率估计性能。假设snr为20db，频率变化范围为100hz～1000hz，图11给出了不同频率时，fmfpe方法和mfpe方法的声源功率估计结果。在低频段，环境不确定性对mfpe方法的影响较小，频率100hz时的声源功率估计结果为99.49db，误差仅为0.51db；随着频率升高，环境不确定对mfpe方法的影响迅速增大，频率1000hz时的声源功率估计误差约为6.5db。fmfpe方法在100hz～1000hz频率范围内，声源功率估计结果均小于99db，声源功率估计值与标称值的偏差均小于1db；可见，fmfpe方法能在更大的频率范围内获得更精确的的声源功率估计值，在较高频段内，环境失配稳健性的提升尤其明显。
[0110]
7)仿真分析fmfpe方法在不同声源位置条件下的声源功率估计性能
[0111]
被测声源可能在海域内任一位置，仿真分析声源在不同位置时fmfpe方法的声源功率估计性能。假设snr为20db，被测声源深度变化范围为1m～100m，图12给出了声源在不同深度时，fmfpe方法和mfpe方法的声源功率估计结果。环境不确定时，mfpe方法的声源功
率估计结果在95db～97.1db范围内变化，误差最小为2.9db。fmfpe方法的声源功率估计结果在98.7db～100.1db范围内变化最大为1.3db；声源深度在5m～100m范围内，fmfpe方法的声源功率估计结果误差小于0.5db。
[0112]
被测声源到接收基阵的距离的变化范围为1m～1000m，图13给出了声源到接收基阵的距离变化时，fmfpe方法和mfpe方法的声源功率估计结果。环境不确定时，mfpe方法的声源功率估计误差随声源到接收基阵的距离增大迅速增大，声源距离接收基阵1000m时，mfpe方法的声源功率估计结果为95db，误差为5db。声源到接收基阵的距离增大，fmfpe方法的声源功率估计值与标称值的偏差也增大，但速度缓慢；在声源距离接收基阵1000m时，fmfpe方法的声源功率估计结果为99.06db，误差仅为0.94db。可以看出：对不同位置的声源，fmfpe方法可以有效减小声源功率估计结果的误差，提高环境失配稳健性。
[0113]
根据实施实例，可以认为本发明中所提出的基于遗传算法的不确定参数聚焦匹配场声源功率估计方法，通过扩展扫描范围，构造目标函数并在扫描范围内寻优，能有效降低估计信道传递函数与理想信道传递函数的偏差，使用搜索得到的信道传递函数，成功获得高精度的声源功率估计值，有效提高了环境失配稳健性。