不确定度预测方法、装置、电子设备及存储介质与流程

1.本技术属于电力系统运行控制技术领域，具体涉及一种不确定度预测方法、装置、电子设备及存储介质。


背景技术：

2.风机功率曲线显示了发电功率和风速之间的关系，在评估风电场的性能方面起着重要作用。然而，在实际应用中，由于大气变量的随机性质，以及影响风力涡轮机的各种因素，功率曲线估计存在不确定性。
3.不确定性有两种，一种是偶然不确定性(aleatoric uncertainty)，是由于观测数据中的固有噪声导致的，这种不确定性是无法被消除的。另一种是感知不确定性(epistemicuncertainty)，与模型相关，是由于训练不完全导致的。如果给它更多的训练数据来弥补现有模型知识上的不足，这种不确定性从理论上来说是可以消除的。
4.然而，现有的不确定性预测方法存在计算复杂性高和预测精度不高的问题。因此，有必要研究一种简单、精确的风电功率不确定度预测方法。


技术实现要素：

5.本技术旨在至少解决现有技术中存在的技术问题之一，提供一种不确定度预测方法、装置、电子设备及存储介质。
6.本技术的第一方面提供一种不确定度预测方法，包括：
7.获取风电场的实际运行数据；
8.对所述实际运行数据进行预处理；
9.采用蒙特卡罗dropout方法对预处理结果进行预测并输出风电功率的任意不确定度和认知不确定度。
10.可选的，所述对所述实际运行数据进行预处理包括：
11.从所述实际运行数据中提取稳态数据；
12.从所述稳态数据中提取主要预测因子。
13.可选的，所述从所述实际运行数据中提取稳态数据，包括：
14.采用随机采样一致算法筛选实际运行数据中的采样点；
15.对筛选的采样点进行最小二乘拟合得到稳态数据，并以时间序列的形式提供数据的平均值、标准差、最小值和最大值。
16.可选的，所述主要预测因子包括风速、环境温度、风向、叶片俯仰角、机舱角、湍流强度、阵风系数和风速比中的一种或多种。
17.可选的，所述采用蒙特卡罗dropout方法对预处理结果进行预测并输出风电功率的任意不确定度和认知不确定度，包括：
18.以蒙特卡洛dropout方法建立基于贝叶斯的概率神经网络模型；
19.利用训练好的神经网络对预处理结果进行多次前向传播，并以不同网络结构输出
多个预测结果的方差，以确定风电功率的认知不确定度；
20.修正概率神经网络模型的损失函数，以输出方差的形式求解任意不确定度。
21.可选的，所述神经网络包括：
22.多个依次相连的隐藏层，每个所述隐藏层包括多个处理单元，其中一个处理单元用于网络端的平均和统计方差输出；每个所述隐藏层还包括激活函数层；每个所述隐藏层中均放置有dropout。
23.可选的，所述修正概率神经网络模型的损失函数，包括：
24.利用神经网络的损失函数对风电功率的任意不确定度进行建模。
25.本技术的第二方面提供一种不确定度预测装置，包括：
26.获取模块，用于获取风电场的实际运行数据；
27.预处理模块，用于对所述实际运行数据进行预处理；
28.预测模块，用于采用蒙特卡罗dropout方法对预处理结果进行预测并输出风电功率的任意不确定度和认知不确定度。
29.本技术的第三方面提供一种电子设备，包括：
30.一个或多个处理器；
31.存储单元，用于存储一个或多个程序，当所述一个或多个程序被所述一个或多个处理器执行时，能使得所述一个或多个处理器实现本技术第一方面所述的不确定度预测方法。
32.本技术的第四方面提供一种计算机可读存储介质，其上存储有计算机程序，
33.所述计算机程序被处理器执行时能实现本技术第一方面所述的不确定度预测方法。
34.本技术实施例至少可以解决以下问题：
35.本技术实施例的不确定度预测方法，结合了神经网络和贝叶斯概率推理的优点，可以减低计算复杂性，而且，该方法可同时估计风电功率的认知不确定度和任意不确定度，有利于提高预测精度。
附图说明
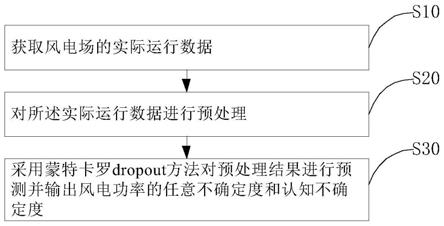
36.图1为本技术一实施例提供的一种不确定度预测方法的流程示意图；
37.图2为本技术一实施例提供的对所述实际运行数据进行预处理的流程示意图；
38.图3为本技术一实施例提供的对预处理结果进行预测的方法的流程示意图；
39.图4为本技术一实施例提供的一种神经网络的结构示意图；
40.图5为本技术一实施例提供的一种不确定度预测装置的结构示意图；
41.图6是本技术一实施例提供的一种电子设备的结构示意图。
具体实施方式
42.为使本领域技术人员更好地理解本技术的技术方案，下面结合附图和具体实施方式对本技术作进一步详细描述。
43.如图1所示，本技术实施例提供了一种不确定度预测方法，包括：
44.s10、获取风电场的实际运行数据。
45.其中，所述实际运行数据包括风速、环境温度、风向、叶片俯仰角、机舱角、湍流强度、阵风系数和风速比等。示例性的，所述实际运行数据可以是中国某地4台风力涡轮机1年的 scada数据。
46.s20、对所述实际运行数据进行预处理，作为神经网络的输入。
47.如图2所示，预处理过程包括：
48.s21、从所述实际运行数据中提取稳态数据。
49.其中，所述从所述实际运行数据中提取稳态数据，包括：
50.采用随机采样一致算法筛选采样点；
51.对筛选的采样点进行最小二乘拟合得到稳态数据，并以时间序列的形式提供数据的平均值、标准差、最小值和最大值。
52.在一些实施例中，所述从所述实际运行数据中提取稳态数据的过程具体可以是：获取风电场数据样本，定义数据总长度为l；根据采样间隔，结合风电机组的运行特性，定义窗口初始长度h，取滑动窗口初始位置h0＝0；判断h+h0是否小于数据总长度l，若h+h0》l，结束该流程，若h+h0《l，取h0+1到h0+h个数据点作为采样点，进行ransac算法筛选；对筛选后的点进行最小二乘拟合，对拟合后的多项式x(i)＝p0+p1i+p2i2+p
mim
进行稳态检测，采用的稳态判别条件为：
53.1)预处理数据最小二乘拟合后曲线模型多项式滤波值的最大与最小值差值小于给定阈值。
54.2)随机采样一致算法筛选出的“内点”的预处理数据的最大与最小值差值小于给定阈值。
55.3)曲线模型p1系数小于给定阈值。
56.若同时满足以上三个条件，则我们认为该窗口的数据为稳态数据。
57.s22、从所述稳态数据中提取主要预测因子。
58.其中，所述主要预测因子包括风速、环境温度、风向、叶片俯仰角、机舱角、湍流强度、阵风系数和风速比等中的一种或多种。
59.在一些实施例中，风速是风力发电的主要预测指标；其他大气变量，如空气温度已被发现对风电功率有贡献；风向在存在偏航偏差时对风电功率有较大贡献；方向角通过正弦函数进行变换，也考虑用作自变量；风电场数据中的涡轮机的机舱角，叶片的俯仰角也会影响功率输出，考虑将这些参数都包括在后续风电功率预测中。其中，湍流强度、阵风系数和风速比需依据实际运行数据计算得到，其余参数可直接得到。
60.湍流强度的增加会导致产生的功率偏离标准曲线，根据公式(1)计算得到；
[0061][0062]
式中，v-表示平均风速，σv表示给定时间间隔内风速的标准偏差。
[0063]
风速比是不同高度风速的比率，计算公式如下：
[0064][0065]
其中v表示高度z处的速度，v0表示高度z0处的速度。
[0066]
阵风系数g是指示给定时间内最大风速v
max
与平均风速v-相比较的指标，
[0067][0068]
例如，神经网络的输入如表1所示。
[0069]
表1数据预处理结果
[0070][0071]
s30、采用蒙特卡罗dropout(monte carlo dropout，mc dropout)方法对预处理结果进行预测并输出风电功率的任意不确定度和认知不确定度。
[0072]
其中，对预处理结果进行预测的具体过程包括：
[0073]
s31、以蒙特卡洛dropout方法建立基于贝叶斯的概率神经网络模型。
[0074]
其中，所述概率神经网络模型包括：
[0075]
多个依次相连的隐藏层，每个所述隐藏层包括多个处理单元，其中一个处理单元用于网络端的平均和统计方差输出；每个所述隐藏层还包括激活函数层；每个所述隐藏层中均放置有dropout。
[0076]
如图4所示，在一些实施例中，所述概率神经网络模型可以将四个完全连接的隐藏层叠加在一起，每个隐藏层由1024个处理单元和两个平行层组成，其中一个处理单元用于网络端的平均和统计方差输出。输入也前馈到所述隐藏层的第一层和第四层。激活函数tanh(
·
) 用于各个隐藏层，线性激活函数用于输出层。根据优化算法设置的伯努利分布概率，将dropout 放置在层之间。
[0077]
s32、利用训练好的神经网络对预处理结果进行多次前向传播，并以不同网络结构输出多个预测结果的方差，以确定风电功率的认知不确定度。
[0078]
其中，所述模型参数的认知不确定度的获取过程包括：
[0079]
s33、修正概率神经网络模型的损失函数，以输出方差的形式求解任意不确定度。
[0080]
其中，所述修正概率神经网络模型的损失函数，包括：
[0081]
利用神经网络的损失函数对风电功率的任意不确定度进行建模。
[0082]
在一些实施例中，利用概率神经网络模型的损失函数对风电功率的任意不确定度进行建模的过程可以是：
[0083]
设概率神经网络模型后验预测函数计算公式如下：
[0084]
p(y
new
|d)＝∫p(y
new
|d,w)p(w|d)dw
ꢀꢀ
(4)
[0085]
其中，y
new
为模型预测值，d＝(x,y)为训练数据集，w为模型参数。
[0086]
为得到上述公式的积分，应具有给定训练数据参数的后验分布。根据贝叶斯定理，可以改写后验分布，便于后续计算，改下如下：
[0087]
[0088]
最小化由潜变量θ参数化的近似分布q
θ(
w)和p(w|d)的实际后验分布之间的散度 (kullback-leibler，kl)，根据kl可得到q
θ
(w)和p(w|x)的近似值：
[0089]
l(θ)＝-∫q
θ
(w)logp(y|x,w)dw+kl(q
θ
(w)||p(w))
ꢀꢀ
(6)
[0090]
式(6)中的积分仍较难解，可采用蒙特卡罗积分作为近似解。
[0091]
在最小化的每个步骤中，从q
θ
(w)中抽取样本来评估网络输出，在训练阶段重复此过程可优化损失函数。
[0092]
假设q
θ
可以分层分解，即:
[0093][0094]
其中，i表示层编号，在每一层，q
θ
被参数化为权重矩阵的平均值乘以对角线矩阵，对角线矩阵由0和1组成，从伯努利分布中采样，概率为pi。故部分权重被随机设置为零。
[0095][0096]
其中，l表示特征长度(超参数)，k表示第i层处理单元的数量，h表示概率为pi的伯努利分布的熵，下标i表示层数。因此，建立了一个由训练样本的对数似然和(8) 的调节项组成的网络损失函数，使q
θ
接近p(w|d)的真实后验概率分布函数。由于(6)的梯度是最小化所需要的，因此需要解决在(8)的熵项中出现的伯努利分布的不连续性问题。为此，采用了伯努利分布的连续近似。这样，通过最小化网络的损失函数，可以找到dropout伯努利分布的最佳概率。
[0097]
在假设噪声服从高斯分布的情况下，可以通过修改损失函数来通过训练过程估计任意不确定性。损失函数可如下表示：
[0098][0099]
其中，下标a表示任意不确定度。(9)的损失函数作为(6)中积分的核。(4)的预测概率可通过w的抽样和网络的前馈预测来近似。前馈预测的平均值：
[0100][0101]
其中，c为前馈评估次数，为模型在第i次评估时输出，x
new
表示训练数据集。相应方差计算如下所示
[0102][0103]
其中，s表示测试数据集，i为模型评估次数w指模型参数；上述方差是认知不确定度的指标，由下标e表示，来源于训练数据集p(w|d)更新的模型参数中的不确定度。
[0104]
选择adam优化算法最小化式(6)中的损失函数，调整其学习率。训练结束后，对与训练集没有重叠的测试集进行估计。为了评估认知不确定度分布，对每个输入样本进行前馈输出评估并记录结果。将平均值作为估计功率值，σe作为认知不确定度。方差的对数由图4的对数(方差)层计算，即ln(σ
a2
)是任意不确定性的度量。
[0105]
认知不确定度体现了模型的质量，包括训练样本的质量以及模型的复杂性，通过
认知不确定度可以用来改变模型的训练过程；由于训练数据中存在噪声干扰，任意不确定度是通过改变训练过程中的损失函数进行估计的，主要起到量化数据中的噪声水平的作用。本技术所提出的不确定度预测方法基于蒙特卡洛dropout方法结合贝叶斯神经网络，可以结合二者优点，避免了复杂的计算，并且dropout可以避免过拟合的影响。
[0106]
由结果可知，模型的认知不确定度容易在风速的上下边界值增加，特别是在上边界。这意味着，由于这些区域的数据点较少，模型估计能力受到限制。此外，数据点比数据集的主体更远，表现出更大的认知不确定度。其次，对于联合输入输出概率较低的样本，其计算的随机不确定度较高。该算法将这些样本作为噪声处理，并将损失函数的标准差调整到较高的值，以减少它们对输出的影响。
[0107]
至此，凭借mc dropout方法得到了认知不确定度，通过修改损失函数得到了任意不确定度。最后，基于4个不同数据集分别建立nn、rf、gb和gpr模型四种功率估计模型，与提出的mc dropout神经网络模型进行比较，并以平均绝对误差作为评价指标，结果如表2所示。结果表明，mc dropout神经网络模型在所有数据集上都优于其他模型。
[0108]
表2四种模型于四个数据集的模型性能
[0109][0110]
这种基于mc dropout的风电功率不确定度预测方法，可同时得到认知不确定度和任意不确定度。该方法结合了神经网络的优势和贝叶斯概率推理的优势，而不受后者令人望而却步的计算复杂性。结果表明mc dropout方法在输出功率的平均绝对误差方面具有更高的精度。
[0111]
贝叶斯神经网络具有良好的应用前景。可将所提出的mc dropout方法用于整个风电场的预测，可求取预测功率的置信区间，从而实现更可靠的规划。除此之外，还可用于评估具有相关不确定度的年度功率预测。该方法对异常点的识别能力可用于风电系统的异常、故障和状态监测。
[0112]
如图5所示，本技术实施例还提供一种不确定度预测装置，包括：
[0113]
获取模块，用于获取风电场的实际运行数据；
[0114]
预处理模块，用于对所述实际运行数据进行预处理，处理结果作为神经网络的输入；
[0115]
预测模块，用于采用蒙特卡罗dropout方法对预处理结果进行预测并输出风电功率的任意不确定度和认知不确定度。
[0116]
本技术实施例所述的不确定度预测装置可以是装置，也可以是终端中的部件、集成电路、或芯片。该装置可以是移动电子设备，也可以为非移动电子设备。示例性的，移动电子设备可以为手机、平板电脑、笔记本电脑、掌上电脑、车载电子设备、可穿戴设备、超级移
动个人计算机(ultra-mobile personal computer，umpc)、上网本或者个人数字助理(personal digitalassistant，pda)等，非移动电子设备可以为服务器、网络附属存储器(network attached storage， nas)、个人计算机(personal computer，pc)、电视机(television，tv)、柜员机或者自助机等，本技术实施例不作具体限定。
[0117]
本技术实施例中的不确定度预测装置可以为具有操作系统的装置。该操作系统可以为安卓 (android)操作系统，可以为ios操作系统，还可以为其他可能的操作系统，本技术实施例不作具体限定。
[0118]
本技术实施例提供的不确定度预测装置能够实现图1至图3的方法实施例实现的各个过程，为避免重复，这里不再赘述。
[0119]
如图6所示，本技术实施例还提供一种电子设备m00，包括处理器m01，存储器m02，存储在存储器m02上并可在所述处理器m01上运行的程序或指令，该程序或指令被处理器 m01执行时实现上述不确定度预测方法实施例的各个过程，且能达到相同的技术效果，为避免重复，这里不再赘述。
[0120]
需要说明的是，本技术实施例中的电子设备包括上述所述的移动电子设备和非移动电子设备。
[0121]
本领域技术人员可以理解，电子设备m00还可以包括给各个部件供电的电源(比如电池)，电源可以通过电源管理系统与处理器m01逻辑相连，从而通过电源管理系统实现管理充电、放电、以及功耗管理等功能。图5中示出的电子设备结构并不构成对电子设备的限定，电子设备可以包括比图示更多或更少的部件，或者组合某些部件，或者不同的部件布置，在此不再赘述。
[0122]
本技术实施例还提供一种可读存储介质，所述可读存储介质上存储有程序或指令，该程序或指令被处理器执行时实现上述不确定度预测方法实施例的各个过程，且能达到相同的技术效果，为避免重复，这里不再赘述。
[0123]
其中，所述处理器为上述实施例中所述的电子设备中的处理器。所述可读存储介质，包括计算机可读存储介质，如计算机只读存储器(read-only memory，rom)、随机存取存储器(random access memory，ram)、磁碟或者光盘等。
[0124]
可以理解的是，以上实施方式仅仅是为了说明本技术的原理而采用的示例性实施方式，然而本技术并不局限于此。对于本领域内的普通技术人员而言，在不脱离本技术的精神和实质的情况下，可以做出各种变型和改进，这些变型和改进也视为本技术的保护范围。