一种电力负荷分解模型的建立方法及装置与流程

1.本发明涉及电力技术领域，尤其涉及一种电力负荷分解模型的建立方法及装置。


背景技术：

2.随着智能电网及人工智能物联网技术的高速发展，家庭能源消耗分析和基于用电情况的用户行为理解逐渐成为一个热点技术发展方向，目前，学术界提出了非侵入式负载检测(non-intrusive load monitoring，nilm)的技术概念，通过在主干路输电线上部署单一传感器并测量总的电流、电压数据来推测单个用电器的工作状态。现有技术中关于非侵入式电力负荷分解方法，主要基于非监督学习算法的隐马尔科夫模型及其扩展模型，它是针对离散序列，基于滑动窗技术提取相关特征，而后进行概率建模，并使用维特比算法实现负荷模型求解。但是该方法，存在以下问题：
3.1、隐马尔可夫模型的齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于某前一时刻的状态，与其他时刻的状态及观测无关。但实际中，当前时刻的状态不仅依赖于前一时刻的状态，且与其他时刻有关。
4.2、隐马尔可夫模型的观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测与状态无关。但实际中，当前时刻的观测并非只依赖于当前时刻的状态，而与之前时刻的观测也有关。
5.因此，隐马尔可夫模型存在不足，不符合现实情况。


技术实现要素：

6.本发明提供了一种电力负荷分解模型的建立方法及装置，能够克服目前隐马尔可夫及其拓展模型中对负荷序列以及观测序列的不合理假设，提高电力负荷分解的准确性。
7.一种电力负荷分解模型的建立方法，包括：
8.采集用户用电数据：
9.将所述用户用电数据作为训练集，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值；
10.根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，获得线性条件随机场模型作为电力负荷分解模型。
11.进一步地，所述用户用电数据包括单个负荷元件的有功功率。
12.进一步地，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值，包括：
13.将多个单个负荷元件的有功功率作为训练样本，并随机生成k个初始聚类中心点；
14.计算每个训练样本与所述初始聚类中心点的欧式距离，并将距离所述初始聚类中心点最近的预设数量个训练样本划分到对应的运行状态聚类中；
15.重新计算每个聚类的聚类中心点，并重新划分运行状态聚类，直到聚类中心点收
敛或者聚类次数达到预设次数，获得的最终聚类的聚类中心点为负荷相同工作状态下对应的有功功率的平均值。
16.进一步地，负荷的状态特征函数包括负荷相邻运行状态之间的状态转移特征函数t1,t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
；
17.所述模型的参数包括权值；
18.根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，包括：
19.将通过聚类获得的负荷相同工作状态下对应的有功功率的平均值作为状态序列s，将单个负荷元件的有功功率作为有功功率序列p；
20.将所述状态序列s和所述有功功率序列p作为训练集，获得联合经验分布
21.将所述联合经验分布负荷相邻运行状态之间的状态转移特征函数t1,t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
作为输入：
22.取权值ωk初始值为0，对每一k∈{1,2,
…
,k}：
23.当k＝1,2,
…
,k1时，令δk是方程
24.的解，k1表示状态转移特征的个数，t为时间序列总个数，p为有功功率，s为隐藏状态值，t表示时刻，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，tk(s
t-1
,s
t
,p,t)表示负荷相邻运行状态之间的状态转移特征函数，表示负荷相邻运行状态之间的状态转移特征函数关于联合经验分布的数学期望；
25.当k＝k1+l,l＝1,2,
…
,k2时，令δk是方程
26.的解，k2表示当前运行状态特征的个数，t为时间序列总个数，s
l
(s
t
,p,t)表示定义在结点上的运行状态特征函数，l为结点个数，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，表示结点上的当前运行状态特征函关于联合经验分布的数学期望；；
27.其中，t(p,s)由下式进行计算：
[0028][0029]
其中，k表示状态转移特征和当前运行状态特征个数的总和，n为训练集内数据个数，fk(s,p)表示特征函数的全局表达形式，m表示训练集内数据各个时刻的数据点，p为有功功率，s
m-1
表示前一时刻的隐藏状态值，sm表示当前时刻的隐藏状态值；
[0030]
根据计算的δk值，更新权值ωk：ωk←
ωk+δk，直到权值ωk收敛。
[0031]
进一步地，所述线性条件随机场模型p(s|p)通过以下形式表示：
[0032][0033][0034]
式中，fk(s，p)表示状态特征函数的全局表达形式，ωk表示权值，k表示状态转移特征和当前运行状态特征个数的总和，z(p)为规范化因子。
[0035]
进一步地，获得线性条件随机场模型作为电力负荷分解模型之后，还包括：
[0036]
结合用户用电数据和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列；
[0037]
根据所述最大概率的负荷元件运行状态序列对所述线性条件随机场模型进行评价。
[0038]
进一步地，结合用户用电数据和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列，包括：
[0039]
初始化，通过公式δ1(j)＝ω
·
f1(s0＝start,s1＝j,p),j＝1,2,
…
,m，求取t＝1时刻的非规范化概率，其中，δ1(j)为t＝1时刻的非规范化概率，p为有功功率，f1(s0＝start,s1＝j,p)表示在时刻t＝1的局部特征变量，j为标记变量，m为标记总量，ω为权值向量，ω＝(ω1,ω2,
…
,ωk)
t
；
[0040]
通过递推公式通过递推公式求解t＝i时刻非规范化概率最大值，其中，δi(q)为t＝i时刻非规范化概率最大值，q为标记变量，δ
i-1
(j)表示t＝i-1时刻的非规范化概率；
[0041]
通过递推公式通过递推公式记录非规范化概率最大值的路径ψi(q)；
[0042]
t＝n时终止，获得非规范化概率最大值非规范化概率最大值的路径的终点为
[0043]
返回非规范化概率最大值的路径2,
…
,1，求得最大概率的负荷元件运行状态序列为
[0044]
进一步地，根据所述最大概率的负荷元件运行状态序列对所述线性条件随机场模型进行评价，包括：
[0045]
分析预测得到的负荷元件状态序列与真实值之间的差值，利用平均绝对误差和均方根误差，对负荷分解结果的准确性进行评价。
[0046]
进一步地，绝对误差和均方根误差的计算公式如下：
[0047]
[0048][0049]
其中，maez表示负荷z的平均绝对误差，rmsez表示负荷z的均方根误差，表示负荷z在t时刻的预测值，表示负荷z在t时刻的真实值，n为训练集内数据个数。
[0050]
一种电力负荷分解模型的建立装置，包括：
[0051]
采集模块，用于采集用户用电数据：
[0052]
聚类模块，用于将所述用户用电数据作为训练集，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值；
[0053]
训练模块，用于根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，获得线性条件随机场模型作为电力负荷分解模型。
[0054]
本发明提供的电力负荷分解模型的建立方法及装置，至少包括如下有益效果：
[0055]
基于用户用电数据和电力负荷元件运行状态物理特征，借助于线性条件随机场，生成负荷元件状态特征方程和转移特征方程，最终实现负荷元件分解模型的建立，有效地提升了负荷建模的效率，利用状态特征和状态转移特征来描述负荷模型，克服了目前隐马尔可夫及其拓展模型中对负荷序列以及观测序列的不合理假设，提高负荷元件分解的准确性。
附图说明
[0056]
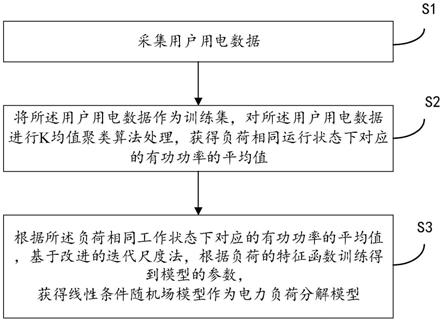
图1为本发明提供的电力负荷分解模型的建立方法一种实施例的流程图。
[0057]
图2为本发明提供的电力负荷分解模型的建立装置一种实施例的示意图。
具体实施方式
[0058]
为了更好的理解上述技术方案，下面将结合说明书附图以及具体的实施方式对上述技术方案做详细的说明。
[0059]
参考图1，在一些实施例中，提供一种电力负荷分解模型的建立方法，包括：
[0060]
s1、采集用户用电数据：
[0061]
s2、将所述用户用电数据作为训练集，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值；
[0062]
s3、根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，获得线性条件随机场模型作为电力负荷分解模型。
[0063]
其中，步骤s1中，采集的所述用户用电数据包括单个负荷元件的有功功率。
[0064]
其中，单个负荷元件的有功功率作为训练数据，可以通过设置在单个负荷元件的电路上的传感器采集得到，也可作为后续的测试数据，对模型进行评价。
[0065]
进一步地，步骤s2中，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值，包括：
[0066]
s21、将多个单个负荷元件的有功功率作为训练样本，并随机生成k个初始聚类中
心点；
[0067]
s22、计算每个训练样本与所述初始聚类中心点的欧式距离，并将距离所述初始聚类中心点最近的预设数量个训练样本划分到对应的运行状态聚类中；
[0068]
s23、重新计算每个聚类的聚类中心点，并重新划分运行状态聚类，直到聚类中心点收敛或者聚类次数达到预设次数，获得的最终聚类的聚类中心点为负荷相同工作状态下对应的有功功率的平均值。
[0069]
具体地，步骤s21中，训练样本为{q1,q2,
…
,qn}，其中每个qi∈rn，qi为单个负荷元件的有功功率，初始k个聚类中心点可随机产生，u1,u2,
…
,uk∈rn。
[0070]
步骤s22中，欧式距离通过以下公式进行计算：
[0071][0072]
步骤s23中，通过以下公式重新计算每个聚类的聚类中心点：
[0073][0074]
其中，表示类别j中所有样本的特征和，表示类别j中的样本的个数。
[0075]
进一步地，步骤s3中，负荷的状态特征函数包括负荷相邻运行状态之间的状态转移特征函数t1,t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
；
[0076]
状态转移特征函数和运行状态函数是根据实际给定的，状态转移特征函数tk(s
t-1
＝100,s
t
＝0,p,t)就表示当前时刻t输出功率为0，前一时刻输出功率为100w的一个函数，负荷当前运行状态特征函数表示负荷某一时刻的功率。
[0077]
所述模型的参数包括权值；
[0078]
根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，包括：
[0079]
将通过聚类获得的负荷相同工作状态下对应的有功功率的平均值作为状态序列s，将单个负荷元件的有功功率作为有功功率序列p；
[0080]
将所述状态序列s和所述有功功率序列p作为训练集，获得联合经验分布
[0081]
将所述联合经验分布负荷相邻运行状态之间的状态转移特征函数t1,t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
作为输入：
[0082]
取权值ωk初始值为0，对每一k∈{1,2,
…
,k}：
[0083]
当k＝1,2,
…
,k1时，令δk是方程
[0084]
的解，k1表示状态转移特征的个数，t为时间序列总个数，p为有功功率，s为隐藏状态值，t表示时刻，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，tk(s
t-1
,s
t
,p,t)表示负荷相邻运行状态之间的状态转移特征函数，表示负荷相邻运行状态之间的状态转移特征函数
关于联合经验分布的数学期望；
[0085]
当k＝k1+l,l＝1,2,
…
,k2时，令δk是方程
[0086]
的解，k2表示当前运行状态特征的个数，t为时间序列总个数，s
l
(s
t
,p,t)表示定义在结点上的状态特征函数，l为结点个数，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，表示结点上的当前运行状态特征函关于联合经验分布的数学期望；
[0087]
其中，t(p,s)由下式给出：
[0088][0089]
其中，k表示状态转移特征和当前运行状态特征个数的总和，n为训练集内数据个数，fk(s,p)表示特征函数的全局表达形式，m表示训练集内数据各个时刻的数据点，p为有功功率，s
m-1
表示前一时刻的隐藏状态值，sm表示当前时刻的隐藏状态值；
[0090]
根据计算的δk值，更新模型参数ωk：ωk←
ωk+δk，直到模型参数ωk收敛。
[0091]
进一步地，所述线性条件随机场设为p(s|p)，则在负荷观测有功功率p取值为p的条件下，负荷运行状态值s取值为s的条件概率的参数化形式如下所示：
[0092][0093][0094]
其中，tk(s
t-1
,s
t
,p,t)表示表示负荷相邻运行状态之间的状态转移特征函数；s
l
(s
t
,p,t)表示定义在结点上的运行状态特征函数，λk，μ
l
为可学习的参数，z(p)为规范化因子，t表示时间序列总长度，k表示具有直接联系的边的总个数，l表示结点总个数。
[0095]
将状态转移特征函数、当前运行状态特征函数以及权值用统一符号表示，设有k1个状态转移特征，k2个当前运行状态特征，k＝k1+k2：
[0096][0097]
然后，对状态转移特征与当前运行状态特征在各个时刻t求和，记作：
[0098][0099]
用ωk表示特征fk(s,p)的权值，
[0100][0101]
将状态转移特征函数、当前运行状态特征函数以及权值用统一符号表示，可将参数化形式转化为简化形式表示：
[0102][0103][0104]
式中，fk(s,p)表示特征函数的全局表达形式，ωk表示统一权值，k表示状态转移特征和当前运行状态特征个数的总和，z(p)为规范化因子。
[0105]
若以ω表示权值向量，即
[0106]
ω＝(ω1,ω2,
…
,ωk)
t
；
ꢀꢀꢀ
(11)
[0107]
以f(s,p)表示全局特征向量，即
[0108]
f(s,p)＝(f1(s,p),f2(s,p),
…
,fk(s,p))
t
；
ꢀꢀꢀ
(12)
[0109]
则线性条件随机场可以写成向量ω与f(s,p)的内积的形式：
[0110][0111][0112]
进一步地，获得线性条件随机场模型作为电力负荷分解模型之后，还包括：
[0113]
s4、结合用户用电数据和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列；
[0114]
s5、根据所述最大概率的负荷元件运行状态序列对所述线性条件随机场模型进行评价。
[0115]
其中，步骤s4中，结合用户用电总量时间序列采样值和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列，包括：
[0116]
初始化，通过公式δ1(j)＝ω
·
f1(s0＝start,s1＝j,p),j＝1,2,
…
,m，求取t＝1时刻的非规范化概率，其中，δ1(j)为t＝1时刻的非规范化概率，p为有功功率，f1(s0＝start,s1＝j,p)表示在时刻t＝1的局部特征变量，j为标记变量，m为标记总量，ω为权值向量，ω＝(ω1,ω2,
…
,ωk)
t
；
[0117]
通过递推公式通过递推公式求解t＝i时刻非规范化概率最大值，其中，δi(q)为t＝i时刻非规范化概率最大值，q为标记变量，δ
i-1
(j)表示t＝i-1时刻的非规范化概率；
[0118]
通过递推公式通过递推公式记录非规范化概率最大值的路径ψi(q)；
[0119]
t＝n时终止，获得非规范化概率最大值非规范化概率最大值的路径的终点为
[0120]
返回非规范化概率最大值的路径返回非规范化概率最大值的路径求得
最大概率的负荷元件运行状态序列为
[0121]
进一步地，步骤s5中，根据所述最大概率的负荷元件运行状态序列对所述线性条件随机场模型进行评价，包括：
[0122]
分析预测得到的负荷元件状态序列与真实值之间的差值，利用平均绝对误差和均方根误差，对负荷分解的结果准确度进行评价。
[0123]
其中，绝对误差和均方根误差的计算公式如下：
[0124][0125][0126]
其中，maez表示负荷z的平均绝对误差，rmsez表示负荷z的均方根误差，表示负荷z在t时刻的预测值，表示负荷z在t时刻的真实值，n为训练集内数据个数。
[0127]
误差表示分解值与精确值之间的距离，因此这两个数值越小，表明模型分解的准确度越高。
[0128]
参考图2，在一些实施例中，提供一种电力负荷分解模型的建立装置，包括：
[0129]
采集模块201，用于采集用户用电数据：
[0130]
聚类模块202，用于将所述用户用电数据作为训练集，对所述用户用电数据进行k均值聚类算法处理，获得负荷相同运行状态下对应的有功功率的平均值；
[0131]
训练模块203，用于根据所述负荷相同工作状态下对应的有功功率的平均值，基于改进的迭代尺度法，根据负荷的特征函数训练得到模型的参数，获得线性条件随机场模型作为电力负荷分解模型。
[0132]
具体地，采集模块201采集的用户用电数据包括单个负荷元件的有功功率。
[0133]
进一步地，聚类模块202还用于将多个单个负荷元件的有功功率作为训练样本，并随机生成k个初始聚类中心点；
[0134]
计算每个训练样本与所述初始聚类中心点的欧式距离，并将距离所述初始聚类中心点最近的预设数量个训练样本划分到对应的运行状态聚类中；
[0135]
重新计算每个聚类的聚类中心点，并重新划分运行状态聚类，直到聚类中心点收敛或者聚类次数达到预设次数，获得的最终聚类的聚类中心点为负荷相同工作状态下对应的有功功率的平均值。
[0136]
进一步地，负荷的特征函数包括负荷相邻运行状态之间的状态转移特征函数t1,t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
；
[0137]
训练模块203还用于：
[0138]
将通过聚类获得的负荷相同工作状态下对应的有功功率的平均值作为状态序列s，将单个负荷元件的有功功率作为有功功率序列p；
[0139]
将所述状态序列s和所述有功功率序列p作为训练集，获得联合经验分布
[0140]
将所述联合经验分布负荷相邻运行状态之间的状态转移特征函数t1,
t2,
…
,t
k1
以及负荷当前运行状态特征函数s1,s2,
…
,s
k2
作为输入：
[0141]
取权值ωk初始值为0，对每一k∈{1,2,
…
,k}：
[0142]
当k＝1,2,
…
,k1时，令δk是方程
[0143]
的解，k1表示状态转移特征的个数，t为时间序列总个数，p为有功功率，s为隐藏状态值，t表示时刻，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，tk(
t-1
,s
t
,p,t)表示负荷相邻运行状态之间的状态转移特征函数，表示负荷相邻运行状态之间的状态转移特征函数关于联合经验分布的数学期望；
[0144]
当k＝k1+l,l＝1,2,
…
,k2时，令δk是方程
[0145]
的解，k2表示当前运行状态特征的个数，t为时间序列总个数，s
l
(s
t
,p,t)表示定义在结点上的运行状态特征函数，l为结点个数，表示有功功率的经验概率分布，p(s|p)表示线性条件随机场模型，表示结点上的当前运行状态特征函关于联合经验分布的数学期望；
[0146]
其中，t(p,s)由下式进行计算：
[0147][0148]
其中，k表示状态转移特征和当前运行状态特征个数的总和，n为训练集内数据个数，fk(s,p)表示特征函数的全局表达形式，m表示训练集内数据各个时刻的数据点，p为有功功率，s
m-1
表示前一时刻的隐藏状态值，sm表示当前时刻的隐藏状态值；
[0149]
根据计算的δk值，更新权值ωk：ωk←
ωk+δk，直到权值ωk收敛。
[0150]
所述线性条件随机场模型p(s|p)通过以下形式表示：
[0151][0152][0153]
式中，fk(s,p)表示特征函数的全局表达形式，ωk表示权值，k表示状态转移特征和当前运行状态特征个数的总和，z(p)为规范化因子。
[0154]
进一步地，所述装置还包括评价模块204，用于结合用户用电数据和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列；根据所述最大概率的负荷元件运行状态序列对所述线性条件随机场模型进行评价。
[0155]
其中，结合用户用电数据和线性条件随机场模型，借助维比特算法，形成最大概率的负荷元件运行状态序列，包括：
[0156]
初始化，通过公式δ1(j)＝ω
·
f1(s0＝start,s1＝j,p),j＝1,2,
…
,m，求取t＝1时
刻的非规范化概率，其中，δ1(j)为t＝1时刻的非规范化概率，p为有功功率，f1(s0＝start,s1＝j,p)表示在时刻t＝1的局部特征变量，j为标记变量，m为标记总量，ω为权值向量，ω＝(ω1,ω2,
…
,ωk)
t
；
[0157]
通过递推公式通过递推公式求解t＝i时刻非规范化概率最大值，其中，δi(l)为t＝i时刻非规范化概率最大值，q为标记变量，δ
i-1
(j)表示t＝i-1时刻的非规范化概率；
[0158]
通过递推公式通过递推公式记录非规范化概率最大值的路径ψi(q)；
[0159]
t＝n时终止，获得非规范化概率最大值非规范化概率最大值的路径的终点为
[0160]
返回非规范化概率最大值的路径返回非规范化概率最大值的路径求得最大概率的负荷元件运行状态序列为
[0161]
进一步地，评价模块204还用于：分析预测得到的负荷元件状态序列与真实值之间的差值，利用平均绝对误差和均方根误差，对负荷分解结果的准确性进行评价。
[0162]
绝对误差和均方根误差的计算公式如下：
[0163][0164][0165]
其中，maez表示负荷z的平均绝对误差，rmsez表示负荷z的均方根误差，表示负荷z在t时刻的预测值，表示负荷z在t时刻的真实值，n为训练集内数据个数。
[0166]
本实施例提供的电力负荷分解模型的建立方法及装置，基于用户用电数据和电力负荷元件运行状态物理特征，借助于线性条件随机场，生成负荷元件状态特征方程和转移特征方程，最终实现负荷元件分解模型的建立，有效地提升了负荷建模的效率，利用状态特征和状态转移特征来描述负荷模型，克服了目前隐马尔可夫及其拓展模型中对负荷序列以及观测序列的不合理假设，提高负荷元件分解的准确性。
[0167]
尽管已描述了本发明的优选实施例，但本领域内的技术人员一旦得知了基本创造性概念，则可对这些实施例作出另外的变更和修改。所以，所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。