基于回声状态网络的多维时间序列缺失补全方法

1.本发明涉及数据补全领域，具体涉及一种基于回声状态网络的多维时间序列缺失补全方法。


背景技术：

2.随着物联网的不断普及，数十亿来自环境、建筑和智能设备的嵌入式传感器产生了大量的时间序列数据，为人类生活中的各种应用提供了强大的支持。然而，各种意外事故不可避免地会导致数据丢失，从而影响下游应用的决策能力。因此，对缺失值进行估计以提高数据质量往往是各种应用在数据预处理阶段中非常重要的一环。
3.缺失数据估计指的是使用统计或机器学习技术在缺失位置填充估计值的过程。根据考虑的数据相关性的不同，常用的方法大致可分为以下四类：插值法、归算法、基于矩阵的填充和基于深度学习的方法。第一类方法称为插值法，它利用时间序列中观测值之间的时间相关性来估计缺失值，最常见的有线性插值、三次样条插值、模糊插值和谱方法等。插值法的缺点是没有充分考虑影响时间序列的外生变量的跨域相关性。第二类方法称为归算法，它考虑了外生变量与观测值之间的相关性，并通过拟合两者的关系来生成估计值。常用的方法包括：基于距离的归算(k近邻或模糊聚类)，基于决策的归算(回归树或随机森林)，非线性归算(人工神经网络或支持向量机回归)，期望最大化归算和多重归算等。考虑到许多应用场景中的数据往往同时具有时间和跨域相关性，上述两种方法都存在丢失一些重要信息的风险。第三类方法是基于矩阵的填充，如低秩矩阵补全，矩阵分解等。此类方法把外生变量和观测值随时间变化的过程存储为一个矩阵再进行缺失值的填充。虽然此类方法可以充分利用矩阵中已有数据之间的相关性，但它需要满足一些很强的假设(如低秩性，时间平衡性，空间稳定性等)，而且它将时序数据视为静态数据，忽略了数据的时间成分。第四类方法则是基于目前流行的深度学习技术。其中擅长捕捉时序依赖关系的循环神经网络(recurrent neural network，rnn)尤为受到关注。但是，目前在缺失数据补全领域所采用的rnn架构都是基于门控机制的，如长短期记忆网络(long short term memory，lstm)和门控循环单元(gated recurrent unit，gru)。门的引入虽然可以缓解随时间反向传播(back propagation through time,bptt)的权重更新算法造成的梯度消失问题，但对训练数据量和计算成本都有很高的要求。这显然不适合具有大量缺失数据或实时性要求较高的应用。


技术实现要素：

4.有鉴于此，本发明的目的在于提供一种基于回声状态网络的多维时间序列缺失补全方法，基于全面的数据相关性来提升多维时间序列的补全精度。
5.为实现上述目的，本发明采用如下技术方案：
6.一种基于回声状态网络的多维时间序列缺失补全方法，包括以下步骤：
7.步骤s1：构建一个包含输入层、隐藏层和输出层的回声状态网络模型，并初始化；
8.步骤s2:按照时间顺序，向回声状态网络模型的输入层提供每个时刻的外生变量，
向输出层提供对应时刻的多维时间序列的观测值，若缺失的观测值尚未预补，则利用基于方向的最近邻策略进行暂时性预补；
9.步骤s3:根据使用的储备池个数的不同，分构建具有双向反馈的前向或双向回声状态网络，并利用不同的内部状态更新公式计算所有时刻的内部状态；
10.步骤s4:根据无需预补时刻的输入、内部状态和真实输出训练出网络的输出权重；
11.步骤s5:根据需要预补时刻的输入、内部状态和步骤s4得到的输出权重计算输出估计值，并用于对预补值进行更新；
12.步骤s6:重复步骤s3-s5直至,满足预设要求，迭代结束，用最后的预补值填补原始序列的缺失值。
13.进一步的，所述初始化，具体为：随机初始化网络的输入权重、反馈权重和循环权重，其中循环权重要求是稀疏的。
14.进一步的，所述步骤s1具体为：
15.步骤s11：构建一个包含输入层、隐藏层和输出层的回声状态网络，输入层神经元的个数ni与影响时间序列的外生变量的个数相同，隐藏层包含前向储备池，反向储备池和融合储备池，它们的神经元个数均为nr，输出层神经元的个数no与多维时间序列的维度相同；
16.步骤s12：利用[-1,1]的均匀分布随机生成输入层到前向储备池、反向储备池的输入全连接权重和前一时刻和后一时刻的输出层分别到当前时刻的前向储备池的反馈全连接权重和后一时刻的输出层到当前时刻的反向储备池的反馈全连接权重前一时刻到当前时刻的前向储备池的循环稀疏连接权重其非零元素的个数由稀疏率决定；后一时刻到当前时刻的反向储备池的循环稀疏连接权重其非零元素的个数由稀疏率决定；
[0017]
步骤s13：将权重矩阵w
i1
，w
i2
，w
f1
，w
f2
和w
f3
按照各自的缩放因子s
i1
，s
i2
，s
f1
，s
f2
和s
f3
进行缩放。将w
r1
和w
r2
按照各自的谱半径因子ρ
r1
和ρ
r2
根据公式(1)-(2)进行调整，其中λ
max
(w
r1
)和λ
max
(w
r2
)指的是w
r1
和w
r2
的最大特征值
[0018][0019][0020]
进一步的，所述利用基于方向的最近邻策略进行暂时性预补，具体为：
[0021]
步骤s21：已知原始时间序列y＝{y1，...，y
t
，...，y
l
}，l为时间序列的长度，其中
[0022]
根据y中的缺失情况，定义一个多维时间序列m＝{m1，
…
，m
t
，...，m
l
}，其中若时刻t的第j维的观测值是缺失的，则若是未缺失的，则
[0023]
步骤s22：在计算内部状态之前，已知外生变置之前，已知外生变置但输出时间序列中y
t-1
或中某些维度的观测值出现缺失，利用基于方向的最近邻策略进行初始预补。
[0024]
进一步的，所述基于方向的最近邻策略，具体为：
[0025]
若缺失，应该采用第j个观测值在历史时刻中最后一个未缺失的观测值对其进行预补，如公式(3)所示；若缺失，应该采用第j个观测值在后续时刻中最新一个未缺失的观测值进行预补，如公式(3)所示：
[0026][0027][0028]
其中，表示时刻t之前第j个观测值的最后一个未丢失时刻，表示时刻t之后第j个观测值的第一个未丢失时刻。
[0029]
进一步的，所述具有双向反馈的前向回声状态网络，具体为：只需要用到隐藏层的前向储备池，无需使用反向储备池，具有双向反馈的前向回声状态网络的状态更新方程如公式(5)所示：
[0030][0031]
其中，表示t时刻前向储备池的内部状态；f(.)为神经元的激活函数，通常是双曲正切函数tanh；[.；.]表示两个向量的上下联接；
[0032]
将每个时刻的内部状态h
t
，外生变量x
t
，输出观测值y
t
进行向量的上下拼接，得到扩展状态然后将所有时刻的z
t
按列存储成矩阵
[0033]
进一步的，所述具有双向反馈的双向回声状态网络，具体为：需要用到隐藏层的前向储备池，反向储备池和融合储备池。该模型的状态更新方程如公式(6)-(8)所示：
[0034]
[0035][0036][0037]
其中，表示t时刻反向储备池的内部状态；α∈[0，1]用于控制前向状态和反向状态之间的相对重要性。
[0038]
将每个时刻的内部状态h
t
，外生变量x
t
，输出观测值y
t
进行向量的上下拼接，得到扩展状态然后将所有时刻的z
t
按列存储成矩阵
[0039]
进一步的，所述步骤s4具体为：
[0040]
步骤s41：对于j∈{1，2，...，no}，从j＝1开始，重复执行步骤s42-s44，直至j＝no；
[0041]
步骤s42：对于t∈{1，2，...，l}，将矩阵h中所有对应时刻的行取出，得到矩阵为时间序列的第j维中未缺失的观测个数；
[0042]
步骤s43：取出中对应时间序列的第j维观测值的列，得到向量将剩余的部分命名为
[0043]
步骤s44：利用岭回归法求解公式(9)的优化函数，得到步骤s44：利用岭回归法求解公式(9)的优化函数，得到
[0044][0045]
进一步的，所述步骤s5具体为：
[0046]
步骤s51：对于j∈{1，2，...，no}，从j＝1开始，重复执行步骤s52-s55，直至j＝no；
[0047]
步骤s52：对于t∈{1，2，...，l}，将矩阵h中所有对应时刻的行取出，得到矩阵
[0048]
步骤s53：取出中对应时间序列的第j维观测值的列，得到向量将剩余的部分命名为
[0049]
步骤s54：利用步骤s44得到的根据公式(10)更新
[0050][0051]
步骤s55、将中的值按顺序填充到时间序列的第j维观测值的缺失位置。
[0052]
本发明与现有技术相比具有以下有益效果：
[0053]
本发明能够在有效降低模型训练复杂度的同时，实现对缺失数据的最佳填充。
附图说明
[0054]
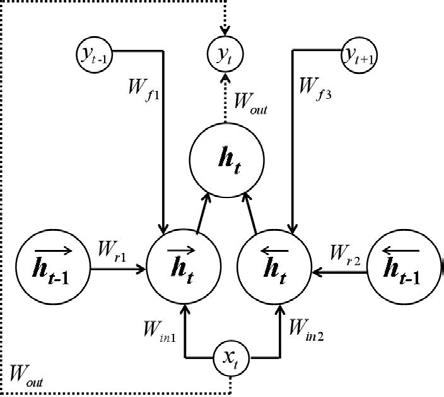
图1是本发明一实施例中具有双向反馈的前向回声状态网络；
[0055]
图2是本发明一实施例中具有双向反馈的双向回声状态网络。
具体实施方式
[0056]
下面结合附图及实施例对本发明做进一步说明。
[0057]
请参照图1和图2，本发明提供一种基于回声状态网络的多维时间序列缺失补全方法，包括以下步骤：
[0058]
步骤s1:构建一个包含输入层、隐藏层和输出层的回声状态网络模型，其中隐藏层包含前向储备池，反向储备池和融合储备池。随机初始化网络的输入权重、反馈权重和循环权重，其中循环权重要求是稀疏的；
[0059]
步骤s2:按照时间顺序，向回声状态网络模型的输入层提供每个时刻的外生变量，向输出层提供对应时刻的多维时间序列的观测值，若缺失的观测值尚未预补，则利用基于方向的最近邻策略进行暂时性预补；
[0060]
步骤s3：根据使用的储备池个数的不同，分构建具有双向反馈的前向或双向回声状态网络，并利用不同的内部状态更新公式计算所有时刻的内部状态；
[0061]
步骤s4：根据无需预补时刻的输入、内部状态和真实输出训练出网络的输出权重；
[0062]
步骤s5：根据需要预补时刻的输入、内部状态和步骤s4得到的输出权重计算输出估计值，并用于对预补值进行更新；
[0063]
步骤s6：重复步骤s3-s5直至，满足预设要求，迭代结束，用最后的预补值填补原始序列的缺失值。
[0064]
在本实施例中，回声状态网络的构建过程如下：
[0065]
步骤s11：构建一个包含输入层、隐藏层和输出层的回声状态网络，输入层神经元的个数ni与影响时间序列的外生变量的个数相同，隐藏层包含前向储备池，反向储备池和融合储备池，它们的神经元个数均为nr，输出层神经元的个数no与多维时间序列的维度相同；
[0066]
步骤s12：利用[-1，1]的均匀分布随机生成输入层到前向储备池、反向储备池的输入全连接权重和前一时刻和后一时刻的输出层分别到当前时刻的前向储备池的反馈全连接权重和后一时刻的输出层到当前时刻的反向储备池的反馈全连接权重前一时刻到当前时刻的前向储备池的循环稀疏连接权重其非零元素的个数由稀疏率决定；后一时刻到当前时刻的反向储备池的循环稀疏连接权重其非零元素的个数由稀疏率决定；
[0067]
步骤s13：将权重矩阵w
i1
，w
i2
，w
f1
，w
f2
和w
f3
按照各自的缩放因子s
i1
，s
i2
，s
f1
，s
f2
和s
f3
进行缩放。将w
r1
和w
r2
按照各自的谱半径因子ρ
r1
和ρ
r2
根据公式(1)-(2)进行调整，其中λ
max
(w
r1
)和λ
max
(w
r2
)指的是w
r1
和w
r2
的最大特征值
[0068][0069][0070]
在本实施例中，利用基于方向的最近邻策略进行暂时性预补，具体为：
[0071]
步骤s21：已知原始时间序列y＝{y1，...，y
t
，...，y
l
}，l为时间序列的长度，其中
[0072]
根据y中的缺失情况，定义一个多维时间序列m＝{m1，...，mt，...，m
l
}，其中若时刻t的第j维的观测值是缺失的，则若是未缺失的，则
[0073]
步骤s22：在计算内部状态之前，已知外生变量之前，已知外生变量但输出时间序列中y
t-1
或中某些维度的观测值出现缺失，利用基于方向的最近邻策略进行初始预补。
[0074]
在本实施例中，基于方向的最近邻策略，具体为：
[0075]
若缺失，应该采用第j个观测值在历史时刻中最后一个未缺失的观测值对其进行预补，如公式(3)所示；若缺失，应该采用第j个观测值在后续时刻中最新一个未缺失的观测值进行预补，如公式(3)所示：
[0076][0077][0078]
其中，表示时刻t之前第j个观测值的最后一个未丢失时刻，表示时刻t之后第j个观测值的第一个未丢失时刻。
[0079]
在本发明一实施例中，步骤s3中，两种不同的网络模型的内部状态的具体计算方法如下：
[0080]
1)具有双向反馈的前向回声状态网络(esn with bidirectional feedback，esn-bf)
[0081]
步骤s31、该模型只需要用到隐藏层的前向储备池，无需使用反向储备池，具有双向反馈的前向回声状态网络的状态更新方程如公式(5)所示：
[0082][0083]
其中，表示t时刻前向储备池的内部状态；f(.)为神经元的激活函数，通常是双曲正切函数tanh；[.；.]表示两个向量的上下联接；
[0084]
步骤s32、将每个时刻的内部状态h
t
，外生变量x
t
，输出观测值y
t
进行向量的上下拼接，得到扩展状态然后将所有时刻的z
t
按列存储成矩阵
[0085]
2)具有双向反馈的双向回声状态网络(bidirectional esn with bidirectional feedback，besn-bf)
[0086]
步骤s31：该模型需要用到隐藏层的前向储备池，反向储备池和融合储备池。该模型的状态更新方程如公式(6)-(8)所示：
[0087][0088][0089][0090]
其中，表示t时刻反向储备池的内部状态；α∈[0，1]用于控制前向状态和反向状态之间的相对重要性。
[0091]
步骤s32、将每个时刻的内部状态h
t
，外生变量x
t
，输出观测值y
t
进行向量的上下拼接，得到扩展状态然后将所有时刻的z
t
按列存储成矩阵
[0092]
在本实施例中，步骤s4具体为：
[0093]
步骤s41：对于j∈{1，2，...，no}，从j＝1开始，重复执行步骤s42-s44，直至j＝no；
[0094]
步骤s42：对于t∈{1，2，...，l}，将矩阵h中所有对应时刻的行取出，得到矩阵为时间序列的第j维中未缺失的观测个数；
[0095]
步骤s43：取出中对应时间序列的第j维观测值的列，得到向量将剩余的部分命名为
[0096]
步骤s44：利用岭回归法求解公式(9)的优化函数，得到步骤s44：利用岭回归法求解公式(9)的优化函数，得到
[0097][0098]
在本实施例中，步骤s5具体为：
[0099]
步骤s51：对于j∈{1，2，...，no}，从j＝1开始，重复执行步骤s52-s55，直至j＝no；
[0100]
步骤s52：对于t∈{1，2，...，l}，将矩阵h中所有对应时刻的行取出，得到矩阵
[0101]
步骤s53：取出中对应时间序列的第j维观测值的列，得到向量将剩余的部分命名为
[0102]
步骤s54：利用步骤s44得到的根据公式(10)更新
[0103][0104]
步骤s55、将中的值按顺序填充到时间序列的第j维观测值的缺失位置。
[0105]
在本实施例中，步骤s6，还进一步计算补全性能指标，具体实现方法如下：
[0106]
步骤s601、根据公式(11)-(13)计算标准均方根误差(normalized root mean square error，nrmse)：
[0107][0108][0109][0110]
其中，和分别表示时间序列的第j维观测值在时刻t的估计值和真实值；
[0111]
步骤s602、根据公式(14)计算确定系数r2：
[0112][0113]
步骤s603、记录模型的运行时间。
[0114]
步骤s6054、评价模型的性能，其中nrmse和运行时间均是越小越好；而r2是对估计的回归方程拟合优度的度量，其值越大越好。
[0115]
以上所述仅为本发明的较佳实施例，凡依本发明申请专利范围所做的均等变化与修饰，皆应属本发明的涵盖范围。