一种基于横观各项同性虚拟材料的固定结合面等效模型建立方法

1.本发明属于固定结合面有限元模型技术领域，具体涉及一种基于横观各项同性虚拟材料的固定结合面等效模型建立方法。


背景技术：

2.固定结合面是指部件之间相互接触保持相对静止而不发生相对移动的机械结合面。固定结合面起着传递力和振动的作用，在外载荷作用下会产生不同程度的相互挤压和滑移，使得结合面具有刚度和阻尼的特性，该特性对于结构的动力学响应计算精度至关重要。在含有固定结合面的组合结构有限元模型中，往往是通过简化结合面的连接而建立其等效模型，其中虚拟材料法是一种新颖的等效模型建立方法，该虚拟材料指的是常见的各向同性虚拟材料。但其未考虑结合面法向和切向的不同连接特性，对结构的动力学响应计算精度产生了一定的影响。建立合理的等效模型是固定结合面问题的重要基础性工作，建立了等效模型之后，就需要采用合理的方法确定等效模型中的参数，对其进行修正改善。


技术实现要素：

3.本发明的目的在于解决现有结合面连接问题技术的不足，实现对固定结合面进行精确的建模分析的一种基于横观各项同性虚拟材料的固定结合面等效模型建立方法。
4.一种基于横观各向同性虚拟材料的固定结合面等效建模方法，包括以下步骤：
5.步骤1：在结构的有限元模型中，采用横观各向同性虚拟材料层单元代替由两个相互接触的部件所构成的固定结合面，以构建固定结合面等效模型。
6.所述的横观各向同性虚拟材料层单元在结合面的切向平面内具有相同的性能，并且与法向性能不同，这与各向同性虚拟材料所不同，其考虑了结合面法向和切向不同连接特性。横观各向同性虚拟材料层单元与两个相互接触的部件之间是直接刚性连接。
7.步骤2：根据横观各向同性材料的本构方程和固定结合面连接参数，建立虚拟材料层参数计算模型。
8.所述的虚拟材料层参数共有12个，分别为弹性模量e
x
,ey,ez，剪切模量g
yz
,g
xz
,g
xy
，泊松比μ
yz
,μ
xz
,μ
xy
，厚度h，密度ρ和阻尼系数η。鉴于虚拟材料层是横观各向同性材料，有e
x
＝ey,g
yz
＝g
xz
,μ
yz
＝μ
xz
以及g
xy
＝e
x
/(2+2μ
xy
)。
9.虚拟材料层弹性模量e
x
,ey,ez计算公式为：
[0010][0011][0012]
其中，e1,e2是两个相互接触部件的弹性模量，μ1,μ2是两个相互接触部件的泊松
比，σn,εn是虚拟材料层的法向应力和应变，kn是结合面单位面积法向刚度，h是虚拟材料层厚度。
[0013]
虚拟材料层剪切模量g
yz
,g
xz
,计算公式为：
[0014][0015][0016]
其中，τ,γ是虚拟材料层的法向应力和应变，k
τ
是结合面单位面积切向刚度。
[0017]
结合面在切向平面内承受拉压载荷时，法向产生的变形主要用于填补结合面微观微凸体之间的间隙，因此忽略法向产生的变形，所以有μ
yz
＝μ
xz
＝0。同理，忽略切向产生的变形，所以有μ
xy
＝0。
[0018]
虚拟材料层厚度h的计算公式为：
[0019]
h＝h1+h2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0020]
其中，h1,h2是两个相互接触部件表面微观微凸体厚度。
[0021]
虚拟材料层密度ρ计算公式为：
[0022][0023]
其中，m1,m2是两个相互接触部件表面微观微凸体质量，ρ1,ρ2是两个相互接触部件表面微观微凸体密度，v是虚拟材料层的体积，a是结合面的接触面积。
[0024]
虚拟材料层阻尼系数η的计算公式为：
[0025]
η＝η0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0026]
其中，η0是阻尼系数常数，其值与结合面的润滑条件，表面粗糙度等因素有关。
[0027]
步骤3：根据固定结合面连接参数，确定上述虚拟材料层中的已知参数及待定参数。
[0028]
所述的虚拟材料层已知参数为：两个相互接触部件的泊松比μ1,μ2，弹性模量e1,e2以及表面微观微凸体厚度h1,h2，密度ρ1,ρ2。其值通过部件本身的材料属性参数获得，其中厚度与表面粗糙度有关。所述的虚拟材料层待定参数为：结合面单位面积法向刚度和切向刚度kn,k
τ
以及阻尼系数η。
[0029]
步骤4：对含有结合面的组合结构进行模态试验分析，获得试验固有频率和阻尼比。
[0030]
步骤5：基于步骤1的固定结合面等效模型建立组合结构的参数化有限元模型，其设计变量为待定参数kn,k
τ
和η0。
[0031]
步骤6：基于步骤5的组合结构的参数化有限元模型进行模态仿真分析，获取计算固有频率和阻尼比。
[0032]
步骤7：基于步骤4的试验固有频率和阻尼比以及步骤6的计算固有频率和阻尼比建立目标函数。
[0033]
目标函数f为：
[0034][0035]
其中，m是模态的阶数，是试验固有频率和阻尼比，是计算固有频率和阻尼比。
[0036]
当试验固有频率和阻尼比与计算固有频率和阻尼比很接近或相等时，认为虚拟材料层能够表示真实结合面的连接特性。
[0037]
步骤8：基于优化算法对步骤7的目标函数f进行优化，进而对待定参数kn,k
τ
和η0进行识别。
[0038]
优化算法通过调用步骤5和步骤6来计算目标函数的值，实现了仿真的集成。优化的设计变量初始范围根据实际经验确定，优化终止条件为：
[0039]
|f
i-f
i-1
|≤tol
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0040]
其中，fi是当前迭代步的目标函数值，f
i-1
是上一迭代步的目标函数值，tol是容许偏差。
[0041]
步骤9：基于步骤8的优化识别结果，结合步骤3可确定虚拟材料层的所有参数。
[0042]
将步骤8得到的设计变量kn,k
τ
和η0最优值带入式(2)、(3)、(7)得ez,g
yz
和η，结合步骤3的已知参数，可确定虚拟材料层的所有参数。
[0043]
本发明的有益效果在于：
[0044]
(1)本发明的固定结合面等效模型建立方法是基于横观各向同性虚拟材料，相比于普通的虚拟材料方法考虑结合面法向和切向不同连接特性，与实际情况更相符，可以提升动力学响应计算精度。
[0045]
(2)本发明的等效模型参数确定方法的是参数化集成式的，可以大大节约计算时间，具有实用价值。参数确定只需要进行模态分析，一方面模态试验不需要设计专有实验装置，另一方面模态仿真计算较快，具有通用便捷性。
附图说明
[0046]
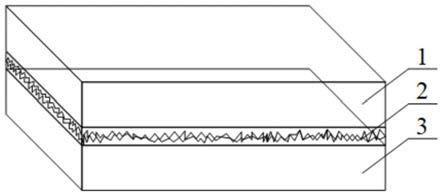
图1是本发明提供的两个部件构成的固定机械结合面示意图。
[0047]
图2是本发明提供的等效模型建立和参数确定方法的流程示意图。
[0048]
图3是本发明提供的带有参数的横观各项同性虚拟材料等效模型示意图。
[0049]
图中标号对应名称为：
[0050]
1、部件1；2、固定机械结合面；3、部件2；4、横观各向同性虚拟材料层。
具体实施方式
[0051]
下面结合附图对本发明做进一步描述。
[0052]
本实施例以图1所示的两个部件构成的固定机械结合面为例，采用本发明对该固定机械结合面进行等效建模和参数确定，如图2所示，具体按照以下步骤实现：
[0053]
步骤1：在结构的有限元模型中，采用横观各向同性虚拟材料层单元代替由两个相互接触的部件所构成的固定结合面，以构建固定结合面等效模型。
[0054]
步骤2：根据横观各向同性材料的本构方程和固定结合面连接参数，建立虚拟材料层参数计算模型，如图3所示。
[0055]
所述的虚拟材料层参数共有12个，分别为弹性模量e
x
,ey,ez，剪切模量g
yz
,g
xz
,g
xy
，泊松比μ
yz
,μ
xz
,μ
xy
，厚度h，密度ρ和阻尼系数η。鉴于虚拟材料层是横观各向同性材料，有e
x
＝ey,g
yz
＝g
xz
,μ
yz
＝μ
xz
以及g
xy
＝e
x
/(2+2μ
xy
)。
[0056]
虚拟材料层弹性模量e
x
,ey,ez计算公式为：
[0057][0058][0059]
其中，e1,e2是两个相互接触部件的弹性模量，μ1,μ2是两个相互接触部件的泊松比，σn,εn是虚拟材料层的法向应力和应变，kn是结合面单位面积法向刚度，h是虚拟材料层厚度。
[0060]
虚拟材料层剪切模量g
yz
,g
xz
,g
xy
计算公式为：
[0061][0062][0063]
其中，τ,γ是虚拟材料层的法向应力和应变，k
τ
是结合面单位面积切向刚度。
[0064]
结合面在切向平面内承受拉压载荷时，法向产生的变形主要用于填补结合面微观微凸体之间的间隙，因此忽略法向产生的变形，所以有μ
yz
＝μ
xz
＝0。同理，忽略切向产生的变形，所以有μ
xy
＝0。
[0065]
虚拟材料层厚度h的计算公式为：
[0066]
h＝h1+h2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0067]
其中，h1,h2是两个相互接触部件表面微观微凸体厚度。
[0068]
虚拟材料层密度ρ计算公式为：
[0069][0070]
其中，m1,m2是两个相互接触部件表面微观微凸体质量，ρ1,ρ2是两个相互接触部件表面微观微凸体密度，v是虚拟材料层的体积，a是结合面的接触面积。
[0071]
虚拟材料层阻尼系数η的计算公式为：
[0072]
η＝η0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0073]
其中，η0是阻尼系数常数，其值与结合面的润滑条件，表面粗糙度等因素有关。
[0074]
步骤3：根据固定结合面连接参数，确定上述虚拟材料层中的已知参数及待定参数。
[0075]
所述的虚拟材料层已知参数为：两个相互接触部件的泊松比μ1,μ2，弹性模量e1,e2以及表面微观微凸体厚度h1,h2，密度ρ1,ρ2。其值通过部件本身的材料属性参数获得，其中
厚度与表面粗糙度有关。所述的虚拟材料层待定参数为：结合面单位面积法向刚度和切向刚度kn,k
τ
以及阻尼系数η。
[0076]
步骤4：对含有结合面的组合结构进行模态试验分析，获得试验固有频率和阻尼比。
[0077]
步骤5：基于步骤1的固定结合面等效模型建立组合结构的参数化有限元模型，其设计变量为待定参数kn,k
τ
和η0。
[0078]
步骤6：基于步骤5的组合结构的参数化有限元模型进行模态仿真分析，获取计算固有频率和阻尼比。
[0079]
步骤7：基于步骤4的试验固有频率和阻尼比以及步骤6的计算固有频率和阻尼比建立目标函数。
[0080]
目标函数f为：
[0081][0082]
其中，m是模态的阶数，是试验固有频率和阻尼比，是计算固有频率和阻尼比。
[0083]
当试验固有频率和阻尼比与计算固有频率和阻尼比很接近或相等时，认为虚拟材料层能够表示真实结合面的连接特性。
[0084]
步骤8：基于优化算法对步骤7的目标函数f进行优化，进而对待定参数kn,k
τ
和η0进行识别。
[0085]
优化算法通过调用步骤5和步骤6来计算目标函数的值，实现了仿真的集成。优化的设计变量初始范围根据实际经验确定，优化终止条件为：
[0086]
|f
i-f
i-1
|≤tol
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0087]
其中，fi是当前迭代步的目标函数值，f
i-1
是上一迭代步的目标函数值，tol是容许偏差。
[0088]
步骤9：基于步骤8的优化识别结果，结合步骤3可确定虚拟材料层的所有参数。
[0089]
将步骤8得到的设计变量kn,k
τ
和η0最优值带入式(11)、(3)、(7)得ez,g
yz
和η，结合步骤3的已知参数，确定虚拟材料层的所有参数。
[0090]
本实施例中，以两个部件构成的固定机械结合面为例，基于横观各向同性虚拟材料等效模型建立组合结构的参数化有限元模型，通过试验和计算的模态数据构建目标函数，借助优化算法对等效模型中待定参数进行了确定。
[0091]
以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。