基于扩散-对流模型的海底混凝土隧道耐久寿命预测方法

1.本发明属于海底混凝土隧道耐久寿命预测领域，尤其涉及一种基于扩散-对流模型的海底混凝土隧道耐久寿命预测方法。


背景技术：

2.海底隧道是不可逆的重要工程，设计使用年限一般要求在100年以上。海底隧道长期处于高压力海水侵蚀的恶劣环境，氯离子侵蚀是其耐久寿命劣化的重要因素之一。氯离子在混凝土中的传输方式和传输速度是影响海底隧道耐久寿命的关键。目前国内外学者提出了多种基于氯离子扩散理论的海底隧道耐久寿命预测理论模型，以及采用遗传算法等隐式模糊预测模型。这些模型通常对氯离子扩散系数进行了多因素修正，然后基于fick第一和第二扩散定律进行确定性或考虑模型不确定性的可靠度研究。
3.混凝土是一种孔隙材料，氯离子在混凝土孔隙溶液中除了依靠浓度梯度驱动的扩散方式外，还会以孔隙水为载体通过对流作用一起运移，包括压力渗透作用、毛细作用等。目前对海底隧道中氯离子的扩散-对流研究，有学者根据duracrete模型直接在fick扩散模型中设置了对流层深度来实现，也有学者考虑压力渗透作用下的饱和混凝土扩散-对流模型，基于fick扩散定律和darcy定律建立了考虑海水压力渗透作用的扩散-对流模型，并采用ogata&banks的解析解进行分析。丹麦、瑞典等水下混凝土工程的取芯实验发现，即使服役了数十年的水下结构，也仅在距表面30mm深度内孔隙液态水含量完全饱和，超过该深度的混凝土处于非饱和状态。非饱和混凝土中水分运动的主要驱动势是反映毛细吸收作用的基质势，相应地非饱和混凝土中氯离子的扩散-对流模型应同时考虑扩散、外水压力和基质势作用。
4.综上所述，目前还没有基于非饱和混凝土中氯离子传输机制的扩散-对流模型应用于海底隧道耐久寿命预测的研究成果；目前通常采用氯离子扩散模型来预测海底隧道耐久寿命，忽略了海底隧道服役环境中外水压力，以及水下非饱和混凝土的毛细吸力作用对混凝土孔隙中水分的对流驱动，因此可能低估了海底隧道中自由氯离子的浓度，相应的可能高估了海底隧道的耐久寿命。


技术实现要素：

5.本发明的目的是克服现有技术中的不足，提供一种基于扩散-对流模型的海底混凝土隧道耐久寿命预测方法：
6.步骤1、建立海底隧道非饱和混凝土中氯离子扩散-对流模型；
7.步骤1.1、基于fick第一和第二定律，将混凝土孔隙溶液中自由氯离子的扩散通量作为扩散模型；
8.[0009][0010]
上式中，jd为自由氯离子的扩散通量，单位为kg/(m2s)；为nabla算子；cf为孔隙溶液中自由氯离子浓度，单位为kg/m3；t为扩散时间，单位为s；d
eff
为氯离子有效扩散系数，单位为m2/s；
[0011]
根据atkinson和nickerson模型，氯离子的有效扩散系数为：
[0012]deff
＝d
s0
φβ
[0013]
上式中，d
s0
为饱和混凝土的氯离子扩散系数，单位符号为m2/s；φ为孔隙率；β为孔结构参数β；
[0014]
孔结构参数为：
[0015]
β＝φ
1/3s10/3
[0016]
上式中：s为孔隙水饱和度；
[0017]
步骤1.2、将混凝土孔隙溶液中自由氯离子的对流通量jc作为对流模型；
[0018]
jc＝-cfu
[0019]
上式中，jc为自由氯离子的对流通量，单位为kg/(m2s)；u为混凝土孔隙中水的流速，单位为m/s；
[0020]
u按下式计算：
[0021][0022]
上式中：ks为饱和渗透系数，单位为m/s；ρw为水的密度，单位为kg/m3；g为重力加速度，单位为m/s2；kr为相对渗透率，0≤kr≤1，0代表完全干燥，1代表完全饱和；θ为含水率；ψ为驱动势，ψ＝ψm+ψ
p
，单位为pa；其中ψ
p
为渗流路径两侧压力差形成的压力势，单位为pa；ψm为单位容积水分的基质势，单位为pa；kr(θ)表示相对渗透率的大小与含水率的关系；
[0023]
单位容积水分的基质势ψm的计算模型为：
[0024]
ψm＝-α(s-1/m-1)
1-m
[0025]
上式中：α，m为混凝土材料的经验参数；
[0026]
步骤1.3、将总的自由氯离子通量j
cl
作为非饱和混凝土中氯离子扩散-对流模型：
[0027][0028]
上式中，j
cl
为总的自由氯离子通量，单位为kg/(m2s)；
[0029]
步骤2、判别海底隧道保护层处的最危险点；
[0030]
步骤3、进行海底隧道耐久寿命预测；取海底隧道保护层处的最危险点氯离子浓度cf(x，t)达到临界自由氯离子浓度cr的最短时间，作为海底隧道耐久寿命t1；cf(x，t)表示扩散时间t时刻距隧道外壁的距离x处的孔隙溶液中自由氯离子浓度cf；cf(x，t)由步骤1中的扩散-对流模型计算得到。
[0031]
作为优选，步骤1.2中，当混凝土处于完全饱和状态时，混凝土孔隙中水的流速u由darcy定律计算：
[0032][0033]
作为优选，步骤1.2中，当混凝土处于非饱和状态时，混凝土孔隙中水的流速u由richards方程计算：
[0034][0035]
作为优选，步骤2具体包括以下步骤：
[0036]
步骤2.1、首先根据海底隧道外壁初始时刻的水头压力p0，以及混凝土初始饱和度s，分别计算各点处的渗流路径两侧压力差形成的压力势ψ
p
和单位容积水分的基质势ψm；t为扩散时间；
[0037]
步骤2.2、将步骤2.1计算得到的ψ
p
、ψm代入对流模型jc＝-cfu，采用积分有限差分法计算得到下一个时间节点的混凝土孔隙中水的流速u和混凝土孔隙水饱和度s；
[0038]
步骤2.3、代入海底隧道外壁初始氯离子浓度和隧道内混凝土的初始氯离子浓度，计算得到第一个时间节点各位置处的对流通量jc、内外氯离子浓度梯度确定的扩散通量jd，以及总的自由氯离子通量j
cl
；并将jc、jd和j
cl
作为下一个时间节点计算的初始数据；
[0039]
步骤2.4、返回执行步骤2.1至步骤2.3，获得任意时间节点任意位置处的自由氯离子浓度值；最后将海底隧道保护层处氯离子浓度cf(x，t)最大的点作为整个海底隧道保护层处的最危险点；cf(x，t)表示扩散时间t时刻距隧道外壁的距离x处的孔隙溶液中自由氯离子浓度cf；cf(x，t)由步骤1中的扩散-对流模型计算得到。
[0040]
本发明的有益效果是：
[0041]
本发明是一种从外水压力作用下非饱和混凝土中氯离子传输机制入手，采用扩散-对流模型预测海底隧道耐久寿命的方法，该预测方法准确性更高，为海底隧道的耐久性设计提供科学的依据，对工程的耐久性能维护管理具有指导作用，并且为今后的海底混凝土隧道耐久设计研究提供了理论基础。
[0042]
本发明基于非饱和混凝土中氯离子传输机制建立了海底隧道非饱和混凝土中氯离子输运的扩散-对流模型，通过分析任意时间节点任意位置处的自由氯离子浓度分布，来确定隧道结构保护层位置处自由氯离子浓度最大的危险点，以及该点浓度达到临界氯离子浓度的服役时长，本发明可以适用于多种工况，包括不同环境自由浓度的海域、以及海底隧道的不同水头和混凝土初始饱和度。
附图说明
[0043]
图1-1至图1-4分别为本发明隧道管段内第10年、第50年、第100年、第133年的氯离子分布云图和最危险点示意图；
[0044]
图2为本发明不同水头压力下危险点处氯离子浓度变化图和隧道耐久寿命曲线图；
[0045]
图3为本发明不同混凝土初始饱和度下危险点处氯离子浓度变化图和隧道耐久寿命曲线图；
[0046]
图4为本发明不同环境自由氯离子浓度下危险点处氯离子浓度变化图和隧道耐久寿命曲线图；
[0047]
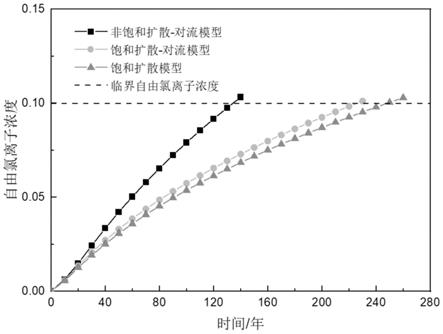
图5为本发明扩散模型、饱和扩散-对流模型、非饱和扩散-对流模型下危险点处氯离子浓度变化图和隧道耐久寿命曲线图。
具体实施方式
[0048]
下面结合实施例对本发明做进一步描述。下述实施例的说明只是用于帮助理解本发明。应当指出，对于本技术领域的普通人员来说，在不脱离本发明原理的前提下，还可以对本发明进行若干修饰，这些改进和修饰也落入本发明权利要求的保护范围内。
[0049]
本技术实施例一提供了一种基于扩散-对流模型的海底混凝土隧道耐久寿命预测方法：
[0050]
步骤1、考虑海底隧道的服役环境特点和混凝土的非饱和特性，建立海底隧道非饱和混凝土中氯离子扩散-对流模型；
[0051]
步骤1.1、基于fick第一和第二定律，将混凝土孔隙溶液中自由氯离子的扩散通量作为扩散模型；
[0052][0053][0054]
上式中，jd为自由氯离子的扩散通量，单位为kg/(m2s)；为nabla算子；cf为孔隙溶液中自由氯离子浓度，单位为kg/m3；t为扩散时间，单位为s；d
eff
为氯离子有效扩散系数，单位为m2/s；
[0055]
根据atkinson和nickerson模型，氯离子的有效扩散系数为：
[0056]deff
＝d
s0
φβ
[0057]
上式中，d
s0
为饱和混凝土的氯离子扩散系数，单位符号为m2/s；φ为孔隙率；β为孔结构参数β；
[0058]
孔结构参数为：
[0059]
β＝φ
1/3s10/3
[0060]
上式中：s为孔隙水饱和度；
[0061]
步骤1.2、将混凝土孔隙溶液中自由氯离子的对流通量jc作为对流模型；
[0062]
jc＝-cfu
[0063]
上式中，jc为自由氯离子的对流通量，单位为kg/(m2s)；u为混凝土孔隙中水的流速，单位为m/s；
[0064]
u按下式计算：
[0065][0066]
上式中：ks为饱和渗透系数，单位为m/s；ρw为水的密度，单位为kg/m3；g为重力加速度，单位为m/s2；kr为相对渗透率，0≤kr≤1，0代表完全干燥，1代表完全饱和；θ为含水率；ψ为驱动势，ψ＝ψm+ψ
p
，单位为pa；其中ψ
p
为渗流路径两侧压力差形成的压力势，单位为pa；ψm为单位容积水分的基质势，单位为pa；kr(θ)表示相对渗透率的大小与含水率的关系；
[0067]
单位容积水分的基质势ψm的计算模型为：
[0068]
ψm＝-α(s-1/m-1)
1-m
[0069]
上式中：α，m为混凝土材料的经验参数；
[0070]
当混凝土处于完全饱和状态时，混凝土孔隙中水的流速u由darcy定律计算：
[0071][0072]
当混凝土处于非饱和状态时，混凝土孔隙中水的流速u由richards方程计算：
[0073][0074]
步骤1.3、海底隧道外壁接触海水，内壁接触大气，内外氯离子浓度梯度会引起扩散通量jd；海底隧道混凝土在初始服役时处于非饱和状态，随着海水入渗混凝土饱和度逐渐提高，内部逐渐形成饱和区和非饱和区，对流通量jc的驱动势也会从基质势向压力势转换；因此海底隧道混凝土中氯离子传输受到扩散和对流共同驱动，将总的自由氯离子通量j
cl
作为非饱和混凝土中氯离子扩散-对流模型：
[0075][0076]
上式中，j
cl
为总的自由氯离子通量，单位为kg/(m2s)；
[0077]
步骤2、判别海底隧道保护层处的最危险点；
[0078]
步骤2.1、首先根据海底隧道外壁初始时刻(t＝0)的水头压力p0，以及混凝土初始饱和度s，分别计算各点处的渗流路径两侧压力差形成的压力势ψ
p
和单位容积水分的基质势ψm；t为扩散时间；
[0079]
步骤2.2、将步骤2.1计算得到的ψ
p
、ψm代入对流模型jc＝-cfu，采用积分有限差分法计算得到下一个时间节点(t＝1)的混凝土孔隙中水的流速u和混凝土孔隙水饱和度s；
[0080]
步骤2.3、代入海底隧道外壁初始氯离子浓度和隧道内混凝土的初始氯离子浓度，计算得到第一个时间节点各位置处的对流通量jc、内外氯离子浓度梯度确定的扩散通量jd，以及总的自由氯离子通量j
cl
；并将jc、jd和j
cl
作为下一个时间节点计算的初始数据；
[0081]
步骤2.4、返回执行步骤2.1至步骤2.3，获得任意时间节点任意位置处的自由氯离子浓度值；最后将海底隧道保护层处氯离子浓度cf(x，t)最大的点作为整个海底隧道保护层处的最危险点；cf(x，t)表示扩散时间t时刻距隧道外壁的距离x处的孔隙溶液中自由氯离子浓度cf；cf(x，t)由步骤1中的扩散-对流模型计算得到。
[0082]
步骤3、进行海底隧道耐久寿命预测；取海底隧道保护层处的最危险点氯离子浓度cf(x，t)达到临界自由氯离子浓度cr的最短时间，作为海底隧道耐久寿命t1。
[0083]
本实施例可以根据海底隧道服役环境的水头压力p0和环境自由氯离子浓度cs(x)，以及混凝土的材料参数，如初始饱和度s0、孔隙率φ、饱和渗透系数ks、氯离子有效扩散系数d
eff
等分别建立氯离子输运的扩散模型和扩散-对流模型，计算得到任意时间节点任意位置处的自由氯离子浓度值cf(x，t)；cf(x，t)表示扩散时间t时刻距隧道外壁的距离x处的孔隙溶液中自由氯离子浓度cf；cf(x，t)由步骤1中的扩散-对流模型计算得到。
[0084]
本实施例可以通过比较自由氯离子浓度，判别海底隧道保护层位置处的最危险点；通过比较扩散模型和扩散-对流模型中海底隧道最危险点处自由氯离子浓度达到临界
自由氯离子浓度cr的最短时间，来确定海底隧道的耐久寿命t1。
[0085]
实施例二
[0086]
在实施例一的基础上，本技术实施例二提供了实施例一中基于扩散-对流模型的海底混凝土隧道耐久寿命预测方法在舟山沈家门海底隧道中的应用情况：
[0087]
本实例以舟山沈家门海底隧道进行算例分析，该隧道水头压力15m，环境自由氯离子浓度为0.005，混凝土初始饱和度为0.70，饱和渗透系数为1.29e-12，氯离子扩散系数为1.69e-12，保护层厚度为0.05m，临界氯离子浓度为0.1。
[0088]
图1-1至图1-4为根据实施例1提出的非饱和扩散-对流模型计算得到的海底隧道管段内不同时间节点的氯离子浓度分布云图。顶板与侧墙相交的腋角拐点部位氯离子浓度增长最为明显，因此将该点作为危险点。
[0089]
图2为通过改变隧道外壁的水头压力取值，根据darcy方程改变隧道外壁和内部的压力势
▽
ψ
p
，根据实施例1的步骤1和步骤2分别计算出危险点处氯离子浓度随时间的变化规律，根据步骤3确定该浓度达到临界氯离子浓度的时间作为海底隧道的耐久寿命t1。
[0090]
图3为通过改变隧道混凝土的初始饱和度取值，根据richards方程改变隧道外壁和内部的压力势
▽
ψm，根据实施例1的步骤1和步骤2分别计算出危险点处氯离子浓度随时间的变化规律，根据步骤3确定该浓度达到临界氯离子浓度的时间作为海底隧道的耐久寿命t1。
[0091]
图4为通过改变隧道外壁的环境自由氯离子浓度取值，根据fick扩散定律改变隧道的扩散通量jd，根据实施例1的步骤1和步骤2分别计算出危险点处氯离子浓度随时间的变化规律，根据步骤3确定该浓度达到临界氯离子浓度的时间作为海底隧道的耐久寿命t1。
[0092]
图5为分别采用扩散模型、饱和扩散-对流模型和非饱和扩散-对流模型，根据实施例1的步骤1和步骤2分别计算出危险点处氯离子浓度随时间的变化规律，根据步骤3确定只考虑氯离子浓度差引起的扩散模型计算得到的耐久寿命为247年，按饱和混凝土的扩散-对流模型计算得到的耐久寿命为225年，按非饱和混凝土扩散-对流模型计算得到的耐久寿命为133年，故最终预测的隧道耐久寿命t1为133年。
[0093]
本实施例根据海底隧道内外壁存在压力差的服役特点，以及高性能混凝土的非饱和性，建立了海底混凝土隧道氯离子扩散-对流运移模型和耐久寿命预测模型，按照扩散-对流模型预测得到的隧道耐久寿命均小于扩散模型，说明只按扩散模型进行耐久寿命预测可能偏于不安全。两种氯离子扩散-对流模型中，考虑了混凝土初始非饱和状态的预测寿命要低于饱和扩散-对流模型的预测寿命，说明毛细吸力对氯离子运动的驱动作用比仅考虑压力驱动的作用更为明显。因此建议采用非饱和混凝土的扩散-对流模型进行海底隧道耐久寿命预测，可以为海底隧道工程提供准确安全的耐久寿命预测。