一种考虑空间依赖性与异质性的地表温度预测方法

1.本发明属于热岛效应领域，一种考虑空间依赖性与异质性的地表温度预测方法。


背景技术：

2.城市热岛效应，即市区城市温度或地表温度明显高于郊区的现象。热岛效应在改变局部地域气候的同时，并严重威胁着城市居民的生命安全。预计到2100年，城市平均气温可能上升4℃，与《巴黎协定》中的规定全球气温上升限制(不超过1.5℃)相去甚远，逼迫我们不得不立即、迅速、大规模地采取降温措施。因而，如何更全面的分析热岛形成机理，高精度的预测温度空间分布与强度至关重要。
3.tober在1970年提出的地理学第一定律指出：“任何空间事物与其他事物都是相关的，且距离越近空间事物表现越相似”，称为空间依赖性。地表温度作为一种空间数据，其往往具有空间依赖性。空间自回归模型被用来解决空间依赖性，但它依旧是一种全局回归模型，未考虑地表温度的局部特征。各个区域的地表温度由于土地利用情况、建设强度、建筑布局等因素具有不同的强度，导致不同区域的热岛对政府统一制定实施的调控政策具有不同的反应，即宏观改善政策对热岛的影响呈现出异质性。但是，这并不意味着每个区域的热岛对改善政策的反应都不一样，比较接近事实的应该是温度水平相当的区域对同一缓解措施的反应趋于一致。空间分位数回归实现了在捕捉地表温度空间依赖性的同时挖掘各影响因素对地表温度的异质性影响。


技术实现要素：

4.本发明的目的在于克服现有技术的不足，提供一种考虑空间依赖性与异质性的地表温度预测方法。
5.为实现上述目的，本发明的技术方案是：一种考虑空间依赖性与异质性的地表温度预测方法，包括以下步骤：
6.s1：采集建立回归关系需要的城市要素数据及landsat8遥感影像数据；
7.s2：对遥感影像采用大气校正法进行温度反演，获得城市地表温度数据；
8.s3：利用arcgis区域统计工具统计各分析单元的地表温度以及影响热岛效应的因素；
9.s4：检验各影响因素的显著性及多重共线性，保证参与建模的影响因素显著且不存在多重共线性；
10.s5：使用moran’s i判断地表温度的空间自相关性；若存在空间自相关，则进行下面步骤，若不存在则终止计算；
11.s6：当分析单元数量足够大使得误差的空间自相关性不显著时，直接建立空间滞后模型；若数量不足，则需保证在lagrange multiplier检验与robust lagrange multiplier检验下空间滞后模型优于空间误差模型，而后建立空间滞后模型；
12.s7：建立空间分位数模型。
13.2.根据权利要求1所述的一种考虑空间依赖性与异质性的地表温度预测方法，其特征在于，在所述步骤s2中，大气校正法的具体步骤为：
14.基于所述的landsat8遥感影像，辐射定标获得第10波段的大气顶层辐射亮度；
15.计算归一化植被指数，基于所述的归一化植被指数计算植被覆盖度，基于所述的植被覆盖度计算地表比辐射率；
16.基于所述的第10波段的大气顶层辐射亮度计算同为温度为t的黑体在热红外波段的辐射亮度，基于所述辐射亮度计算得到地表温度数据。
17.3.根据权利要求1所述的一种考虑空间依赖性与异质性的地表温度预测方法，其特征在于，在所述步骤s6中，空间滞后模型的计算公式下述：
18.y＝ρwy+βx+ε
19.式中y为地表温度，w为空间权重矩阵，x为影响因素。
20.4.根据权利要求1所述的一种考虑空间依赖性与异质性的地表温度预测方法，其特征在于，在所述步骤s7中，所述的空间分位数模型下述公式
21.y＝ρ(τ)wy+β(τ)x+ε(τ)
22.式中y为地表温度，w为空间权重矩阵，x为影响因素，τ为分位数，取值为0～1。式中未知参数有两种求解方式：
23.第一种是工具变量分位数回归(ivqr)。其求解思路为将在普通最小二乘回归中wy的估计值作为wy的工具变量，普通最小二乘回归是依据一组工具变量z(x和wx)完成的，然后将该工具变量用于y-ρw对x和进行的一系列的分位数回归。需要注意在这一系列的分位数回归中前后使用的分位数τ是相同的。对于未知参数ρ，它的估计值就是的回归系数，接近于0。接下来在计算出后，通过y-ρw对x进行分位数则可以计算得到β的估计值。当工具变量选择合适时，是近似为0的。
24.第二种是两阶段分位数回归(2sqr)。其计算步骤下述
25.wy＝β
*
(τ)x+γ
*
(τ)wx+ε
*
(τ)
[0026][0027][0028]
在第一阶段，基于空间外生变量wx与x对空间滞后内生变量wy实行分位数，而后基于该回归系数计算wy的预测值第二阶段，使用预测值替代wy，基于空间滞后模型再次使用分位数回归，获得当前分位数下最终所需系数ρ(τ)与β(τ)，对每个分位数重复上述两个阶段，获得所有分位数时的回归系数。
[0029]
有益效果：
[0030]
本发明的有益效果在于：
[0031]
1)采用空间分位数回归模型建立影响因素与地表温度之间的影响关系，既考虑了地表温度的空间依赖特征，还抓住了各影响因素对地表温度的异质性影响；
[0032]
2)模型在预测地表温度时精度更高。
[0033]
3)为制定差异化的区域方案和分类分级减缓措施提供理论支撑。
附图说明
[0034]
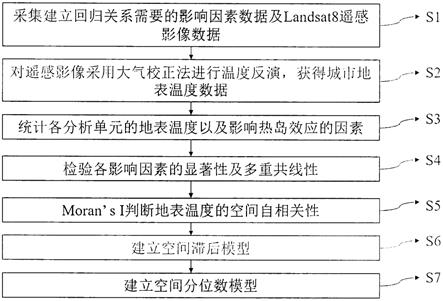
图1是本发明中考虑空间依赖性与异质性的地表温度预测方法的流程图。
具体实施方式
[0035]
下面通过具体实施例1和附图对本发明作进一步的说明。
[0036]
实施例1
[0037]
参照图1，本实施例提供了一种考虑空间依赖性与异质性的地表温度预测方法，包括步骤：
[0038]
s1：采集建立回归关系需要的城市要素数据及landsat8遥感影像数据；
[0039]
s2：对遥感影像采用大气校正法进行温度反演，获得城市地表温度数据；
[0040]
s3：利用arcgis区域统计工具统计各分析单元的地表温度以及影响热岛效应的因素；
[0041]
s4：检验各影响因素的显著性及多重共线性，保证参与建模的影响因素显著且不存在多重共线性；
[0042]
s5：使用moran’s i判断地表温度的空间自相关性；若存在空间自相关，则进行下面步骤，若不存在则终止计算；
[0043]
s6：当分析单元数量足够大使得误差的空间自相关性不显著时，直接建立空间滞后模型；若数量不足，则需保证在lagrange multiplier检验与robust lagrange multiplier检验下空间滞后模型优于空间误差模型，而后建立空间滞后模型；
[0044]
s7：建立空间分位数模型。
[0045]
具体地：
[0046]
在本实施案例中，以城市a2017年7月10日热岛效应为例，影响因素以下垫面因素包括草地比例(gp)、林地比例(tp)、水体比例(wp)、除建筑物外的不透水表面比例(isap)，建筑物因素包括建筑物占地面积(ba)、建筑物立面面积(bsa)、建筑物高度(bh)及天空视域因子(svf)为例。土地利用数据采集自宫鹏团队的2017年10m空间分辨率的土地利用数据，建筑物数据采集自百度地图，时间为2017年第四季度，遥感影像为2017年7月10日的landsat 8卫星数据。
[0047]
步骤s2中，大气校正法的具体步骤为：
[0048]
步骤s201：根据landsat8遥感影像，辐射定标获得第10波段的大气顶层辐射亮度.
[0049]
具体的，根据bi(ti)＝ε
ibi
(ts)τi+(1-εi)r
↓
τi+r
↑
计算得到第10波段的大气顶层辐射亮度，式中，i为第i波段，bi为普朗克函数，bi(ti)为大气顶层辐射亮度，bi(ts)为温度为ts(k)的黑体在传感器上接收到的辐射亮度，εi为地物的比辐射率或称为发射率，τi为第i波段的大气透过率，r
↓
为大气下行辐射，r
↑
为大气上行辐射。
[0050]
步骤s202：计算归一化植被指数，基于所述的归一化植被指数计算植被覆盖度，基于所述的植被覆盖度计算地表比辐射率；
[0051]
根据下式计算归一化植被指数ndvi
[0052][0053]
式中nir、r分别为近红外波段与红光波段像元值，对应landsat 8第5、4波段。
[0054]
根据下式计算植被覆盖度：
[0055][0056]
式中pv为植被覆盖度，ndvi表示上式中计算得到的ndvi值，即归一化植被指数，ndvi
soil
与ndvi
veg
分别表示裸土的像元的ndvi值与纯植被覆盖的ndvi值，分别取值为0.05与0.70。
[0057]
根据下式计算地表比辐射率
[0058]
ε＝0.004pv+0.986
[0059]
其中pv为上式中计算得到的植被覆盖度，ε为地表比辐射率。
[0060]
步骤s203：基于所述的第10波段的大气顶层辐射亮度计算同为温度为t的黑体在热红外波段的辐射亮度，基于所述辐射亮度计算得到地表温度数据。
[0061]
根据下式计算同为温度为t的黑体在热红外波段的辐射亮度
[0062][0063]
式中b(t)为上文中已求解的band10大气顶层辐射亮度；大气透过率τ、大气下行辐射r
↑
与大气上行辐射r
↓
为大气剖面信息，可在nasa发布的官方网站根据影像成像时间与中心经纬度(http：//atmcorr.gsfc.nasa.gov)查询。本实例中τ＝0.84，r
↑
＝1.39w/m2/sr/um，r
↓
＝2.38w/m2/sr/um。
[0064]
根据下式计算地表温度ts，
[0065][0066]
其中k1与k2可在头文件中获取，本实例中band10的k1＝774.8853w/m2/sr/μm，k2＝1321.0789w/m2/sr/μm，b(ts)为上式中计算得到的黑体在热红外波段的辐射亮度。
[0067]
步骤s4中，建筑物高度在本实例中未通过显著性检验，遂剔除该因素。
[0068]
步骤s5中，使用moran’s i判断街区地表温度的空间自相关性；本实例中城市a地表温度的moran
′
s i为0.496，表明地表温度是空间自相关的。
[0069]
步骤s6中，本实例中空间滞后模型优于空间误差模型，根据下式建立空间滞后模型
[0070]
y＝ρwy+βx+ε
[0071]
式中β和ρ是未知参数，w为空间权重矩阵，x与y分别为解释变量与被解释变量地表温度。具体至本实例空间滞后模型公式为：
[0072]
lst＝ρwlst+β
wp
wp+β
gp
gp+β
tp
tp+β
isap
isap+β
ba
ba+β
sa
sa+β
svf
svf+β0+ε
[0073]
式中β
wp
、β
gp
、β
tp
、β
isap
、β
ba
、β
sa
与β
svf
对应wp、gp、tp、isap、ba、sa与svf的回归系数，β0表示截距，ρ为空间依赖项的回归系数，表征空间依赖的能力，以上均为待估计系数。lst为街区地表温度，ε为服从零均值同方差正态分布的随机误差。w为空间权重矩阵，本实例中选用一阶queen邻接矩阵。
[0074]
根据下式建立空间分位数模型
[0075]
y＝ρ(τ)wy+β(τ)x+ε(τ)
[0076]
式中τ为分位数，取值于0～1之间。
[0077]
具体至本实例空间分位数模型公式为：
[0078]
lst＝ρ(τ)wlst+β
wp
(τ)wp+β
gp
(τ)gp+β
tp
(τ)tp+β
isap
(τ)isap+β
ba
(τ)ba+β
sa
(τ)sa+β
svf
(τ)svf+β0(τ)+ε(τ)
[0079]
式中ρ(τ)、β
wp
(τ)、β
gp
(τ)、β
tp
(τ)、β
isap
(τ)、β
ba
(τ)、β
sa
(τ)与β
svf
(τ)为各分位数下空间依赖项与wp、gp、tp、isap、ba、sa与svf的回归系数。
[0080]
优选的，2sqr在估计时拥有更高的计算效率，本实例中使用2sqr估计sqr模型。本实例中以0.1～0.9分位数且间隔0.1为例，空间分位数回归结果下图所示
[0081]
各影响因素的2sqr结果(0.1-0.5分位数)
[0082][0083]
注：***.**和*分别表示0.01、0.05和0.1水平的显著性。括号中的数字表示bootstrap法迭代500次获得的bootstrap标准误差。
[0084]
将上述回归结果应用至研究区域的附近区域b评估模型精度，空间分位数模型的平均绝对误差为0.0578，较空间滞后模型的平均绝对误差(0.0655)小。空间分位数模型的归一化均方根误差为13％，空间滞后模型的归一化均方根误差为13％。误差越小，表明精度越高。因而，相较于空间滞后模型，空间分位数模型预测精度更高，被认为是一种拥有更高精度的地表温度预测方法。
[0085]
本发明的有益效果在于：
[0086]
1)采用空间分位数回归模型建立影响因素与地表温度之间的影响关系，既考虑了地表温度的空间依赖特征，还抓住了各影响因素对地表温度的异质性影响；
[0087]
2)模型在预测地表温度时精度更高。
[0088]
3)为制定差异化的区域方案和分类分级减缓措施提供理论支撑。