基于量子随机游走和离散小波变换的鲁棒图像水印方法

1.本发明涉及信息安全领域，具体是水印安全技术，尤其涉及基于量子随机游走和离散小波变换的鲁棒图像水印方法。


背景技术：

2.如今，数据信息的存储和安全传输是面临的一个重要挑战。密码学的出现为信息加密提供了便捷，但是加密算法一方面在受到攻击和破解后就没办法保护信息安全，另一方面也没有利用到信息本身的信号属性，于是信息隐藏技术出现了。信息隐藏也就是将要传递的秘密信息隐藏在一些传播载体中。秘密信息一般用密钥作进一步加密，即使攻击者获得了秘密信息，由于密钥的不确定性也无法将其解密，具有很好的安全效能。与密码学相比，它的优势在于在不影响载体自身价值的同时也进行了秘密信息的安全传输。
3.数字水印作为信息隐藏技术领域一个重要分支。水印即要传输的秘密信息，传播载体包括图像、音频、视频等。数字水印技术将水印嵌入到传播载体中，在不影响传播载体正常价值的同时达到了信息隐秘传播的目的。基于此，利用数字水印，可以实现版权保护、真伪鉴定、隐蔽通信等。与密码学相比，水印技术完全发挥了载体与水印本身的信号属性，且在传输过程中具有不可感知性，进一步增强了秘密信息的安全性。
4.水印算法有多种分类方法，根据秘密信息嵌入区域的不同，可分为两大类：基于空间域(即空域)的算法和基于频域的算法。空域算法通过将水印信息直接嵌入到载体图像的像素值中达到信息隐藏，计算复杂度低，但是水印信息容易受到各种攻击手段的影响。频域算法是将载体图像转化到变换域后进行的水印嵌入，虽然增大了计算复杂度，但是安全性得到了很大保证。在一些安全性为主的领域中得到了广泛的应用。其中离散小波变换(dwt)以其良好的时空特征属性在频域数字水印中获得了普遍的使用。
5.针对水印算法的性能，可以从不可见性(即不可感知性)和鲁棒性两个方面进行评价。不可见性是衡量载体图像与嵌入图像之间的区别。即，要查看的原始图像和带水印的图像之间有没有差异。鲁棒性是衡量水印图像抵抗各种信号处理技术或者攻击手段的能力。为了提高水印的鲁棒性和不可见性，结合各种数学变换，人们提出了多种混合水印方案。
6.但是现有的水印算法都存在一个问题，即鲁棒性与不可见性不能同时实现，在满足鲁棒性的同时，就必须降低嵌入量保证不可见性。本文拟提出一种方法在保证水印不可见性的同时也可以提高其鲁棒性。
7.水印技术面临的另一个安全问题是使未经授权的人无法读取到水印信息，即在嵌入水印之前对水印图像进行预置乱处理，从而进一步提高方案的安全性。一般来说，诸如arnold变换和混沌加密之类的加密技术用于处理这个问题。但是这些方法的解密的难度较低。因此，有必要提出一种方法来使水印图像更加安全。


技术实现要素：

8.在本发明中，为了提高鲁棒性，选择在频域嵌入水印。离散小波变换(dwt)的优势
是其拥有较好的离散性与空间局部性；离散余弦变换(dct)可以将图像中的重要信息压缩，并集中分步在系数矩阵的左上方。svd系数提供了高鲁棒性、视觉质量和数据有效载荷。因此，本发明将基于这三种水印处理技术，在其混合变换域中完成了水印的嵌入。具体来说，将二级离散小波变换(2-dwt)应用到载体图像上，在其高频系数hh2中完成的水印嵌入，以确保水印的鲁棒性并保持载体图像更好的视觉质量。在对载体图像进行2-dwt后，对其进行分块，对每一个块作dct操作，进一步将图像的主要能量进行了提取。为了尽可能的不影响视觉质量，本发明在交流系数中进行了水印的嵌入，是通过对其进行奇异值分解(svd)，嵌入到该区块的奇异值中实现的。综合离散小波变换(dwt)良好的时空特性、离散余弦变换(dct)的能量紧致性和奇异分解的抗噪性，该水印方案具有较强的鲁棒性和不可见性。
9.量子游走(qrw)是一种对初始条件和参数敏感的数学模型，同时从量子游走中提取数据是一个非线性行为的概率过程，具有稳定性和非周期性的特点，正是由于它的密钥设置具有无数种状态，可以将其应用在抗攻击方面。因此可以将量子游走模型应用到水印图像的加密过程中。本发明提出采用量子随机游走系统对水印图像进行置乱，使水印图像更加安全。
10.本发明是通过以下技术方案实现的：一种基于量子随机游走和离散小波变换的鲁棒图像水印方法，其方法包括以下内容：
11.步骤1：水印图像的预加密。
12.步骤1.1：zigzag置乱水印图像并重构为一维序列。
13.步骤1.2：运用量子随机游走系统生成的随机序列进一步置乱一维序列并反重构为系数矩阵。
14.步骤1.3：利用arnold变换进加扰得到的系数矩阵，得到加密的水印图像。
15.步骤2：将水印图像嵌入到载体图像中。
16.步骤2.1：对步骤1中得到的加密水印图像进行8*8分块，然后对每个块作dct操作，得到大小为8*8的系数矩阵。
17.步骤2.2：将svd应用到每个系数矩阵得到对角矩阵和特征向量。运用量子随机游走系统生成的随机序列对特征向量进行加密。
18.步骤2.3：对载体图像先后进行2级离散小波变换，对高频子带进行16*16分块，然后对每个分块作dct处理，对每个分块的右下角区域(8*8)作svd得到对角矩阵和特征向量。运用量子随机游走系统生成的随机序列对对角矩阵进行加密。
19.步骤2.4：将水印图像的奇异值嵌入到载体图像的奇异值当中。
20.步骤2.5：对载体图像进行逆svd和逆dct运算。
21.步骤2.6：将得到的系数矩阵作为载体图像的高频信息做2级逆dwt，得到载有水印信息的图像，即载密图像。
22.步骤3：从载密图像中提取水印图像。
23.步骤3.1：通过量子随机游走系统生成的随机序列提取出原始的水印图像的特征向量和载体图像的对角矩阵。
24.步骤3.2：通过应用2-dwt将载密图像进行分解，对高频子带进行16*16分块，然后对每个分块作dct操作，并对每个分块的交流分量区域作svd。
25.步骤3.3：从载密图像的对角矩阵中提取水印图像的对角矩阵，联合特征向量先后
进行逆svd、逆dct运算，得到预加密时的水印图像。
26.步骤3.4：对得到的预加密水印图像进行反arnold变换并重构为一维序列，然后对一维序列进行反置乱并进行反重构，对得到的系数矩阵作反zigzag置乱得到最终的原始水印图像。
附图说明
27.通过结合附图对本发明示例性实施例进行更详细的描述，本发明的上述以及其它目的、特征、优势将会更加明显。
28.本发明提出的算法总共分为三步：预加密算法、水印嵌入和水印提取算法。
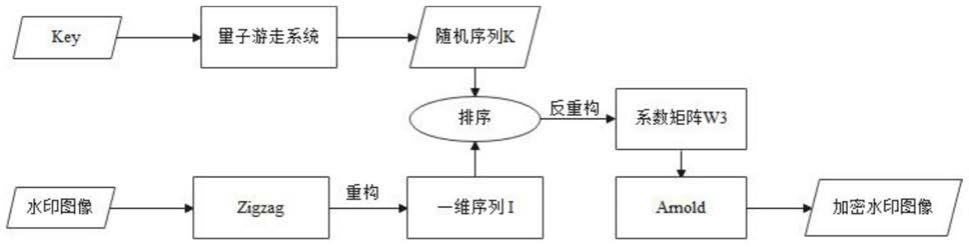
29.图1示出了本发明的基于qrw系统的预加密过程。
30.图2示出了基于离散小波变换的水印嵌入过程。
31.图3示出了对应的水印提取步骤流程图。
具体实施方式
32.下面将参照附图更详细的描述本发明，使本发明的目的、技术方案以及优点更加清楚明白。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
33.本发明将m
×
n的载体图像用i表示，m
×
n的水印图像用w表示。其中m和n为载体图像的长和宽，m和n为水印图像的长和宽。
34.参考图1，如图1所示的是本发明的基于qrw系统的预加密过程。
35.将x个结点环上双粒子qrw系统的初始参数作为密钥key。
36.在整个过程中，首先通过预加密算法e1将大小为m
×
n的水印图像w作置乱加密：w
′
＝e1(w,key)。目的是为了保护原始水印信息，即使水印信息被非法提取后，原始数据也不会直接暴露给对手。其中w
′
为置乱后的水印图像。
37.下面结合图1详细说明根据本发明的基于qrw系统的预加密过程的具体步骤：
38.步骤一：对水印图像w使用zigzag置乱，得到系数矩阵w2。
39.步骤二：将系数矩阵w2重构为一维序列l。
40.步骤三：基于密钥key运行量子随机游走系统生成随机序列k＝{k1,k2,
…
,km×n}。其中k1，k2…
为组成随机序列k的具体数值。
41.步骤四：通过对随机序列k进行排序获得相应的索引序列s1。通过如下公式得到置乱序列l
′
：
42.l
′
(i)＝l(s1(i))
43.其中0＜i＜＜m
×
n，l(s1(i))是序列l的第s1(i)个元素，l
′
(i)和s1(i)分别是序列l
′
和s1的第i个元素。
44.步骤五：对序列l
′
进行反重构，得到大小为m
×
n的系数矩阵w3。
45.步骤六：利用arnold变换进一步加扰w3得到加密的水印图像w
′
。
46.参考图2，如图2所示的是本发明的水印嵌入过程。
47.通过水印嵌入算法e2，将图像w
′
嵌入到载体图像i中：[iw,ewuv,eis]＝e2(w
′
,i,key)。其中iw为载密图像，ewuv和eis分别是水印图像w
′
的特征向量矩阵和载体图像i的奇
异值矩阵的加密系数矩阵。
[0048]
下面结合图2详细说明根据本发明的水印嵌入的具体步骤：
[0049]
步骤一：输入密钥key，运行量子随机游走系统生成随机序列z，使得z＝{z1,z2,z3,...,z2×m×n}。其中z1，z2…
为组成随机序列z的具体数值。
[0050]
步骤二：对序列z排序，得到对应的索引序列s2。
[0051]
步骤四：对w
′
进行8*8分块，然后对每个块作dct操作，得到大小为8*8的系数矩阵wdj，其中j∈[1,(m
×
n)/82]。
[0052]
步骤五：将svd应用到每个wdj系数矩阵，得到大小为8*8的对角矩阵wsj和特征向量wuj、wvj。
[0053]
步骤六：将wuj和wvj共同表示为wuv并对其加密，如以下公式所示：
[0054]
ewuv(k)＝wuv(s2(k))
[0055]
其中0＜k＜＜2
×m×
n。wuv(s2(k))表示wuv的第s2(k)个元素，ewuv(k)和s2(k)分别为ewuv和s2的第k个元素。
[0056]
步骤八：对载体图像i应用n级离散小波变换，获得以下四个子带lln、lhn、hln、hhn。其中lln、lhn、hln、hhn分别为图像经过变换后的低频信息、水平高频信息、垂直高频信息和对角高频信息,hhn被用于嵌入水印。n为变换的级数，在该方法中，通过如下公式将载体图像分解为2层，即n＝2层。
[0057]
[ll2,lh2,hl2,hh2]＝dwt(i)
[0058]
步骤九：对子带hh2进行16*16分块，然后对每个分块作dct处理，得到大小为16*16的系数矩阵idj，其中
[0059]
步骤十：对矩阵idj的右下角区域(8*8)作svd，得到大小为8*8的奇异值对角矩阵isj和相应的特征向量iuj、ivj。
[0060]
步骤十一：将isj共同表示为is并作加密处理，公式如下所示：
[0061]
eis(k)＝is(s2(k))
[0062]
其中is(s2(k))表示is的第s2(k)个元素，eis(k)和s2(k)分别为eis和s2的第k个元素。
[0063]
步骤十二：通过如下公式将wsj嵌入到isj中：
[0064]
esj＝isj+(α
×
wsj)
[0065]
其中α为比例系数因子，
[0066]
步骤十三：通过以下公式对esj进行逆svd，得到大小为8*8的系数矩阵iesj：
[0067]
iesj＝iuj×
esj×
ivj[0068]
其中iuj、ivj分别为对应的特征向量。
[0069]
步骤十四：将每个idj的右下角区域(8*8)替换成iesj，得到大小为16*16的系数矩阵eidj。然后，对eidj进行逆dct运算，并合并得到的每个区块，得到包含水印相关数据的
hh
21
。
[0070]
步骤十五：使用修改后的系数矩阵hh
21
作2级逆dwt，得到载有水印信息的图像iw，公式如下所示。
[0071]iw
＝2-idwt(ll2,lh2,hl2,hh
21
)
[0072]
参考图3，如图3所示的是本发明的水印提取过程。
[0073]
通过提取算法d从载密图像iw中提取原始水印图像w：w＝d(iw,ewuv,eis,key)，其中key为密钥，d为水印提取算法。ewuv和eis分别为wuv和is的加密矩阵。
[0074]
下面结合图3详细说明根据本发明的水印提取的具体步骤：
[0075]
步骤一：基于密钥key运行量子随机游走系统生成随机序列z和k，使得z＝{z1,z2,z3,
…
,z2×m×n},k＝{k1,k2,
…
,km×n}。
[0076]
步骤二：对序列k和z排序，得到相应的索引序列s1、s2。
[0077]
步骤三：计算公式如下所示得到wuv和is，并提取出矩阵wuj、wvj和isj。
[0078]
wuv(s2(q))＝ewuv(q)
[0079]
is(s2(p))＝eis(p)
[0080]
其中0＜q＜＜2
×m×
n，eis(p)为eis第p个元素。wuv(s2(q))为wuv的第s2(q)个元素，is(s2(p))表示is的第s2(p)个元素，ewuv(q)和s2(q)分别为ewuv和s2的第q个元素。
[0081]
步骤五：通过应用2-dwt将载密图像iw分解成子带；
[0082]
(ll2,lh2,hl2,hh
21
)＝dwt(iw)
[0083]
步骤六：对子带hh
21
先进行16*16分块，然后对每个分块作dct操作，得到大小为16*16的系数矩阵eidj，其中
[0084]
步骤七：对矩阵eidj的交流分量区域作svd，得到大小为8*8的对角矩阵esj。
[0085]
步骤八：根据如下公式得到大小为8*8的水印图像的奇异值对角矩阵wsj：
[0086]
wsj＝(es
j-isj)/α
[0087]
其中是α比例系数因子，且
[0088]
步骤九：对wsj进行逆svd，如以下公式所示：
[0089]
wdj＝wuj×
wsj×
wvj[0090]
其中wuj、wvj为对应的特征向量。
[0091]
步骤十：对wdj应用逆dct运算，得到w
′
。
[0092]
步骤十二：对w
′
进行反arnold变换得到系数矩阵w3，并重构为一维序列l
′
。
[0093]
步骤十三：通过对l
′
进行反置乱得到序列l，公式如下：
[0094]
l(s1(k))＝l
′
(k)
[0095]
其中0＜k＜＜m
×
n，l(s1(k))是序列l的第s1(k)个元素，l
′
(k)和s1(k)分别是序列l
′
和s1的第k个元素。
[0096]
步骤十四：通过对序列l进行反重构得到图像w2。
[0097]
步骤十五：对w2进行反zigzag置乱，最终提取出了大小为m
×
n的原始水印图像w。