一种不确定的数据交互图中挖掘子图的方法及装置

1.本发明涉及数据挖掘领域，尤其是涉及一种不确定图中挖掘(k,θ)-clique的方法及装置。


背景技术：

2.近几年来，全球大数据进入加速发展时期，数据量呈现指数级、爆发式增长，而这些大量数据中不同个体间彼此交互产生的数据以图的形式表现。因此，从一个复杂的网络挖掘子图成为一个重要的课题。同时，团是最为广泛使用的子图模型，其用于在社交网络发现重叠社群，检测社会阶层以及在蛋白质交互作用中识别蛋白质复合体等。因此，如何高效地从图中挖掘子图成为社会各界需要解决的重大挑战。
3.从过去几年看，现有的研究主要侧重于对于确定图的最大团的枚举。但是在现实场景中，由于实验推断链接、不确定的链路连通性以及潜在影响，网络是不确定的。因为不确定性，从不确定图中挖掘子图，比在确定图中挖掘更为困难，也因此吸引了广泛关注，得到了一些实用的模型。在现有的解决方案中，(k,τ)-clique被广泛使用于在不确定图中建模、表示以及组织相互关联的数据，尤其使用于在给定的概率图发现可靠集群、在不确定网络中挖掘凝聚子图。然而，由于(k,τ)-clique的概率由每条边直接影响，导致子图的概率容易受到较大波动。并且在现实场景中，数据之间的关系不总是稳定的，比如说人际关系网络中，人与人之间的关系受到各种因素影响，所以如果使用(k,τ)-clique，会导致挖掘结果的巨大波动性。
4.因此随着大数据时代的到来，尤其是以图形式相互关联的数据爆发式增长，高效稳定的挖掘子图算法显得尤为重要，如果没有高效稳定的算法，这将成为网络分析的主要障碍之一。
5.但是，现有的子图挖掘技术存在子图稳定性差、挖掘过程计算量大的问题。


技术实现要素：

6.为解决现有技术的不足，实现提高不确定图中挖掘子图的稳定性差，降低计算量的目的，本发明采用如下的技术方案：
7.一种不确定的数据交互图中挖掘子图的方法，包括如下步骤：
8.s1，输入不确定图度数限制k、概率临界值θ，不确定图用于表示连接关系不稳定的多个结点之间的关系，度数限制k、概率临界值θ用于获取满足特定限制的子图；
9.s2，对不确定图进行剪枝，大大简化要挖掘的图，从而降低计算过程中的资源耗费；
10.s3，对剪枝后的不确定子图的每个结点u，求出其出现的概率p(u)；
11.s4，对剪枝后的不确定子图中的每个结点u进行遍历，当结点出现的概率p(u)小于概率临界值θ时，将结点u从剪枝后的不确定子图中移除。
12.进一步地，还包括s5，从s4所得的剪枝后的不确定图中找出极大确定图，并求出极
大确定图的所有极大(k,θ)-clique。
13.进一步地，还包括s6，返回s5得到的所有极大(k,θ)-clique。
14.进一步地，s2中的剪枝，采用基于度数的剪枝策略，遍历不确定图中的每个结点，将度数≤k的结点u放入队列q，当q不为时，取出队列q的首元素记为u，遍历结点u在不确定图中的每个邻居结点v，将结点v和结点u之间的边(u,v)从不确定图中删除，更新删除边(u,v)后的v的度数，如果结点v的度数≤k，则将结点v放入队列q，重复此步骤，直到队列q为空，，返回剪枝后的不确定图
15.进一步地，s2中的剪枝，采用基于θ-degree的剪枝策略，获取不确定图概率临界值θ，最大确定图gm，遍历不确定图中的每个结点u，使用动态规划算法维护二维变量yu(h,i)，计算公式如下：
16.yu(0,i)＝0,i∈[1,k]
[0017]yu
(h,0)＝1,h∈[0,du(gm)]
[0018][0019]
其中h和i皆表示结点的度数，i≤h，且当k≤h时计算才有效，gh表示有h条边的图，yu(h,i)表示结点u在gh中的度数大于i的概率，du(gm)表示结点u在最大确定图gm中的度数，p
eh
表示边eh的概率；如果yu(du(gm),k)《θ，则将结点u从不确定图中删除，返回剪枝后的不确定图
[0020]
进一步地，s2中的剪枝，采用基于马尔可夫上界的剪枝策略，获取不确定图度数限制k，概率临界值θ和最大确定图gm，将队列q设置为空集，遍历中的每一个结点u，将每个结点u的马尔可夫上界概率p
+
(u)赋值为表示在不确定图中结点u的度数大于等于k的概率，将结点u放入队列q；当q不为时，取出q队首元素结点u，根据如下公式更新结点u的马尔可夫上界概率p
+
(u)，直到队列q为空：
[0021][0022]
遍历不确定图g中的每个结点u，如果其马尔可夫上界概率p
+
(u)《θ，则将结点u从不确定图中删除，返回剪枝后的不确定图du(gm)表示结点u在最大确定图gm中的度数，e(u,vi)表示节点u和节点vi之间的边，p(e(u,vi))表示边的概率，如此可以减小图的规模。
[0023]
进一步地，s3中基于蒙特卡罗方法的概率计算方法，计算所有结点在不确定图中的概率p(u)，包括如下步骤：
[0024]
s31，输入不确定图度数限制k、概率临界值θ；
[0025]
s32，遍历不确定图的结点u，将每个结点所在的最大k-clique数初始化为0，即uc＝0；
[0026]
s33，首先计算所有样本图中最大k-clique的总数ns，所述样本图，是先根据不确定图得到一组确定图，再从确定图中抽样得到样本图；
[0027]
s34，将样本图定义为集合s，对样本图集合s中的每个实例图g，求出实例图g的最大k-clique，对于最大k-clique，求出其中每个结点u所在的最大k-clique数，得出每个结点出现的最大k团的数量作为uc；
[0028]
s35，对每个结点u求出其对不确定图的概率p(u)，即每个结点u的k-clique频率，计算公式为：
[0029]
p(u)＝uc/ns[0030]
s36，返回概率p(u)≥θ的结点u的集合。
[0031]
进一步地，s34中每个结点出现的最大k团的数量计算公式为：
[0032]
uc＝uc+1。
[0033]
一种不确定的数据交互图中挖掘子图的装置，包括一个或多个处理器，用于实现权利要求1-8中任一项所述的一种不确定的数据交互图中挖掘子图的方法。
[0034]
本发明的优势和有益效果在于：
[0035]
与现有技术相比，本发明充分考虑了现实场景中数据的不稳定性对子图概率造成的波动，提高了子图挖掘的稳定性；同时使用三种剪枝算法，减少计算量，在相同挖掘场景下对比其他挖掘子图的算法大大降低了资源的消耗。
附图说明
[0036]
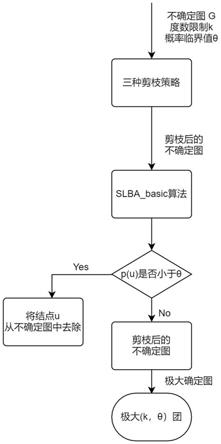
图1是本发明的方法流程图。
[0037]
图2是本发明中不确定图的示意图。
[0038]
图3是本发明中马尔可夫上界剪枝算法示意图。
具体实施方式
[0039]
以下结合附图对本发明的具体实施方式进行详细说明。应当理解的是，此处所描述的具体实施方式仅用于说明和解释本发明，并不用于限制本发明。
[0040]
如图1所示，在社交网络中，采用k-clique表示一个用户社群，通常采用(k,τ)-clique模型，然而在社交网络中每条边的概率变化较大，而(k,τ)-clique的计算方式受到每一条边的影响，所以((k,τ)-clique模型不稳定，因此本发明实施例提供的不确定图中的(k,θ)-clique挖掘方法，包括如下步骤：
[0041]
步骤1，输入不确定图度数限制k，概率临界值θ；
[0042]
具体的，由于两个结点之间的连接是不稳定的，因此表示结点与结点之间关系的图是不确定，所以用不确定图来表示连接关系不稳定的多个结点之间的关系，同时子图挖掘问题是从图中获取一些满足特定限制的子图来解决问题，因此设置度数限制k，概率临界值θ。例如在图2所提供的不确定图的示意图中，有4个结点v1,v2,v3,v4，每条边的概率为0.9。
[0043]
步骤2，对输入不确定图进行剪枝，大大简化要挖掘的图，从而降低计算过程中的资源耗费；
[0044]
在本步骤中，采用三种方法对不确定图进行剪枝。
[0045]
方法一，是基于度数的剪枝策略，对输入不确定图进行剪枝，包括以下过程：遍历不确定图中的每个结点，将度数≤k的结点u放入队列q；当q不为时，取出队列q的首元素记为u，遍历结点u在不确定图中的每个邻居结点v，将结点v和结点u之间的边(u,v)从不确定图中删除，更新删除所述边(u,v)后的v的度数，如果结点v的度数≤k，则将结点v放入队列q，重复此步骤，直到队列q为空。
[0046]
例如在图2所提供的不确定图的示意图中，有4个结点v1,v2,v3,v4，若设置k＝1，节点度数k是指和该节点相关联的边的条数，又称关联度，则v2首先被放入队列q，删除v2的邻边，剩余的节点中没有度数≤1的结点，则剩余的结点v1,v3,v4构成的图为剪枝后的图。
[0047]
方法二，是基于θ-degree的剪枝策略对所述输入不确定图进行剪枝，包括以下过程：获取不确定图概率临界值θ，最大确定图gm；遍历不确定图中的每个结点u，使用动态规划算法维护二维变量yu(h,i)，计算公式如下：
[0048]yu
(0,i)＝0,i∈[1,k]
[0049]yu
(h,0)＝1,h∈[0,du(gm)]
[0050][0051]
其中h和i皆表示结点的度数，i≤h，且当k≤h时计算才有效，gh表示有h条边的图，yu(h,i)表示结点u在gh中的度数大于i的概率，du(gm)表示结点u在最大确定图gm中的度数，p
eh
表示边eh的概率；如果yu(du(gm),k)《θ，则将结点u从不确定图中删除。
[0052]
方法三，是基于马尔可夫上界的剪枝策略，对输入不确定图进行剪枝，包括以下过程：获取不确定图正整数k，概率临界值θ和最大确定图gm；将队列q设置为空集，遍历中的每一个结点u，将每个结点u的马尔可夫上界概率p
+
(u)赋值为表示在不确定图中结点u的度数大于等于k的概率，将结点u放入队列q；当q不为时，取出q队首元素结点u，根据如下公式更新结点u的马尔可夫上界概率p
+
(u)，直到队列q为空：
[0053][0054]
遍历不确定图g中的每个结点u，如果其马尔可夫上界概率p
+
(u)《θ，则将结点u从不确定图中删除；返回剪枝后的不确定图e(u,vi)表示两个节点之间的边，p(e(u,vi))表示边的概率。
[0055]
例如在图3中假设k＝3，初始化各个结点的马尔可夫概率为p
+
(v1)＝p
+
(v3)＝0.729，p
+
(v2)＝p
+
(v4)＝0.081，因此可以得到因此p
+
(v1)从0.729被更新为0.297，如果p
+
(u)的概率小于θ，则将结点u从中删除，假设θ＝0.3，则可以将结点v1从图中删除，如此可以减小图的规模。
[0056]
步骤3，对输入不确定图的每个结点u，求出其出现的概率p(u)；
[0057]
本步骤通过利用蒙特卡罗方法计算所有结点在不确定图中的概率p(u)。具体的，采用sampling-based算法(以下简称slba-basic)，对输入不确定图的每个结点u，求其出现的概率，slba-basic是一个基于蒙特卡罗方法的概率计算方法，其计算过程如下：
[0058]
输入步骤1不确定图度数限制k，概率临界值θ；遍历不确定图的结点u，将每个结点所在的最大k-clique数初始化为0，即uc＝0；首先计算所有样本图中最大k-clique的总数ns；将样本图定义为集合s；对样本图集合s中的每个实例图g，求出实例图g的最大k-clique，对于最大k-clique，求出其中每个结点u所在的最大k-clique数，计算公式为：
[0059]
uc＝uc+1
[0060]
由此得出每个结点出现的最大k团的数量uc；
[0061]
对于一个有n个节点的不确定图，由于每个节点可能存在也可能不存在，则会有2n个确定图，即对每个结点确定的取存在或不存在，又如计算量大，本发明从确定图中抽样，得到样本图，样本图组合成一个样本图集合，实例图即样本图。例如：有不确定图由{a,b}表示，则由该不确定图得到的确定图可以是{a}，也可以是{b}，可以是空的图(即a和b都不在)，可以是{a,b}，需要计算出所有的确定图需要算出4个，过于复杂，便挑出一部分，随机选择两个。
[0062]
对每个结点u求出其对步骤1输入不确定图的概率p(u)，即每个结点u的k-clique频率，计算公式为：
[0063]
p(u)＝uc/ns[0064]
返回概率p(u)≥θ的结点u的集合。
[0065]
步骤4，对步骤3得到的剪枝后的不确定子图中的每个结点u进行遍历，当结点出现的概率p(u)小于步骤1中的概率临界值θ时，将结点u从剪枝后的不确定子图中移除；
[0066]
步骤5，找出步骤4中所得的剪枝后的不确定图的极大确定图，并求出极大确定图的所有极大(k,θ)-clique；
[0067]
步骤6，返回步骤5中得到的所有极大(k,θ)-clique。
[0068]
挖掘图中的代表团的，(k,θ)-clique模型本身，比现有的(k,τ)-clique更具有稳定性，更具代表性，对于社交网络，通过(k,θ)-clique模型挖掘的子图所表示的社交结点间的关系，也更具代表性。
[0069]
以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明实施例技术方案的范围。