一种基于代价敏感支持向量机的发电企业识别方法

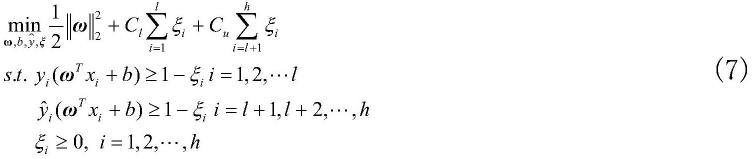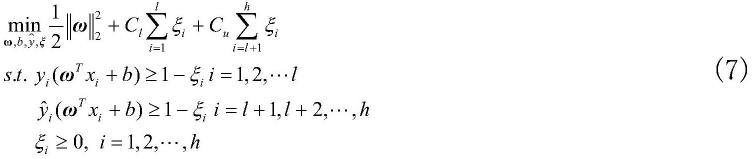
1.本发明属于电力市场主体风险识别方法设计领域，具体涉及一种基于代价敏感支持向量机的发电企业识别方法。


背景技术：

2.在新一轮电改的推进下，我国电力市场化程度不断加强，市场交易不断增加，这使得电力市场在快速发展的同时也伴随着相应的市场风险。
3.目前国内识别发电企业滥用市场力的方法主要有专家决策、构建监管指标体系法等。但随着电力市场的交易规模的扩大以及交易的频次的增加，专家决策的方法已经不能满足实时识别发电企业滥用市场力行为的需求，有必要寻找一种能够使用计算机计算的智能识别方法。此外，监管指标体系中指标的获取均建立在对发电企业的真实情况有一个具体全面了解的前提下，这在实际电力市场中是难以实现的，容易获得的只有报价数据，因此本发明提出了一种基于报价数据的发电企业滥用市场力智能识别方法。
4.发电企业滥用市场力的识别在本质上是一种二分类问题，支持向量机作为一种智能算法，具有准确率高且泛化能力强的特点，在二分类问题上有很强的适用性。但由于发电企业数据中仅有少量数据是有标签数据，使用传统的支持向量机可能会存在过拟合问题。而半监督支持向量机可以利用无标签样本的数据结构信息，很好地解决由于有标签样本较少带来的泛化能力较差的问题，因此采用半监督支持向量机中的直推式支持向量机(transductive supportvector machine,tsvm)，并针对违规数据不平衡的特点选择了代价敏感直推式支持向量机(cost-sensitive transductive support vector ma-chine，ctsvm)。此外，基于tsvm本身需要预置正负类别样本点数目问题，使用k-means方法对无标签数据进行初始标签指派。为了避免半监督支持向量机可能会对样本标签标记错误，采用成对交换标签的方式得到预测标签。在计算复杂度上，tsvm的时间复杂度远高于普通支持向量机，且使用的成对交换标签方式具有准确率高但速度较慢的特点，针对这一问题，使用更为高效的基于定制近邻点算法的变分不等式方法加快求解方法得到判别函数，实现发电企业滥用市场力的实时识别。


技术实现要素：

5.针对上述背景技术中提到的发电企业数据中仅有少量数据是有标签数据以及传统滥用市场力行为识别方法处理交易数据效率低下的问题，本发明提出了一种基于代价敏感支持向量机的发电企业识别方法，克服了现有技术的不足，具有良好的效果。
6.本发明所述一种基于代价敏感支持向量机的发电企业识别方法，包括如下步骤：
7.s1、获得发电企业的申报电量和申报电价数据；
8.s2、构建发电企业的滥用市场力行为识别指标体系，指标包括：发电企业报价数据、各段申报电量份额、各段成交电量份额、各段申报成功比、是否为本段高价、高报价次数；
9.s3、当报价段数较高时，使用主成分分析法对数据进行降维；
10.s4、采取k-means算法对无标签样本进行初始“伪标签”指派，结合半监督支持向量机，采用成对交换标签的方式交换标记错误的标签，得到预测标签；
11.s5、将处理后的滥用市场力数据集代入代价敏感直推式支持向量机，将求解问题转化为变分不等式问题，并使用定制邻近点算法进求解，通过判别函数确定样本标签yi，得到滥用市场力的发电企业。
12.优选地，步骤s1中，获得某一时期中m家发电企业的原始申报数据和和和分别表示第i个发电企业第j段的申报电价和申报电量；例如在三段式报价规则中，
13.优选地，步骤s2中，根据以往滥用市场力行为识别指标的特征描述及特点，并结合电力市场的实际情况，构建完善的滥用市场力行为识别指标体系；
14.发电企业报价数据为指标1，计算公式为：
[0015][0016]
式中：x
1i
表示发电企业的报价数据，分别表示第i个发电企业第j 段的申报电价、申报电量及成交电量，i＝1,2,
…
,m，j＝1,2,
…
n，m为发电企业个数， n为报价段数；
[0017]
各段申报电量份额为指标2，表示该企业在本段报价中拥有的市场力大小，计算公式为：
[0018][0019]
式中：x
2ij
表示第i个企业的第j段申报电量份额；
[0020]
各段成交电量份额为指标3，表示该发电企业竞价成功的电量，体现了利用市场力的可能性大小，计算公式为：
[0021][0022]
式中：x
3ij
表示第i个企业的第j段成交电量份额；
[0023]
各段申报成功比为指标4，反映该企业在本段报价中竞价策略的成败，体现了滥用市场力的可能性大小，计算公式为：
[0024][0025]
式中：x
4ij
表示第i个企业的第j段申报成功比；
[0026]
是否为本段高价为指标5，表示该企业是否愿意冒更大的风险来获取更高的利益，体现了利用市场力的意图大小，计算公式为：
[0027]
[0028]
式中：x
5ij
表示第i个企业在第j段报价中是否为本段高价；
[0029]
高报价次数为指标6，表示该企业滥用市场力的意图大小，计算公式为：
[0030][0031]
式中：x
6i
表示第i个发电企业第j段高报价次数。
[0032]
优选地，步骤s3中，由于发电企业报价数据在报价段数多时维度较高，而支持向量机在数据高维度情形下适用性较差，因此使用主成分分析法pca对高维数据进行降维；
[0033]
优选地，步骤s4中，构造的样本数据包含上述基于报价数据识别指标体系中的指标：发电企业报价数据x
1i
、各段申报电量份额x
2i
、各段成交电量份额x
3i
、各段申报成功比x
4i
、是否为本段高价x
5i
、高报价次数x
6i
以及发电企业滥用市场力标签yi。
[0034]
针对发电企业报价有标签数据较少，以及数据具有极其不平衡的特点，采取了代价敏感直推式支持向量机(ctsvm)。tsvm算法本身需要预置无标签样本中正负类别样本点数目，但由于实际样本中有标签样本数目较少，有标签样本中正负类样本数目不足以代表无标签中正负类样本数目，因此采取k-means算法对无标签样本进行初始“伪标签”指派，然后采用成对交换标签的方式交换标记错误的标签，得到预测标签。
[0035]
在所有样本中，设给定有标签样本集d
l
＝{(x1,y1),(x2,y2),
…
,(x
l
,y
l
)}和无标签样本集du＝{(x
l+1
,y
l+1
),(x
l+2
,y
l+2
),
…
,(x
l+u
,y
l+u
)}。其中l为有标签样本数量，u为无标签样本数量，l+u＝h为总样本数量。yi∈{1,-1}为样本标签，1表示未违规，-1 表示违规。设最优分类界面为ω
t
x+b＝0，ctsvm的目标是为无标签样本集du中样本给出预测标签其中ctsvm的二次规划模型为：
[0036][0037]
式中：ξ为松弛向量，ξi(i＝1,2,
…
,l)对应有标签样本的松弛变量，ξi(i＝l+1,l+2,
…
,h)对应无标签样本的松弛变量。c
l
,cu分别对应有标签样本的惩罚系数和无标签样本的惩罚系数，表示两类样本的重要程度。其中惩罚系数c
l
和 cu定义如下：
[0038][0039]
且满足其中num1、num2分别表示有标签样本中正负样本个数。
[0040]
当样本点线性不可分时，还需要引入核函数，将其转化为线性可分数据进行处理。核函数的一般定义如下：
[0041]
k(xi,xj)＝《φ(xi),φ(xj)》＝φ
t
(xi)
·
φ(xj)
[0042]
其中《.,.》表示内积运算。
[0043]
所述k-ctsvm具体训练步骤如下：
[0044]
1)步骤1：设定c
l
,cu的值，其中cu≤c
l
，使用k-means算法对无标签样本聚成两类，
统计两类样本数目，将数目较少的一类样本标签设成另一类设成得到无标签样本的初始“伪标签”；
[0045]
2)步骤2：使用步骤1中“伪标签”样本和有标签样本一起代入ctsvm中进行训练，寻找一对异号“伪标签”判断对应松弛变量是否满足ξi＞0,ξj＞0,ξi+ξj＞2，若满足条件则交换标签交换完成后重新代入 ctsvm 中进行训练，重复上述过程，直到没有满足上述条件的“伪标签”；
[0046]
3)步骤3：逐渐增大参数cu，cu＝min{2cu,c
l
}，重复步骤2中操作，直到cu≥c
l
，算法结束，输出最后一次训练结果。
[0047]
优选地，步骤s5中，由于tsvm本身存在时间复杂度高的问题，在样本数据量较大时，计算缓慢。并且tsvm采取成对交换标签的方式，这种方式虽然准确率高但速度较慢。为加快求解速度，将其求解问题转化为变分不等式问题，并使用定制邻近点算法对变分不等式问题进行求解，具体步骤如下：
[0048]
步骤1：根据拉格朗日对偶原理将式(7)转化为：
[0049][0050]
设矩阵将式(8)转化为矩阵形式，具体形式如下：
[0051][0052]
式中：c为h
×
1的矩阵，c(i)＝c
l
(i＝1,2,
…
,l)，c(i)＝cu(i＝l+1,l+2,
…
,h)，而e则表示分量全为1的列向量。
[0053]
步骤2：设数据标签向量的零空间矩阵为z，因为y
t
α＝0，则原问题中α可由矩阵z线性表示为α＝zυ。然后原问题就可以转化为线性不等式约束的凸优化问题：
[0054][0055]
步骤3：首先将凸优化问题写成lagrange函数形式：
[0056]
l(υ,λ)＝θ(υ)-λ
t
(aυ-b)
[0057]
然后求其lagrange函数鞍点(υ
*
,λ
*
)相当于求解以下变分不等式问题：
[0058]
θ(υ)-θ(υ
*
)+(ω-ω
*
)
t
f(ω
*
)≥0,ω∈ω
[0059]
式中：
[0060]
步骤4：使用定制邻近点算法求解变分不等式问题。对于给定ωk＝(υk,λk)定制邻近点算法具体表示如下：
[0061]
ωk＝(υk,λk)
[0062][0063]
将(10)式中θ(υ)代入上式得到基于cppa的k-ctsvm迭代算法：
[0064][0065]
式中：p＝[z
t
hz+diag(r)]-1
。当r
·
s≥||a
t
a||时，cppa算法收敛。
[0066]
步骤5：使用判别函数f(x)＝sgn[w
*
x+b
*
]确定样本标签当输出结果为-1时，说明该发电企业滥用市场力。
[0067]
基于cppa的k-ctsvm迭代求解算法具体流程如下：
[0068]
1)设定初始值k＝0，ω0＝(υ0,λ0)，选择满足条件的r,s；
[0069]
2)根据ωk，按照式(11)迭代方式进行迭代，得到和ω
k+1
；
[0070]
3)如果记录υk并转至4，反之k＝k+1转回2；
[0071]
4)通过α＝zυ，计算求得α；
[0072]
5)根据α求得分类超平面参数：
[0073]
6)使用判别函数f(x)＝sgn[w
*
x+b
*
]确定样本标签当输出结果为-1时，说明该发电企业滥用市场力。
[0074]
本发明所述一种基于代价敏感支持向量机的发电企业识别方法，其有益效果在于：本发明能够高效实时地识别电力市场交易中的滥用市场力行为，更好地维护电力市场主体的自身利益、构建公平的市场环境，对贯彻落实市场监管、建立良好市场秩序、保障电力市场健康发展具有重要意义。
具体实施方式
[0075]
实施例1
[0076]
本发明所述一种基于代价敏感支持向量机的发电企业识别方法，包括如下步骤：
[0077]
s1、采用某省电力市场集中竞价中4场三阶段式报价数据作为原始数据和其中和分别表示第i个发电企业第j段的申报电价和申报电量；
[0078]
s2、构建发电企业的滥用市场力行为识别指标体系，指标包括：发电企业报价数据、各段申报电量份额、各段成交电量份额、各段申报成功比、是否为本段高价、高报价次
数；
[0079]
具体地，发电企业报价数据为指标1，计算公式为：
[0080][0081]
式中：x
1i
表示发电企业的报价数据，分别表示第i个发电企业第j 段的申报电价、申报电量及成交电量，i＝1,2,
…
,m，j＝1,2,
…
n，m为发电企业个数， n为报价段数；
[0082]
各段申报电量份额为指标2，计算公式为：
[0083][0084]
式中：x
2ij
表示第i个企业的第j段申报电量份额；
[0085]
各段成交电量份额为指标3，计算公式为：
[0086][0087]
式中：x
3ij
表示第i个企业的第j段成交电量份额；
[0088]
各段申报成功比为指标4，计算公式为：
[0089][0090]
式中：x
4ij
表示第i个企业的第j段申报成功比；
[0091]
是否为本段高价为指标5，计算公式为：
[0092][0093]
式中：x
5ij
表示第i个企业在第j段报价中是否为本段高价；
[0094]
高报价次数为指标6，计算公式为：
[0095][0096]
式中：x
6i
表示第i个发电企业第j段高报价次数。
[0097]
s3、使用主成分分析法对数据进行降维，采取k-means算法对无标签样本进行初始“伪标签”指派，结合半监督支持向量机，采用成对交换标签的方式交换标记错误的标签，得到预测标签，具体步骤见表1；
[0098]
表1 智能识别方法具体步骤
[0099][0100][0101]
s4、将处理后的滥用市场力数据集代入代价敏感直推式支持向量机，将求解问题转化为变分不等式问题，并使用定制邻近点算法进求解，具体步骤见表2，通过判别函数确定样本标签yi，得到滥用市场力的发电企业；
[0102]
表2 基于cppa的k-ctsvm迭代求解算法流程
[0103][0104]
s5、评价指标采用正确率和召回率，正确率、召回率定义如下：
[0105]
正确率为：
[0106]
召回率为：
[0107]
式中：tp,tn,fp,fn定义见表3中所述混淆矩阵。
[0108]
表3 混淆矩阵
[0109][0110]
为体现改进代价敏感直推式支持向量机的发电企业滥用市场力识别效率，通过三个数据集实例与其他智能算法进行了对比：
[0111]
uci数据集测试：
[0112]
使用k-ctsvm以及svm两种算法对uci数据集(iris、wine、glass、haberman) 进行测试。为充分模拟实际电力市场数据，设定测试数据集数量为50个，其中负类样本比例占总样本数的10％，有标签样本占总样本数的20％。uci数据集测试结果见表4。
[0113]
表4 uci数据集测试结果
[0114][0115]
从表4可以看出k-ctsvm在与svm正确率相差不多的情况下，召回率远高于svm。说明k-ctsvm算法比传统svm的拟合效果要好，识别效率更高，因此本发明提出的算法可以有效识别出只占样本小部分的违规样本。
[0116]
电力市场数据测试：
[0117]
使用k-ctsvm、tsvm以及svm三种算法对数据集进行电力市场仿真实验，数据集基于三段式报价、统一出清价格机制进行构造。设定发电企业数量是39 个，经判定给出滥用市场力发电企业5个，未滥用市场力发电企业34个。并选取20％的样本作为有标签样本，其余为无标签样本。
[0118]
使用滥用市场力识别指标体系构造样本集，对样本数据进行pca降维处理，将降维后数据集代入支持向量机(svm)、直推式支持向量机(tsvm)和改进代价敏感直推式支持向量机(k-ctsvm)中进行测试，并使用cppa算法及序列最小优化算法(sequential minimal optimization,smo)计算，比较三种算法的正确率、召回率及时间，比较结果见表5。
[0119]
表5 电力市场仿真数据测试结果
[0120][0121]
从表5中可以看出在仅知道少量数据样本标签的情况下，本文提出的 k-ctsvm与svm、tsvm相比，三者正确率相当，但k-ctsvm召回率远高于svm 和tsvm，这说明k-ctsvm比前两者的识别效果更加准确、全面，更适合实际电力市场中发电企业滥用市场力的识别。从消耗时间上看，tsvm每次增大无标签样本惩罚系数的过程都包含多次svm训练，时间复杂度远高于svm。但由于 k-ctsvm算法采取了更为高效的变分不等式求解，因此比用smo算法求解tsvm 的时间要短。此外，svm使用cppa算法的求解速度要远快于smo算法，这也说明了cppa求解算法的优越性。因此本文所提出的方法可以快速有效地将发电企业滥用市场力行为识别出来。
[0122]
实际电力市场数据：
[0123]
为了进一步验证本发明所提方法在实际电力市场具有可行性，选取某省50 个发电企业报价数据进行测试。由于实际电力市场中现有数据仅有成交价格和成交电量数据，无申报电量数据，我们删去报价成功比指标。且数据是一段式报价，高报价次数指标与是否为本段高报价指标重合，因此将高报价次数指标改为是否为本段高报价与是否为本段高份额之和。其中是否为本段高报价指标计算方式：是取值为1，不是为0。是否为本段的高份额指标计算方式：将成交电量份额从高到低排序，选择前30％取其值为1，其余取值为0。其中有标签样本占总样本的20％，违规样本占总体的10％，其余为未违规样本。将归一化处理后的数据分别代入k-ctsvm以及svm中对无标签样本进行测试，测试结果见表 6。
[0124]
表6 实际电力市场数据测试
[0125][0126]
由表6可知本文所提出的k-ctsvm算法与svm、tsvm相比，正确率和召回率更高。这说明k-ctsvm作为一种半监督算法，比一般支持向量机更适合对有标签样本少的数据集进行测试，更加适合识别实际电力市场中发电企业的违规行为。从时间上看，用变分不等式求解的k-ctsvm算法要比用smo算法求解的 tsvm快得多，因此本发明采用的求解方法更加高效，更能满足发电企业滥用市场力实时监测的需求。