油气浓度大数据智能检测系统

1.本发明涉及油气浓度检测的自动化装备的技术领域，具体涉及一种油气浓度大数据智能检测系统。


背景技术：

2.汽油为易挥发性物质，使用时不可避免会出现油气泄漏问题。我国对汽油气在生产、运输、存储过程中的允许泄漏量制定了严格的标准。传统的油气泄漏检测主要集中于回收系统的检测，如美国早期的isd系统、德国的vaporix系统等，但上述的这些系统无一例外的都是通过对回收系统气液比等关键参数进行测量计算来检测故障并报警，无法直观的看出泄漏问题，因此当前需要一种实时、可靠性好且高效的泄漏检测方法。发明一种油气浓度大数据智能检测系统采用数据采集处理和网络通信技术，设计了在线监测系统对汽油生产、运输、存储过程的油气浓度参数进行在线实时监测，提高汽油生产、运输和存储过程统的可靠性和安全性。


技术实现要素：

3.本发明提供一种油气浓度大数据智能检测系统；本发明有效解决了现有油气浓度没有根据油气浓度变化的非线性、大滞后和耦合性等对油气浓度的影响，没有对油气浓度进行精确预测，从而极大的影响油气企业安全生产的可靠运行和智能化管理问题。
4.本发明通过以下技术方案实现：
5.一种油气浓度大数据智能检测系统由测量参数采集平台和多点油气浓度预测子系统两部分组成，测量参数采集平台实现对测量参数精确检测，多点油气浓度预测子系统实现对测量参数进行处理和油气浓度预测，提高检测油气浓度的准确性和可靠性。
6.本发明进一步技术改进方案是：
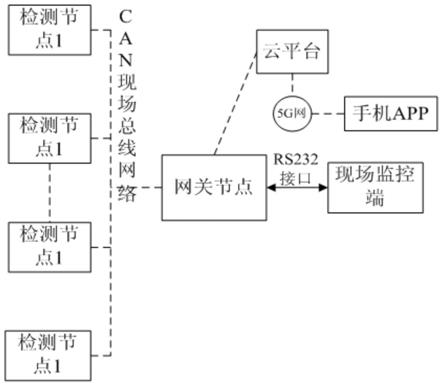
7.测量参数采集平台包括测量参数的检测节点、网关节点、现场监控端、云平台和移动端app组成，检测节点和网关节点之间通过构建can通信网络来实现检测节点和网关节点之间的通信；检测节点将检测的测量参数通过网关节点的rs232接口发送给现场监控端并对油气浓度进行预测；网关节点通过nb-iot模块与云平台之间和云平台通过5g网络与移动端app之间实现测量参数的双向传输，网关节点与现场监控端之间通过rs232接口实现测量参数信息的双向传输，移动端app为管理人员提供实时测量参数，检测节点的传感器采集的测量参数都已上传至云平台的数据库中，管理人员通过移动端app在远程查看当前的测量参数信息；测量参数采集平台结构和功能见图1所示。
8.本发明进一步技术改进方案是：
9.多点油气浓度预测子系统由参数检测模块、检测参数融合模型和二元联系数的drnn神经网络预测模型组成；参数检测模块包括多个参数检测模型，多个油气浓度传感器、多个温度传感器、多个风速传感器分别感知被检测环境的油气浓度值、温度值和风速值分别作为对应的参数检测模块的多个参数检测模型的输入，3个参数检测模块的多个参数检
测模型输出分别作为对应的检测参数融合模型的输入，3个检测参数融合模型输出作为二元联系数的drnn神经网络预测模型的对应输入，二元联系数的drnn神经网络预测模型输出油气浓度的确定值a和波动值b构成油气浓度的二元联系数为a+bi，油气浓度的确定值a和波动值b分别作为二元联系数的drnn神经网络预测模型的对应输入，二元联系数的drnn神经网络预测模型输出作为油气浓度的二元联系数值；多点油气浓度预测子系统结构和功能见图2所示。
10.本发明进一步技术改进方案是：
11.参数检测模型由带时滞单元的adaline神经网络模型、emd经验模态分解模型、gm(1，1)灰色预测模型、多个narx神经网络预测模型、2个按拍延迟线tdl、2个arima预测模型和二元联系数的小波神经网络模型组成；参数检测传感器输出作为带时滞单元的adaline神经网络模型的输入，带时滞单元的adaline神经网络模型输出作为emd经验模态分解模型的输入，emd经验模态分解模型输出的测量参数低频趋势值作为gm(1，1)灰色预测模型的输入，emd经验模态分解模型输出的多个测量参数高频趋势值分别作为对应的多个narx神经网络预测模型的输入，gm(1，1)灰色预测模型输出和多个narx神经网络预测模型输出分别作为二元联系数的小波神经网络模型的对应输入，二元联系数的小波神经网络模型输出测量参数的确定值c和波动值d构成测量参数的二元联系数为c+di，测量参数的确定值c和波动值d分别作为对应的2个按拍延迟线tdl的对应输入和二元联系数的小波神经网络模型的对应输入，2个按拍延迟线tdl输出分别作为对应的arima预测模型的输入，2个arima预测模型输出作为二元联系数的小波神经网络模型的对应输入，二元联系数的小波神经网络模型输出作为被测量参数的二元联系数值。参数检测模型结构和功能见图3所示。
12.本发明进一步技术改进方案是：
13.检测参数融合模型设计
14.(1)、一段时间多个参数检测模型输出的参数测量传感器的二元联系数构成时间序列二元联系数值阵列，每个参数测量传感器的时间序列二元联系数值的正理想值贴近度除以该参数测量传感器的时间序列二元联系数值的负理想值贴近度与该参数测量传感器的时间序列二元联系数值的正理想值贴近度的和得到的商为每个参数测量传感器的时间序列二元联系数值的距离相对贴近度；每个参数测量传感器的时间序列二元联系数值的距离相对贴近度除以所有参数测量传感器的时间序列二元联系数值的距离相对贴近度的和得到的商为每个参数测量传感器的时间序列二元联系数值的距离贴近度融合权重；
15.(2)、每个参数测量传感器的时间序列二元联系数值与二元联系数阵列的正理想值之间的灰色关联度除以该参数测量传感器的时间序列二元联系数值与二元联系数阵列的正理想值之间的灰色关联度相加该参数测量传感器的时间序列二元联系数值与二元联系数阵列的负理想值之间的灰色关联度的和得到的商为该参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度；每个参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度除以所有参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度的和得到的商为该参数测量传感器的时间序列二元联系数值的灰色关联度融合权重；
16.(3)、每个参数测量传感器的时间序列二元联系数值的均方根组合权重和线性组合权重重按照从小到大排序构成该参数测量传感器的时间序列二元联系数值的二元联系数融合权重，同一时刻每个参数测量传感器的时间序列二元联系数值与该参数测量传感器
的时间序列二元联系数值的二元联系数融合权重的积相加得到的和为所有参数测量传感器的时间序列二元联系数融合值；检测参数融合模型结构和功能见图2所示。
17.本发明与现有技术相比，具有以下明显优点：
18.一、本发明通过emd经验模态分解模型将原始带时滞单元的adaline神经网络模型输出序列分解为不同频段的分量，每一个分量都显示出隐含在原序列中的不同特征信息。以降低序列的非平稳性。测量参数的高频波动部分数据关联性不强，频率比较高，代表原始序列的波动成分，具有一定的周期性和随机性，这与测量参数过程的周期性变化相符合；低频成分代表测量参数过程原序列的变化趋势。可见emd经验模态分解能够逐级分解出测量参数过程的波动成分、周期成分和趋势成分，分解出的每一个分量自身包含相同的变形信息，在一定程度上减少了不同特征信息之间的相互干涉，且分解出的各分量变化曲线比原始测量参数变形序列曲线光滑。可见emd经验模态分解能有效分析多因素共同作用下的参数测量过程变形数据，分解得到的各分量有gm(1，1)灰色预测模型输出和多个narx神经网络预测模型的建立和更好地预测。最后将各分量预测结果叠加得到最终融合预测结果。实例研究表明，所提的融合预测结果具有较高的预测精度。
19.二、本发明采用gm(1,1)灰色预测模型预测参数测量过程中测量参数低频趋势的时间跨度长。用gm(1,1)灰色预测模型模型可以根据测量参数低频趋势值预测未来时刻测量参数低频趋势值，用上述方法预测出的测量参数低频趋势后，把测量参数低频趋势值再加分别加入测量参数低频趋势的原始数列中，相应地去掉数列开头的一个数据建模，再进行预测测量参数低频趋势的预测。依此类推，预测出测量参数低频趋势值。这种方法称为等维灰数递补模型，它可实现较长时间的预测。可以更加准确地掌握测量参数低频趋势的变化趋势，为有效避免测量参数低频趋势波动做好准备。
20.三、本发明采用arima预测模型基于测量参数的确定值和波动值的原始数据服从时间序列分布，利用测量参数的确定值和波动值变化均具有一定惯性趋势的原理，整合了趋势因素、周期因素和随机误差等因素的测量参数的确定值和波动值的原始时间序列变量，通过差分数据转换等方法将非平稳序列转变为零均值的平稳随机序列，通过反复识别和模型诊断比较并选择理想的模型进行测量参数的确定值和波动值数值拟合和预测。采用arima预测模型方法结合了自回归和移动平均方法的长处，具有不受数据类型束缚和适用性强的特点，是一种短期预测测量参数确定值和波动值的模型。
21.四、本发明narx神经网络预测模型是一种通过引入多个模糊最小二乘支持向量机模型的延时模块及反馈实现来建立narx神经网络预测模型动态递归网络，它是沿着测量参数在时间轴方向的拓展的多个时间测量参数参数的序列来实现及函数模拟功能的数据关联性建模思想，该方法通过一段时间内测量参数的特征值来建立测量参数预测的组合模型，模型输出的测量参数在反馈作用中被作为输入而闭循环训练提高神经网络的计算精确度，实现对测量参数的连续动态检测。
22.五、本发明针对参数测量过程中，传感器精度误差、干扰和测量值异常等问题存在的不确定性和随机性，本发明专利将参数传感器测量的参数值通过参数检测模型转化为二元联系数形式表示，有效地处理了参数传感器测量参数的模糊性、动态性和不确定性，提高了参数传感器值检测参数的客观性和可信度。
附图说明
23.图1为本发明的测量参数采集平台；
24.图2为本发明的多点油气浓度预测子系统；
25.图3为本发明的参数检测模型；
26.图4为本发明的检测节点；
27.图5为本发明的网关节点；
28.图6为本发明的现场监控端软件功能图。
具体实施方式
29.结合附图1-6，对本发明技术方案作进一步描述：
30.一、系统总体功能的设计
31.本发明一种油气浓度大数据智能检测系统由由测量参数采集平台和多点油气浓度预测子系统两部分组成，测量参数采集平台实现对油气浓度和影响油气浓度的参数进行检测，多点油气浓度预测子系统实现对测量参数进行处理与预测；测量参数采集平台包括测量参数的检测节点、网关节点、现场监控端、云平台和手机app组成，检测节点构建成can总线网络通信来实现检测节点和网关节点之间的can现场总线网络通信；检测节点将检测的测量参数通过网关节点发送给现场监控端和云平台，网关节点、云平台、现场监控端和手机app之间实现测量参数和相关控制信息的双向传输。测量参数采集平台见图1所示。
32.二、检测节点的设计
33.采用大量基于can总线通信网络的检测节点作为测量参数感知终端，检测节点通过can总线通信网络实现与网关节点之间的信息相互交互。检测节点包括采集油气浓度、温度和风速的传感器和对应的信号调理电路、msp430单片机和can总线网络通信的can总线接口；检测节点的软件主要实现can总线网络通信和测量参数的采集与预处理。软件采用c语言程序设计，兼容程度高，大大提高了软件设计开发的工作效率，增强了程序代码的可靠性、可读性和可移植性。检测节点结构见图4。
34.三、网关节点设计
35.网关节点包括can接口、nb-iot模块、msp430单片机和rs232接口，网关节点包括can接口实现与检测节点之间通信的can现场总线通信网络，nb-iot模块实现网关节点与云平台之间的数据双向交互，rs232接口连接现场监控端，实现网关与现场监控端之间的信息交互。网关节点结构见图5。
36.四、现场监控端的软件设计
37.现场监控端是一台工业控制计算机，现场监控端主要实现对测量参数进行采集与处理和预测，实现与检测节点与网关节点的信息交互，现场监控端主要功能为通信参数设置、数据分析与数据管理和通过多点油气浓度预测子系统对测量参数进行智能处理与预测，该管理软件选择了microsoft visual++6.0作为开发工具，调用系统的mscomm通信控件来设计通讯程序，现场监控端软件功能见图5；多点油气浓度预测子系统结构如图2所示，多点油气浓度预测子系统由参数检测模块、检测参数融合模型和二元联系数的drnn神经网络预测模型组成，多点油气浓度预测子系统的设计过程如下：
38.参数检测模块包括多个参数检测模型，多个油气浓度传感器、多个温度传感器、多
个风速传感器分别感知被检测环境的油气浓度值、温度值和风速值分别作为对应的参数检测模块的多个参数检测模型的输入，3个参数检测模块的多个参数检测模型输出分别作为对应的检测参数融合模型的输入；参数检测模型的结构功能见图3所示；
39.1、参数检测模型设计
40.参数检测模型由带时滞单元的adaline神经网络模型、emd经验模态分解模型、gm(1，1)灰色预测模型、多个narx神经网络预测模型、2个按拍延迟线tdl、2个arima预测模型和二元联系数的小波神经网络模型组成；
41.(1)、带时滞单元的adaline神经网络模型设计
42.参数检测传感器输出作为带时滞单元的adaline神经网络模型的输入，带时滞单元的adaline神经网络模型输出作为emd经验模态分解模型的输入；带时滞单元的adaline神经网络模型由2个按拍延迟线tdl和adaline神经网络组成，参数传感器输出作为对应的按拍延迟线tdl的输入，该按拍延迟线tdl的输出作为adaline神经网络的输入，adaline神经网络的输出作为对应的按拍延迟线tdl的输入，该按拍延迟线tdl的输出为带时滞单元的adaline神经网络模型的输出；adaline神经网络模型的自适应线性单元(adaptive linear element)是早期的神经网络模型之一，该模型的输入信号可写成向量的形式:x(k)＝[x0(k),x1(k),
…
xn(k)]
t
，每一组输入信号对应有一组权值向量相对应表示为:w(k)＝[k0(k),k1(k),
…
k(k)]，x0(k)等于负1时是adaline神经网络模型的偏置值决定神经元的兴奋或抑制状态，可根据adaline神经网络模型的输入向量和权值向量定义网络输出为：
[0043][0044]
在adaline神经网络模型中，有一特殊输入即理想响应输出d(k)，把它送入adaline神经网络模型中，然后通过网络的输出y(k)进行比较，将差值送到学习算法机制中，以调整权向量直到获得最佳权向量，y(k)与d(k)趋向一致，权向量的调整过程即为网络的学习过程，学习算法是学习过程的核心部分，adaline神经网络模型的权值优化搜索算法采用lms算法最小二乘法。
[0045]
(2)、emd经验模态分解模型设计
[0046]
带时滞单元的adaline神经网络模型输出作为emd经验模态分解模型的输入，emd经验模态分解模型输出的测量参数低频趋势值作为gm(1，1)灰色预测模型的输入；emd经验模态分解模型输出的多个测量参数高频趋势值分别作为对应的多个narx神经网络预测模型的输入；emd经验模态分解是一种自适应信号筛选方法，具有计算简单、直观、基于经验和自适应的特点。它能将存在于测量参数信号中不同特征的趋势逐级筛选出来，得到多个高频波动部分(imf)和低频趋势部分。emd经验模态分解出来的imf分量包含了测量参数信号从高到低不同频率段的成分，每个频率段包含的频率分辨率都随信号本身变化，具有自适应多分辨分析特性。使用emd经验模态分解的目的就是为了更准确地提取故障信息。imf分量必须同时满足两个条件：
①
在待分解参数测量信号中，极值点的数目与过零点的数目相等，或最多相差一个；
②
在任一时间上，由局部极大值和局部极小值定义的包络均值为零。emd经验模态分解方法针对带时滞单元的adaline神经网络模型输出值信号的“筛分”过程步骤如下：
[0047]
(a)带时滞单元的adaline神经网络模型输出值信号所有的局部极值点，然后用三
次样条线将左右的局部极大值点连接起来形成上包络线。
[0048]
(b)在用三次样条线将带时滞单元的adaline神经网络模型输出值的局部极小值点连接起来形成下包络线，上、下包络线应该包络所有的数据点。
[0049]
(c)上、下包络线的平均值记为m1(t)，求出：
[0050]
x(t)-m1(t)＝h1(t)
ꢀꢀꢀꢀꢀꢀ
(2)
[0051]
x(t)为带时滞单元的adaline神经网络模型输出值原始信号，如果h1(t)是一个imf，那么h1(t)就是x(t)的第一个imf分量。记c1(t)＝h
1k
(t)，则c1(t)为信号x(t)的第一个满足imf条件的分量。
[0052]
(d)将c1(t)从x(t)中分离出来，得到：
[0053]
r1(t)＝x(t)-c1(t)
ꢀꢀꢀꢀꢀꢀꢀ
(3)
[0054]
将r1(t)作为原始数据重复步骤(a)-步骤(c)，得到x(t)的第2个满足imf条件的分量c2。重复循环n次，得到信号x(t)的n个满足imf条件的分量。这样通过emd经验模态分解模型把带时滞单元的adaline神经网络模型输出分解为低频趋势部分和多个高频波动部分，emd经验分解模型如图3所示。
[0055]
(3)、gm(1，1)灰色预测模型设计
[0056]
emd经验模态分解模型输出的测量参数低频趋势值作为gm(1，1)灰色预测模型的输入，gm(1，1)灰色预测模型输出和多个narx神经网络预测模型输出分别作为二元联系数的小波神经网络模型的对应输入；；gm(1，1)灰色预测方法较传统的统计预测方法有着较多的优点，它不需要确定预测变量是否服从正态分布，不需要大的样本统计量，不需要根据测量参数低频趋势值输入变量的变化而随时改变预测模型，通过累加生成技术，建立统一的微分方程模型，累加测量参数低频趋势原始值还原后得出预测结果，微分方程模型具有更高的预测精度。建立gm(1，1)灰色预测模型的实质是对低频趋势值原始数据作一次累加生成，使生成数列呈现一定规律，通过建立微分方程模型，求得拟合曲线，用以对参数测量低频趋势值进行预测。
[0057]
(4)、多个narx神经网络预测模型设计
[0058]
emd经验模态分解模型输出的多个测量参数高频趋势值分别作为对应的多个narx神经网络预测模型的输入，gm(1，1)灰色预测模型输出和多个narx神经网络预测模型输出分别作为二元联系数的小波神经网络模型的对应输入；narx神经网络预测模型是一种带输出反馈连接的动态递归神经网络，在拓扑连接关系上可等效为有输入时延的bp神经网络加上输出到输入的时延反馈连接，其结构由输入层、时延层、隐层和输出层构成，其中输入层节点用于信号输入，时延层节点用于输入信号和输出反馈信号的时间延迟，隐层节点利用激活函数对时延后的信号做非线性运算，输出层节点则用于将隐层输出做线性加权获得最终网络输出。narx神经网络第i个隐层节点的输出hi为：
[0059][0060]
narx神经网络第j个输出层节点输出oj为：
[0061]
[0062]
本发明专利的narx神经网络包括输入层、时延层、隐层和输出层。
[0063]
(5)、arima预测模型设计
[0064]
2个按拍延迟线tdl输出分别作为对应的arima预测模型的输入，2个arima预测模型输出作为二元联系数的小波神经网络模型的对应输入；arima(auto regressive integrated moving average)预测模型是自回归积分滑动平均模型，它将自回归模型(autoregressive，ar)和滑动平均模型(moving average，ma)有机地组合起来，使之成为一种综合的预测方法。作为有效的现代数据处理方法之一，它被誉为时间序列预测方法中最复杂最高级的模型，在实际应用中，由于输入原始数据序列往往表现出一定的趋势或循环特征，不满足arma模型对时间序列的平稳性要求，而取差分是消除数据趋势性的一种方便和有效的方法。基于差分后的数据序列建立的模型称为arima预测模型，记为{xt}-arima(p，d，q)，其中p、q称为模型的阶，d表示差分的次数。显然，当d为0时，arima预测模型为arma模型，其定义为:
[0065]
x
t
＝b1x
t-1
+
…
+b
p
x
t-p
+ε
t
+a1ε
t-1
+
…
+aqε
t-q
ꢀꢀꢀ
(6)
[0066]
{x
t
}为要预测的二元联系数的小波神经网络输出的压力确定值a和波动值b的数据序列，{ε
t
}～wn(0,σ2)。arima预测模型建立主要包括模型的识别、参数估计和模型诊断。模型识别主要包括时间序列的预处理和模型参数的初步定阶；模型定阶完成之后需要通过时间序列观察值并结合p，d，q值来对模型中的未知参数进行估计；模型的诊断主要是针对整个模型的显著性检验和模型中参数的显著性检验。通常模型的建立是个不断优化的过程，模型优化常用的为aic和bic准则，即最小信息量准则其值越小，模型越合适，bic准则是针对aic准则对大样本序列的不足所做的改进。
[0067]
(6)、二元联系数的小波神经网络模型设计
[0068]
gm(1，1)灰色预测模型输出和多个narx神经网络预测模型输出分别作为二元联系数的小波神经网络模型的对应输入，二元联系数的小波神经网络模型输出测量参数的确定值c和波动值d构成测量参数的二元联系数为c+di，测量参数的确定值c和波动值d分别作为对应的2个按拍延迟线tdl的对应输入和二元联系数的小波神经网络模型的对应输入，2个按拍延迟线tdl输出分别作为对应的arima预测模型的输入，2个arima预测模型输出作为二元联系数的小波神经网络模型的对应输入，二元联系数的小波神经网络模型是输出为二元联系数的小波神经网络模型，小波神经网络模型wnn(wavelet neural networks)是在小波理论基础上，结合人工神经网络而提出的一种前馈型网络。它是以小波函数为神经元的激励函数，小波的伸缩、平移因子以及连接权重，在对误差能量函数的优化过程中被自适应调整。设小波神经网络模型的输入信号可以表示为输入的一维向量xi(i＝1,2,
…
,n)，输出信号表示为yk(k＝1,2,
…
,m)，小波神经网络模型输出层输出值的计算公式为：
[0069][0070]
公式中ω
ij
输入层i节点和隐含层j节点间的连接权值，为小波基函数，bj为小波基函数的平移因子，aj小波基函数的伸缩因子，ω
jk
为隐含层j节点和输出层k节点间的连接权值。本专利中的小波神经网络模型的权值和阈值的修正算法采用梯度修正法来更新网络权值和小波基函数参数，从而使小波神经网络输出不断逼近期望输出。二元联系数的小
波神经网络模型输出作为被测量参数的二元联系数值。
[0071]
2、检测参数融合模型设计
[0072]
①
、构建参数测量传感器的时间序列二元联系数阵列
[0073]
一段时间多个参数检测模型输出的二元联系数构成参数测量传感器的时间序列二元联系数阵列，设有n个参数测量传感器和m个时刻的nm个参数测量传感器的二元联系数值构成n行和m列的参数测量传感器的时间序列二元联系数阵列，设同一参数测量传感器的不同时刻二元联系数值为a
ij
(t),a
ij
(t+1),
…
,a
ij
(m)，则所有参数测量传感器的时间序列二元联系数阵列为：
[0074][0075]
②
、计算参数测量传感器的时间序列二元联系数值的距离融合权重
[0076]
同一时刻所有参数测量传感器的二元联系数的平均值构成二元联系数阵列的正理想值，二元联系数阵列的正理想值为：
[0077]
同一时刻所有参数测量传感器的二元联系数值与对应的二元联系数阵列的正理想值贴近度最小的二元联系数值构成二元联系数阵列的负理想值，二元联系数阵列的负理想值为：
[0078][0079]
每个参数测量传感器的时间序列二元联系数值的正理想值贴近度是每个参数测量传感器的时间序列二元联系数与二元联系数阵列的正理想值的贴近度为：
[0080][0081]
每个参数测量传感器的时间序列二元联系数值的负理想值贴近度是每个参数测量传感器的时间序列二元联系数值与二元联系数阵列的负理想值的贴近度为：
[0082][0083]
每个参数测量传感器的时间序列二元联系数值的正理想值贴近度除以该参数测量传感器的时间序列二元联系数值的负理想值贴近度与该参数测量传感器的时间序列二元联系数值的正理想值贴近度的和得到的商为每个参数测量传感器的时间序列二元联系数值的距离相对贴近度，公式为：
[0084][0085]
通过(16)公式计算可以知道，每个参数测量传感器的时间序列二元联系数值的距离相对贴近度越大，则该参数测量传感器的时间序列二元联系数值与对应的正理想值就越接近，否则该参数测量传感器的时间序列二元联系数值与对应的正理想值就越远，根据这个原理确定每个参数测量传感器的时间序列二元联系数值的距离相对贴近度除以所有参数测量传感器的时间序列二元联系数值的距离相对贴近度的和得到的商为每个参数测量传感器的时间序列二元联系数值的距离贴近度融合权重为：
[0086][0087]
③
、计算参数测量传感器的时间序列二元联系数值的灰色关联度融合权重
[0088]
每个参数测量传感器的时间序列二元联系数值与二元联系数阵列正理想值的灰色关联度为：
[0089][0090]
通过计算每个参数测量传感器的时间序列二元联系数值与二元联系数阵列正理想值的灰色关联度，可以构建每个参数测量传感器的时间序列二元联系数值的灰色关联度矩阵：
[0091][0092]
根据公式(16)可以得到每个参数测量传感器的时间序列二元联系数值与时间序列参数测量传感器的二元联系数阵列正理想值之间的灰色关联度，如下公式所示：
[0093][0094]
同理，每个参数测量传感器的时间序列二元联系数值与时间序列参数测量传感器的二元联系数阵列负理想值的灰色关联度为，定义如下公式：
[0095][0096]
同理，通过计算每个参数测量传感器的时间序列二元联系数值与二元联系数阵列负理想值的灰色关联度，可以构建每个参数测量传感器的时间序列二元联系数值的灰色关联度矩阵：
[0097][0098]
根据公式(19)可以得到每个参数测量传感器的时间序列二元联系数值与二元联系数阵列的负理想值之间的灰色关联度，如下公式所示：
[0099][0100]
每个参数测量传感器的时间序列二元联系数值与二元联系数阵列的正理想值之间的灰色关联度除以该参数测量传感器的时间序列二元联系数值与二元联系数阵列的正理想值之间的灰色关联度相加该参数测量传感器的时间序列二元联系数值与二元联系数阵列的负理想值之间的灰色关联度的和得到的商为该参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度为：
[0101][0102]
通过(21)公式计算可以知道，每个参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度越大，则该参数测量传感器的时间序列二元联系数值与对应的二元联系数阵列的正理想值的形状相似度越大，否则该参数测量传感器的时间序列二元联系数值与对应的二元联系数阵列的正理想值的形状相似度越小，根据这个原理确定每个参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度除以所有参数测量传感器的时间序列二元联系数值的灰色关联相对贴近度的和得到的商为该参数测量传感器的时间序列二元联系数值的灰色关联度融合权重为：
[0103][0104]
④
、计算多个参数测量传感器的时间序列二元联系数值的融合值
[0105]
根据每个参数测量传感器的时间序列二元联系数值的距离融合权重αi和灰色关联度融合权重βi，求取均方根组合权重γi，显然γi与αi、βi和都应尽可能接近，根据最小相对信息熵原理有：
[0106][0107]
用拉格朗日乘子法解上述优化问题得：
[0108][0109]
根据公式(24)可以知每个参数测量传感器的时间序列二元联系数值的距离融合
权重和灰色关联度融合权重乘积的均方根占所有参数测量传感器的时间序列二元联系数值的距离融合权重和灰色关联度融合权重乘积的均方根和的比为该参数测量传感器的时间序列二元联系数值融合的均方根组合权重。
[0110]
根据参数测量传感器的时间序列二元联系数值的距离融合权重αi和灰色关联度融合权重βi进行线性组合得到该参数测量传感器的时间序列二元联系数值融合的线性组合权重θi，公式为：
[0111]
θi＝ααi+ββiꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(25)
[0112]
根据公式(27)和公式(28)得到该参数测量传感器的时间序列二元联系数值融合的二元联系数融合权重为wi：
[0113]
wi＝[min(θi,γi),max(θi,γi)]
ꢀꢀꢀꢀꢀ
(26)
[0114]
从公式(26)可以知每个参数测量传感器的时间序列二元联系数值的均方根组合权重、线性组合权重重按照从小到大排序构成该参数测量传感器的时间序列二元联系数值的组合融合权重。根据同一时刻每个参数测量传感器的时间序列二元联系数值与该参数测量传感器的时间序列二元联系数值的组合融合权重的积相加得到的和为所有参数测量传感器的时间序列二元联系数融合值为：
[0115][0116]
3、二元联系数的drnn神经网络预测模型设计
[0117]
3个检测参数融合模型输出作为二元联系数的drnn神经网络预测模型的对应输入，二元联系数的drnn神经网络预测模型输出油气浓度的确定值a和波动值b构成油气浓度的二元联系数为a+bi，油气浓度的确定值a和波动值b分别作为二元联系数的drnn神经网络预测模型的对应输入；二元联系数的drnn神经网络预测模型为输出和输入都是二元联系数的drnn神经网络模型，二元联系数的drnn神经网络预测模型为3层网络结构，其隐层为回归层，在本专利二元联系数的drnn神经网络预测模型中，设i＝[i1(t),i2(t),
…
,in(t)]为网络输入向量，其中ii(t)为二元联系数的drnn神经网络预测模型第i个神经元t时刻的输入，回归层第j个神经元的输出为xj(t)，sj(t)为第j个回归神经元输入总和，f(
·
)为s的函数，则o(t)为二元联系数的drnn神经网络预测模型输出。则二元联系数的drnn神经网络预测模型输出为：
[0118][0119]
二元联系数的drnn神经网络预测模型输出作为油气浓度的二元联系数值。
[0120]
五、一种油气浓度大数据检测系统的设计举例
[0121]
根据油气浓度检测系统的实际状况，系统布置测量参数采集平台的检测节点、网关节点和现场监控端的平面布置安装图，其中检测节点的传感器根据检测的需要均衡布置在油气浓度挥发的各个方位，通过该系统实现对油气浓度参数进行采集与预测。
[0122]
本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰这些改进和润饰也视为本发明的保护范围。