一种模拟风力机尾流的修正致动线模型方法

1.本发明涉及一种模拟风力机尾流的修正致动线模型方法，属于制动模型计算风力机尾流技术领域。


背景技术：

2.风能是一种重要的可再生能源，我国陆地70m高度层年平均风功率密度达到300w/m2以上的风能资源技术可开发量为2.6tw，开发利用价值巨大。在大型风电场，必然有风力机处于上游风力机的尾迹中，从而降低来流风速，增加尾流所附加的风剪切和强湍流。近年来，采用cfd模拟尾流效应成为研究热点。
3.现有技术中，采用致动线模型对风力机的尾流开展数值模拟取得了较好的预测精度，但由于均没有考虑叶尖叶根损失、三维翼型延迟失速以及机舱和塔架的影响，在中心涡和叶尖涡的生成预测中还存在误差的问题。


技术实现要素：

4.为解决现有技术的不足，本发明的目的在于提供一种模拟风力机尾流的修正致动线模型方法，建立了全尺寸风力机致动线模型，运用改进制动线模型对风力机的尾流场进行数值模拟计算，实验数据和未修正模型在风力机功率系数、推力系数、尾流速度方面的对比，验证了修正后的风力机致动线模型的准确性。
5.为了实现上述目标，本发明采用如下的技术方案：
6.一种模拟风力机尾流的修正致动线模型方法，包括如下步骤：
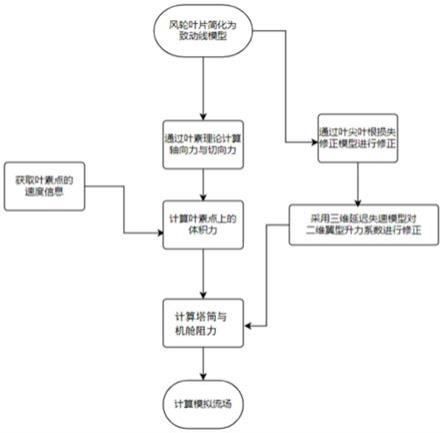
7.将风轮叶片简化为致动线模型；
8.获取叶素点中的速度信息；
9.通过叶素理论计算叶素点处轴向力和切向力；
10.计算叶素点上的体积力；
11.通过叶尖叶根损失修正模型进行修正；
12.采用三维延迟失速模型对二维翼型升力系数进行修正；
13.计算塔筒与机舱阻力；
14.计算模拟流场。
15.进一步地，前述将风轮叶片简化为致动线模型的具体步骤包括：
16.将旋转的风轮叶片简化成一条假想的线段，并将其分成若干段叶素；
17.通过公式确定叶片旋转过程中各叶素点的三维坐标，所述公式为：
18.xi＝x
wt
+rcosφ
19.yi＝y
wt
+rcosφ
20.zi＝z
wt
+rsinφ
21.其中，xi、yi、zi为叶素点i的三维坐标；r为展长；φ为叶片的旋转角度；x
wt
、y
wt
、z
wt
为风力机轮毂中心的三维坐标。
22.进一步地，前述获取叶素点中的速度信息的具体方法如下：
23.在cfd流场中，寻找离叶素点最近的网格型心，然后将该网格型心存储的速度信息赋给叶素点；
24.若满足则ui＝u
cell
+gradu*ds，式中x
i_cell
为网格型心坐标；dxi为网格尺寸；ui为叶素点处的速度；u
cell
是距离该叶素点最近的网格型心速度；gradu为流场速度梯度；ds为该叶素点到最近网格型心的距离。
25.进一步地，前述通过叶素理论计算轴向力和切向力的方法包括：
26.将赋值的叶素点处速度带入公式得到轴向力t和切向力fn，所述公式为
[0027][0028]
其中，总速度轴向速度切向速度为
[0029]
式中，ρ是空气密度，是轴向法向量，c是翼型的弦长，入流角c
l
是升力系数，cd是阻力系数，迎角β为所在叶素的扭角，dr为叶素展长，是叶素点处的速度，是角速度，是矢量半径。
[0030]
进一步地，前述计算叶素点上的体积力的步骤包括：
[0031][0032]
式中，f
x
/fy/fz分别代表叶素点在xyz方向的体积力；γ是风力机顺时针偏航的角度；δ是叶片的旋转角度；b是叶片数；i是所在叶素点的编号；
[0033]
采用三维高斯分布函数进行体积力光顺，流场中某一网格型心点受到的体积力fm为：
[0034][0035]
式中，d为型心点和叶素之间的距离；ε是光顺参数。
[0036]
进一步地，前述通过叶尖叶根损失修正模型进行修正的过程如下：
[0037]
带入公式，求得叶尖修正系数f1和叶根修正系数f
hub
，所述公式为：
[0038]
[0039]
式中，g＝exp(-0.125(bλ-21))+0.1；λ是叶尖速比；r为叶片半径；r
hub
为风力机转子叶根处半径；r是叶素展长；b是叶片数；为入流角。
[0040]
进一步地，前述采用三维延迟失速模型对二维翼型升力系数进行修正过程如下：
[0041]
对叶片3/4展长以下的部分进行修正，带入公式求三维翼型升力系数c
l,3d
和迎角变化度数δα，所述公式为：
[0042][0043]
式中，为升力系数直线段斜率；δα为迎角变化度数；c
l,3d
为三维翼型升力系数；c
l,2d
为二维翼型升力系数；α
max
为最大升力系数对应的迎角；α0为升力系数为零时对应的迎角；c为叶片弦长；n为经验公式一般取为1.0；k为冯卡门常数。
[0044]
进一步地，前述致动线区域添加体积力的方法包括：
[0045]
带入公式，求得一个塔筒微元的气流轴向阻力df
x,tow
和机舱阻力f
nac
，所述公式为：
[0046][0047]
式中，u
tow
为该塔筒微元中心来流风速；ρ是空气密度；d
tow
为该塔筒微元中心圆形截面直径；dh为该塔筒微元高度；c
d,tow
为塔筒阻力系数取值1.0；a
nac
为机舱截面积；c
d,nac
为机舱阻力系数取值1.0；轴向速度机舱阻力系数取值1.0；轴向速度是轴向法向量，是叶素点处的速度。
[0048]
本发明所达到的有益效果：
[0049]
1、本发明可使得致动线模型的气动特性和尾流速度方面能够更好的吻合实验测试数据，在实际的工程中有很好的应用前景；
[0050]
2、为风力机尾流计算、风力机功率预测等工作提供理论支持。
附图说明
[0051]
图1是本发明修正致动线模型流程图；
[0052]
图2是本发明风轮转子的旋转；
[0053]
图3是本发明风力机源项模型；
[0054]
图4是本发明叶素受力分析；
[0055]
图5是本发明风力涡轮机g1模型；
[0056]
图6是g1模型修正尾流前-1d处风轮中心径向速度廓线；
[0057]
图7是g1模型修正尾流后2d处风轮中心径向速度廓线；
[0058]
图8是g1模型修正尾流后3d处风轮中心径向速度廓线；
[0059]
图9是g1模型修正尾流后4d处风轮中心径向速度廓线；
[0060]
图10是g1模型修正尾流后6d处风轮中心径向速度廓线；
[0061]
图11是g1模型修正尾流后9d处风轮中心径向速度廓线。
具体实施方式
[0062]
下面结合附图对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。
[0063]
如图1至图11所示，本发明所建立的一种基于修正致动线模型，具体步骤如下：
[0064]
步骤1：如图2所示，将旋转的风轮叶片简化成一条假想的线段，并将其分成若干段叶素，初步形成致动线模型，再通过步骤2)-步骤9)添加体积力到控制方程的源项中。
[0065]
最终得到图3所示的包括叶片、机舱、塔筒源项在内的全尺寸风力机致动线模型。
[0066]
步骤2：确定叶片旋转过程中各叶素点的三维坐标，计算公式如下：
[0067]
xi＝x
wt
+rcosφ
[0068]
yi＝y
wt
+rcosφ
[0069]
zi＝z
wt
+rsinφ
[0070]
其中，xi、yi、zi为叶素点i的三维坐标；r为展长；φ为叶片的旋转角度；x
wt
、y
wt
、z
wt
为风力机轮毂中心的三维坐标。
[0071]
步骤3：在cfd流场中，流场的信息诸如压力、速度、体积力源项等均保存在网格型心中，而叶片在计算区域内旋转时，叶素点不一定与网格型心重合，因此需要首先找到离叶素点最近的网格型心，然后将其存储的速度信息赋给叶素点。同时当网格型心坐标与叶素点坐标满足：此时有ui＝u
cell
+gradu*ds，式中x
i_cell
为网格型心坐标；dxi为网格尺寸；ui为叶素点处的速度；u
cell
是距离该叶素点最近的网格型心速度；gradu为流场速度梯度；ds为该叶素点到最近网格型心的距离。
[0072]
步骤4：如图4所示为相对于叶片的空气流相对速度以及轴向力和切向力的速度三角形，由叶素点处速度和叶素理论得到轴向力t和切向力fn：
[0073][0074]
其中，总速度轴向速度切向速度为
[0075][0076]
式中，ρ是空气密度，是轴向法向量，c是翼型的弦长，入流角升力系数c
l
和阻力系数cd由迎角和翼型气动数据得到；迎角β为所在叶素的扭角；dr为叶素展长；是叶素点处的速度；是角速度；是矢量半径。
[0077]
步骤5：叶片单元上的轴向力和切向力在笛卡尔坐标系中组合成三维体积力，计算公式:
[0078]
[0079]
式中，f
x
/fy/fz分别代表叶素点在xyz方向的体积力；γ是风力机顺时针偏航的角度；δ是叶片的旋转角度；b是叶片数；i是所在叶素点的编号。
[0080]
接着，采用三维高斯分布函数进行体积力光顺，流场中某一网格型心点受到的体积力为：式中，d为型心点和叶素之间的距离；ε是光顺参数与网格大小有关。
[0081]
步骤6：风力机在旋转过程中产生的叶尖涡与叶根涡脱落后进入尾流区，会对转子的诱导速度分布产生影响，对此采用叶尖叶根损失修正模型进行修正。
[0082]
进一步地，叶尖叶根损失修正模型中具体计算过程如下：
[0083][0084]
式中，g＝exp(-0.125(bλ-21))+0.1；f
hub
为叶根修正系数；f1为叶尖修正系数；λ是叶尖速比；r为叶片半径；r
hub
为风力机转子叶根处半径；r是叶素展长；b是叶片数；为入流角。
[0085]
步骤7：当风力机旋转时，叶片根部吸力面会存在一定的展向流动，进而产生指向叶素翼型尾缘的科氏力，它与风力机旋转产生的离心力共同作用，有助于抵抗叶片表面边界层内的逆压梯度，延迟边界层分离以提高翼型的升力系数，这便是风力机叶片三维失速延迟效应。对此，采用三维延迟失速模型对二维翼型的升力系数进行修正。
[0086]
进一步地，在对二维翼型升力系数进行修正时，是对叶片3/4展长以下的部分进行修正，具体的修正计算公式如下：
[0087][0088]
式中，c
l,3d
为三维翼型升力系数；δα为迎角变化度数；为升力系数直线段斜率；c
l,2d
为二维翼型升力系数；α
max
为最大升力系数对应的迎角；α0为升力系数为零时对应的迎角；c为叶片弦长；n为经验公式一般取为1.0；k为冯卡门常数。
[0089]
步骤8：风力机的机舱和塔筒不仅能够使尾流中的速度发生衰减，还会影响尾流的湍动能，尤其是塔筒形成的绕流与叶片产生的尾流相互作用会加速叶尖涡的破裂，所以需要对计算塔筒与机舱阻力进行计算，计算公式：
[0090][0091]
式中，df
x,tow
为一个塔筒微元的气流轴向阻力；ρ是空气密度；f
nac
为机舱阻力；u
tow
为该塔筒微元中心来流风速；d
tow
为该塔筒微元中心圆形截面直径；dh为该塔筒微元高度；cd,tow
为塔筒阻力系数取值1.0；a
nac
为机舱截面积；c
d,nac
为机舱阻力系数取值1.0；u为轴向速度。
[0092]
步骤9：计算模拟流场：叶片旋转后，在每个时间步长上对制动线网格重复以上步骤进行识别。
[0093]
下面通过风力机g1作为修正致动线模型数值模拟验证的研究对象进行验证。风力机的风轮直径为1.1m，轮毂直径为0.03m，塔筒高度为0.8m，叶片设计采用rg14。以风力机g1为模型在入口风速为5m/s叶片半径为0.55m，额定转速为850rad
·
min-1
的工况下用修正致动线模型对风机尾流场进行了数值模拟并将结果与实验测量值进行比较，图5为风力涡轮机g1在流场中的位置，以及模型验证计算域的总长、宽和高。图6至图11为g1风力机尾流前-1d和尾流后2d、3d、4d、6d、9d共6个位置风轮中心径向平均风速与试验数据的对比，其中黑点代表着实验数据、虚线代表着致动线模型、实线代表着修正致动线模型。由图可知，由于修正了叶尖和根部的损失，修正致动线模型的中心尾迹(y/d＝0)速度比传统的致动线模型更接近实验值。在远尾流处，修正致动线模型值与实验值更接近。传统的致动线模型对推力系数和功率因数的预测精度较高，但由于叶尖和叶根的损失，对中心涡和叶尖涡的预测仍存在一定的误差。由上述分析可知修正模型与实验值的吻合程度优于未修正模型，能够较好的模拟出风力机尾流的风速衰减情况。
[0094]
表1为计算得到的推力系数、功率系数与实验测量值，由表数据可知修正后的风力机致动线模型在气动性能的预测结果上与实验值非常接近，且明显优于未修正模型，尤其是对推力系数的预测，这是由于修正模型考虑了风力机的叶尖和叶根损失，即载荷系数降低，因此计算得到的风轮推力低于未修正模型。
[0095][0096]
表1修正前后参数对比表
[0097]
以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。