一种曲面牙型形廓行星滚柱丝杠的优化设计方法与流程

1.本发明涉及一种曲面牙型形廓行星滚柱丝杠的优化设计方法，属于行星滚柱丝杠设计领域。


背景技术：

2.行星滚柱丝杠是一类具有体积小、承载高、集成性好等优点的传动部件，能在旋转运动和直线运动之间相互转化。其主要由丝杠、螺母和滚柱组成，三者之间以点接触形式相对运动。相比于滚珠丝杠，行星滚柱丝杠融合了行星副和螺纹副特点，滚柱与丝杠、滚柱与螺母之间的螺纹同时啮合，接触点多，相对承载和稳定性更好，可在长期无润滑条件下，数倍甚至十数倍以上额定载荷下高可靠性正常运行。随着高端市场对传动部件的精度、承载、寿命及体积等性能追求极致的愿望，迫切需要开发一种新型行星滚柱丝杠，在保持体积不变的情况下，减少磨损量，提升其承载力及使用寿命，以满足用户要求。


技术实现要素：

3.本发明解决的技术问题是：针对目前现有技术中，行星滚柱丝杠副承载力受限、丝杠副效率较低、寿命较短的问题，提出了一种曲面牙型形廓行星滚柱丝杠的优化设计方法。
4.本发明解决上述技术问题是通过如下技术方案予以实现的：
5.一种曲面牙型形廓行星滚柱丝杠的优化设计方法，步骤如下：
6.(1)建立初始坐标系o-xyz、母线坐标系o-xy’z’，于初始坐标系中确定螺旋线г的表达式具体为：
[0007][0008]
式中，r——旋转半径，p——导程，为旋转参数p0；
[0009]
(2)根据螺旋线г的表达式，确定沿垂直螺旋线г任意一点处切线方向截面为螺旋面法截面xoz’，并根据螺旋线г的旋转半径r、导程p，作为螺旋面的中半径r、导程p，确定螺旋面母线的表达式；
[0010]
(3)确定丝杠、滚柱、螺母对应母线类型，并构建各零件下表面对应母线于母线坐标系o-xy’z’，的参数表达式；
[0011]
(4)将丝杠、滚柱、螺母对应母线绕母线坐标系o-xy’z’的x轴旋转螺旋升角α后，获取螺旋面法截面于初始坐标系o-xyz中的表达式；
[0012]
(5)将丝杠、滚柱、螺母对应母线绕母线坐标系o-xy’z’的z轴旋转θ角度后，于z轴
上施加p0·
θ，获取螺旋面法截面任意一点r的矢量于初始坐标系o-xyz中关于曲面参数(u，θ)的表达式，确定螺旋面下、上表面的曲面空间；
[0013]
(6)确定步骤(5)所得曲面空间的微分几何第一类基本量及第二基本量，确定螺旋面对应参数；
[0014]
(7)确定与螺旋面基本量有关的曲面参数，根据hertz接触理论，计算主曲率、主方向夹角、接触椭圆偏心率、椭圆面积，并确定与凹面丝杠牙型形廓有关的结构参数，通过对结构参数进行修正完成对凹面丝杠牙型形廓的结构优化。
[0015]
所述步骤(2)中，初始坐标系o-xyz、母线坐标系o-xy’z’、螺旋面法截面xoz’中，y’为螺旋线的切线方向，z’方向与z方向夹角为螺旋升角螺旋面法截面xoz’的平面曲线即为螺旋面母线，在丝杠小径至丝杠大径的取值范围内单调递增或递减。
[0016]
所述步骤(2)中，螺旋面母线的表达式具体为：
[0017][0018][0019]
式中，下标1代表螺旋面下表面，下标2代表螺旋面上表面。
[0020]
所述步骤(3)中，丝杠、滚柱、螺母对应母线分别为凹圆弧、凸圆弧、直线，对应母线参数表达式分别为：
[0021]
x方向：
[0022]
丝杠：f
x
＝rs+s
t
·
cos(βs)-s
t
·
cos(βs+us)
[0023]
滚柱：f
x
＝-(rr+r
t
·
sin(ur+βr)-r
t
·
sin(βr))
[0024]
螺母：f
x
＝rn+un·
cos(βn)
[0025]
z方向：
[0026]
丝杠：
[0027]
滚柱：
[0028]
螺母：
[0029]
式中，r为半径，下标s、r、n分别代表丝杠、滚柱和螺母，r
t
是滚柱母线圆弧的半径，s
t
是丝杠母线圆弧的半径，p为丝杠、滚柱和螺母的螺距，丝杠与螺母导程p＝p
·nt
，n
t
为头数，滚柱的导程pr＝p，un为母线上任意一点到中径处的距离，us、ur为母线圆弧上任意一点到中径处的夹角。
[0030]
所述步骤(4)、步骤(5)中，确定初始坐标系o-xyz中绕x轴的旋转矩阵t
x
(α)及绕z轴的旋转矩阵tz(θ)及丝杠、滚柱、螺母对应母线对应表达式，确定任意一点r的矢量于初始
坐标系o-xyz中关于曲面参数(u，θ)的表达式，具体为：
[0031][0032][0033][0034]
式中，r1、r2为螺旋面下、上表面的曲面空间。
[0035]
所述步骤(6)中，螺旋面对应参数具体为：
[0036]
微分几何第一类基本量具体为：
[0037]
包括e＝ru·ru
、f＝ru·rθ
、g＝r
θ
·rθ
，其中：e＝f
x
'(u)2+fz′
′
(u)2[0038]
f＝p0·fz
′
′
(u)
·
cos(α)-(f
z'
(u)
·fx
'(u)-fz′
′
(u)
·fx
(u))
·
sin(α)
[0039]
g＝p
02
+f
x
(u)2+(f
z'
(u)
·
sin(α))2[0040]
式中，f
x
'(u)、fz′
′
(u)分别为f
x
(u)、f
z'
(u)关于u的一阶导数。
[0041]
所述步骤(6)中，微分几何第二类基本量具体为：
[0042]
包括l＝r
uu
·
n、m＝r
uθ
·
n、n＝r
θθ
·
n，其中：
[0043][0044][0045][0046]
式中，f
x
"(u)、f
z'
"(u)分别为f
x
(u)和f
z'
(u)关于u的二阶导数。
[0047]
所述步骤(7)中，所述与曲面丝杠牙型形廓有关的结构参数具体包括牙型角、牙弧半径，通过修正牙型角、牙弧半径改变曲面丝杠牙型形廓的结构，完成优化。
[0048]
本发明与现有技术相比的优点在于：
[0049]
本发明提供的一种曲面牙型形廓行星滚柱丝杠的优化设计方法，通过参数的设置实现行星滚柱丝杠的设计调整，能够保持体积不变的情况下，减少磨损量，提升其承载力及使用寿命，同时优化设计后的行星滚柱丝杠工作效率不受影响，不会降低优化设计后的行星滚柱丝杠的承载性能，提高行星滚柱丝杠副的极限承载力，并提高行星滚柱丝杠副的使
用寿命。
附图说明
[0050]
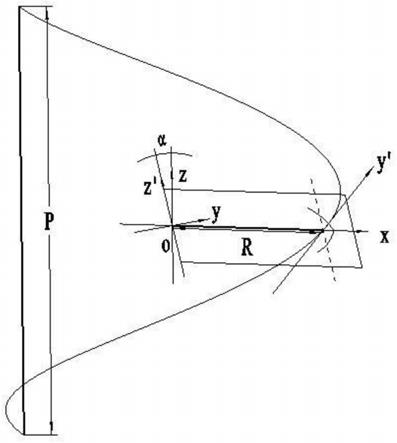
图1为发明提供的螺旋线于初始坐标系及母线坐标系中示意图；
[0051]
图2为发明提供的丝杠、滚柱、螺母对应母线示意图；
具体实施方式
[0052]
一种曲面牙型形廓行星滚柱丝杠的优化设计方法，能够在保持体积不变的情况下，减少磨损量，提升其承载力及使用寿命，具体优化步骤如下：
[0053]
(1)建立初始坐标系o-xyz、母线坐标系o-xy’z’，于初始坐标系中确定螺旋线г的表达式具体为：
[0054][0055]
式中，r——旋转半径，p——导程，为旋转参数p0；
[0056]
(2)根据螺旋线г的表达式，确定沿垂直螺旋线г任意一点处切线方向截面为螺旋面法截面xoz’，并根据螺旋线г的旋转半径r、导程p，作为螺旋面的中半径r、导程p，确定螺旋面母线的表达式；
[0057]
(3)确定丝杠、滚柱、螺母对应母线类型，并构建各零件下表面对应母线于母线坐标系o-xy’z’，的参数表达式；
[0058]
(4)将丝杠、滚柱、螺母对应母线绕母线坐标系o-xy’z’的x轴旋转螺旋升角α后，获取螺旋面法截面于初始坐标系o-xyz中的表达式；
[0059]
(5)将丝杠、滚柱、螺母对应母线绕母线坐标系o-xy’z’的z轴旋转θ角度后，于z轴上施加p0·
θ，获取螺旋面法截面任意一点r的矢量于初始坐标系o-xyz中关于曲面参数(u，θ)的表达式，确定螺旋面下、上表面的曲面空间；
[0060]
(6)确定步骤(5)所得曲面空间的微分几何第一类基本量及第二基本量，确定螺旋面对应参数；
[0061]
(7)确定与螺旋面基本量有关的曲面参数，根据hertz接触理论，计算主曲率、主方向夹角、接触椭圆偏心率、椭圆面积，并确定与凹面丝杠牙型形廓有关的结构参数，通过对结构参数进行修正完成对凹面丝杠牙型形廓的结构优化。
[0062]
步骤(2)中，初始坐标系o-xyz、母线坐标系o-xy’z’、螺旋面法截面xoz’中，y’为螺旋线的切线方向，z’方向与z方向夹角为螺旋升角螺旋面法截面xoz’的平面曲线即为螺旋面母线，在丝杠小径至丝杠大径的取值范围内单调递增或递减；
[0063]
步骤(2)中，螺旋面母线的表达式具体为：
[0064][0065][0066]
式中，下标1代表螺旋面下表面，下标2代表螺旋面上表面；
[0067]
步骤(3)中，丝杠、滚柱、螺母对应母线分别为凹圆弧、凸圆弧、直线，对应母线参数表达式分别为：
[0068]
x方向：
[0069]
丝杠：f
x
＝rs+s
t
·
cos(βs)-s
t
·
cos(βs+us)
[0070]
滚柱：f
x
＝-(rr+r
t
·
sin(ur+βr)-r
t
·
sin(βr))
[0071]
螺母：f
x
＝rn+un·
cos(βn)
[0072]
z方向：
[0073]
丝杠：
[0074]
滚柱：
[0075]
螺母：
[0076]
式中，r为半径，下标s、r、n分别代表丝杠、滚柱和螺母，r
t
是滚柱母线圆弧的半径，s
t
是丝杠母线圆弧的半径，p为丝杠、滚柱和螺母的螺距，丝杠与螺母导程p＝p
·nt
，n
t
为头数，滚柱的导程pr＝p，un为母线上任意一点到中径处的距离，us、ur为母线圆弧上任意一点到中径处的夹角；
[0077]
步骤(4)、步骤(5)中，确定初始坐标系o-xyz中绕x轴的旋转矩阵t
x
(α)及绕z轴的旋转矩阵tz(θ)及丝杠、滚柱、螺母对应母线对应表达式，确定任意一点r的矢量于初始坐标系o-xyz中关于曲面参数(u，θ)的表达式，具体为：
[0078][0079]
[0080][0081]
式中，r1、r2为螺旋面下、上表面的曲面空间；
[0082]
步骤(6)中，螺旋面对应参数具体为：
[0083]
微分几何第一类基本量具体为：
[0084]
包括e＝ru·ru
、f＝ru·rθ
、g＝r
θ
·rθ
，其中：
[0085]
e＝f
x
'(u)2+fz′
′
(u)2[0086]
f＝p0·fz
′
′
(u)
·
cos(α)-(f
z'
(u)
·fx
'(u)-fz′
′
(u)
·fx
(u))
·
sin(α)
[0087]
g＝p
02
+f
x
(u)2+(f
z'
(u)
·
sin(α))2[0088]
式中，f
x
'(u)、fz′
′
(u)分别为f
x
(u)、f
z'
(u)关于u的一阶导数；
[0089]
步骤(6)中，微分几何第二类基本量具体为：
[0090]
包括l＝r
uu
·
n、m＝r
uθ
·
n、n＝r
θθ
·
n，其中：
[0091][0092][0093][0094]
式中，f
x
"(u)、f
z'
"(u)分别为f
x
(u)和f
z'
(u)关于u的二阶导数；
[0095]
步骤(7)中，所述与曲面丝杠牙型形廓有关的结构参数具体包括牙型角、牙弧半径，通过修正牙型角、牙弧半径改变曲面丝杠牙型形廓的结构，完成优化。
[0096]
下面根据具体实施例进行进一步说明：
[0097]
在当前实施例中，丝杠、滚柱、螺母由母线绕螺旋线旋转生成，在坐标系o-xyz中作螺旋线г，其中，螺旋线г的表达式具体为：
[0098][0099]
式中，r——旋转半径，p——导程，为旋转参数p0；
[0100]
建立初始坐标系o-xyz和母线坐标系o-xy’z’，沿垂直螺旋线某一点处切线方向作螺旋面的截面，为螺旋面的法截面xoz’，y’为螺旋线的切线方向，z’与z的夹角为螺旋升角
截取的平面曲线即为螺旋面的母线，通常在取值范围内单调递增或递减。螺旋线的旋转半径r和导程p分别为螺旋面的中半径r和导程p。螺旋面的母线可用以u为自变量的函数表达，对关于x轴对称的上下母线，有：
[0101][0102][0103]
其中，下标1代表下表面，下标2代表上表面，几何关系如图1所示。
[0104]
如图1所示，丝杠、滚柱与螺母的母线分别为凹圆弧、凸圆弧和直线。其中r为半径，下标s、r、n分别代表丝杠、滚柱和螺母；r
t
是滚柱母线圆弧的半径，s
t
是丝杠母线圆弧的半径；p为丝杠、滚柱和螺母的螺距。丝杠与螺母导程p＝p
·nt
，n
t
为头数，滚柱的导程pr＝p。表1给出了各零件下表面的母线在坐标系o
’‑
xy’z’的参数表达形式。以半径处u＝0，图所示方向为u的正方向，变量u有明确的几何意义，其中un表示母线上任意一点到中径处的距离，us和ur表示母线圆弧上任意一点到中径处的夹角；
[0105]
表1母线参数表达式
[0106][0107]
将丝杠、滚柱、螺母对应母线所在平面绕x轴旋转螺旋升角α后，得到法截面在坐标系o-xyz的方程；母线绕z轴旋转θ角度后在z轴加上p0·
θ，得到螺旋面一点r的矢量在坐标系o-xyz关于曲面参数的(u，θ)的表达式。其中，绕x轴的旋转矩阵t
x
(α)和绕z轴的旋转矩阵tz(θ)，通过旋转矩阵与上表中所示的母线参数表达式，确定r的矢量在坐标系o-xyz关于曲面参数的(u，θ)的表达式，具体为：
[0108]
[0109][0110][0111]
式中，r1、r2为螺旋面下、上表面的曲面空间；
[0112]
根据微分几何，曲面的第一类基本量e＝ru·ru
、f＝ru·rθ
、g＝r
θ
·rθ
，则对螺旋面有：
[0113]
e＝f
x
'(u)2+fz′
′
(u)2[0114]
f＝p0·fz
′
′
(u)
·
cos(α)-(f
z'
(u)
·fx
'(u)-fz′
′
(u)
·fx
(u))
·
sin(α)
[0115]
g＝p
02
+f
x
(u)2+(f
z'
(u)
·
sin(α))2[0116]
式中，f
x
'(u)、fz′
′
(u)分别为f
x
(u)、f
z'
(u)关于u的一阶导数；
[0117]
同时，确定曲面的第二类基本量为l＝r
uu
·
n、m＝r
uθ
·
n、n＝r
θθ
·
n。对螺旋面有：
[0118][0119][0120][0121]
时，f
x
"(u)和f
z'
"(u)分别是f
x
(u)和f
z'
(u)关于u的二阶导数。可以看出，螺旋面的第一类基本量与第二类基本量都与θ无关。
[0122]
依据hertz接触理论，两点接触的弹性体在受到外加载荷的情况下，接触点处发生弹性变形变为椭圆区域。在确定弹性体材料及法向接触载荷后，接触椭圆长短半轴可通过弹性体接触点处的主曲率函数求出，主曲率可由第一类基本量和第二类基本量求出，表2给出了在相同材料和法向载荷下，凹面丝杠和直线丝杠分别与同一滚柱接触后的接触点主曲率、主方向夹角、接触椭圆偏心率和椭圆面积，其中，凹面丝杠的牙弧半径分别为50和10。
[0123]
表2凹面丝杠与平面丝杠参数对比
[0124][0125]
由上表可知，凹面丝杠的接触椭圆面积均大于平面丝杠，当母线的牙弧半径减少至10时，凹面丝杠的接触椭圆面积比直线丝杠增加33％。
[0126]
通过上述分析可知，忽略主方向夹角带来的偏差，则接触点及接触椭圆的面积仅与母线的形状相关。由于现有设计中，滚柱均为同一母线，且绕主丝杠周向排布，因此在主丝杠对应的接触点必然为同一点，即主丝杠的螺纹表面仅一条螺纹接触曲线时刻发生接触，而其余的点没有参加接触，长时工作后，该条螺纹曲线上的各个接触点将有可能产生疲劳点蚀，降低丝杠精度，甚至缩短丝杠寿命。对滚柱螺纹表面修形，使各滚柱与丝杠的接触点发生变化，即可降低主丝杠接触线应力循环次数，延长丝杠的寿命。表3给出了针对15
×
4这种规格中各滚柱牙型角及牙弧半径的取值。考虑到高速运转时，不同接触点使转动惯量发生改变，进而引起振颤，因此在周向排布10个滚柱，分为5类，每类两个，对称放置。
[0127]
表3滚柱牙型角及牙弧半径取值
[0128]
滚柱编号牙型角牙弧半径143
°
1244
°
2345
°
3446
°
3.5547
°
1.5
[0129]
通过上述优化方法，计算了凹面圆弧牙型形廓主丝杠与凸面圆弧牙型形廓滚柱在接触点处的接触面积，对比平面牙型形廓主丝杠与凸面圆弧牙型形廓滚柱在接触点处的面积增加了33％，减少了接触点处的最大接触应力。在材料极限应力一定的情况下，提高了行星滚柱丝杠副的极限承载力。
[0130]
通过上述优化方法，调整滚柱螺纹法截面的牙型角与牙弧半径，使每个滚柱与主丝杠接触在不同螺旋线上，相对现有设计方法，减少了主丝杠螺纹表面的应力循环次数。在材料接触疲劳极限一定的情况下，提高了行星滚柱丝杠副的使用寿命。
[0131]
本发明虽然已以较佳实施例公开如上，但其并不是用来限定本发明，任何本领域技术人员在不脱离本发明的精神和范围内，都可以利用上述揭示的方法和技术内容对本发
明技术方案做出可能的变动和修改，因此，凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化及修饰，均属于本发明技术方案的保护范围。
[0132]
本发明说明书中未作详细描述的内容属于本领域技术人员的公知技术。