一种无保持球轴承减少滚动体碰撞的方法

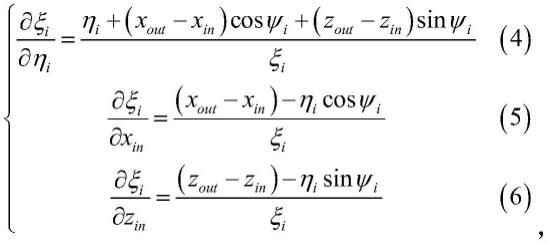
1.本发明涉及无保持架球轴承技术领域，尤其是一种无保持球轴承减少滚动体碰撞的方法。


背景技术：

2.近年来，随着航空发动机、电主轴以及高精度机床的发展，对滚动轴承的转速要求越来越高，陶瓷轴承以其较高的极限转速和耐高温性能等优势越来越受到人们的重视。现阶段工程中应用的主要是混合陶瓷轴承，即滚动体为陶瓷材料，内、外圈仍采用钢制材料，并含有保持架，保持架的作用是为了减少滚动体直接接触时产生的阻力。然而，在高速运转情况下，保持架与滚动体和套圈之间的摩擦也会产生不可忽视的阻力，致使轴承发热，从而限制了轴承的极限转速。为了避免保持架所带来的摩擦阻力，实现轴承的高速或超高速运行，近年来国外出现了无保持架陶瓷球轴承。在没有保持架而滚动体相互接触的轴承中，会存在下列问题：(1)由于相邻滚动体间凸起的相互接触而产生的高接触面压力；(2)由于滚动体的自转而产生的相互反向的快速滑动速度，由于接触点的油膜破裂而容易产生摩擦、磨损、烧结等问题。因此，本文在无保持架球轴承的外圈设置一个或多个离散槽，达到避免滚动体相互接触的目的


技术实现要素：

3.本发明要解决的技术问题是：为了解决减少现有无保持架滚动体碰撞的问题，本发明提供了一种无保持球轴承减少滚动体碰撞的方法，通过对无保持架球轴承外沟道内表面进行离散槽设计，改变滚动体的动能使相邻滚动体产生间距，达到减少滚动体间碰撞产生摩擦的目的。
4.本发明解决其技术问题所采用的技术方案是：
5.一种无保持球轴承减少滚动体碰撞的方法，包括如下步骤：
6.1)基于能量分析建立ηi(i＝1,2,...,z)、x
in
、z
in
的运动微分方程，具体为：
[0007][0008]
其中：
[0009][0010]
式中，mb为滚动体质量，ηi为滚动体径向位置，其中，ηi(i＝1,2,...,z)，z为滚动体的个数，g取9.8n/kg，ψi(ψi≥0)为第i个滚动体的位置角，k
in
为第i个滚动体与内圈之间的接触刚度，k
out
为第i个滚动体与外圈之间的接触刚度，r
in
为无保持架球轴承内圈外滚道半径，r
out
为无保持架球轴承外圈内滚道半径，rb为滚动体半径，ξi为滚动体与内圈间弹簧的变形，m
in
为内圈质量，x
in
为内圈沿x轴的位移，k为，z
in
为内圈沿z轴的位移，fr为作用在轴承系统上的径向力，x
out
为外圈沿x轴的位移，z
out
为外圈沿z轴的位移；
[0011]
2)将式(4)、(5)、(6)分别代入式(1)、(2)、(3)中，并采用 runge-kutta法求解ηi(i＝1,2,...,z)、x
in
、z
in
运动微分方程，求得内圈滚动体的速度与位移；
[0012]
3)根据内圈滚动体的速度与位移优化离散槽参数。
[0013]
具体地，11)将无保持架球轴承看作弹簧-质量系统，如图1所示，将滚动体内、外圈接触力看作非线性接触弹簧，基于赫兹弹性接触变形理论求得非线性弹簧的刚度，因离散槽参数导致的滚动体质心径向位移直接影响轴承各部件动能与势能，利用拉格朗日方程和无保持架球轴承各部件的动能和势能表达式，建立了一组独立广义坐标系的拉格朗日方程：
[0014][0015]
式中：t、v、p、f分别为动能、势能、广义自由度坐标矢量、广义接触力矢量；
[0016]
12)假设外圈固定不动，无保持架球轴承中的总动能是滚动体动能与内圈动能之和，其方程为：
[0017][0018]
式中：t
roller
、t
in
、t
out
分别表示滚动体动能、内圈动能和外圈动能；
[0019]
13)势能的变化是由离散槽的结构与滚动体随滚道的变形所引起的，在轴承系统坐标系中，以平面x0oy0为水平面进行势能计算，即选取轴承中心为重力势能零位，无保持架球轴承中的总势能是滚动体势能、内圈势能、外圈势能以及弹簧势能之和，其方程为：
[0020][0021]
式中：v
roller
、v
in
、v
out
分别表示滚动体势能、内圈势能和外圈势能，v
t
是由于滚动体与内、外圈之间的非线性弹簧接触而产生的势能；
[0022]
将式(8)、(9)代入式(7)中，并分别对ηi(i＝1,2,...,z)、x
in
、z
in
求导，可得ηi(i＝1,2,...,z)、x
in
、z
in
的运动微分方程。
[0023]
具体地，为了建立内、外圈的动能、势能方程，建立了无保持架球轴承的弹簧-质量模型位移分析图，如图2所示，假设轴承外圈中心固定不变且外圈为刚体，则可推导出ω
out
＝0，无保持架球轴承外圈动能表达式为：
[0024][0025]
无保持架球轴承外圈势能表达式为：
[0026][0027]
式中，m
out
表示外圈质量；
[0028]
除了接触中的局部变形外，内圈被认为是刚体，在x0oz0中计算了内圈绕轴承中心的动能，内圈动能表达式为：
[0029][0030]
其中：m
in
表示内圈质量，i
in
表示内圈转动惯量，是通过质量和回转半径计算得到的一个具体数值，ω
in
表示内圈转速，表示在平面x0oz0中内圈中心相对轴承中心坐标(0,0)的位移变化，即
[0031]
假设轴承外圈中心是固定不变，已知内圈中心相对外圈中心的位移变化则可以表示为：
[0032][0033]
也可以表示为：
[0034][0035]
轴承外圈中心固定不变，故
[0036][0037]
因此，将式(24)化简为：
[0038][0039]
无保持架球轴承内圈势能表达式为：
[0040]vin
＝m
in
g(z
out-z
in_out
)
ꢀꢀꢀ
(14)
[0041]
式中：z
in_out
表示内圈中心相对于外圈中心的相对坐标；
[0042]
轴承中z个滚动体产生的动能总和为：
[0043][0044]
滚动体质心位置相对外圈中心的位置是确定的，因此，第i个滚动体的动能为：
[0045][0046]
式中，mb为滚动体质量，表示第i个滚动体质心位移矢量，其表达式为：
[0047][0048]
结合对时间进行微分，可得：
[0049][0050]
由于和故
[0051][0052]
第i个滚动体的动能表达式为：
[0053][0054]
假设没有滑移，因此外圈和球的相对过渡速度必须相同且反向，因此，第i 个滚动体与外圈的接触方程为：
[0055][0056]
其中，
[0057][0058]
由于外圈是静止的，故
[0059][0060]
综上，轴承中z个滚动体产生的动能方程为：
[0061][0062]
式中：m为滚动体质量，ro为外圈与滚动体接触点的半径，ii为内圈转动惯量；式中：m
in
表示内圈质量，i
in
表示内圈转动惯量，ω
in
表示内圈转速；
[0063]
轴承中z个滚动体产生的势能方程为：
[0064]
[0065]
式中：z
out
表示外圈中心的z轴坐标；
[0066]
根据图2中无保持架球轴承弹簧-质量模型可知，离散槽导致的滚动体质心径向位移m
lsc
直接影响滚动体动能方程与势能方程中的滚动体径向位置ηi，其关系式为：
[0067][0068]
将滚动体与内、外圈之间的接触视为非线性弹簧，其刚度由赫兹弹性理论得到，由弹簧接触变形引起的势能的表达式为：
[0069][0070]
式中：k
in
为由于滚动体与内圈间赫兹接触效应引起的非线性刚度，k
out
为由于滚动体与外圈间赫兹接触效应引起的非线性刚度，δ
in
为第i个滚动体与内圈接触变形，δ
out
为第i个滚动体与外圈接触变形；若(r
in
+rb)＞ξi，则滚动体与内圈间弹簧会发生压缩或恢复力的作用，δ
in
＝[(r
in
+rb)-ξi]，若(r
in
+rb)≤ξi，则δ
in
＝0；若r
out
＜(ηi+rb)，则滚动体与外圈间弹簧会发生压缩或恢复力的作用，δ
out
＝[r
out-(ηi+rb)]；若r
out
≥(ηi+rb)，则δ
out
＝0。
[0071]
具体地，所述第i个滚动体与内圈之间的接触刚度：
[0072][0073]
所述第i个滚动体与外圈之间的接触刚度：
[0074][0075]
其中，r
ni
为第i个滚动滚动体与内圈的有效接触半径、r
wi
为第i个滚动滚动体与外圈的有效接触半径，r
out
为无保持架球轴承外圈内滚道半径，l
10
、l
20
分别为滚动体与内、外圈接触弹簧模型平衡的弹簧长度。
[0076]
具体地，当滚动体位于离散槽中时，即滚动体脱离了内圈，故此时ξi＝0。由图2可知，ξi的表达式为：
[0077][0078]
所述滚动体与内圈间弹簧的变形为：
[0079][0080]
式中，ψi(ψi≥0)为第i个滚动体的位置角，x
in
为内圈沿x轴的位移，z
in
为内圈沿z轴的位移，x
out
为外圈沿x轴的位移，z
out
为外圈沿z轴的位移；
[0081]
则ξi对ηi(i＝1,2,...,z)，x
in
，z
in
分别求偏导，可得：
[0082][0083]
根据farhang k与mehra k的研究可知，第i个滚动体的位置角为：
[0084][0085]
其中：
[0086]
式中：ωi为内圈转速，rb为滚动体半径，αi为滚动体与内圈接触角，dm为无保持架球轴承中节圆直径，以轴承中心为圆心，以常规外圈滚道的滚动体质心到轴承中心距离为半径的圆，称为无保持架球轴承的节圆，z为滚动体个数，t为时间，ψ0为滚动体初始位置角，一般情况下ψ0＝0。
[0087]
本发明的有益效果是：本发明提供的一种无保持球轴承减少滚动体碰撞的方法，无保持架球轴承为了避免了滚动体与滚动之间的碰撞摩擦，提出了一种无保持架球轴承减少碰撞的方法，本文提出在无保持架球轴承外圈滚道设置离散槽，通过改变滚动体的动能使相邻滚动体产生间距，达到减少滚动体间碰撞的目的。
附图说明
[0088]
图1：滚动体与内外圈接触关系分析图；
[0089]
图2：无保持架球轴承的弹簧-质量模型位移分析图；
[0090]
图3：椭圆形离散槽示意图；
[0091]
图4：无保持架球轴承运动方程求解分析图
[0092]
图5：离散槽位于承载区的内圈相图；
[0093]
图6：椭圆形离散槽位于非承载区的内圈相图；
[0094]
图7：两个椭圆形离散槽的内圈相图；
[0095]
图8：三个椭圆形离散槽的内圈相图；
[0096]
图9：位于常规外圈滚道的滚动体速度-位移相图；
[0097]
图10：位于椭圆形离散槽的滚动体速度-位移相图；
[0098]
图11：位于承载区的一个椭圆形离散槽轴承内圈庞加莱图。
具体实施方式
[0099]
现在对本发明作进一步详细的说明。
[0100]
本发明的一种无保持球轴承减少滚动体碰撞的方法，包括如下步骤：
[0101]
1)基于能量分析建立ηi(i＝1,2,...,z)、x
in
、z
in
的运动微分方程，具体为：
[0102][0103]
其中：
[0104][0105]
式中，mb为滚动体质量，ηi为滚动体径向位置，其中，ηi(i＝1,2,...,z)，z为滚动体的个数，g取值9.8n/kg，ψi(ψi≥0)为第i个滚动体的位置角，k
in
为第i 个滚动体与内圈之间的接触刚度，k
out
为第i个滚动体与外圈之间的接触刚度，r
in
为无保持架球轴承内圈外滚道半径，r
out
为无保持架球轴承外圈内滚道半径，rb为滚动体半径，ξi为滚动体与内圈间弹簧的变形，m
in
为内圈质量，x
in
为内圈沿x 轴的位移，k为，z
in
为内圈沿z轴的位移，fr为作用在轴承系统上的径向力，x
out
为外圈沿x轴的位移，z
out
为外圈沿z轴的位移；
[0106]
2)将式(4)、(5)、(6)分别代入式(1)、(2)、(3)中，并采用 runge-kutta法求解ηi(i＝1,2,...,z)、x
in
、z
in
运动微分方程，求得内圈滚动体的速度与位移；
[0107]
3)根据内圈滚动体的速度与位移优化离散槽参数。
[0108]
为了方便演示，将槽的形状参数定义为具有代表性的对称性形状椭圆形，采用四阶runge-kutta法对无保持架球轴承运动微分方程(1)、(2)、(3) 进行数值求解，得到具有不同离散槽参数的轴承内圈中心x轴和z轴两个方向、滚动体径向速度与位移。其中，无保持架球轴承模型拟选取的参数值如表1-1 所示：
[0109]
表1-1无保持架球轴承模型参数
[0110][0111]
为了便于平面投影形状不同的离散槽进行对比分析，皆取m
lsc
的最大值为 1mm，椭圆形离散槽(如图3所示)所导致的滚动体质心径向位移是随时间不断变化的，为了区分不同形状离散槽的细微差别，椭圆形离散槽所导致的某一位置滚动体径向位移值分别取0.8mm，同时，离散槽位于承载区时，取内圈中心初始位置为(0,0)；离散槽位于承载区时，取内圈中心初始位置为(0,0.5)，求解时间为0.1s。
[0112]
通过对比分析离散槽参数的无保持架球轴承滚动体质心及内圈中心的速度
‑ꢀ
位移相图，得到离散槽的位置及个数对轴承内部各部件运动稳定性的影响，具体求解方法及程序求解流程图，如图4所示。
[0113]
如图5所示，无保持架球轴承内圈中心的速度-位移相图，也为封闭的且有一定宽度的椭圆形曲线，内圈中心沿x轴方向的速度范围为
ꢀ‑
1.5
×
104～1.5
×
104μm/s，位移范围为0～1.9μm，沿z轴方向的速度范围为
ꢀ‑
6000～6000μm/s，位移范围为0.5～1.38μm。
[0114]
发现离散槽的无保持架球轴承x轴与z轴方向速度-位移相图为封闭且有一定宽度的椭圆形曲线，表明了球轴承内圈运动为稳定的拟周期运动。图5中，x 轴方向的速度-位移相图几乎一样，然而，观察z轴方向的速度-位移相图发现，椭圆形离散槽的无保持架球轴承当离散槽的个数为一个且位于承载区时，离散槽使无保持架球轴承内圈振动小，运动稳定性好。
[0115]
当无保持架球轴承系统具有一个较长周期时，仅通过相图的轨迹判断系统是周期运动还是混沌运动是比较困难的，故采用一个更加有效的方法进行判别，即庞加莱截面法。初始参数保持不变，将求解时间延长为1s，根据内圈转速为 3000r/min，内圈运动轨迹与某个截面应有50个交点，故所绘制的庞加莱截面上有50个点。如图11，通过庞加莱截面法判别具有一个位于承载区离散槽的无保持架球轴承内圈z轴方向的运动是周期运动还是混沌运动。
[0116]
若庞加莱截面图上为单个点或有限个集中的点，则内圈运动为单周期运动或倍周期运动；若庞加莱截面图上所显示的点紧密地分布在一条封闭曲线上，则内圈运动为拟周期运动；若庞加莱截面图上有无限个点且没有规律，则内圈运动为混沌运动。根据图11中庞加莱截面图的特点可知，无保持架球轴承内圈沿z轴方向运动为拟周期运动。观察图11中，
可以发现无保持架球轴承中具有一个位于承载区的椭圆形离散槽时，内圈运转精度高，稳定强。
[0117]
当离散槽的个数为一个且位于非承载区时，离散槽平面投影的形状对内圈运动的影响，离散槽的无保持架球轴承内圈中心轴方向位移范围略小，当离散槽的个数为一个且位于非承载区时，椭圆形离散槽使无保持架球轴承内圈振动更小，运动稳定性更好。
[0118]
离散槽位于承载区与非承载区时，承受径向载荷的滚动体数目不同，离散槽的位置必然对无保持架球轴承内圈轴方向运动产生不同的影响，如图6为无保持架球轴承中具有一个位于非承载区的离散槽，内圈中心轴方向的速度-位移相图。
[0119]
如图7为无保持架球轴承中具有两个位置角间隔为π的离散槽时，内圈中心在x轴和z轴两个方向的速度-位移相图，其中，一个离散槽位于承载区，另一个离散槽位于非承载区，由图可知，无保持架球轴承内圈中心x轴方向与z轴方向速度-位移相图皆为封闭的且有一定宽度的椭圆形曲线，z轴方向的曲线宽度略大于x轴方向的曲线宽度。同时，内圈中心沿x轴方向的速度范围为
ꢀ‑
1.5
×
104～1.5
×
104μm/s，位移范围为0～2μm，沿z轴方向的速度范围为
ꢀ‑
7000～7000μm/s，位移范围为0.5～1.45μm。
[0120]
离散槽个数为两个且一个位于承载区、另一个位于非承载区时，无保持架球轴承内圈中心在x轴和z轴两个方向的速度-位移相图，它们都为封闭的曲线，故内圈运动都具有明显的周期性，无保持架球轴承内圈振动小，运动稳定性好。
[0121]
如图8所示为无保持架球轴承中具有三个椭圆形离散槽时，内圈中心的速度-位移相图。由图可知，无保持架球轴承内圈中心x轴方向与z轴方向速度-位移相图皆为封闭的且有一定宽度的椭圆形曲线，z轴方向的曲线宽度略大于x轴方向的曲线宽度。同时，内圈中心沿x轴方向的速度范围为-1.5
×
104～1.5
×
104μm/s，位移范围为0～2.3μm，沿z轴方向的速度范围为
ꢀ‑1×
104～1
×
104μm/s，位移范围为0.5～1.7μm。
[0122]
离散槽个数为三个且一个位于承载区、两个位于非承载区时，无保持架球轴承内圈中心沿x轴方向的速度-位移相图为封闭的圆形曲线，沿z轴方向的速度
ꢀ‑
位移相图为封闭且存在一定宽度的椭圆形曲线。
[0123]
关于离散槽位置的优选，当离散槽个数为一个，离散槽位于承载区时比其位于非承载区时，内圈沿z轴方向速度与位移变化范围更小。故存在一个位于承载区的离散槽时，无保持架球轴承内圈运动周期性更强，运动更稳定。
[0124]
滚动体位于常规滚道和椭圆形离散槽时质心径向位移与速度范围也不相同，如图9和图10所示，为滚动体分别位于常规滚道和椭圆形离散槽时，滚动体质心的径向位移与速度相图。滚动体位于常规外圈滚道时，如图9所示，无保持架球轴承中滚动体速度-位移的相图为多条封闭椭圆形曲线，速度范围为
ꢀ‑8×
107～8
×
107μm/s，位移范围为-100～100μm。滚动体位于椭圆形离散槽时，如图10所示，无保持架球轴承中滚动体速度-位移的相图为多条封闭椭圆形曲线，速度范围为-3
×
107～3
×
107μm/s，位移范围为-70～60μm。
[0125]
滚动体径向位移-速度相图可知，相图不重复且充满相空间，故滚动体的运动为混沌运动。相图中，滚动体位于离散槽比位于常规外圈滚道速度变化范围小很多，原因为滚动体从常规外圈滚道进入离散槽中，脱离内圈，动能减小。根据图中滚动体径向位移与速度范围大小的对比可知，椭圆形离散槽有利于抑制滚动体径向方向的混沌运动。
[0126]
无保持架球轴承具有一个、两个离散槽时，内圈沿x轴方向速度变化范围一致，都
略小于具有三个离散槽时内圈沿x轴方向速度的变化范围。无保持架球轴承内圈沿x轴方向位移变化范围、沿z轴方向速度与位移变化范围，也随着离散槽个数的增多而增大。因此，离散槽个数理论优选结果也为一个。
[0127]
无保持架球轴承中存在一个位于承载区的离散槽时，内圈运动精度更高，稳定性更强。
[0128]
以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。