一种基于非高斯非圆信号特性的稳健自适应波束形成方法

1.本发明涉及阵列信号处理领域中波束形成研究领域，尤其涉及一种基于非高斯非圆信号特性的稳健自适应波束形成方法。


背景技术：

2.传统比较著名的稳健自适应波束形成算法有：对角加载类算法、基于特征子空间算法、基于不确定集算法等，但是在实际中，存在着各种各样的误差，导致这几类波束形成算法的性能有较为明显的下降。近年来，基于协方差矩阵重构的算法受到了广泛的关注，并且取得了优于传统算法的性能。然而，该类算法是一种通用算法，并未考虑到利用信号的特性来进一步提高波束形成器的性能，因此该类算法的性能始终差于理论最优的capon波束形成器或最小方差无失真响应(minimum variance distortionless response，mvdr)波束形成器的性能。同时，该类算法需要构造凸优化问题完成对期望信号导向矢量的估计，计算复杂度较大。此外，人们对波束形成器的性能要求越来越高，而大多数利用信号的特性提升波束形成器性能的算法依旧需要进行凸优化问题的求解，仍存在着较高计算复杂度的问题，并且性能有限。鉴于此，有必要利用信号特性研究新的稳健自适应波束形成算法，提高波束形成器在实际应用中的性能。


技术实现要素：

3.本发明的目的是提供一种基于非高斯非圆信号特性的稳健自适应波束形成方法，通过对信号源导向矢量以及非圆系数的估计，进一步提高波束形成器在实际阵列误差存在条件下的性能。
4.本发明的目的是通过以下技术方案实现的：一种基于非高斯非圆信号特性的稳健自适应波束形成方法，包括：
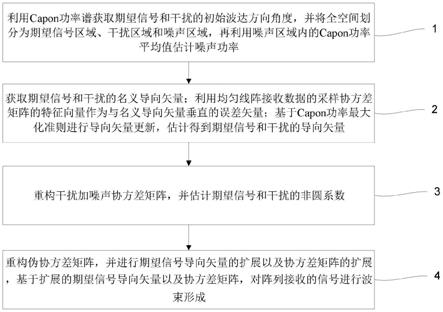
5.步骤1、利用capon功率谱获取期望信号和干扰的初始波达方向角度，并将全空间划分为期望信号区域、干扰区域和噪声区域，再利用噪声区域内的capon功率平均值估计噪声功率；
6.步骤2、根据已知的均匀线阵阵列结构和步骤1中的初始波达方向角度，获取期望信号和干扰的名义导向矢量；利用均匀线阵接收数据的采样协方差矩阵的特征向量作为与名义导向矢量垂直的误差矢量；基于capon功率最大化准则进行导向矢量更新，估计得到期望信号和干扰的导向矢量；
7.步骤3、利用步骤1中估计的噪声功率以及步骤2中估计的期望信号和干扰的导向矢量重构干扰加噪声协方差矩阵，并估计期望信号和干扰的非圆系数；
8.步骤4、基于步骤2中估计的导向矢量以及步骤3中估计的非圆系数，重构伪协方差矩阵，并进行期望信号导向矢量的扩展以及协方差矩阵的扩展，基于扩展的期望信号导向矢量以及协方差矩阵，对阵列接收的信号进行波束形成。
9.所述步骤1具体包括：
10.(11)利用capon功率谱获取期望信号和干扰的初始波达方向角度，并将全空间划分为期望信号区域、干扰区域和噪声区域：
11.对于角度θ来说，其对应的capon功率为：
12.θ∈θ
13.其中，表示角度θ对应的名义导向矢量，m表示阵元数，t表示矩阵或者向量的转置运算。λ＝v/f为窄带信号源的波长，v表示信号源的传播速度，f表示信号源的频率。表示阵列接收数据的采样协方差矩阵，k表示快拍数，x(k)表示阵列在时刻k接收的数据，h表示矩阵或者向量的共轭转置运算，θ表示全空间，计算全空间的capon功率谱，通过谱峰搜索，获取期望信号和干扰的初始波达方向角度，记为l为期望信号和干扰的总数；
14.依据估计得到的初始波达方向角度，将全空间划分为期望信号区域干扰区域θi＝θ1∪θ2∪
…
∪θ
l-1
和噪声区域θn＝θ-θ
s-θi，其中，d0表示期望信号区域范围的一半，d
l
表示第l个干扰区域范围的一半；
15.(12)利用噪声区域内的capon功率平均值估计噪声功率：
16.噪声区域内的capon功率平均值为：
[0017][0018]
称为残留噪声功率，其中，q表示噪声区域θn中的采样点数，则噪声功率的估计值表示为：
[0019][0020]
所述步骤2的步骤包括：
[0021]
(21)根据已知的均匀线阵和步骤1中的初始波达方向角度，获取期望信号和干扰的名义导向矢量：
[0022]
l＝0,1,
…
,l-1
[0023]
(22)利用均匀线阵接收数据的采样协方差矩阵的特征向量作为与名义导向矢量垂直的误差矢量：
[0024]
基于信号子空间和噪声子空间的正交性，选出与信号源名义导向矢量最正交的特征矢量作为与名义导向矢量垂直的误差矢量，即：
[0025]
m＝1,2,
…
,m，l＝0,1,
…
,l-1
[0026]
其中，um表示按照降序排列的第m个特征值对应的特征向量，| |表示取模运算。
[0027]
(23)在步骤1中的期望信号区域和干扰区域内，基于capon功率最大化准则进行导
向矢量更新，估计得到期望信号和干扰的导向矢量：
[0028]
基于capon功率最大化，估计得到期望信号和干扰的导向矢量为：
[0029]
p＝1,2,
…
,p，l＝0,1,
…
,l-1
[0030]
其中，
[0031][0032]
表示第l个导向矢量第p次更新对应的导向矢量，η
p
表示在[-b,b]之间以δ为间隔的第p个值，b表示搜索范围的边界，p表示迭代的总次数，|| ||2表示矩阵或者向量的l2范数。
[0033]
所述步骤3中，利用估计的噪声功率以及期望信号和干扰的导向矢量重构干扰加噪声协方差矩阵为：
[0034][0035]
其中，表示估计得到的干扰功率，i表示单位对角矩阵；
[0036]
根据非圆系数的估计方式，得到校准后的期望信号和干扰的非圆系数为：
[0037]
l＝0,1,
…
,l-1
[0038]
其中，
*
表示矩阵或者向量的共轭运算，表示阵列接收数据的伪协方差矩阵，和表示扩展阵列接收数据协方差矩阵中的块矩阵，即满足：
[0039][0040]
所述步骤4中，基于估计的导向矢量，重构伪协方差矩阵，并进行期望信号导向矢量的扩展以及协方差矩阵的扩展，基于扩展的期望信号导向矢量以及协方差矩阵，对阵列接收的信号进行波束形成的步骤包括：
[0041]
根据估计得到的导向矢量以及非圆系数，则重构出干扰的伪协方差矩阵以及期望信号正交分量的协方差矩阵为：
[0042][0043][0044]
扩展的期望信号导向矢量表示为：
[0045][0046]
基于重构的干扰加噪声协方差矩阵和伪协方差矩阵，重构扩展后的干扰加噪声协方差矩阵为：
[0047][0048]
该波束形成器的权矢量表示为：
[0049][0050]
基于该权矢量，对阵列扩展的接收数据进行波束形成，得到波束形成器的输出结果为：
[0051][0052]
其中，为扩展的阵列接收数据。
[0053]
目前大部分宽线性波束形成算法对于非圆系数的估计采用构造凸优化问题的求解方法，其计算复杂度为o(m
3.5
)，其中o表示上界，而且随着阵元数目的增加，计算复杂度明显上升，不利于在实际中的实施。此外，传统方法对于协方差矩阵的重构更多的是采取积分重构的方法，然而这类方法重构的结果通常存在较多的冗余成分，即重构精度低，导致这类方法的性能提升有限。
[0054]
由上述本发明提供的技术方案可以看出，本发明通过构造与名义导向矢量垂直的误差矢量，并以最大化capon功率为目标，实现了导向矢量的估计，本发明的计算复杂度为o(pm2)，避免了传统方法通过构造凸优化问题求解计算复杂度高的问题。同时，本发明基于估计的导向矢量，进行了干扰加噪声协方差矩阵的重构、非圆系数的估计以及伪协方差矩阵的重构，不仅降低了重构的复杂度，而且还降低了重构协方差矩阵中的冗余成分，进一步提高了波束形成器的性能。
附图说明
[0055]
为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单的介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域的普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他附图。
[0056]
图1为本发明实施例提供的一种基于非高斯非圆信号特性的稳健自适应波束形成方法流程图；
[0057]
图2为本发明实施例提供的线阵信号接收模型的示意图，可以使用其他阵型；
[0058]
图3为本发明实施例提供的m＝10阵元的均匀线阵，阵元间距为半波长，信号源为二进制相移键控(binaryphase shiftkeying，bpsk)信号，期望信号来自θ0＝-5
°
，非圆相位为30
°
，干扰来自θ1＝-40
°
和θ2＝30
°
，非圆相位分别为-120
°
和60
°
，并且存在3
°
的角度估计误差。本发明方法中b＝0.1，δ＝0.01。本发明方法为proposed，对比方法分别为：理论最优
宽线性波形形成器(optimal(wl))，理论最优mvdr波束形成器，二次约束最小离差波束形成器(qcmd)，宽线性二次约束最小离差(wl-qcmd)，宽线性协方差矩阵重构(wl-incm)和基于梯度搜索的协方差矩阵重构(incm-gradient)方法，宽线性稳健capon波束形成算法1(wl-rcb1)和宽线性稳健capon波束形成算法2(wl-rcb2)。在波达方向误差服从[-4
°
,4
°
]上的均匀分布，200次蒙特卡洛实验下不同方法随信噪比(signal-to-noiseratio,snr)的性能曲线。
具体实施方式
[0059]
下面结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明的保护范围。
[0060]
本发明实施例提供一种基于非高斯非圆信号特性的稳健自适应波束形成方法，如图1所示，该方法主要包括如下步骤：
[0061]
步骤1、利用capon功率谱获取期望信号和干扰的初始波达方向角度，并将全空间划分为期望信号区域、干扰区域和噪声区域，再利用噪声区域内的capon功率平均值估计噪声功率；
[0062]
步骤2、根据已知的均匀线阵阵列结构和步骤1中的初始波达方向角度，获取期望信号和干扰的名义导向矢量；利用均匀线阵接收数据的采样协方差矩阵的特征向量作为与名义导向矢量垂直的误差矢量；在步骤1中的期望信号区域和干扰区域内，基于capon功率最大化准则进行导向矢量更新，估计得到期望信号和干扰的导向矢量；
[0063]
步骤3、利用步骤1中估计的噪声功率以及步骤2中估计的期望信号和干扰的导向矢量重构干扰加噪声协方差矩阵，并估计期望信号和干扰的非圆系数；
[0064]
步骤4、基于步骤2中估计的导向矢量以及步骤3中估计的非圆系数，重构伪协方差矩阵，并进行期望信号导向矢量的扩展以及协方差矩阵的扩展，基于扩展的期望信号导向矢量以及协方差矩阵，对阵列接收的信号进行波束形成。
[0065]
为了便于理解，首先介绍信号的接收模型以及非高斯非圆信号的特点，然后针对上述四个步骤做详细的说明。
[0066]
本发明实施例适用于任意类型的阵列形式，包括线阵、圆阵、互质阵等。为了计算方便起见，这里只针对线阵进行讨论，具体的阵列信号模型如下：
[0067]
如图2所示的m元均匀线阵为例，阵元间距为d(这里设置为信号源波长的一半)，接收l个远场窄带非高斯非圆信号源，包括一个期望信号和l-1个干扰，则阵列在时刻k的接收数据可以表示为：
[0068][0069]
其中，s0(k)表示期望信号在时刻k的波形，a0表示期望信号的导向矢量，s
l
(k)，l＝1,2,
…
,l-1表示第l个干扰在时刻k的波形，a
l
表示第l个干扰的导向矢量，xn(k)表示阵列在时刻k接收的噪声，表示阵列在时刻k接收的干扰和噪声分量。扩展
的阵列接收数据可以表示为：
[0070][0071]
其中，t表示矩阵或者向量的转置运算，h表示矩阵或者向量的共轭转置运算，
*
表示矩阵或者向量的共轭运算。表示扩展的导向矢量，0m表示m
×
1维的全零矢量。扩展的干扰加噪声分量。进一步地，扩展的阵列接收数据可以表示为：
[0072][0073]
其中，表示期望信号的扩展导向矢量，表示扩展的非期望信号分量，表示期望信号的非圆系数，e{}表示数学期望运算，φ0表示期望信号的非圆相位，| |表示取模运算。表示期望信号的功率，s0′
(k)表示期望信号的单位正交分量，即满足
[0074]
本发明分以下四个步骤实施：
[0075]
步骤1、利用capon功率谱获取期望信号和干扰的初始波达方向角度，并将全空间划分为期望信号区域、干扰区域和噪声区域，再利用噪声区域内的capon功率平均值估计噪声功率；
[0076]
步骤2、根据已知的均匀线阵阵列结构和步骤1中的初始波达方向角度，获取期望信号和干扰的名义导向矢量；利用均匀线阵接收数据的采样协方差矩阵的特征向量作为与名义导向矢量垂直的误差矢量；在步骤1中的期望信号区域和干扰区域内，基于capon功率最大化准则进行导向矢量更新，估计得到期望信号和干扰的导向矢量；
[0077]
步骤3、利用步骤1中估计的噪声功率以及步骤2中估计的期望信号和干扰的导向矢量重构干扰加噪声协方差矩阵，并估计期望信号和干扰的非圆系数；
[0078]
步骤4、基于步骤2中估计的导向矢量以及步骤3中估计的非圆系数，重构伪协方差矩阵，并进行期望信号导向矢量的扩展以及协方差矩阵的扩展，基于扩展的期望信号导向矢量以及协方差矩阵，对阵列接收的信号进行波束形成。
[0079]
所述步骤1具体包括：
[0080]
(11)利用capon功率谱获取期望信号和干扰的初始波达方向角度，并将全空间划分为期望信号区域、干扰区域和噪声区域：
[0081]
对于角度θ来说，其对应的capon功率为：
[0082]
θ∈θ
[0083]
其中，表示角度θ对应的名义导向矢量，m表示阵元数，
t
表示矩阵或者向量的转置运算。λ＝v/f为窄带信号源的波长，v表示信号源的传播速度，f表示信号源的频率。表示阵列接收数据的采样协方差矩阵，k表示快拍数，x(k)表示阵列在时刻k接收的数据，h表示矩阵或者向量的共轭转置运算，θ表示全空间，计算全空间的capon功率谱，通过谱峰搜索，获取期望信号和干扰的初始波达方向角度，记为l为期望信号和干扰的总数；
[0084]
依据估计得到的初始波达方向角度，将全空间划分为期望信号区域干扰区域θi＝θ1∪θ2∪
…
∪θ
l-1
和噪声区域θn＝θ-θ
s-θi，其中，d0表示期望信号区域范围的一半，d
l
表示第l个干扰区域范围的一半；
[0085]
(12)利用噪声区域内的capon功率平均值估计噪声功率：
[0086]
噪声区域内的capon功率平均值为：
[0087][0088]
称为残留噪声功率，其中，q表示噪声区域θn中的采样点数，则噪声功率的估计值表示为：
[0089][0090]
所述步骤2的步骤包括：
[0091]
(21)根据已知的均匀线阵和步骤1中的初始波达方向角度，获取期望信号和干扰的名义导向矢量：
[0092]
l＝0,1,
…
,l-1
[0093]
(22)利用均匀线阵接收数据的采样协方差矩阵的特征向量作为与名义导向矢量垂直的误差矢量：
[0094]
基于信号子空间和噪声子空间的正交性，选出与信号源名义导向矢量最正交的特征矢量作为与名义导向矢量垂直的误差矢量，即：
[0095]
m＝1,2,
…
,m，l＝0,1,
…
,l-1
[0096]
其中，um表示按照降序排列的第m个特征值对应的特征向量，| |表示取模运算。
[0097]
(23)在步骤1中的期望信号区域和干扰区域内，基于capon功率最大化准则进行导向矢量更新，估计得到期望信号和干扰的导向矢量：
[0098]
基于capon功率最大化，估计得到期望信号和干扰的导向矢量为：
[0099]
p＝1,2,
…
,p，l＝0,1,
…
,l-1
[0100]
其中，
[0101][0102]
表示第l个导向矢量第p次更新对应的导向矢量，η
p
表示在[-b,b]之间以δ为间隔的第p个值，b表示搜索范围的边界，p表示迭代的总次数，|| ||2表示矩阵或者向量的l2范数。
[0103]
所述步骤3中，利用估计的噪声功率以及期望信号和干扰的导向矢量重构干扰加噪声协方差矩阵为：
[0104][0105]
其中，表示估计得到的干扰功率，i表示单位对角矩阵；
[0106]
根据非圆系数的估计方式，得到校准后的期望信号和干扰的非圆系数为：
[0107]
l＝0,1,
…
,l-1
[0108]
其中，
*
表示矩阵或者向量的共轭运算，表示阵列接收数据的伪协方差矩阵，和表示扩展阵列接收数据协方差矩阵中的块矩阵，即满足：
[0109][0110]
所述步骤4中，基于估计的导向矢量，重构伪协方差矩阵，并进行期望信号导向矢量的扩展以及协方差矩阵的扩展，基于扩展的期望信号导向矢量以及协方差矩阵，对阵列接收的信号进行波束形成的步骤包括：
[0111]
根据估计得到的导向矢量以及非圆系数，则重构出干扰的伪协方差矩阵以及期望信号正交分量的协方差矩阵为：
[0112][0113][0114]
扩展的期望信号导向矢量表示为：
[0115][0116]
基于重构的干扰加噪声协方差矩阵和伪协方差矩阵，重构扩展后的干扰加噪声协方差矩阵为：
[0117][0118]
该波束形成器的权矢量表示为：
[0119][0120]
基于该权矢量，对阵列扩展的接收数据进行波束形成，得到波束形成器的输出结果为：
[0121][0122]
其中，为扩展的阵列接收数据。
[0123]
图3中给出的在干噪比20db的条件下，波达方向误差服从[-4
°
,4
°
]上的均匀分布，200次蒙特卡洛实验下不同方法随信噪比(signal-to-noise ratio,snr)的性能曲线。从图3中可以看出，本发明所提供的方法的输出信干噪比超过了optimal(mvdr)方法的输出信干噪比，并且能够达到接近optimal(wl)的输出信干噪比，体现了本发明所提供方法性能的优越性；同时也可以看出，在此误差条件下，本发明所提供方法的输出信干噪比较incm-gradient方法和wl-incm方法的输出信干噪比至少提高了3分贝，表明了本发明所提供方法的有效性；对比其他方法如wl-qcmd、qcmd、wl-rcb1和wl-rcb2等，本发明具有更显著的性能提升，表现了本发明所提供方法在此误差条件下的稳健性。此外，本发明不涉及任何凸优化问题的求解，因此避免了优化工具箱的使用，计算复杂度相对较低，更有利于在实际中的应用。
[0124]
通过以上的实施方式的描述，本领域的技术人员可以清楚地了解到上述实施例可以通过软件实现，也可以借助软件加必要的通用硬件平台的方式来实现。基于这样的理解，上述实施例的技术方案可以以软件产品的形式体现出来，该软件产品可以存储在一个非易失性存储介质(可以是cd-rom，u盘，移动硬盘等)中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述的方法。
[0125]
以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明披露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应该以权利要求书的保护范围为准。