基于波群分析的水底沉积层多层介质声学反射时域响应解析解计算方法与流程

1.本发明涉及水声技术领域，具体涉及一种基于波群分析的水底沉积层多层介质声学反射时域响应解析解计算方法。


背景技术：

2.当前由于我国对海洋资源开发的逐渐深入，海底测绘、水下通信、海洋环境监测、水下预警体系建立等领域的研究得到了国家的重视，对我国经济建设、国防实力提升有着重要意义。声波作为目前为止最适合进行水下信息传输的载体，其在水下环境中的传播机理是海洋资源开发相关研究中极为重要的研究内容。
3.目前，对于声波在海洋中远距离传播模型的研究一般都是基于稳态条件下的声波导管理论。此类模型的应用前提是当声源稳定工作一段时间后，水下声场区域稳定时，对水下声场的空间分布进行频域分析，最终总结归纳出不同频率声波的传播规律得到水下声传播的频域响应。然而在声学的实际工程应用中，使用的声波信号形式几乎都是脉冲信号。随着对海洋资源开发的深入，仅靠水下环境的声学频域响应已无法有效的指导工程实践，因此需要对水下环境的声学时域响应进行研究。其中对水底沉积层多层介质声学反射时域响应的研究是水下环境的声学时域响应研究中的一个重要的研究内容。
4.声学反射现象的原理本身并不复杂，当声波接触到不同特性阻抗介质的分界面时，受到声传播连续性的限制，会发生反射、透射现象，即入射波会在介质分界面处被分解为反射波和透射波。然而当声波在多个介质分界面中往复移动时，每碰到一次介质分界面都会产生新的反射波和透射波，新产生的声波经过二次反射、透射又会产生更多的声波，这使得多层介质的反射波组成极为复杂。
5.目前国内外关于多层介质的时域响应理论数据，大多是在声波的反射原理基础上通过模拟得到的。由于声波的数量随介质层数和反射次数成指数型增加，大部分声波的理论值只能到达三层介质的两到三次反射的水平，与声波在多层介质中反射的实际情况有着较大的差别。
6.基于此，做出本技术。


技术实现要素：

7.为了解决现有技术中存在的上述缺陷，本发明提供了一种基于波群分析的水底沉积层多层介质声学反射时域响应解析解计算方法。
8.为了实现上述目的，本发明采取的技术方案如下：
9.一种基于波群分析的水底沉积层多层介质声学反射时域响应解析解计算方法，包括如下：
10.步骤1、对水底沉积层多层介质的每一层介质按顺序依次编号；
11.步骤2、确定每一层介质的阻抗和声速；
12.步骤3、确定每一层介质的厚度；
13.步骤4、将一模拟声源放入某一层介质中，模拟声源在介质中多次反射、透射后分解为透射波群和反射波群；
14.步骤5、对每一层介质的波群进行编号；
15.步骤6、获得该模拟声源在该层介质中的反射波群表达式；
16.步骤7、根据反射波群表达式结合介质层数、模拟声源所在的介质层、以及每层介质的阻抗、声速和厚度，获得多层介质剖面声学模型；
17.步骤8、通过多层介质剖面声学模型计算每一层介质的波群时域响应；
18.步骤9、最终得到多层介质的声学反射时域响应的解析解。
19.作为优选，所述步骤1中，对每一层介质的编号遵循从小到大、从上到下的规则进行。
20.作为优选，所述步骤3中，设定最上层介质与最下层介质的厚度为正无穷。
21.作为优选，所述步骤5中，对每一层介质的波群按照方向、来源和触碰次数进行编号，与频率、时间变量无关。
22.作为优选，所述步骤5中，不同编号的波群，到达接收器的时间与波群编号的大小无关。
23.作为优选，所述步骤5中，当波群的编号趋近于无穷大时，可以将其中所有的声波幅值视为0。
24.作为优选，所述步骤7中，需要将模拟声源逐次上移至最上层介质，最终得到多层介质剖面声学模型；当模拟声源移动至其他层介质时，声波方向和编号发生变化，同时结合相应介质层的阻抗，获得该层介质下反射波群的表达式，最终获得模拟声源在该层介质中的多层介质剖面声学模型，并归一化。
25.作为优选，所述步骤8中，计算波群时域响应时，模拟声源的位置处于最下一层介质内部，而非外部。
26.与现有技术相比，本发明能实现如下有益技术效果：
27.本发明基于波群分析的水底沉积层多层介质声学反射时域响应解析解计算方法，解决了多层介质反射时域响应缺少解析解的难题，仅占用极少的计算资源就可以得到十层以上三次反射的声波时域响应，更契合声波在多层介质中反射的实际情况，同时为相关领域的研究提供更为准确的理论与数据支撑。
附图说明
28.图1为本发明多层介质时域响应的波群分析示意图；
29.图2为实施例1三层介质时域响应的波群计算的三层介质剖面声学模型示意图一(声源a在1#介质层中)；
30.图3为实施例1三层介质时域响应的波群计算的三层介质剖面声学模型示意图二(声源a在0#介质层中)；
31.图4为实施例2多层介质时域响应的波群计算的多层介质剖面声学模型示意图(声源a在n-1#介质层中)。
具体实施方式
32.为了使本发明的技术手段及其所能达到的技术效果，能够更清楚更完善的披露，兹提供了以下实施例，并结合附图作如下详细说明：
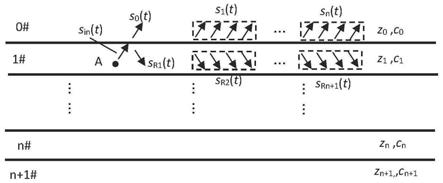
33.请参阅图1，假设一水下地层剖面结构模型共有n+2层介质，各层介质编号与相对应的特性阻抗z和声速c依次为z0、z1、zn，
……
，z
n+1
和c0、c1、cn，
……
，c
n+1
，0#介质层与n+1#介质层的厚度为正无穷。而后将一声源a放入1#介质层中，发射垂直于0#、1#介质层分界面向上的平面波s
in
(t)，声波到达0#、1#介质层分界面后会分为透射波s0(t)与反射波s
r1
(t)两部分。s
r1
(t)返回剖面结构后，经过其他介质层分界面多次的反射、透射，最终会重新回到0#、1#介质层分界面，并分成s1(t)与s
r2
(t)两个部分。为了便于论述，可以称s1(t)为一阶透射波群。而后s
r2
(t)返回剖面结构中，这样无限循环，组成了由声源a产生的地层剖面透射波形信号s(t)：
34.s(t)＝s0(t)+s1(t)+
…
+sn(t)
ꢀꢀꢀꢀꢀ
(1)
35.每一束声波在接触到0#、1#介质层分界面后都会分解成透射波与反射波，而后反射波形成新的波群。若将每一束透射波和与之对应的透射波群间的系统函数用h(t)表示，则有：
36.sn(t)＝s
n-1
(t)*h(t)
ꢀꢀꢀꢀ
(2)
37.公式(2)中，“*”为卷积运算符。
38.而后将sn(t)的傅里叶变换函数用sn(f)表示，h(t)的傅里叶变换函数由h(f)表示可以得到：
39.sn(f)＝s
n-1
(f)h(f)
ꢀꢀꢀ
(3)
40.因此公式(1)可以写作：
41.s(f)＝s0(f)+s0(f)h(f)+
…
+s0(f)hn(f)
ꢀꢀꢀ
(4)
42.在公式(4)两边同时乘以h(f)，计算(4)
×
h(f)-(4)得到：
[0043][0044]
由于时间t∈[0，+∞]，则n
→
+∞，且|h(f)|＜1(f∈[0，+∞])，所以h
n+1
(f)
→
0，则有：
[0045][0046]
如果已知每一束透射波和与之对应的透射波群间的系统函数h(t)和最初的透射波s0(t)，便可以利用公式(6)计算s(t)。
[0047]
然而在实际应用中，大部分的浅地层剖面探测设备都是在剖面介质外工作，因此需要对h(t)进行修正。
[0048]
多层剖面介质中声波的构成十分复杂，为了方便论述需使用公式(7)中的符号表示各类波群：
[0049][0050]
式中，r表示方向向上，t表示方向向下，m表示波群来源的介质层编号，n为波群触
碰来源介质层的次数，具体使用方法请参阅实施例1的图2所示。
[0051]
实施例1
[0052]
请参阅图2，图2为三层介质时域响应的波群计算的三层介质剖面声学模型示意图，且声源a在1#介质层中的情况。
[0053]
本实施例三层介质剖面声学模型，每层的编号自上而下分别为0#、1#、2#，各层介质编号与相对应的特性阻抗z和声速c依次为z0、z1、z2和co、c1、c2，0#介质层与2#介质层的厚度为正无穷，1#介质层厚度为d1。设一点声源a向上发出声波。设一点声源a向上发出声波在触碰0#、1#介质分界面后，会产生由0#介质反射方向向下的反射波和由1#介质透射方向向上的透射波此时，1#介质层的反射信号r1(t)的表达式为：
[0054][0055]
由于该模型只有三层，因此仅能产生一束声波重新回到0#、1#介质层分界面。此时与间关系如公式(9)所示：
[0056][0057]
式中x1(t)易得：
[0058][0059]
其中，α1可以根据z0、z1和z2得到：
[0060][0061]
根据公式(6)可以得到，三层介质剖面模型对应的r1(f)：
[0062][0063]
便可以求出r1(t)：
[0064]
r1(t)＝ifft[r1(f)]
ꢀꢀꢀꢀꢀꢀ
(13)
[0065]
请参阅图3，图3为实施例1三层介质时域响应的波群计算的三层介质剖面声学模型示意图二(声源a在0#介质层中)；在实际应用中，大部分的浅地层剖面探测设备都是在0#介质层工作。
[0066]
在这种情况下，除变为变为变为以外，其他波束均无变化。因此可以得到：
[0067][0068]
根据公式(14)可得：
[0069][0070]
而后根据公式(13)，得到声源在0#介质中时反射波r1的表达式：
[0071][0072]
最后可以求得，当声源在0#介质中时，以为输入值，r1′
为输出值的三层介质剖面声学模型h1(f)：
[0073][0074]
为了方便叙述将公式(17)简化为：
[0075][0076]
m(z0，z1)表示声源由1#介质层移动至0#介质层(move)的函数表达式；n(z0，z1)表示以由0#介质层中声源向1#介质层发射的声波，即为基准将r1′
归一化(normalize)的函数表达式。
[0077]
实施例2
[0078]
请参阅图4，图4为实施例2多层介质时域响应的波群计算的多层介质剖面声学模型示意图(声源a在n-1#介质层中)；在了解实施例1中三层介质剖面声学模型的搭建方法后，将进一步介绍三层以上介质剖面声学模型的搭建。先假设一水下地层剖面结构模型共有n+2层介质，各层介质编号与相对应的特性阻抗z和声速c依次为z0…zn-2
、z
n-1
、zn、z
n+1
和c0…cn-2
、c
n-1
、cn、c
n+1
，0#介质层与n+1#介质层的厚度为正无穷。现有一声源a在n-1#介质层中，向上且仅向上发出平面波声波在接触到n-1#与n-2#介质层分界面时，会产生反射波与透射波反射波接触到n#介质后，由n#介质产生的反射波群rn与间的关系可以表示为：
[0079][0080]rn
继续向上传播，接触到n-1#与n-2#介质层分界面时产生的透射波群的表达式为：
[0081][0082]
其中，x
n-1
的表达式为公式(21)：
[0083][0084]
式中，a
n-1
是声波向上传播时，n-1#介质层与n-2#介质层分界面的透射系数：
[0085][0086]
根据公式(12)便可以得到
[0087][0088]
下一步便是根据公式(18)将声源移至n-2#介质层，并归一化：
[0089][0090]
随后逐渐按照以上步骤，将声源移至0#介质层，得到多层介质剖面的声学模型。
[0091]
通过公式(8)～(24)将每一层介质的波群时域响应按照编号从大到小的顺序进行计算；最终得到多层介质的声学反射时域响应的解析解。
[0092]
以上内容是结合本发明的优选实施方式对所提供技术方案所作的进一步详细说明，不能认定本发明具体实施只局限于上述这些说明，对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。