一种基于摄影测量的大型结构位移场重构方法

1.本发明属于光测实验力学技术领域，具体涉及一种大型结构位移场重构方法。


背景技术：

2.复合材料由于其质量轻、强度高、可设计性强等特点，现以广泛应用于航空航天领域。例如在各类飞机的设计过程中，往往采用复合材料作为大型加筋壁板的设计材料，以降低其重量并提高承载能力。对于大型结构而言，获取其全场变形信息较为困难，但复合材料加筋壁板在服役过程通常往往承受弯曲、压缩等载荷作用，为确保设计的可靠性，获取大型结构在加载条件下的全场位移信息具有重要工程意义。
3.对于大型结构而言，传统位移、应变传感器虽精度高、稳定性好，但无法有效获取其全场的位移信息。目前常用的全场位移测量方法主要包括基于数字图像相关的测量方法、模态叠加法、ko位移理论、逆有限元法。数字图像相关方法需要在结构表面制作人工散斑图案，且测量精度随视场的增大而减小，因此为保证测量精度，往往视场受限。模态叠加法需要利用有限元求解结构的模态振型信息进行扩展，当边界条件难以确定时，往往无法获取满意的重构结果。ko位移理论基于经典的材料力学梁理论假设，难以获取复杂结构的全场位移信息。逆有限元法是基于最小二乘原理及有限元理论建立的一种全场重构方法，但其往往编程建模复杂，工作量大。基于摄影测量的大型结构位移场重构方法目前鲜有提出。因此为满足工程实际需求，急需提出一种简便快捷的针对大型结构的位移场重构方法，从而有效获取结构的全场位移分布情况。


技术实现要素：

4.为了克服现有技术的不足，本发明提供了一种基于摄影测量的大型结构位移场重构方法，利用有限离散点的位移信息重构结构全场位移分布情况。包括以下步骤：有限元建模并进行测点选择，获取结构在有限元坐标系下各节点及所选测点的位置信息；标识点布置，随后通过单相机多摄站摄影测量方法获取有限测点在摄影测量坐标系下加载前后的位置坐标；通过奇异值分解原理求解两坐标系间的变换矩阵；利用平移矩阵获取有限测点在有限元坐标系下的位移信息；最后利用二维切比雪夫基函数将有限测点位移信息进行拓展，从而实现大型结构的位移场重构。通过设计大型飞机壁板的位移场重构实验，证实了本发明的可行性。本发明为大型结构全场位移的获取提供了一种可行的技术手段。
5.本发明解决其技术问题所采用的技术方案包括如下步骤：
6.步骤1：测点选择及有限元建模；
7.根据待测结构的几何特征建立有限元模型，得到待测结构全场n个节点处在有限元坐标系下的位置坐标信息，记为sit_xy；在n个节点中选定测点，测点的数量记为n，测点在有限元坐标系下的位置坐标信息记为sit；
8.步骤2：在测点位置布置非编码标记点，在待测结构测点以外地方布置编码标记点；
9.步骤3：对变形前后的待测结构进行单相机多摄站摄影测量，获取变形前后测点在摄影测量坐标系下的位置坐标信息；
10.步骤4：利用奇异值分解求解摄影测量坐标系与有限元坐标系间的平移矩阵；
11.步骤5：利用步骤4得到的平移矩阵，将变形前后摄影测量坐标系下测点位置信息转化到有限元坐标系下，对变形前后有限元坐标系下测点的位置信息求差值得到测点位移un×1；
12.步骤6：利用步骤1得到的n个测点和全场n个节点在有限元坐标系下的位置坐标信息和步骤5得到的在有限元坐标系下测点位移，构造二维切比雪夫多项式矩阵，从而实现对待测结构的位移场重构。
13.进一步地，所述步骤2的具体过程为：
14.在测点位置布置非编码标记点，在待测结构测点以外地方布置编码标记点；非编码标识点为两个同心圆，小圆内部为白色，同心圆之间的部分为黑色，大圆外部为白色，每个非编码标识点的形状大小相同，用于获取测点在变形前后的位置坐标信息；编码标识点为三个同心圆，最小圆内部为白色，最小圆和中间圆之间的部分为黑色；中间圆与最大圆之间的部分均分为15个小块，对于每一个小块，编码方式为：如果小块颜色为白色则表示二进制中的1，如果小块颜色为黑色则表示二进制中的0；编码标识点为15位二进制编码，对应解码过程为：以15个小块中的任意小块为起点，按指定顺序计算连续15个小块的二进制编码，从而得到该标识点的15位二进制编码，并将其转化为十进制码数，遍历完所有小块后，其中十进制码数的最小值即为该编码标记点的编码值；
15.进一步地，所述步骤3的具体过程为：
16.对变形前后的待测结构进行单相机多摄站摄影测量，获取一系列待分析图像；经过图像特征提取、标识点定位解算求解得到被测结构测点变形前后在摄影测量坐标系下的位置坐标信息；其中变形前的位置坐标矩阵记为ph1，变形后的位置坐标矩阵记为ph2。
17.进一步地，所述步骤4的具体过程为：
18.设测点在有限元坐标系和摄影测量坐标系下的坐标分别为p
femi
＝(x
femi
,y
femi
,z
femi
)和p
phoi
＝(x
phoi
,y
phoi
,z
phoi
)；所选测点的质心坐标分别为)；所选测点的质心坐标分别为和则质心坐标通过如下表达式计算得到：
[0019][0020][0021]
求解有限元坐标系和摄影测量坐标系下测点间的协方差矩阵：
[0022][0023]
利用奇异值svd分解方法将协方差矩阵进行奇异值分析得到：
[0024]
h＝uev
t
[0025]
其中v和u为正交矩阵，e为奇异值的对角矩阵；则坐标系平移的最佳旋转矩阵则为：
[0026]
r＝vu
t
[0027]
进而利用如下表达式计算得到摄影测量坐标系与有限元坐标系间的平移矩阵t：
[0028][0029]
进一步地，所述步骤5的具体过程为：
[0030]
利用步骤4得到的平移矩阵，将变形前后摄影测量坐标系下测点位置信息转化到有限元坐标系下，将转化完成后的变形前后对应测点的位置坐标信息记为p
fem_ch1
和p
fem_ch2
，则测点在有限元坐标系下的位移矩阵为un×1＝p
fem_ch2-p
fem_ch1
。
[0031]
进一步地，所述步骤6的具体过程为：
[0032]
设切比雪夫多项式表达式为cj，其中j表示阶数；选取8阶二维切比雪夫多项式作为重构基函数，j＝0,1,2,3,4,5,7,8，x、y表示坐标，具体形式如下所示：
[0033][0034]
将步骤1得到的n个测点和全场n个节点在有限元坐标系下的位置坐标信息sit和sit_xy分别代入8阶二维切比雪夫多项式中，得到对应的基函数矩阵，记为cn×8和cn×8；
[0035]
设待测结构全场节点位移矩阵为un×1；待测结构各测点和各节点处的位移矩阵视为切比雪夫基函数的加权，因此有：
[0036]
un×1＝cn×8×
k8×1[0037]
un×1＝cn×8×
k8×1[0038]
利用最小二乘原理求解系数k8×1：
[0039]
k8×1＝(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0040]
最终，利用系数矩阵k8×1和全场节点的切比雪夫基函数矩阵cn×8即求解得到待测结构全场节点对应的位移矩阵，从而实现大型结构的位移场重构：
[0041]
un×1＝cn×8×
k8×1[0042]
＝cn×8×
(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0043]
本发明的有益效果如下：
[0044]
本发明提出了一种基于摄影测量的大型结构位移场重构方法。步骤1中的有限元建模获取了结构整体的坐标位置信息，避免了复杂繁琐的几何建模过程。步骤3通过进行单相机多摄站的摄影测量过程，其过程简单、可操作性强，可以快速获取结构在加载前后有限测点的位移信息，避免了基于激光测试方法的复杂性和低效性，为全场重构提供了初始数据。步骤4、5利用奇异值分解原理计算得到两坐标系间的最佳旋转和平移矩阵，实现了摄影测量和有限元间的相互转化。步骤6巧妙地利用测点和全节点的坐标信息构造切比雪夫基函数矩阵，实现了对有限测点位移值的有效拓展，此种基函数的选取仅需获知结构的几何信息，避免了传统模态叠加法对结构繁杂的有限元建模分析过程，在保证重构精度的基础上大大降低了工作的复杂度，提高了分析效率，最终得到了如图5所示大型结构可靠的全场位移分布情况。由图6所示的对比曲线图可以看出，结构的位移重构值与实测值差距较低，验证了本发明的可靠性，为光测实验力学领域提供了一种方便、快捷、准确的技术方案。
附图说明
[0045]
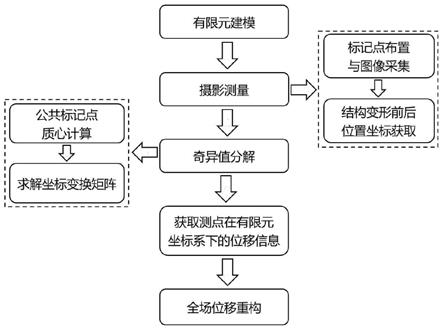
图1是本发明一种基于摄影测量的大型结构位移场重构方法流程图。
[0046]
图2是本发明实施例大型飞机壁板结构模型图。
[0047]
图3是本发明实施例大型飞机壁板测点布置示意图。
[0048]
图4是本发明实施例所用编码标记点和非编码标记点的示意图，其中(a)非编码标记点，(b)编码标记点。
[0049]
图5是本发明实施例大型飞机壁板位移场重构结果云图。
[0050]
图6是本发明实施例大型飞机壁板测点重构结果对比图。
具体实施方式
[0051]
下面结合附图和实施例对本发明进一步说明。
[0052]
为解决当前测量技术存在的问题，本发明提供了一种基于摄影测量的大型结构位移场重构方法，将摄影测量技术和切比雪夫基函数拟合理论相结合，从而有效获取了大型结构的全场位移信息。该方法具有实现简单、精度高的特点。
[0053]
本发明步骤一中的有限元建模建立了整体结构的几何特征，为重构提供了位置坐标信息。步骤二通过进行单相机多摄站的摄影测量过程，其操作简单，可以快速获取结构在加载前后测点的位置信息，为全场重构提供了可靠的初始数据。步骤三、四中利用奇异值分解原理计算得到坐标系间最佳旋转、平移矩阵，从而实现了摄影测量坐标系与有限元坐标系间的相互转换。步骤五利用测点和全节点的坐标位置信息构建二维切比雪夫基函数，实现了对有限测点位移值的有效拓展，最终得到了大型结构的全场位移分布情况。
[0054]
如图1所示，一种基于摄影测量的大型结构位移场重构方法，包括如下步骤：
[0055]
步骤1：测点选择及有限元建模；
[0056]
根据待测结构的几何特征建立有限元模型，得到待测结构全场n个节点处在有限元坐标系下的位置坐标信息，记为sit_xy；在n个节点中选定测点，测点的数量记为n，测点在有限元坐标系下的位置坐标信息记为sit；
[0057]
步骤2：在测点位置布置非编码标记点，在待测结构测点以外地方布置编码标记点；
[0058]
步骤3：对变形前后的待测结构进行单相机多摄站摄影测量，获取变形前后测点在摄影测量坐标系下的位置坐标信息；
[0059]
步骤4：利用奇异值分解求解摄影测量坐标系与有限元坐标系间的平移矩阵；
[0060]
步骤5：利用步骤4得到的平移矩阵，将变形前后摄影测量坐标系下测点位置信息转化到有限元坐标系下，对变形前后有限元坐标系下测点的位置信息求差值得到测点位移un×1；
[0061]
步骤6：利用步骤1得到的n个测点和全场n个节点在有限元坐标系下的位置坐标信息和步骤5得到的在有限元坐标系下测点位移，构造二维切比雪夫多项式矩阵，从而实现对待测结构的位移场重构。
[0062]
进一步地，所述步骤2的具体过程为：
[0063]
在测点位置布置非编码标记点，在待测结构测点以外地方布置编码标记点；非编码标识点为两个同心圆，小圆内部为白色，同心圆之间的部分为黑色，大圆外部为白色，每
个非编码标识点的形状大小相同，用于获取测点在变形前后的位置坐标信息；编码标识点为三个同心圆，最小圆内部为白色，最小圆和中间圆之间的部分为黑色；中间圆与最大圆之间的部分均分为15个小块，对于每一个小块，编码方式为：如果小块颜色为白色则表示二进制中的1，如果小块颜色为黑色则表示二进制中的0；编码标识点为15位二进制编码，对应解码过程为：对应解码过程为：以15个小块中的任意小块为起点，按指定顺序计算连续15个小块的二进制编码，从而得到该标识点的15位二进制编码，并将其转化为十进制码数，遍历完所有小块后，其中十进制码数的最小值即为该编码标记点的编码值。
[0064]
进一步地，所述步骤3的具体过程为：
[0065]
对变形前后的待测结构进行单相机多摄站摄影测量，获取一系列待分析图像；经过图像特征提取、标识点定位解算求解得到被测结构测点变形前后在摄影测量坐标系下的位置坐标信息；其中变形前的位置坐标矩阵记为ph1，变形后的位置坐标矩阵记为ph2。
[0066]
进一步地，所述步骤4的具体过程为：
[0067]
设测点在有限元坐标系和摄影测量坐标系下的坐标分别为p
femi
＝(x
femi
,y
femi
,z
femi
)和p
phoi
＝(x
phoi
,y
phoi
,z
phoi
)；质心坐标分别为)；质心坐标分别为和则质心坐标通过如下表达式计算得到：
[0068][0069][0070]
求解有限元坐标系和摄影测量坐标系下测点间的协方差矩阵：
[0071][0072]
由于最佳旋转矩阵要求两对应点间的均方根偏差取得最小值，利用奇异值(svd)分解方法将协方差矩阵进行奇异值分析得到：
[0073]
h＝uev
t
[0074]
其中v和u为正交矩阵，e为奇异值的对角矩阵；则坐标系平移的最佳旋转矩阵则为：
[0075]
r＝vu
t
[0076]
进而利用如下表达式计算得到摄影测量坐标系与有限元坐标系间的平移矩阵t：
[0077][0078]
进一步地，所述步骤5的具体过程为：
[0079]
利用步骤4得到的平移矩阵，将变形前后摄影测量坐标系下测点位置信息转化到有限元坐标系下，将转化完成后的变形前后对应测点的位置坐标信息记为p
fem_ch1
和p
fem_ch2
，则测点在有限元坐标系下的位移信息为un×1＝p
fem_ch2-p
fem_ch1
。
[0080]
进一步地，所述步骤6的具体过程为：
[0081]
设切比雪夫多项式表达式为cj，其中j表示阶数；选取8阶二维切比雪夫多项式作为重构基函数，j＝0,1,2,3,4,5,7,8，具体形式如下所示：
[0082][0083]
将步骤1得到的n个测点和全场n个节点在有限元坐标系下的位置坐标信息代入8阶二维切比雪夫多项式中，得到对应的基函数矩阵，记为cn×8和cn×8；
[0084]
设待测结构全场节点位移矩阵为un×1；待测结构各测点和各节点处的位移矩阵视为切比雪夫基函数的加权，因此有：
[0085]
un×1＝cn×8×
k8×1[0086]
un×1＝cn×8×
k8×1[0087]
利用最小二乘原理求解系数k8×1：
[0088]
k8×1＝(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0089]
最终，利用系数矩阵k8×1和全场节点的切比雪夫基函数矩阵cn×8即求解得到待测结构全场节点对应的位移矩阵，从而实现大型结构的位移场重构：
[0090]
un×1＝cn×8×
k8×1[0091]
＝cn×8×
(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0092]
具体实施例：
[0093]
1、测点选择及有限元建模。根据图2所示大型飞机壁板的几何特征建立结构的cad模型，进而进行结构的有限元建模过程，进行网格划分，得到待测结构全场n个节点处在有限元坐标系下的位置坐标信息，记为sit_xy。同时选定测点位置和测点个数如图3所示，测点位置应反应结构的变形趋势，针对此大型飞机壁板结构，测点个数选为130个、测点位置坐标信息矩阵记为sit。
[0094]
2、进行单相机多摄站摄影测量。首先根据步骤一中所确定的130个测点位置布置非编码标识点，非编码标识点表现为白色中心的同心圆形，每个点的形状大小相同，用于获取测点在变形前后的位置坐标信息。同时布置一定数量的编码标识点，为后续的摄影测量做准备。编码点中心为圆形，中心的环形为编码位，这里使用的编码标识点为15位的二进制编码标识点，白色背景对应二进制中的1，黑色背景对应二进制中的0。解算过程为：以其中一个为起始点按顺序进行解码，解出的最小编码值即为该编码标记点的编码值。这些编码标记点用于对不同位置处的相机进行解码定位，从而求解相机的位置。编码点和非编码点如图4所示。
[0095]
利用单反相机在不同位置和方向对被测大型结构的同一区域进行图像采集，进行单相机多摄站摄影测量过程，获取系列待分析图像。进而经过图像特征提取、标识点定位解算等方法求解得到被测结构有限测点在摄影测量坐标系下的位置坐标信息。其中测点在加载前的位置坐标矩阵记为ph1；加载变形后的位置坐标矩阵记为ph2。
[0096]
3、奇异值分解求解平移矩阵。利用第1步和第2步获取到的测点在两坐标系下的位置信息，通过奇异值分解方法得到坐标系转换矩阵。
[0097]
首先进行公共标记点，即所选测点的质心计算。设每个测点在有限元坐标系和摄影测量坐标系下的坐标分别为p
femi
＝(x
femi
,y
femi
,z
femi
)和p
phoi
＝(x
phoi
,y
phoi
,z
phoi
)；质心坐
标分别为和和则质心坐标可通过如下表达式计算得到：
[0098][0099][0100]
求解两坐标系下公共标记点间的协方差矩阵：
[0101][0102]
由于最佳旋转矩阵要求两对应点间的均方根偏差取得最小值，因此利用奇异值(svd)分解方法将协方差矩阵进行奇异值分析得到：
[0103]
h＝uev
t
[0104]
其中v和u为正交矩阵，e为奇异值的对角矩阵。则坐标变换的最佳旋转矩阵则为
[0105]
r＝vu
t
[0106]
进而即可利用如下表达式计算得到平移矩阵：
[0107][0108]
综上所述即求解完成了摄影测量坐标系与有限元坐标系间的变换矩阵。
[0109]
4、获取有限元坐标系下测点位移信息
[0110]
利用第3步中求解得到的矩阵r和t即可将摄影测量坐标系下加载前后测点的位置坐标信息转化到有限元坐标系下。将转化完成后的变形前后对应测点的位置坐标信息记为p
fem_ch1
和p
fem_ch2
。因此测点在有限元坐标系下的位移信息即为un×1＝p
fem_ch2-p
fem_ch1
。
[0111]
5、进行结构的位移场重构
[0112]
利用第1步得到的有限元坐标系下130个测点的位置坐标信息sit和全场节点的位置坐标信息sit_xy构造二维切比雪夫基函数矩阵，从而实现对结构整体的位移场重构。
[0113]
设切比雪夫多项式表达式为cj，其中j表示阶数。选取8阶二维切比雪夫多项式作为重构基函数，分别为0、1、2、3、4、5、7、8阶，具体形式如下所示：
[0114][0115]
将位置坐标信息sit和sit_xy分别代入上述切比雪夫基函数中，得到对应的基函数矩阵，记为cn×8和cn×8。
[0116]
设测点位移矩阵和结构全节点位移矩阵分别un×1和un×1；结构各节点处的位移信息可视为切比雪夫基函数的线性加权，因此有：
[0117]
un×1＝cn×8×
k8×1[0118]
un×1＝cn×8×
k8×1[0119]
有限测点的位移信息un×1通过摄影测量和坐标系平移过程求解得到，测点对应的切比雪夫多项式矩阵cn×8通过几何信息确定的位置坐标代入得到，因此只需要求测点数大
于基函数阶数即可利用最小二乘原理求解系数k8×1：
[0120]
k8×1＝(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0121]
最终，利用系数矩阵k8×1和全场节点的切比雪夫基函数矩阵cn×8即可求解得到结构全场节点对应的位移信息，从而实现大型结构的位移场重构。
[0122]
un×1＝cn×8×
k8×1[0123]
＝cn×8×
(cn×
8t
×cn
×8)-1
×cn
×
8t
×
un×1[0124]
图5为利用此种方法对大型飞机壁板的位移场进行重构得到的全场位移云图。
[0125]
为验证此发明的有效性，设计了大型飞机壁板的位移场重构实验，利用摄影测量获取到的130个有限测点的位移信息，通过本发明所提方法成功重构出飞机壁板的全场位移分布情况，得到了全场位移分布云图。
[0126]
图6为飞机壁板重构实验中测点的实测值与重构值的数值对比图。
[0127]
可以看出，利用本发明所提方法进行飞机壁板重构实验的重构结果与摄影测量的实测结果基本一致，可以证明所提方法的可靠性与准确性。
[0128]
综上所述，本发明公开了一种基于摄影测量的大型结构位移场重构方法，将摄影测量获取的大型结构有限测点的位移值利用二维切比雪夫基函数进行扩展，成功得到了结构全场位移分布情况，可广泛应用于大型结构的全场变形测试中。