一种不确定性条件下DNAPL污染场地修复的多目标优化方法

一种不确定性条件下dnapl污染场地修复的多目标优化方法
技术领域
1.本发明属于污染水文地质与深度学习的交叉领域，具体涉及一种不确定性条件下dnapl污染场地修复的多目标优化方法。


背景技术：

2.重非水相液体(dense non-aqueous phase liquids，dnapls)污染因其高密度、低界面张力和低粘度的特性而难以清除。较为有效的修复方法是表面活性剂加强的含水层修复，其通过注入井注入表面活性剂，抽出井抽提的方式开展地下水修复。为了同时达成地下水修复的经济效益和环境效益，常采用多目标优化来获得最优修复方案。最优方案是否切实可行取决于优化中调用的数值模型是否精确反映了实际场地特征，主要是含水层渗透率和dnapl污染源区的特征。然而，地下介质往往具有强非均质性，稀疏的观测钻孔往往不足以精确刻画出实际场地含水层渗透率以及dnapl污染源区的特性。因此，对地下水污染场地的修复方案优化需要在考虑刻画的地下介质场及污染源区具有不确定性的前提下开展。这类问题通常通过考虑地下介质场及污染源区的多个可能实现，来评估不确定性对优化结果的影响。
3.优化中考虑不确定性，会增加优化算法反复调用的模拟模型的次数，即随着所考虑的地下介质场及污染源区的实现数递增，这可能带来难以负担的计算量。为了减轻计算负担，常采用替代模型替代原本耗时的数值模型。然而，在含水层介质场及dnapl污染源区刻画不确定的条件下，替代优化算法调用sear修复dnapl数值模型面临两大挑战。
4.第一，含水层非均质性和dnapl污染源区的不确定性空间参数会导致“维数灾难(curse of dimensionality)”问题，即建立替代模型所需的计算量随着不确定参数维度的增加而呈指数型急剧增长。以往的地下水修复优化研究，常采用均化或分区策略，利用一个或几个参数概化非均质场，以此降低输入参数的维度。然而，考虑到多相流对渗透率变化非常敏感，数值模型中简化渗透率的非均质性无法反映实际场地的地下水及dnapl的运移，进而可能误导表面活性剂强化的含水层修复(surfactant enhanced aquifer remediation,sear)方案的设计。因此，需要创新的替代模型，以应对不确定条件下，sear修复dnapl多相流过程中存在的高维输入(刻画非均质渗透率场和dnapl饱和度场的高维空间参数)的挑战。第二，sear修复dnapl后得到的修复后napl相的饱和度为不连续的空间变量，现有替代模型难以较为准确的进行预测。以往常简化为一个或多个局部变量。然而，修复后的napl可能局部残留，成为一个长期污染源，对地下水质量构成威胁，仅通过整体平均的指标无法反映修复后dnapl的残留分布。因此，需要创新的替代模型，以应对替代修复后空间不连续分布的napl饱和度的挑战。
5.为解决不确定条件下优化带来的两个挑战，我们建立了深度卷积神经网络(cnn)作为替代模型，实现对刻画不确定的污染场地下采用不同修复方案产生的高维不确定输入(即非均质渗透率分布、dnapl源区结构和sear修复方案)与修复后dnapl饱和度场之间潜在关系的替代。然后建立不确定条件下的优化问题，通过优化算法非支配排序遗传算法
(nsgaii)调用替代模型cnn，形成不确定条件下的基于深度学习替代模型的多目标优化方法cnn-nsgaii，以实现在刻画具有不确定性的污染场地中高效搜索到可靠的最佳修复方案的目的。该不确定性条件下的基于深度学习的多目标优化方法的可行性通过一个三维理想算例进行了分析验证。
6.已有的替代dnapl污染源区的sear修复过程的替代模型有人工神经网络(artificial neural network)、分布聚类分析(stepwise cluster analysis)、多项式响应面(polynomial response surface)、混沌多项式展开(polynomial chaos expansion)、径向基函数(radial basis function)、克里格(kriging)、支持向量回归(support vector regression)和高斯过程(gaussian process)等。
7.地下水修复优化中采用的替代模型：1.存在维数灾难，无法实现考虑污染场地刻画存在不确定性时，非均质含水层中sear修复过程的替代；2.无法替代出修复后全局变量dnapl饱和度的空间分布，导致无法全面评价修复效果。


技术实现要素：

8.发明目的：为了克服现有技术中的不足，本发明提出一种不确定性条件下dnapl污染场地修复的多目标优化方法，实现未精细刻画的污染场地中sear修复dnapl的最优修复方案的高效获取。
9.技术方案：本发明所述的一种不确定性条件下dnapl污染场地修复的多目标优化方法，具体包括以下步骤：
10.(1)建立不确定条件下的多目标优化模型：以设置决策变量为sear治理井的流量；优化目标为最小化sear修复总费用f1和最小化修复后napl相的分布范围约束条件为治理井的流量限制；不确定条件为满足稀疏观测数据的地下介质和污染源区分布的多个实现；
11.(2)构建深度卷积神经网络模型，替代耗时的多相流数值模型，实现对sear修复dnapl的数值模型的高维替代；
12.(3)采用优化算法调用训练好的替代模型对不确定条件下的优化模型进行求解，获得不确定条件下最优的修复方案。
13.进一步地，所述步骤(1)通过以下公式实现：
[0014][0015]
其中，c1(m+n)代表m口注入井和n口抽出井的安装费用(元)；c2代表抽出井的运行费用(元/m3)；t代表修复时间；代表第j口抽出井的流量；c3代表注入井的运行费用(元/m3)；代表第i口注入井的流量；
[0016][0017]
其中，和分别代表nr个实现计算得到的修复后napl相的分布范围f2的均值和方差；λ代表风险厌恶系数，λ取2意味着置信区间为97.5％，即有97.5％的
代表第i个网格的残留的dnapl饱和度；m(
·
)是指示函数，用于指示一个网格是否有napl相；n是网格总数；
[0018]
约束条件：
[0019]
其中，q
max
和q
min
是饱和度的阈值，分别是注入井(in)和抽出井(ex)允许的最大和最小值。
[0020]
进一步地，所述步骤(2)实现过程如下：
[0021]
将数值模型的输入场和输出场转为三维图片，利用卷积操作充分提取图片数据的局部空间相关性、进而学习输入－输出图片间的潜在映射关系；其中sear修复井流量组合转化为图片的方式如下：
[0022][0023]
其中，ω＝1,
…
,w；h＝1,
…
,h；d＝1,
…
,d；j＝1,
…
n，n代表井数；s
rj
》0代表注入井；s
rj
《0代表抽出井。即，在井位置处的像素值为抽出/注入率，其他没有井的位置处的像素值为0；
[0024]
使用一个卷积层从输入图像中提取特征面，然后将提取的特征面通过多重残差密集块和下采样层交替加工，每经过一个下采样层，特征面尺寸将减半，最后输出一系列包含高层特征的特征面，这些特征面随后经过rrdb和上采样层交替加工，每经过一个上采样层，特征面尺寸将加倍，最终经过一个卷积层和激活函数sigmoid激活重构输出图像。
[0025]
进一步地，所述步骤(3)实现过程如下：
[0026]
优化算法不断搜索新的决策变量组合，通过调用训练好的替代模型在生成的地下介质和污染源区的实现集合中对决策变量组合进行评价，最终获得不确定条件下最优的修复方案。
[0027]
进一步地，所述数值模型的输入场为非均质渗透系数场、dnapl饱和度场、sear修复井流量的组合，输出场为修复后的dnapl饱和度场。
[0028]
有益效果：与现有技术相比，本发明的有益效果：本发明提出了不确定条件下，耦合深度卷积神经网络cnn和多目标优化算法nsga-ii的多目标优化方法；在考虑对于实际污染场地的非均质地下含水层和dnapl污染源区的刻画具有不确定性的情况下，实现污染场地中sear修复dnapl的最优修复方案的高效获取；本发明采取cnn替代数值模型，克服“维度诅咒”，实现在高维输入下对全局输出变量的高效预测，同时极大的减轻了不确定条件下优化问题的计算负担。
附图说明
[0029]
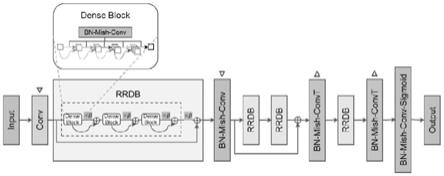
图1是深度卷积网络结构示意图；
[0030]
图2是研究区的水文地质概念模型示意图；
[0031]
图3是为渗透率(ln k)参考场和dnapl饱和度(s
n0
)参考场及ln k场和s
n0
场随机选
择的两个实现示意图；
[0032]
图4是cnn在训练和测试数据集进行评估得到的ssim大小示意图；
[0033]
图5是三种随机实现中，数值模型utchem(sn)和替代模型预测的sear修复后剩余dnapl饱和度分布的对比图；
[0034]
图6是cnn替代模拟-优化方法获得的帕累托最优解和所有实现上的(f1，f2)解图；
[0035]
图7是替代模型cnn和数值模型utchem预测的目标值dnapl分布面积f2的对比图。
具体实施方式
[0036]
下面结合附图对本发明作进一步详细说明。
[0037]
本发明提出一种不确定性条件下dnapl污染场地修复的多目标优化方法，首先，建立不确定条件下的多目标优化模型；其次，训练替代模型，实现对sear修复dnapl的数值模型的替代；最后，通过多目标优化算法直接调用替代模型实现替代模拟-优化框架。具体包括以下步骤：
[0038]
针对sear修复dnapl的优化问题，设置决策变量为sear治理井(注入井和抽提井)的流量；优化目标为1)最小化sear修复总费用f1(治理井的布置费用和运行费用)和2)最小化修复后napl相的分布范围约束条件为治理井的流量限制。考虑刻画污染场地具有不确定性，满足稀疏观测数据的地下介质和污染源区具有很多实现，因此在这种不确定条件下进行优化，采用类似不确定性分析的策略，综合考虑所有实现，定义不确定条件下的优化目标建立的不确定条件下的多目标优化模型如下：
[0039]
目标函数1：其中，c1(m+n)代表m口注入井和n口抽出井的安装费用(元)；c2代表抽出井的运行费用(元/m3)；t代表修复时间；代表第j口抽出井的流量；c3代表注入井的运行费用(元/m3)；代表第i口注入井的流量。
[0040]
目标函数2：其中，和分别代表nr个实现计算得到的f2的均值和方差；λ代表风险厌恶系数，λ取2意味着置信区间为97.5％，即有97.5％的代表第i个网格的残留的dnapl饱和度；m(
·
)是指示函数，用于指示一个网格是否有napl相；n是网格总数。
[0041]
约束条件：其中，q
max
和q
min
是饱和度的阈值，分别是注入井(in)和抽出井(ex)允许的最大和最小值。
[0042]
使用常见的非支配排序遗传算法(non-dominated sorting genetic algorithm-ii，nsga-ii)(deb等，2002)解决上述双目标优化问题。nsga-ii算法提供一组称为帕累托最
优集的解，它代表冲突目标之间的权衡解。
[0043]
为了实现替代优化模型中调用的sear修复dnapl的多相流数值模型，首先需要运行多相流数值模型生成训练样本，训练样本的输入变量为非均质渗透系数场、dnapl饱和度场和sear修复井流量组合，输出变量为修复后的dnapl饱和度场。然后利用训练样本对替代模型进行训练。
[0044]
采用优化算法调用训练好的替代模型对不确定条件下的优化模型进行求解。具体为，优化算法不断搜索新的决策变量组合，通过调用训练好的替代模型在生成的地下介质和污染源区的实现集合中对决策变量组合进行评价，最终获得不确定条件下最优的修复方案。
[0045]
使用德克萨斯大学化学成分模拟器(utchem)来模拟sear治理dnapl污染源区的多相流运移过程，用于生成替代模型的训练样本。utchem是一个三维多相流模拟器，可以模拟多组分污染物运移、复杂的地球化学反应和有机物溶解。
[0046]
深度卷积神经网络cnn作为深度神经网络的一种，适用于对图像数据的处理。因而，在替代sear修复dnapl过程中的多相流数值模型时，需要将数值模型的输入场(非均质渗透系数场、dnapl饱和度场、sear修复井流量组合)和输出场(修复后的dnapl饱和度场)转为三维图片(即像素矩阵，大小为d
×h×
w)，利用卷积操作充分提取图片数据的局部空间相关性、进而学习输入－输出图片间的潜在映射关系。其中sear修复井流量组合转化为图片的方式如下：
[0047][0048]
其中，ω＝1,
…
,w；h＝1,
…
,h；d＝1,
…
,d；j＝1,
…
n，n代表井数；s
rj
》0代表注入井；s
rj
《0代表抽出井。即，在井位置处的像素值为抽出/注入率，其他没有井的位置处的像素值为0。
[0049]
深度卷积神经网络cnn对高维输入图片进行粗化到精炼(coarsen-to-refine)加工。在这个过程中，网络内提取的特征面尺寸经过了一个先变小然后再恢复的过程，以充分提取数据中隐含的多尺度和分层特征，进而高效学习系统的输入－输出映射关系。实现这一过程的基本网络架构如图1所示。首先使用一个卷积层(conv)(goodfellow，2016)从输入图像中提取特征面，然后将提取的特征面通过多重残差密集块(residual-in-residual dense block，rrdb)(wang等，2018)和下采样层(
▽
)交替加工，每经过一个下采样层，特征面尺寸将减半，最后输出一系列包含高层特征的特征面，这些特征面随后经过rrdb和上采样层(δ)交替加工，每经过一个上采样层，特征面尺寸将加倍，最终经过一个卷积层和激活函数sigmoid激活重构输出图像。网络的中间部分采用2个连续的rrdb，并应用了一个额外的残差学习(输出和输入相加)，以促进这部分(特征面尺寸最小时)信息流的传导。
[0050]
生成满足观测数据的地下介质渗透率k场和污染源区napl相饱和度s
n0
场的实现集合，分别用于生成训练样本和求解优化模型。绝对渗透率k场采用地质统计软件库(gslib)中的有条件的序贯高斯模拟(conditional sgsim)，取用钻孔获得的先验k值作为条件输入，生成符合先验信息的渗透率实现。在渗透率实现对应的含水层中，利用随机侵入渗流(stochastic invasion percolation，sip)算法模拟dnapl泄漏，获得稳态的初始napl相饱
和度(s
n0
)分布。接着根据钻孔获得的先验s
n0
值，利用拒绝采样(rejection sampling，rs)算法，从初始dnapl饱和度实现中筛选出符合先验信息的dnapl饱和度实现。
[0051]
通过数值实验说明了深度卷积神经网络替代模拟-优化方法的可行性。算例是一个3维非均质承压含水层45m
×
25m
×
10m；如图2所示，圆柱体代表假想钻孔，获得渗透率和dnapl饱和度观测值；带有上/下箭头的钻孔分别为抽/注水井；灰度图和等值体分别代表渗透率和napl相的分布。含水层均匀离散成45
×
25
×
10＝11250个单元格。含水层左右边界设置为定水头边界，水力梯度为0.001，其余边界均为零通量边界。参数设定详见表1。
[0052]
表1数值实验中的参数设置
[0053]
[0054][0055]
渗透率k场实现由地质统计软件库(gslib)中的有条件的序贯高斯模拟(conditional sgsim)生成，参数详见表1，假定采样得到共计150个先验k值作为条件输入。在每个渗透率实现对应的含水层中，以点源形式在含水层顶部中心渗漏三氯乙烯(tce)，采用随机侵入渗流(stochastic invasion percolation，sip)算法生成初始dnapl饱和度(s
n0
)的实现，接着基于假定采样得到的共计150个先验s
n0
值，采用拒绝采样算法筛选出符合先验信息的dnapl饱和度实现，如图3所示，图3是第一列为渗透率(ln k)参考场和dnapl饱和度(s
n0
)参考场，右两列展示的是ln k场和s
n0
场随机选择的两个实现，两个场均根据15个观测井(垂直圆柱体)获得的渗透率和饱和度观测值作为先验信息生成。
[0056]
sear修复共设置m＝6个注入井和n＝3个抽出井，如图2所示，修复时间设置为30天，井的安装费用系数c1设置为5000元，抽出井的运行费用系数c2设置为0.5元/m3，注入井的运行费用系数c3设置为201.5元/m3，注入井和抽出井的流量范围分别设置为和和通过收敛性分析确定用于不确定优化的实现的个数nr为500。
[0057]
替代模型需要替代的是优化问题中的目标函数f2，即从输入变量(渗透率k场、dnapl饱和度场s
n0
、sear井流量s)到输出变量(修复后dnapl饱和度场sn)的替代。我们选择生成5000个训练样本对cnn进行训练。网络训练的主要超参数设置为：初始学习率(learning rate)为0.005、批大小(batch size)为24。在nvidiatesla v100 gpu训练200个epoch获得训练后模型。训练精度采用结构相似性指标(structural similarity index，ssim)(wang等，2004)刻画。ssim是量化两个2-d图片之间结构相似性的指标，计算大小为d
×h×
w的3-d图片的ssim时，需要将三维图片转化为d张h
×
w的2-d图片。ssim越接近1.0说明训练效果越好。
[0058]
优化算法nsga-ii调用训练后的cnn模型对优化模型进行求解。优化算法的主要参数设置为：种群数为100，优化代数为100，变异概率为0.11，交叉概率为0.70。
[0059]
图4显示了cnn替代三维多相流运移模型的替代精度。可以看出，cnn替代模型在5000个训练样本上替代精度指标ssim的中值为0.995，在1000个测试样本上得到的ssim的中值为0.991，这表明cnn能够较精确的预测sear修复后dnapl饱和度的空间分布。
[0060]
图5进一步说明了cnn可以较为准确的预测修复后的dnapl饱和度sn场。图中比较了测试集中三个随机实现上utchem模拟的sn场、cnn预测的场和两者之间的差异。可以看出，尽管饱和度场在空间上复杂且不连续，但cnn的预测与utchem的非常接近，且在大多数区域的预测误差都小于0.05。因此，在接下来求解优化模型时，使用优化算法直接调用这种预测较为准确但速度更快的替代模型cnn，替代耗时的多相流数值模型。
[0061]
分析优化到最后一代获得的最优修复方案。图6是cnn替代模拟-优化方法获得的帕累托最优解(圆圈)和所有实现上的(f1，f2)解(方块)，显示了在考虑500个实现时获得的的最优帕累托前沿和求解目标函数时计算的500个实现的目标函数f2值。可以看出，帕累托前沿是非线性的，并且呈现出修复成本越高，修复后napl越少的趋势，
这与实际情况相符。因此，不确定性优化方法可以获取正确趋势的帕累托最优解。
[0062]
为了说明基于cnn的优化算法获得的帕累托解是可靠的，将cnn替代模型预测的目标函数f2值与utchem的模拟结果进行了比较。如图7所示，cnn与utchem得到的f2值的散点基本分布在1:1对角线上，这意味着替代模型cnn的预测值与utchem数值模型的模拟结果非常一致；两者的绝对误差主要在(-40m2，20m2)之间，相对于网格总面积(11250m2)非常小。因此，优化算法nsga-ii通过调用替代模型cnn可以获得可靠的帕累托最优前沿。
[0063]
使用替代模型来解决优化问题的根本目的是减轻计算负担，如表2所示。
[0064]
表2计算效率对比
[0065][0066]
在这种不确定条件下的优化问题中，不采用替代模型(utchem-nsgaii)，需要至少4000000次数值模拟才能达到收敛并获得最优解，即考虑500个实现时，100个种群，并在nsga-ii算法中迭代至少80代。单次模拟平均耗时约12分钟，总运行时间约为800000小时。采用替代模型(cnn-nsgaii)，替代优化过程中调用的4000000个数值模型仅需约129.5小时即可。此前，需要1240小时进行6000次数值模拟，生成6000个训练样本，并且需要5.5小时用于训练替代模型。总的来说，cnn-nsgaii的成本仅为1375小时，比utchem-nsgaii的800000小时的成本节省了99.8％的时间。