一种基于等效偶极矩和物理光学法的高效电磁散射方法

1.本发明属于电磁场建模仿真技术领域，具体涉及一种基于等效偶极矩和物理光学法的高效电磁散射方法。


背景技术：

2.电磁场数值计算方法已经发展的相当成熟，然而，计算精度和效率之间的权衡仍然没有得到很好的解决。电磁场数值方法可分为低频方法和高频方法，低频方法如：矩量法(method ofmoment，mom)和有限元法(finite element method，fem)等，在处理包含精细结构的目标体时，可以保证相当高的精度；高频方法如：物理光学法(physical optics，po)和几何光学法(geometric optics，go)等，以牺牲计算精度为代价，可以极大提高计算效率。
3.随着目标电尺寸的增大和计算频点的增多，现有的数值方法所需的计算时间非常长，不能满足实际工程领域许多电磁问题高效分析的要求。因此需要提出新的改进方法，目前对电磁数值计算方法的改进主要体现在两个方面：一是改进算法本身，采用高低频混合方法，如：mom-po等；二是针对计算过程进行改进，如等效偶极矩法(equivalent dipole moment，edm)和快速多极子方法(fast multipole method，fmm)等。
4.文献“an efficient hybrid method of iterative mom-po and equivalent dipole-moment for scattering from electrically large objects”公开了一种将等效偶极矩方法应用于迭代形式的mom-po中的方法，分析了pec复合物体的电磁散射特性；文献“efficient electromagnetic analysis for complex planar thin-layer composite objects by a hybrid method”公开了一种利用等效偶极矩方法加速贴片天线阵列电磁特性分析的方法。但目前所提出的等效偶极矩方法只分析了pec物体的散射，对于各向同性和各向异性物体特性的分析，现有算法如mom-po也可以处理，但效率不高，尤其是电大尺寸目标，计算时间往往难以接受。


技术实现要素：

5.本发明的目的是克服上述现有技术的缺陷，提供一种基于等效偶极矩和物理光学法的高效电磁散射方法，全面分析了pec、各向同性和各向异性介质涂敷pec物体的电磁散射特性，并且利用edm方法大大减少cpu计算时间，利用高阶阻抗边界条件保证了较好的精度，并减少了计算机内存占用。
6.本发明所提出的技术问题是这样解决的：
7.一种基于等效偶极矩和物理光学法的高效电磁散射方法，利用电磁仿真软件将目标表面以三角形网格划分，根据目标表面曲率半径将目标表面划分为mom区域和po区域，该方法计算过程分为三个部分，第一部分用于处理mom区域，第二部分用于计算po区域的电磁流，第三部分用于计算mom区域和po区域的耦合作用。
8.本发明所述方法具体包括以下步骤：
9.步骤1.在电磁仿真软件中建立散射体模型，设置电磁波频率和三角形边长，利用
电磁仿真软件对模型表面进行三角形网格划分，导出每个三角形序号和顶点坐标；
10.步骤2.记录每个三角形的中心坐标及面积，将相邻三角形组成一个三角面元对，编号并记录三角对的个数n，记录每对三角面元对的公共边长度；
11.步骤3.对模型进行分区，将曲率半径大于10个波长的区域划分为物理光学区即po区，将其他区域划分为矩量区即mom区；
12.步骤4.mom区的处理采用矩量法计算；
13.步骤4-0.将散射体模型的表面等效电流和等效磁流用rwg基函数离散：
[0014][0015][0016][0017]
其中，j(r')为等效电流，m(r')为等效磁流，r'为散射体模型的表面任意点，1≤n≤n，n为基函数个数，fn(r')为第n个rwg基函数，an和bn分别为等效电流和等效磁流中第n个rwg基函数的展开系数；表示第n个三角面元对的正负三角形，表示第n个三角面元对正负三角形的面积，ln表示第n个三角面元对的公共边长度，表示自由顶点和正负三角形中心所连成的向量；
[0018]
步骤4-1.在mom区域构建散射体模型表面的电场积分方程，并将用rwg基函数展开后的等效电流和等效磁流代入电场积分方程，得到离散后的电场积分方程；
[0019]
步骤4-2.对离散后的电场积分方程等式两端采用伽辽金检验，即对方程两端同时用n个rwg基函数作内积，将方程个数扩展为n个，得到电场积分方程组；
[0020]
步骤4-3.利用高阶阻抗边界条件，构造表面电场和磁场的关系式，进而得到等效电流和等效磁流之间的关系式，并将等效磁流用等效电流表示，代入电场积分方程组中；
[0021]
步骤4-4.将电场积分方程组中的等效电流展开系数提取出来，改写为如下矩阵方程：
[0022]
[z][i]＝[v]
[0023]
其中，[z]表示离散后的电场积分方程左端经过伽辽金检验后得到的阻抗矩阵，[i]表示等效电流的展开系数向量，[i]＝[a1,a2,
…
,an]
t
，[v]表示入射电场经过伽辽金检验后得到的电压向量；
[0024]
步骤4-5.当伽辽金检验中的源点和场点间距大于0.15个波长时，利用等效偶极矩方法计算步骤4-4的阻抗矩阵和电压向量，当源点和场点间距小于0.15个波长时，则用矩量法计算步骤4-4的阻抗矩阵和电压向量；进而求解步骤4-4得到的矩阵方程，得到等效电流的展开系数；
[0025]
步骤4-6.利用等效电流的展开系数计算等效电流，根据步骤4-3的等效电流和等效磁流之间的关系式，得到等效磁流及展开系数；
[0026]
步骤5.物理光学区的处理采用物理光学法计算；
[0027]
对po区域采用物理光学法计算，在入射电场照射下，计算po区产生的感应电流和感应磁流，并用rwg基函数展开；
[0028]
步骤6.利用等效偶极矩方法计算mom区和po区的互耦作用；
[0029]
步骤6-1.将步骤4-5得到的mom区的等效电流和等效磁流看作等效电偶极子和等效磁偶极子，利用等效偶极矩方法分别计算等效电偶极子和等效磁偶极子产生的电场和磁场，并将电场和磁场作为po区域耦合的入射场，利用物理光学法计算在该入射场下产生的耦合感应电流和耦合感应磁流，并用rwg基函数展开；
[0030]
步骤6-2.将步骤6-1得到的耦合感应电流和步骤5得到的感应电流看作等效电偶极子，将步骤6-1得到的耦合感应磁流和步骤5得到的感应磁流看作等效磁偶极子，利用等效偶极矩方法分别计算等效电偶极子和等效磁偶极子产生的电场和磁场，将电场和磁场作为mom区的修正入射场，对修正入射场进行伽辽金检验得到修正电压向量[δv]，并对步骤4-4的电压向量进行修正，即令：
[0031]
[v]＝[v]+[δv]
[0032]
执行步骤4-5至步骤4-6得到修正后的mom区的等效电流和等效磁流的展开系数；
[0033]
步骤6-3.判断由步骤6-2得到的修正后mom区的等效电流展开系数和修正前的等效电流展开系数的相对误差，若相对误差小于阈值10-5
，则判定修正后的等效电流和等效磁流即为mom区的真实电流和真实磁流，步骤5得到的po区产生的感应电流与步骤6-1得到的耦合感应电流之和为po区的真实电流，步骤5得到的po区产生的感应磁流与步骤6-1得到的耦合感应磁流之和为po区的真实磁流；若相对误差大于10-5
，则重复步骤6-1至步骤6-3。
[0034]
进一步的，步骤1中，电磁波频率设置为300mhz。
[0035]
进一步的，步骤1中，三角形边长设置为0.1个波长。
[0036]
进一步的，步骤4-1的具体过程为：
[0037]
在mom区域构建散射体模型表面的电场积分方程：
[0038][0039][0040][0041]
其中，j为虚部符号，η0、k0和g分别表示波阻抗、波数和自由空间的格林函数，e
t
为散射体模型表面电场的切向分量，e
inc
表示入射场；s'为r'点所属三角面元对的区域，s为散射体模型表面区域，
·
表示对j(r')求散度，表示对g求梯度，
×
表示求旋度；
[0042]
将用rwg基函数展开后的等效电流和等效磁流代入电场积分方程，得到离散后的电场积分方程：
[0043]
[0044]
进一步的，步骤4-2的电场积分方程组为：
[0045][0046]
其中，fm(r)表示检验rwg基函数，r为fm(r)对应三角面元对的中心位置矢量，1≤m≤n。
[0047]
进一步的，步骤4-3中，表面电场和磁场的关系式为：
[0048][0049][0050][0051]
等效电流和等效磁流之间的关系式：
[0052][0053]
l(q)＝ld(q)-lr(q)
[0054][0055][0056]
其中，q表示向量变量，k'表示介质的波数，a'0、a'1和b'分别为由高阶阻抗边界条件确定的系数，表示散射体模型表面的法向单位向量；下标t表示切向分量。
[0057]
进一步的，步骤4-5中，利用等效偶极矩方法计算步骤4-4的阻抗矩阵的具体过程为：
[0058]
将步骤4-4中的阻抗矩阵表示为：
[0059][0060]
其中，[zj]表示等效电流贡献的部分，[zm]表示等效磁流的贡献，[ze]表示e
t
经过伽辽金检验后形成的矩阵；
[0061][0062][0063]
[0064]
其中，为矩阵[zj]第m行第n列元素，r
mn
表示由第n个rwg基函数中心指向第m个rwg基函数中心的向量，||表示取模，和分别表示第m个和第n个rwg基函数的等效电偶极矩，c＝(1+1/jk0|r
mn
|)/|r
mn
|2；为矩阵[zm]第m行第n列元素，对高阶阻抗边界条件的系数进行泰勒近似，得到
[0065]
进一步的，修正电压向量表示为：
[0066][0067]
其中，表示步骤5中po区产生的感应电流中第i个基函数的展开系数，表示步骤6-1中耦合感应电流中第i个基函数的展开系数，n
p
表示步骤5中基函数的数目，1≤i≤n
p
，第i个rwg基函数的等效电偶极矩，r
mi
由mom区第m个rwg基函数中心指向po区第i个rwg基函数中心的向量，c'＝(1+1/jk0|r
mi
|)/|r
mi
|2。
[0068]
进一步的，对于各向异性介质，由高阶阻抗边界条件，步骤4-3中，等效电流和等效磁流的关系式改写为：
[0069][0070][0071]
其中，和分别是沿着设定各向异性方向的单位向量，k
p
是各向异性介质的波数，j
p
(r')和m
p
(r')分别表示沿各向异性方向的等效电流和等效磁流，和b'
p
分别表示由高阶阻抗边界条件确定的各向异性介质系数；
[0072]
对于p＝1和p＝2，分别执行以下步骤：
[0073]
将等效磁流用等效电流表示，代入电场积分方程组中，执行步骤4-4到步骤6-3。
[0074]
本发明的有益效果是：
[0075]
本发明所述方法利用等效偶极矩方法，不仅加速了mom区阻抗矩阵的填充，还加速了mom和po区的互耦计算，避免了高斯积分中求积阶数对计算速度的影响，大大提高了计算效率；等效偶极矩和物理光学法相结合，通过对目标表面的区域划分，使未知数个数大大减少，同时，引入高阶阻抗边界条件，构造目标表面电磁流的联系，进一步使未知数个数减半，在大幅提高计算效率的同时，还可以极大降低计算机内存占用。并且，该方法应用范围广，适用于pec、各向同性或各向异性介质，对介质涂敷导体目标也同样适用。
附图说明
[0076]
图1为rwg基函数示意图；
[0077]
图2为等效电偶极矩和等效磁偶极矩示意图；
[0078]
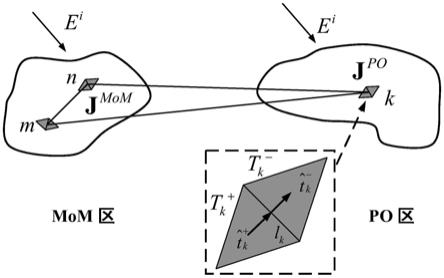
图3为mom和po区域划分示意图；
[0079]
图4为介质涂敷导体球示意图；
[0080]
图5为复合目标示意图。
具体实施方式
[0081]
下面结合附图和实施例对本发明进行进一步的说明。
[0082]
本实施例提供一种基于等效偶极矩和物理光学法的高效电磁散射方法，包括以下步骤：
[0083]
步骤1.在电磁仿真软件中建立散射体模型，设置电磁波频率为300mhz，设置三角形边长为0.1个波长，利用电磁仿真软件对模型表面进行三角形网格划分，导出每个三角形序号和顶点坐标；
[0084]
如图4和图5所示，本实施例的散射体模型选用各向异性介质涂敷导体球与各向异性正方形平板复合目标。pec球体半径为0.48m，表面涂敷一层厚度为0.02m的各向异性介质，介质的相对介电系数为ε
uu
＝4和ε
vv
＝2-j。平板表面的阻抗特性为z
uu
＝2η0和z
vv
＝5η0，主轴偏转角α＝35
°
。
[0085]
步骤2.记录每个三角形的中心坐标及面积，将相邻三角形组成一个三角面元对，编号并记录三角对的个数n，记录每对三角面元对的公共边长度；
[0086]
步骤3.对模型进行分区，将曲率半径大于10个波长的区域划分为物理光学区(po区)，将其他区域划分为矩量区(mom区)；mom和po区域划分示意图如图3所示。
[0087]
步骤4.mom区的处理采用矩量法(mom)计算；
[0088]
将散射体模型的表面等效电流和磁流用rwg基函数离散：
[0089][0090][0091][0092]
其中，j(r')为等效电流，m(r')为等效磁流，r'为散射体模型的表面任意点，1≤n≤n，n为基函数个数(与三角对的个数相同)，fn(r')为第n个rwg基函数，an和bn分别为等效电流和等效磁流中第n个rwg基函数的展开系数；表示第n个三角面元对的正负三角形，
表示第n个三角面元对正负三角形的面积，ln表示第n个三角面元对的公共边长度，表示自由顶点和正负三角形中心所连成的向量；rwg基函数示意图如图1所示。
[0093]
步骤4-1.在mom区域构建散射体模型表面的电场积分方程：
[0094][0095][0096][0097]
其中，j为虚部符号，η0、k0和g分别表示波阻抗、波数和自由空间的格林函数，e
t
为散射体模型表面电场的切向分量，e
inc
表示入射场；s'为r'点所属三角面元对的区域，s为散射体模型表面区域，
·
表示对j(r')求散度，表示对g求梯度，
×
表示求旋度；
[0098]
将用rwg基函数展开后的等效电流和等效磁流代入电场积分方程，得到离散后的电场积分方程：
[0099][0100]
步骤4-2.对离散后的电场积分方程等式两端采用伽辽金检验，即对方程两端同时用n个rwg基函数作内积，将方程个数扩展为n个，得到电场积分方程组：
[0101][0102]
其中，fm(r)表示检验rwg基函数，r为fm(r)对应三角面元对的中心位置矢量，1≤m≤n。
[0103]
步骤4-3.利用高阶阻抗边界条件(hoibc)，构造表面电场和磁场的关系式：
[0104][0105][0106][0107]
进而得到等效电流和等效磁流之间的关系式：
[0108][0109]
l(q)＝ld(q)-lr(q)
[0110][0111][0112]
其中，q表示向量变量，k'表示介质的波数，a'0、a'1和b'分别为由高阶阻抗边界条
件确定的系数，表示散射体模型表面的法向单位向量；下标t表示切向分量；
[0113]
将等效磁流用等效电流表示，代入电场积分方程组中；
[0114]
步骤4-4.通过整理步骤4-3得到的方程组，可将方程组中未知数个数减半，并将等效电流系数提取出来，进而方程组改写为如下形式：
[0115]
[z][i]＝[v]
[0116]
其中，[i]表示等效电流的展开系数向量，[i]＝[a1,a2,
…
,an]
t
，[v]表示入射电场经过伽辽金检验后得到的电压向量；[z]为离散后的电场积分方程左端经过伽辽金检验后得到的阻抗矩阵，表示为：
[0117][0118]
其中，[zj]表示等效电流贡献的部分，[zm]表示等效磁流的贡献，[ze]表示e
t
经过伽辽金检验后形成的矩阵；
[0119]
步骤4-5.当伽辽金检验中的源点和场点间距大于0.15个波长时，利用等效偶极矩方法计算步骤4-4的阻抗矩阵和电压向量，可以避免高斯积分计算中求积阶数的影响；
[0120][0121][0122][0123]
其中，为矩阵[zj]第m行第n列元素，r
mn
表示由第n个rwg基函数中心指向第m个rwg基函数中心的向量，||表示取模，和分别表示第m个和第n个rwg基函数的等效电偶极矩，c＝(1+1/jk0|r
mn
|)/|r
mn
|2；为矩阵[zm]第m行第n列元素，对高阶阻抗边界条件的系数进行泰勒近似，得到等效电偶极矩和等效磁偶极矩示意图如图2所示。
[0124]
当源点和场点间距小于0.15个波长时，则用矩量法计算步骤4-4的阻抗矩阵和电压向量；进而求解步骤4-4得到的矩阵方程，得到等效电流的展开系数；
[0125]
步骤4-6.利用等效电流的展开系数计算等效电流，根据步骤4-3的等效电流和等效磁流之间的关系式，得到等效磁流及展开系数。
[0126]
步骤5.物理光学区的处理采用物理光学法(po)计算；
[0127]
对po区域采用物理光学法计算，在入射电场照射下，计算po区产生的感应电流和感应磁流，并用rwg基函数展开；
[0128]
步骤6.利用等效偶极矩方法(edm)计算mom区和po区的互耦作用；
[0129]
步骤6-1.将步骤4-5得到的mom区的等效电流和等效磁流看作等效电偶极子和等效磁偶极子，利用等效偶极矩方法分别计算等效电偶极子和等效磁偶极子产生的电场和磁场，并将电场和磁场作为po区域耦合的入射场，利用物理光学法计算在该入射场下产生的耦合感应电流和耦合感应磁流，并用rwg基函数展开；
[0130]
步骤6-2.将步骤6-1得到的耦合感应电流和步骤5得到的感应电流看作等效电偶极子，将步骤6-1得到的耦合感应磁流和步骤5得到的感应磁流看作等效磁偶极子，利用等效偶极矩方法分别计算等效电偶极子和等效磁偶极子产生的电场和磁场，将电场和磁场作为mom区的修正入射场，对修正入射场进行伽辽金检验得到修正电压向量[δv]：
[0131][0132]
其中，表示步骤5中po区产生的感应电流中第i个基函数的展开系数，表示步骤6-1中耦合感应电流中第i个基函数的展开系数，n
p
表示步骤5中基函数的数目，1≤i≤n
p
，第i个rwg基函数的等效电偶极矩，r
mi
由mom区第m个rwg基函数中心指向po区第i个rwg基函数中心的向量，c'＝(1+1/jk0|r
mi
|)/|r
mi
|2；
[0133]
对步骤4-4的电压向量进行修正，即令：
[0134]
[v]＝[v]+[δv]
[0135]
重复步骤4-5至步骤4-6得到修正后的mom区的等效电流和等效磁流的展开系数。
[0136]
步骤6-3.判断由步骤6-2得到的修正后mom区的等效电流展开系数和修正前的等效电流展开系数的相对误差，若相对误差小于设定阈值10-5
，则判定修正后的等效电流和等效磁流即为mom区的真实电流和磁流，步骤5得到的po区产生的感应电流与步骤6-1得到的耦合感应电流之和为po区的真实电流，步骤5得到的po区产生的感应磁流与步骤6-1得到的耦合感应磁流之和为po区的真实磁流。若相对误差大于10-5
，则重复步骤6-1至步骤6-3。通常，只需要通过5-10次迭代就能使相对误差小于阈值，从而终止循环。
[0137]
对于各向异性介质，由高阶阻抗边界条件，步骤4-3中，等效电流和等效磁流的关系式改写为：
[0138][0139][0140]
其中，和分别是沿着设定各向异性方向的单位向量，k
p
是各向异性介质的波数，j
p
(r')和m
p
(r')分别表示沿各向异性方向的等效电流和等效磁流，和b'
p
分别表示由高阶阻抗边界条件确定的各向异性介质系数。
[0141]
对于p＝1和p＝2，分别执行以下步骤：
[0142]
将等效磁流用等效电流表示，代入电场积分方程组中，执行步骤4-4到步骤6-3。
[0143]
以上所述，仅为本发明的具体实施方式，本说明书中所公开的任一特征，除非特别叙述，均可被其他等效或具有类似目的的替代特征加以替换；所公开的所有特征、或所有方法或过程中的步骤，除了互相排斥的特征和/或步骤以外，均可以任何方式组合；本领域的技术人员根据本发明技术方案的技术特征所做出的任何非本质的添加、替换，均属于本发明的保护范围。