一种钢-混凝土组合梁抗弯刚度定量识别方法与流程

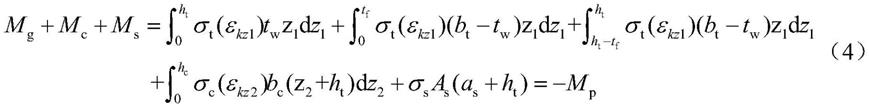
1.本发明属于工程监测技术领域，涉及一种钢-混凝土组合梁抗弯刚度定量识别方法。


背景技术：

2.在桥梁工程和建筑结构中，钢-混凝土组合梁应用的越来越广泛。钢-混凝土组合梁是由钢梁、混凝土板、抗剪连接件组成，钢-混组合梁中抗剪连接件能够有效约束混凝土板与钢梁，形成组合整体，能够充分发挥混凝土抗压强度高、钢梁抗拉强度高的特性，显著提高构件的强度和刚度。抗剪连接件决定了混凝土板与钢梁的协同受力作用效果。抗剪连接件能够传递混凝土板与钢梁交界面的纵向剪力，并且能抑制混凝土板与钢梁竖向分离。钢-组合梁常采用栓钉连接件，栓钉连接件是一种典型的柔性连接件。长期使用中，由于受到各种荷载作用、环境侵蚀、材料老化、自然灾害等种种不利因素的影响，混凝土板和钢梁界面之间会存在滑移、混凝土板会开裂，界面滑移和混凝土开裂会导致钢-混凝土组合梁抗弯刚度下降，承载力降低，变形显著增大，严重时甚至会发生灾难性的事故，造成重大财产及生命损失。因此，对钢-混凝土组合梁在服役期内的抗弯刚度定量识别，显得尤为重要。
3.目前，对钢-混凝土组合梁的抗弯刚度主要采用基于加速度振动测试数据的评估方法，其原理是：通过测量结构的加速度，通过傅里叶变换，识别结构自振频率，而自振频率与结构的抗弯刚度有着一一对应的关系，结构的抗弯刚度下降，会导致自振频率降低。
4.此类方法存在的缺点如下：(1)利用自振频率识别结构抗弯刚度敏感性不足，而且不能考虑结构的非线性；(2)利用自振频率只能识别结构的整体抗弯刚度，不能高精度识别结构局部抗弯刚度；(3)利用自振频率只能定性识别结构的整体抗弯刚度是否变化，不能定量识别结构抗弯刚度。


技术实现要素：

5.本发明要解决的技术问题是针对上述现有技术的不足，而提供一种钢-混凝土组合梁抗弯刚度定量识别方法，该一种钢-混凝土组合梁抗弯刚度定量识别方法为解决上述技术问题，本发明提供如下技术方案：一种钢-混凝土组合梁抗弯刚度定量识别方法，包括以下步骤：
6.s1：将n个长标距应变传感器沿着组合梁长度方向布置在组合梁的底部测量应变，n个长标距应变传感器中其中一个传感器k覆盖的组合梁的区域表示为单元k；
7.s2：将组合梁沿高度方向划分成若干个等厚条带，假定的梁中和轴高度和假定的混凝土板中和轴高度，根据每个假定的梁中和轴高度和假定的混凝土板中和轴高度计算应变，通过材料本构关系计算每个条带的应力；
8.s3：根据应力和条带尺寸计算每个条带的轴力和弯矩，计算总轴力的误差函数，弯矩的误差函数；
9.s4：定义误差指数，当误差指数等于零或取得最小值时，则假定的梁中和轴高度和
假定的混凝土板中和轴高度即为实际中和轴高度；
10.s5：根据钢梁实际中和轴高度，计算单元k的平均曲率；
11.s6：根据弯矩曲率方程，计算单元k的平均抗弯刚度，进而求得任意单元的局部抗弯刚度。
12.优选的，所述步骤s1假定混凝土板，钢梁分别满足平截面假定，具有相同的曲率。
13.优选的，所述步骤s2中：将组合梁沿高度方向划分成若干个等厚条带，采用公式(1)和(2)通过材料本构关系计算每个条带的应力；
14.ε
kz1
＝-ε
k0
z1/h
tk
+ε
k0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
15.其中，ε
kz1
为沿着钢梁高度方向上z1坐标处的应变；h
tk
为梁假定的中和轴高度；ε
k0
为组合梁底部传感器k测取单元k的平均应变；z1为计算位置到钢梁底表面的距离；
16.ε
kz2
＝(h
ck-z2)ε
k0
/h
tk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
17.ε
kz2
为沿着混凝土板高度方向上z2位置处的应变；h
ck
为混凝土板假定的中和轴高度；ε
k0
/h
tk
为钢梁曲率；z2为计算位置到混凝土板底部表面的距离。
18.优选的，所述步骤s3中：根据应力和条带尺寸计算每个条带的轴力和弯矩，计算总轴力的误差函数ef，弯矩的误差函数em，计算公式如下：
[0019][0020]
其中，fg，fc和fs是由钢梁，混凝土板及钢筋产生的轴向力，h
t
和b
t
分别为工字形钢梁的高度和宽度；tw和tf分别为腹板和翼缘厚度，hc和bc分别为混凝土板截面高度和宽度；σ
t
(ε
kz1
)为钢梁应力；σc(ε
kz2
)为混凝土板应力；σs为混凝土板中钢筋的应力；as为混凝土板中钢筋的面积；
[0021][0022]
其中，mc，mg和ms分别是由混凝土板，钢梁和钢筋引起的力矩，m
p
为外部荷载引起的力矩；z1为计算点到钢梁底面的距离；z2为计算点到混凝土板底面的距离；as为钢筋形心到混凝土板底部表面的距离；
[0023][0024][0025]
优选的，所述步骤s4中：为了保证假定的h
tk
和h
ck
同时满足公式(3)和(4)，定义误差指数e
fm
；当e
fm
等于零或取得最小值时，则假定的h
tk
和h
ck
即为实际中和轴高度；
[0026][0027]
优选的，所述步骤s5中：根据钢梁实际中和轴高度h
tk
，计算单元k的平均曲率，公式如下：
[0028][0029]
其中，为单元k的平均曲率。
[0030]
优选的，所述步骤s6中：根据弯矩曲率方程，计算单元k的平均抗弯刚度，公式如下：
[0031][0032]
其中，eik为单元k的平均抗弯刚度。
[0033]
有益效果：(1)本方法采用长标距应变传感器，长标距应变传感器能覆盖组合梁的损伤部位，因此敏感度比基于加速度的方法更高；(2)本方法考虑了钢-混凝土组合梁界面滑移、混凝土材料开裂等非线性因素，因此适用于组合梁受力全过程；(3)本方法不仅可以识别每个单元的局部抗弯刚度，也可以把每个单元的局部抗弯刚度组合成结构整体刚度，由于结构破坏往往是局部先破坏，因此本方法也可以作为一种损伤识别指标；(4)本方法不仅能定性判别组合梁局部抗弯刚度是否发生劣化，而且能定量地识别组合梁局部抗弯刚度。
附图说明
[0034]
图1为钢-混凝土组合梁示意图图；
[0035]
图2为外部荷载下钢-混凝土组合梁变形特征示意图；
[0036]
图3为外部荷载下单元k的应变分析示意图。
具体实施方式
[0037]
下面结合附图和具体较佳实施方式对本发明作进一步详细的说明。
[0038]
本发明的描述中，需要理解的是，术语“左侧”、“右侧”、“上部”、“下部”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，“第一”、“第二”等并不表示零部件的重要程度，因此不能理解为对本发明的限制。本实施例中采用的具体尺寸只是为了举例说明技术方案，并不限制本发明的保护范围。
[0039]
实施例1：
[0040]
参考图1-3，本发明提供一种技术方案，一种钢-混凝土组合梁抗弯刚度定量识别方法，包括以下步骤：
[0041]
s1：将n个长标距应变传感器沿着组合梁长度方向布置在组合梁的底部测量应变，n个长标距应变传感器中其中一个传感器k覆盖的组合梁的区域表示为单元k；
[0042]
s2：将组合梁沿高度方向划分成若干个等厚条带，假定的梁中和轴高度和假定的混凝土板中和轴高度，根据每个假定的梁中和轴高度和假定的混凝土板中和轴高度计算应变，通过材料本构关系计算每个条带的应力；
[0043]
s3：根据应力和条带尺寸计算每个条带的轴力和弯矩，计算总轴力的误差函数，弯矩的误差函数；
[0044]
s4：定义误差指数，当误差指数等于零或取得最小值时，则假定的梁中和轴高度和假定的混凝土板中和轴高度即为实际中和轴高度；
[0045]
s5：根据钢梁实际中和轴高度，计算单元k的平均曲率；
[0046]
s6：根据弯矩曲率方程，计算单元k的平均抗弯刚度，进而求得任意单元的局部抗弯刚度。
[0047]
进一步地，所述步骤s1假定混凝土板，钢梁分别满足平截面假定，具有相同的曲率。
[0048]
进一步地，所述步骤s2中：将组合梁沿高度方向划分成若干个等厚条带，采用公式(1)和(2)通过材料本构关系计算每个条带的应力；
[0049]
ε
kz1
＝-ε
k0
z1/h
tk
+ε
k0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0050]
其中，ε
kz1
为沿着钢梁高度方向上z1坐标处的应变；h
tk
为梁假定的中和轴高度；ε
k0
为组合梁底部传感器k测取单元k的平均应变；z1为计算位置到钢梁底表面的距离；
[0051]
ε
kz2
＝(h
ck-z2)ε
k0
/h
tk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0052]
ε
kz2
为沿着混凝土板高度方向上z2位置处的应变；h
ck
为混凝土板假定的中和轴高度；ε
k0
/h
tk
为钢梁曲率；z2为计算位置到混凝土板底部表面的距离。
[0053]
进一步地，所述步骤s3中：根据应力和条带尺寸计算每个条带的轴力和弯矩，计算总轴力的误差函数ef，弯矩的误差函数em，计算公式如下：
[0054][0055]
其中，fg，fc和fs是由钢梁，混凝土板及钢筋产生的轴向力，h
t
和b
t
分别为工字形钢梁的高度和宽度；tw和tf分别为腹板和翼缘厚度，hc和bc分别为混凝土板截面高度和宽度；σ
t
(ε
kz1
)为钢梁应力；σc(ε
kz2
)为混凝土板应力；σs为混凝土板中钢筋的应力；as为混凝土板中钢筋的面积；
[0056][0057]
其中，mc，mg和ms分别是由混凝土板，钢梁和钢筋引起的力矩，m
p
为外部荷载引起的力矩；z1为计算点到钢梁底面的距离；z2为计算点到混凝土板底面的距离；as为钢筋形心到混凝土板底部表面的距离；
[0058][0059][0060]
进一步地，所述步骤s4中：为了保证假定的h
tk
和h
ck
同时满足公式(3)和(4)，定义误差指数e
fm
；当e
fm
等于零或取得最小值时，则假定的h
tk
和h
ck
即为实际中和轴高度；
[0061]
[0062]
进一步地，所述步骤s5中：根据钢梁实际中和轴高度h
tk
，计算单元k的平均曲率，公式如下：
[0063][0064]
其中，为单元k的平均曲率。
[0065]
进一步地，所述步骤s6中：根据弯矩曲率方程，计算单元k的平均抗弯刚度，公式如下：
[0066][0067]
其中，eik为单元k的平均抗弯刚度。
[0068]
实施例2：
[0069]
参考图1-3，在实施例1的基础上，具体计算过程如下：钢-混凝土组合梁如图1所示；混凝土板和钢梁通过延性抗剪连接件(栓钉)连接。组合梁的跨度和高度分别表示为l和h，假设n根长标距应变传感器分布式布置在组合梁的底部，传感器k覆盖的组合梁区间表示为单元k，如图2所示，假设抗剪连接件的刚度足够大，可认为混凝土板与钢梁交界面不存在界面滑移，在实际的工程中，由于栓钉连接件等大都是延性抗剪连接件，混凝土板和钢梁交界面存在相对滑移(见图2)，通过这种抗剪连接件连接的混凝土组合梁是部分组合作用的，因此这种组合结构并不满足平截面假定。可以合理地假设混凝土板和钢梁均满足平截面假定，并且两者的曲率相同(见图3)。
[0070]
取钢-混凝土组合梁单元k为例，钢梁的中和轴高度为h
tk
，沿着钢梁高度方向上z1坐标处的应变ε
kz1
可以表示为：
[0071]
ε
kz1
＝-ε
k0
z1/h
tk
+ε
k0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0072]
其中，ε
k0
—组合梁底部传感器k测取单元k的平均应变；
[0073]
z1—计算位置到钢梁底表面的距离。
[0074]
如果等式(1)是正值，表示钢梁受拉；如果等式(1)是负值，表示钢梁受压。钢梁曲率为ε
k0
/h
tk
，基于先前假定钢梁与混凝土板具有相同的曲率，可以假设混凝土板中和轴高度为h
ck
，沿着混凝土板高度方向上z2位置处的应变ε
kz2
可以表示为：
[0075]
ε
kz2
＝(h
ck-z2)ε
k0
/h
tk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0076]
其中，z2—计算位置到混凝土板底部表面的距离。
[0077]
如果等式(2)是正值，表示混凝土纤维受拉；如果等式(2)是负值，表示混凝土纤维受压。将等式(1)和(2)分别代入到钢材和混凝土本构关系中，可以获得沿组合梁沿高度方向的应力分布。对于钢-混凝土组合梁单元k，总受拉轴力应等于总受压轴力，分别假设fg，fc和fs是由钢梁，混凝土板及钢筋产生的轴向力。工字形钢梁的高度和宽度分别为h
t
和b
t
，腹板和翼缘厚度分别为tw和tf，混凝土板截面高度和宽度分别为hc和bc。因此，可以获得钢-混组合梁单元k的轴力平衡方程：
[0078]
[0079]
其中，σ
t
(ε
kz1
)—钢梁应力；
[0080]
σc(ε
kz2
)—混凝土板应力；
[0081]
σs—混凝土板中钢筋的应力；
[0082]as
—混凝土板中钢筋的面积。
[0083]
同时，对于钢-混凝土组合梁单元k，内力引起的力矩应该等于外力引起的力矩。假设和mc，mg和ms，分别是由混凝土板，钢梁和钢筋引起的力矩，外部荷载引起的力矩为m
p
，因此，可以获得钢-混凝土组合梁单元k的力矩平衡方程：
[0084][0085]
其中，z1—计算点到钢梁底面的距离；
[0086]
z2—计算点到混凝土板底面的距离；
[0087]as
—钢筋形心到混凝土板底部表面的距离。
[0088]
根据等式(3)和(4)，可以确定钢梁与混凝土板各自的中和轴高度。尽管很难直接求解上述方程式得到h
tk
和h
ck
，但可在每个假设h
tk
和h
ck
的基础上，逐步进行临时计算一直到两个假设值满足等式(3)和(4)为止。首先，钢梁中和轴高度h
tk
和混凝土板中和轴高度h
ck
应该在一定范围内变化。组合梁可以沿梁高度方向切分成诸多恒定厚度的条带，在每个假定的h
tk
和h
ck
条件下，每个条带的应变可以通过等式(1)和(2)获得。然后，每个条带的应力可以通过材料本构关系计算获得。其次，可以根据应力和条带尺寸求得每个条带的轴向力和弯矩。因此，可以将每个条带的轴向力分别求总和获得fg，fc和fs，而不是通过积分计算求得。类似地，mg，mc和ms也可以通过每个条带的力矩求总和来实现。最后，总轴向力的误差函数可以定义为：
[0089][0090]
相似的，总弯矩的误差函数可以表示为：
[0091][0092]
其中ef和em是用来评估假定的h
tk
和h
ck
是否分别满足等式(3)或(4)的参数。如果ef(或em)等于0，就代表h
tk
和h
ck
满足等式(3)(或(4))。为了确保假定的h
tk
和h
ck
均满足等式(3)和(4)，以下指数可以定义为：
[0093][0094]
当e
fm
等于零时或者在钢梁和混凝土板所有假设的中和轴高度中取得最小值时，就能确定实际钢梁中和轴高度h
tk
和混凝土板中和轴高度h
ck
。
[0095]
识别出钢梁和混凝土板中和轴高度h
tk
和h
ck
后，组合梁单元k的平均曲率可以表示为：
[0096]
[0097]
沿着钢-混凝土组合梁长度方向的单元平均抗弯刚度可以表示为：
[0098][0099]
尽管本发明的内容已经通过上述优选实施例作了详细介绍，但应当认识到上述的描述不应被认为是对本发明的限制。在本领域技术人员阅读了上述内容后，对于本发明的多种修改和替代都将是显而易见的。在本发明的技术构思范围内，可以对本发明的技术方案进行多种等同变换，这些等同变换均属于本发明的保护范围。