移动荷载下有吊杆拱桥优化设计方法及系统与流程

1.本发明涉及拱桥设计技术领域，特别涉及移动荷载下有吊杆拱桥优化设计方法及系统。


背景技术：

2.有吊杆拱桥按梁、拱间的受力分担情况可分为两种类型：刚梁柔拱桥、刚拱柔梁桥，刚梁柔拱桥是指主梁的刚度大于主拱的刚度而由主梁承担大部分荷载的桥梁，刚拱柔梁桥是指主拱的刚度大于主梁的刚度而由主拱承担大部分荷载的桥梁。目前使用的有吊杆的拱桥，如附图1所示，其设计过程与一般梁式桥的设计过程有所不同：对于梁式桥梁结构，如果结构尺寸、材料、二期恒载等静力荷载都确定之后，结构的静力荷载内力也随之基本确定，无法进行较大的调整；但对于有吊杆拱桥，由于其成桥线形和内力状态可以通过吊杆张拉力的调整得到，因此有吊杆拱桥设计阶段的主要工作就是确定合理的成桥吊杆力，按合理的成桥吊杆力和常规方法完成其余桥梁构件设计即得到有吊杆拱桥的合理成桥状态。
3.确定合理成桥吊杆力的方法，在悬索桥和斜拉桥中已有较多研究，如中国专利“cn201510312423-一种悬索桥索力优化方法”、“cn202010851156-一种斜拉桥斜拉索优化方法和系统”，及期刊文献“张熙胤,陈兴冲,王常峰.梁拱组合桥吊杆力优化及工程应用[j].铁道建筑,2014,(1).4-6.”、“官华,陈孜伟.梁拱组合桥吊杆成桥初始索力的简化计算方法[j].中外公路,2017,(4).165-170.”、“张玉平,刘雪松,李传习.基于mopso算法的斜拉桥索力优化分析[j].土木与环境工程学报(中英文),2020,(2).107～114.”。
[0004]
现有技术包括刚性吊杆法、刚性支承连续梁法、弯曲应变能最小法、弯矩最小法、弯矩可行域法、零位移法、影响矩阵法、力的平衡法共8类方法，这些方法在悬索桥、斜拉桥和部分有吊杆拱桥中应用时，在仅考虑静力荷载的前提下实现线形、内力状态的优化具有较好的效果；但是，以上方法均是建立在荷载效应的线性叠加基础上进行吊杆力优化的，而移动荷载涉及到影响线分析，影响线分析也是基于荷载效应的线性叠加原理，因此不能在非线性计算中考虑移动荷载的影响线分析，即使不考虑非线性的问题，也因吊杆力优化过程与移动荷载影响线结合难度过大而难以实现，故现有技术在吊杆力优化迭代中放弃考虑移动荷载的作用效应；虽然移动荷载的作用效应相比非移动荷载一般较小，但现有技术放弃考虑移动荷载后所得的吊杆力显然并非最优解，根据移动荷载占桥梁设计总荷载的比例可知，现有技术所得的吊杆力仍有20％～50％范围的优化空间。
[0005]
此外，对于拱桥的稳定性问题，现行规范仅对上承式无吊杆拱桥的平面内稳定给出了线弹性屈曲理论下的验算公式，该公式对于刚拱柔梁桥的平面内稳定问题是近似适用的，但随着梁拱桥梁的推广应用，目前也出现了越来越多的刚梁柔拱桥，这类桥梁的拱截面刚度相对梁截面刚度要小许多，其拱截面高度与拱跨度之比较小，导致拱的线刚度较小，即拱产生单位竖向变形所需要施加的广义力较小，故有吊杆刚梁柔拱桥的非线性效应较强，荷载作用使得主拱偏离合理拱轴线后会带来二阶效应的弯矩，从而显著降低了拱的平面内稳定性，因此该类桥梁的平面内稳定性验算有必要采用非线性屈曲分析方法。而在线性和
非线性屈曲分析时，移动荷载影响线都是不能施加的，现有技术的稳定性分析未能考虑移动荷载作用，且忽视了移动荷载的非对称变形对初始缺陷的影响，与该类桥梁的实际稳定性情况存在较大差异，计算主拱稳定安全系数时存在偏不安全的问题。
[0006]
而对于拱的平面外稳定验算方法，现行规范则并未给出，而对于大部分单肋拱桥，其横桥向线刚度很弱且横桥向无法发挥拱的力学效应，其一阶屈曲模态通常为平面外屈曲，拱肋的稳定安全系数可能会出现远低于强度安全系数的情况，此时的吊杆力起到了一个限制平面外失稳的回复力之作用，吊杆力的优化是改善平面外稳定的有效方式，而现有技术的吊杆力优化方法既未考虑拱的稳定性问题，也未能在其吊杆力优化过程中实现非线性屈曲计算，因此现有技术进行刚梁柔拱桥设计时可能出现其稳定安全系数远低于强度安全系数的不经济性问题，造成材料强度性能未能充分发挥而产生浪费的情况。
[0007]
综上，现有技术至今尚存以下四个方面的问题：
[0008]
1)现有技术的吊杆力优化方法均未能考虑移动荷载的作用效应，导致所得成桥吊杆力并非最优解，仍有20％～50％范围的优化空间；
[0009]
2)现有技术的桥梁稳定性计算中未能考虑移动荷载的作用效应，也忽视了移动荷载可能产生的非对称变形对初始缺陷的影响，与实际稳定性情况存在差异，存在偏不安全的问题；
[0010]
3)现有技术的吊杆力优化方法既未考虑拱桥的稳定性问题，也未能在其吊杆力优化过程中实现非线性屈曲计算，无法兼顾桥梁强度和稳定的综合最优化，可能出现某些拱桥稳定安全系数远低于强度安全系数造成材料强度浪费的问题；
[0011]
4)现有技术的吊杆力优化算法通常按恒定的速度进行迭代优化，未充分结合有吊杆拱桥的力学特性和吊杆力的效应导向来针对性地提高优化算法的性能，难以同时保证优化效果和优化速度，因此在大跨度拱桥的大规模吊杆力优化中需要舍弃一定的优化效果或耗费大量的优化工时。


技术实现要素：

[0012]
为解决现有技术存在的上述四个方面问题，本发明提供了一种移动荷载下有吊杆拱桥优化设计方法及系统，可在有吊杆拱桥设计过程中考虑移动荷载的影响实现桥梁承载力和稳定性的综合最优化，兼顾了桥梁的主拱强度安全系数和稳定安全系数，解出更优的成桥吊杆力，使得设计结果更接近于桥梁实际稳定性情况，避免了出现主拱稳定安全系数远低于强度安全系数的不合理设计问题；同时避免了影响线分析的实现难度和所需的大量用时，并可根据荷载效应来自适应改变优化速度，兼顾了优化效果和优化速度的平衡，采用本发明方法设计的有吊杆拱桥相比现有技术具有更高的经济性，在大跨度拱桥的大规模吊杆力优化中亦能有效应用。
[0013]
为实现上述发明目的，本发明提供了以下技术方案：
[0014]
一种移动荷载下有吊杆拱桥优化设计方法，有吊杆拱桥包括构件：主拱、主梁、吊杆、墩柱和基础，优化设计方法包括以下步骤：
[0015]
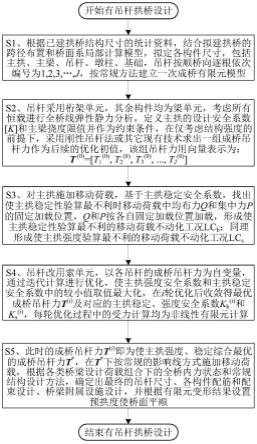
s1、根据已建拱桥结构尺寸的统计资料，结合拟建拱桥的跨径布置和桥面系局部计算模型，拟定各构件尺寸，吊杆按顺桥向逐根依次编号为1,2,3,
…
,j，其中j为自然数，建立一次成桥有限元模型；
[0016]
s2、吊杆采用桁架单元，主拱、主梁、墩柱和基础均采用梁单元，考虑所有恒载进行全桥线弹性静力分析，定义主拱的设计安全系数[k]和主梁挠度限值，并作为约束条件，在仅考虑拱桥结构强度的前提下，求出一组成桥吊杆力，作为优化初值，该组吊杆力用向量表示为：t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；
[0017]
s3、对主拱施加移动荷载，基于主拱稳定安全系数，找出使主拱稳定性验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱稳定性验算最不利的移动荷载不动化工况lcb；同理，对主拱施加移动荷载，基于主拱强度安全系数，找出使主拱强度验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱强度验算最不利的移动荷载不动化工况lcs；
[0018]
s4、吊杆改用索单元，以各吊杆的成桥吊杆力为自变量，通过迭代计算进行优化，使主拱强度安全系数和主拱稳定安全系数中的较小值取值最大化，在i轮迭代后收敛得最优的成桥吊杆力t(i)及对应的主拱稳定安全系数k
b(i)
、强度安全系数k
s(i)
，每轮优化过程中的受力计算均采用非线性有限元计算，i≥0；
[0019]
s5、记成桥吊杆力t(i)为使主拱强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规的影响线方式施加移动荷载，根据桥梁设计荷载组合下的全桥内力状态和常规结构设计方法，确定出最终的吊杆尺寸、各构件的配筋和配束设计、桥梁附属设施设计，并根据有限元变形结果设置预拱度使桥面平顺，结束步骤，得到优化后的有吊杆拱桥设计。
[0020]
本优化设计方法适用的结构形式包括刚梁柔拱桥、刚拱柔梁桥，在上述步骤s1中，不管是刚梁柔拱桥还是刚拱柔梁桥，主梁的尺寸最开始就可基本确定出来：前者多采用先梁后拱施工，主拱主要是起到提升主梁的刚度的作用，多用于铁路桥，主梁截面尺寸一般由主梁恒载和施工阶段受力确定，仅主梁配筋和配束略微受到主拱影响；后者多采用先拱后梁施工，主梁主要起到桥面系的作用并传力至吊杆，其截面尺寸一般由移动荷载的集中力进行局部加载分析后确定，主梁设计基本不受主拱影响。主拱的结构尺寸则可参考已建桥梁的统计资料和主拱拟分担的荷载集度拟定，墩柱、基础的结构尺寸则参考已建桥梁的统计资料和桥梁上部结构的自重再结合恒活载比例确定。吊杆的截面积相对主拱和主梁很小，故虽然吊杆力对桥梁受力影响较大，但吊杆截面本身的大小对桥梁受力影响不大，最终的吊杆截面大小可待吊杆力优化计算完成后再最终确定。
[0021]
通过步骤s1建立有限元模型，通过步骤s2求出成桥吊杆力的优化初值，通过步骤s3施加移动荷载并形成移动荷载的不动化工况，通过步骤s4在计算主拱强度安全系数和稳定安全系数的基础上对成桥吊杆力，进行迭代优化，通过步骤s5记录最优的成桥吊杆力、完成结构设计；步骤s3实现了对移动荷载的不动化，即将移动荷载均布力q和集中力p按固定位置加载，从而在步骤s4的每次迭代优化中均能计入移动荷载进行非线性静力计算和非线性屈曲计算；步骤s4的优化过程计入了移动荷载的影响，从而可获得比现有技术更优的成桥吊杆力，所获吊杆力可使主拱强度和稳定安全系数中的较小值提升20％以上；步骤s4的优化目标兼顾了桥梁主拱的强度安全系数和稳定安全系数，实现了有吊杆拱桥设计时强度和稳定安全性能的综合最优；步骤s5记录了最优的成桥吊杆力，按最优的成桥吊杆力和常规方法完成其余桥梁构件设计，从而得到考虑移动荷载的影响下主拱稳定安全系数与强度安全系数相近的有吊杆拱桥合理成桥状态。
[0022]
在本发明较佳的实施例中，每次执行完上述步骤s4后，按下述步骤优化主拱的构造：
[0023]
s41、在当前主拱的构造下，若min(k
s(i)
,k
b(i)
)》[k]，则转s5；否则，取上一次优化过程的主拱构造及对应的t(i)，转s5；
[0024]
s42、若min(k
s(i)
,k
b(i)
)-[k]》[
△k]，则通过减小主拱截面轮廓尺寸或主拱截面板材厚度来减弱主拱构造，然后转s3，
△k为预设的主拱构造优化收敛精度；否则，转s5。
[0025]
按上述步骤s1～s4对吊杆力优化后，主拱强度和稳定安全系数中的较小值有了较大提升，此时可能会离设计安全系数[k]有较大富余，因此可通过s41～s42步骤对主拱的构造作进一步优化，在满足设计安全系数的前提下减弱主拱构造并结合s3～s4的优化步骤来节省工程造价。
[0026]
在本发明较佳的实施例中，上述步骤s3中形成使主拱稳定性验算最不利的移动荷载不动化工况lcb的具体步骤为：
[0027]
s301、判断主拱构造相比上次优化过程是否有变动，若有则转s302，若无则转s303；
[0028]
s302、修改模型中的主拱单元和截面参数，然后转s304；
[0029]
s303、判断是否当前主拱构造下首次形成工况lcb，若是，则转s304，否则转s311；
[0030]
s304、针对拟建拱桥的一次成桥模型，其索单元修改为桁架单元，施加除移动荷载外的所有桥梁设计荷载，主梁节点按顺桥向逐个编号为1,2,3,
…
,n，进行全桥线弹性静力计算，得到主拱稳定安全系数k
b(0)
；
[0031]
s305、采用蒙特卡罗模拟方法，在吊杆承载力范围内生成m组吊杆力，令吊杆力循环变量m＝1、主梁节点循环变量n＝1，m、n≥1；
[0032]
s306、将有限元模型吊杆力修改为m组吊杆力中第m组的值，若主拱一阶线弹性屈曲非面外失稳，在第n个主梁节点处布置nv个沿截面中心线对称或非对称的单位荷载，并分别建立加载工况，nv为设计车道数；若主拱一阶线弹性屈曲为面外失稳，则在第n个主梁节点处截面中心线的一侧布置nv个单位荷载，并分别建立加载工况，各单位荷载按规范要求的横桥向最小间距布置；
[0033]
s307、进行全桥线弹性屈曲计算，根据1～nv个工况计算结果组合后的最小值，得出主拱稳定安全系数k
b(m,n)
，令k
△
b(m,n)
＝k
b(m,n)-k
b(0)
，k
△
b(m,n)
为移动荷载稳定正负效应矩阵的第m行、第n列个元素；通过k
△
b(m,n)
的正负判断移动荷载稳定正负效应，吊杆力取第m组且移动荷载加载在第n个主梁节点，当移动荷载对桥梁稳定性起到提高作用时，k
△
b(m,n)
为正，即正效应，当移动荷载对桥梁稳定性起到降低作用时，k
△
b(m,n)
为负，即负效应；
[0034]
s308、令n＝n+1，若n》n，则令m＝m+1，转s309；否则，转s306；
[0035]
s309、若m》m，转s310，否则转s306；
[0036]
s310、由s306～s309可得到m行
×
n列的移动荷载稳定正负效应矩阵k
△b，对k
△b逐列求均值后，得稳定影响程度行向量s
b1
，s
b1
反映不同吊杆力水平下移动荷载加载在各主梁节点时对桥梁稳定性加强或减弱的程度；将k
△b统计各列中正值元素个数除以m，得稳定影响显著性行向量s
b2
，s
b2
反映不同吊杆力水平下移动荷载加载在各主梁节点时对桥梁稳定性加强或减弱的概率；s
b1
和s
b2
组成2行
×
n列的稳定敏感线矩阵sb；
[0037]
s311、提取sb各列中第一行小于0且第二行小于所设显著性检验水平αb的列，将移
动荷载中的均布力q加载于所提取列对应的所有主梁节点，将移动荷载中的集中力p加载于所提取列中第一行值最小的主梁节点处，即得使主拱稳定性最不利的移动荷载工况lcb。
[0038]
采用上述步骤s301～s311可实现基于稳定敏感线矩阵进行移动荷载的不动化，即根据移动荷载对主拱稳定的负效应情况将移动荷载均布力q和集中力p按固定位置加载，在形成使主拱稳定性验算最不利的移动荷载不动化工况lcb的过程中，通过蒙特卡罗模拟结合显著性检验，确保了不同吊杆力水平下形成lcb的可靠性，所形成的lcb在拱桥优化过程中各吊杆力发生较大变动时仍能用于加载；形成lcb后，移动荷载不需再按影响线加载来考虑，解决了现有技术存在的因影响线分析无法与屈曲分析或非线性静力计算同时进行，而在吊杆力优化迭代中放弃考虑移动荷载的问题，因此相比现有技术，本发明能得到更优的成桥吊杆力，从而提供更高的桥梁安全性能，并可进一步降低桥梁工程造价；此外，形成lcb后，避免了影响线分析所需的大量用时，在每一次优化迭代中，显著节约了时间成本，保证了大规模优化计算的时间效率。
[0039]
在本发明较佳的实施例中，上述步骤s311完成后，若s306～s309中同一主梁节点处各车道的稳定正负效应不同，修改工况lcb，将该主梁节点处存在负效应且小于所设显著性检验水平αb的车道全部进行移动荷载的均布力q或集中力p加载，得出修改后的工况lcb。
[0040]
相比步骤s301～s311所得的lcb，上述修改后的工况lcb可考虑同一主梁节点处各车道的稳定正负效应不同来进行加载，虽然增加了一部分计算工作量，但修改后的工况lcb产生的主拱稳定负效应更为准确，从而使步骤s4中的吊杆力优化效果进一步提升。
[0041]
在本发明较佳的实施例中，上述步骤s3中形成使主拱强度验算最不利的移动荷载不动化工况lcs的具体步骤为：
[0042]
s321、判断主拱构造相比上次优化过程是否有变动，若有则转s322，若无，则转s323；
[0043]
s322、修改模型中的主拱单元和截面参数，然后转s324；
[0044]
s323、判断是否当前主拱构造下首次形成工况lcs，若是则转s324，否则转s330；
[0045]
s324、针对拟建拱桥的一次成桥模型，其索单元修改为桁架单元，施加除移动荷载外的所有桥梁设计荷载，主梁节点按顺桥向逐个编号为1,2,3,
…
,n，进行全桥线弹性静力计算，得到主拱强度安全系数k
s(0)
；
[0046]
s325、采用蒙特卡罗模拟方法，在吊杆承载力范围内生成m组吊杆力，令吊杆力循环变量m＝1、主梁节点循环变量n＝1；
[0047]
s326、将有限元模型吊杆力修改为m组吊杆力中第m组的值，在第n个主梁节点处布置nv个沿截面中心线对称或非对称的单位荷载，并分别建立加载工况，nv为设计车道数，然后进行全桥线弹性静力计算，根据1～nv个工况计算结果组合后的最小值，得出主拱强度安全系数k
s(m,n)
，令k
△
s(m,n)
＝k
s(m,n)-k
s(0)
；k
△
s(m,n)
为移动荷载强度正负效应矩阵的第m行、n列个元素，通过k
△
b(m,n)
的正负判断移动荷载强度正负效应，吊杆力取第m组且移动荷载加载在第n个主梁节点，当移动荷载对桥梁承载力起到提高作用时，k
△
s(m,n)
为正，即正效应，当移动荷载对桥梁承载力起到降低作用时，k
△
s(m,n)
为负，即负效应；
[0048]
s327、令n＝n+1，若n》n，则令m＝m+1，转s328；否则，转s326；
[0049]
s328、若m》m，转s329，否则转s326；
[0050]
s329、由s326～s328可得到m行
×
n列的移动荷载强度正负效应矩阵k
△s，对k
△s逐列
求均值后，得强度影响程度行向量s
s1
，s
s1
反映不同吊杆力水平下移动荷载加载在各节点时对桥梁承载力加强或减弱的程度；将k
△s统计各列中正值元素个数除以m，得强度影响显著性行向量s
s2
，s
s2
反映不同吊杆力水平下移动荷载加载在各节点时对桥梁承载力加强或减弱的概率；s
s1
和s
s2
组成2行
×
n列的强度敏感线矩阵ss；
[0051]
s330、提取ss各列中第一行小于0且第二行小于所设显著性检验水平αs的列，将移动荷载中的均布力q加载于所提取列对应的所有节点，将移动荷载中的集中力p加载于所提取列中第一行值最小的节点，即得使主拱强度验算最不利的移动荷载不动化工况lcs。
[0052]
采用上述步骤s321～s330可实现基于强度敏感线矩阵进行移动荷载的不动化，在形成使主拱强度验算最不利的移动荷载不动化工况lcs的过程中，通过蒙特卡罗模拟结合显著性检验，确保了不同吊杆力水平下形成lcs的可靠性，所形成的lcs在拱桥优化过程中各吊杆力发生较大变动时，仍能用于加载；形成lcb后，移动荷载不需再按影响线加载来考虑，解决了现有技术存在的因影响线分析无法与屈曲分析或非线性静力计算同时进行，而在吊杆力优化迭代中放弃考虑移动荷载的问题，因此相比现有技术，本发明能得到更优的成桥吊杆力，从而提供更高的桥梁安全性能，并可进一步降低桥梁工程造价；此外，形成lcs后，避免了影响线分析所需的大量用时，在每一次优化迭代中，显著节约了时间成本，保证了大规模优化计算的时间效率。
[0053]
在本发明较佳的实施例中，上述步骤s330完成后，若s326～s328中同一主梁节点处各车道的强度正负效应不同，修改lcb工况，将该主梁节点处存在负效应且小于所设显著性检验水平αs的车道全部进行移动荷载的均布力q或集中力p加载，得出修改后的工况lcs。
[0054]
相比步骤s321～s330所得的lcs，上述修改后的工况lcs可考虑同一主梁节点处各车道的强度正负效应不同来进行加载，虽然增加了一部分计算工作量，但修改后的工况lcb产生的主拱强度负效应更为准确，从而使步骤s4中的吊杆力优化效果进一步提升。
[0055]
在本发明较佳的实施例中，上述步骤s4中对吊杆力迭代优化的具体步骤为：
[0056]
s401、对于n个吊杆力组成的向量x，f(x)代表拱桥各吊杆力按向量x取值时，进行全桥非线性有限元计算所得的主拱强度安全系数ks和主拱稳定安全系数kb中的较小值，计算f(x)时的有限元模型吊杆采用索单元；按成桥吊杆力t
(0)
计算得f(t
(0)
)，其中，t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；令循环变量j＝1；
[0057]
s402、将t
(0)
中的第j个元素的值增加单位力，即t
(0)
变为t
j(0)
，计算得f(t
j(0)
)；若f(t
j(0)
)-f(t
(0)
)》0，则吊杆力优化方向向量d的第个j元素取d(j)＝1，否则令d(j)＝-1；
[0058]
s403、若j《j，则令j＝j+1，转s402；否则，令dj×j＝diag(d)，即形成吊杆力优化方向对角矩阵dj×j，该矩阵反映了仅单根吊杆力增大后对主拱ks和kb中的较小值是起到提升的正效应还是起到降低的负效应，可用于确定后续各根吊杆力的优化方向是优先进行增大还是优先进行减小，然后转s404；
[0059]
s404、以t
(0)
作为优化初值，设定吊杆力变动量的收敛精度ε≥0，吊杆力变动量δ》ε，吊杆力变化的加速系数α≥1，吊杆力变化的减速系数β∈(0,1)；令h1×j为记录各吊杆力变化后相比变化前起到正效应或负效应的变量，对主拱ks和kb中的较小值起到提升作用时为正效应，否则为负效应，其初值为h1×j＝[0,0,0,...,0]；吊杆力优化的外循环变量i＝0，内循环变量j＝1，吊杆力中间变量f
(j)
＝t(i)；
[0060]
s405、令e
(j)
＝d(j,1:j)；若f(f
(j)
+δe
(j)
)》f(t(i))，则h(j)＝1，转s406，否则直接转
s406；
[0061]
s406、若f(f
(j)
+δe
(j)
)》f(f
(j)
)，则令f
(j+1)
＝f
(j)
+δe
(j)
，转s407；否则，令f
(j+1)
＝f
(j)
，转s407；
[0062]
s407、若j《j，则令j＝j+1，转s405；否则，转s408；
[0063]
s408、若各吊杆力按向量f
(j+1)
取值时，主梁的常规设计指标和力学性能满足设计要求，则转s409；否则直接转s412；
[0064]
s409、若f(f
(j+1)
)》f(t(i))，转s410；否则直接转s412；
[0065]
s410、若sum(h)＝j，说明各吊杆力根据dj×j按各自正效应方向变动后对主拱均产生了正效应，即此时桥梁非线性效应不强，故增大吊杆力变动量δ以加快收敛，即令δ＝αδ，然后转s411；否则说明部分吊杆力根据dj×j按其正效应方向变动后对主拱产生了负效应，即此时桥梁非线性效应显著，故不再增大吊杆力变动量δ，而直接转入s411；
[0066]
s411、令t
(i+1)
＝f
(j+1)
；令j＝1，h1×j＝[0,0,0,...,0]，f
(j)
＝t
(i+1)
；i＝i+1，转s405；
[0067]
s412、若δ》ε，令δ＝βδ，减小吊杆力变动量δ来进行精细寻优；令j＝1，h1×j＝[0,0,0,...,0]，f
(j)
＝t(i)，t
(i+1)
＝t(i)，令i＝i+1，转s405；否则说明达到吊杆力变动量的收敛精度，吊杆力优化终止，t(i)即为使主拱强度、主拱稳定综合最优的成桥吊杆力。
[0068]
采用上述步骤s401～s412可实现基于吊杆力效应导向和强度、稳定综合最优的拱桥吊杆力变速迭代优化，该迭代优化方法在桥梁非线性效应不强的阶段具有快速的优化收敛速度，在桥梁非线性效应较强的阶段则具有精细的寻优精度，兼顾了大规模的吊杆力参数优化计算的效率和精度，这是现有的优化算法在吊杆力优化迭代中所不具备的变速优化特征；此外，本算法的优化过程兼顾了桥梁强度和稳定的综合最优，避免了现有技术进行刚梁柔拱桥设计时可能出现其稳定安全系数低于强度安全系数的不经济性问题，采用本算法进行设计可实现稳定安全系数不低于强度安全系数，从而充分发挥了材料的力学性能，不会因稳定性问题造成材料强度浪费。
[0069]
在本发明较佳的实施例中，上述步骤s4中，在每次计算主拱稳定安全系数kb时，按以下步骤进行：
[0070]
s421、判断主拱构造相比上次优化过程是否有变动，若有，则转s422，若无，则转s423；
[0071]
s422、修改模型中的主拱单元和截面参数，然后转s424；
[0072]
s423、判断是否当前主拱构造下首次进行屈曲计算，若是，则转s424，否则转s429；
[0073]
s424、针对拟建拱桥的一次成桥有限元模型，其索单元修改为桁架单元，主拱位置按无初始缺陷时的拱轴线ls0建模，施加除移动荷载外的所有桥梁设计荷载，然后进行全桥线弹性屈曲计算，计算时所有桥梁设计荷载均设为变量；
[0074]
s425、若主拱一阶屈曲为平面外失稳，转s426；否则转s427；
[0075]
s426、静力荷载下主拱线形的初始缺陷幅值δ1为l为主拱计算跨径，主拱初始缺陷线形ls1为其一阶屈曲模态对应的线形按幅值放大至δ1所得线形；然后将移动荷载行驶线按规范允许的最小横桥向间距布于主梁中心线一侧，即移动荷载按单侧偏载布置，顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱线形的初始缺陷幅值δ2，δ2为主拱所有节点的最大横桥向位移值，初始缺陷线形ls2为移动荷载下达到δ2时的主拱横桥向变形后线形；
[0076]
s427、静力荷载下主拱线形的初始缺陷幅值δ1为la为主拱轴线长，为轴压构件稳定系数，初始缺陷线形ls1为一阶屈曲线形按幅值放大至δ1所得线形；然后将移动荷载行驶线横桥向对称布于主梁中心线的两侧，移动荷载顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱线形的初始缺陷幅值δ2，δ2为主拱所有节点的最大竖向位移值，初始缺陷线形ls2为移动荷载下达到δ2时的主拱竖向变形后线形；
[0077]
s428、将主拱节点坐标改为综合初始缺陷线形ls，主拱综合初始缺陷线形ls为ls1和ls2的线性叠加，吊杆改为索单元，移动荷载按步骤s3中移动荷载不动化工况lcb加载，进行非线性屈曲计算，得出非线性屈曲特征值，即主拱的稳定安全系数kb，结束本次稳定安全系数计算。
[0078]
在上述步骤s426中，δ1取是结合主拱的一阶屈曲模态、常规的大跨度钢结构稳定理论和轴压构件受力特性确定的；常规的大跨度钢结构稳定理论认为初始缺陷幅值可取(1/300)
·
l0，l0为框架梁的计算跨径；考虑到主拱的一阶屈曲模态为平面外失稳时，拱的力学效应几乎未能发挥，故可看作为一跨度为l的框架梁失稳问题，l为主拱计算跨径；此外，考虑到主拱发生平面外变形时其轴力也会加剧主拱失稳，故参考轴压构件受力特性理论将l按轴压构件的计算长度系数进行放大，可根据主拱的长细比、端部约束条件结合现行规范查表确定；综上，初始缺陷幅值δ1取在进行屈曲计算时无法对移动荷载进行影响线加载，因此对于δ2的确定，在各类桥梁稳定性计算中现有技术均未作考虑；而移动荷载偏载使主拱产生偏向单侧的水平变形是会实际发生的事情，因此现有技术是偏不安全的。本发明是从稳定问题的基本原理出发，结合移动荷载横桥向单侧偏载作用下主拱必然会发生水平位移的力学特性，偏安全地得出移动荷载下主拱最大横桥向位移达到δ2时的主拱横桥向变形后线形，将其作为移动荷载产生的初始缺陷考虑。综上，同时考虑δ1、δ2对应的线形ls1、ls2作为初始缺陷，可更切实地对主拱的非线性稳定性进行分析。
[0079]
在上述步骤s427中，δ1取是结合主拱的一阶屈曲模态、常规的大跨度钢结构稳定理论和轴压构件受力特性确定的；常规的大跨度钢结构稳定理论认为初始缺陷幅值可取(1/300)
·
l0，l0为框架梁的计算跨径；考虑到主拱的一阶屈曲模态为平面内失稳时，拱的力学效应充分发挥，且平面内一阶屈曲模态为半跨拱下挠、另半跨拱上拱的模态，故可看作为一跨度为(la/2)的框架梁失稳问题，la为主拱的拱轴线长度；此外，考虑到主拱发生平面外变形时其轴力也会加剧主拱失稳，而一般按合理拱轴线设计时主拱的弯矩较小，故参考轴压构件受力特性理论将(la/2)按轴压构件的计算长度系数进行放大，可根据主拱的长细比、端部约束条件结合现行规范查表确定；综上，初始缺陷幅值δ1取在进行屈曲计算时无法对移动荷载进行影响线加载，因此对于δ2的确定，在各类桥梁稳定性计算中，现有技术均未作考虑；而移动荷载偏载使主拱产生半跨下挠、另半跨上拱的水平变形是会实际发生的事情，因此现有技术是偏不安全的。本发明是从稳定问题的基本原理出发，结合移动荷载顺桥向半跨加载作用下主拱必然会发生水平位移的力学特性，偏安全地得出移动荷载影响线分析所得的主拱最大竖向位移达到δ2时的主拱竖向变形后线形，将其作为移动荷载产生的初始缺陷考虑。综上，同时考虑δ1、δ2对应的线形ls1、ls2作为初始缺陷，可更切实地对主拱的非线性稳定性进行分析。
[0080]
采用上述步骤s421～s428可实现考虑移动荷载初始缺陷进行拱桥稳定安全系数
计算，计算过程中能同时考虑静力荷载和移动荷载的影响来确定主拱初始缺陷，可更切实地对主拱的非线性稳定性进行分析，避免了现有技术计算主拱稳定安全系数时因忽略了移动荷载而存在偏不安全的问题。
[0081]
在本发明较佳的实施例中，上述步骤s4中，在每次计算主拱强度安全系数ks时，移动荷载按步骤s3中移动荷载不动化工况lcs加载，ks为主拱受力最不利加载位置处的截面承载力与该截面最不利内力的比值。
[0082]
在每次计算主拱强度安全系数ks时，按移动荷载不动化工况lcs加载，移动荷载不需再按影响线加载来考虑，解决了现有技术因影响线分析无法与非线性静力计算同时进行而在吊杆力优化迭代中放弃考虑移动荷载的问题；同时，避免了影响线分析所需的大量用时，在每一次优化迭代中显著节约了时间成本，保证了大规模优化计算的时间效率。
[0083]
一种移动荷载下有吊杆拱桥优化设计系统，采用上述的移动荷载下有吊杆拱桥优化设计方法，优化设计系统包括建模模块、求吊杆力初值模块、移动荷载加载模块、迭代优化模块和结构设计模块；
[0084]
建模模块用于拟定各构件尺寸、建立一次成桥有限元模型，并将结果输出至求吊杆力初值模块；求吊杆力初值模块用于计算s2中的成桥吊杆力，移动荷载加载模块用于计算出使主拱稳定性验算最不利时移动荷载中均布力q和集中力p的固定加载位置、使主拱强度验算最不利时移动荷载中均布力q和集中力p的固定加载位置，并输出移动荷载不动化工况，迭代优化模块用于计算最优的成桥吊杆力t(i)及对应的主拱稳定安全系数k
b(i)
、强度安全系数k
s(i)
，结构设计模块用于根据主拱强度、稳定综合最优的成桥吊杆力确定出吊杆尺寸、各构件的配筋和配束设计、桥梁附属设施设计。
[0085]
通过该优化设计系统，能够按各模块实现优化设计方法的各步骤，通过建模模块建立成桥有限元模型，通过求吊杆力初值模块获取吊杆力优化初值，通过移动荷载加载模块获取移动荷载的不动化工况，通过迭代优化模块获得最优成桥吊杆力，通过结构设计模块完成最终设计，通过各模块的输出和执行步骤，能够实现有吊杆拱桥设计时强度和稳定安全性能的综合最优，最终完成优化设计。
[0086]
与现有技术相比，本发明的有益效果：
[0087]
1、本发明的优化设计方法，通过步骤s1建立有限元模型，通过步骤s2求出成桥吊杆力的优化初值，通过步骤s3施加移动荷载并形成移动荷载的不动化工况，通过步骤s4在计算主拱强度安全系数和稳定安全系数的基础上对成桥吊杆力进行迭代优化，通过步骤s5记录最优的成桥吊杆力、完成结构设计；步骤s3实现了对移动荷载的不动化，即将移动荷载均布力q和集中力p按固定位置加载，从而在步骤s4的每次迭代优化中均能计入移动荷载进行非线性静力计算和非线性屈曲计算；步骤s4的优化过程计入了移动荷载的影响，从而可获得比现有技术更优的成桥吊杆力，所获吊杆力可使主拱强度和稳定安全系数中的较小值提升20％以上；步骤s4的优化目标兼顾了桥梁主拱的强度安全系数和稳定安全系数，实现了有吊杆拱桥设计时强度和稳定安全性能的综合最优；步骤s5记录了最优的成桥吊杆力，按最优的成桥吊杆力和常规方法完成其余桥梁构件设计，从而得到考虑移动荷载的影响下主拱稳定安全系数与强度安全系数相近的有吊杆拱桥合理成桥状态。
[0088]
2、采用本发明方法步骤s3，可实现基于稳定、强度敏感线矩阵进行移动荷载的不动化，在形成使主拱稳定性和强度验算最不利的移动荷载不动化工况lcb和lcs的过程中，通
过蒙特卡罗模拟并结合显著性检验，确保了不同吊杆力水平下形成lcb和lcs的可靠性，所形成的lcb在拱桥优化过程中各吊杆力发生较大变动时，仍能用于加载；形成lcb和lcs后，移动荷载不需再按影响线加载来考虑，解决了现有技术因影响线分析无法与屈曲分析或非线性静力计算同时进行而在吊杆力优化迭代中放弃考虑移动荷载的问题，相比现有技术能得到更优的成桥吊杆力，从而提供更高的桥梁安全性能，并可进一步降低桥梁工程造价；此外，形成lcb和lcs后，避免了影响线分析所需的大量用时，在每一次优化迭代中显著节约了时间成本，保证了大规模优化计算的时间效率。
[0089]
3、采用本发明方法步骤s4，可实现基于吊杆力效应导向和强度、稳定综合最优的拱桥吊杆力变速优化，该变速优化方法在桥梁非线性效应不强的阶段具有快速的优化收敛速度，在桥梁非线性效应较强的阶段则具有精细的寻优精度，兼顾了大规模的吊杆力参数优化计算的效率和精度，这是现有的优化算法在吊杆力优化过程中所不具备的变速优化特征；此外，本算法的优化过程兼顾了桥梁强度和稳定的综合最优，避免了现有技术进行刚梁柔拱桥设计时可能出现其稳定安全系数远低于强度安全系数的不经济性问题，采用本算法进行设计可实现稳定安全系数不低于强度安全系数，从而充分发挥了材料的力学性能，不会因稳定性问题造成材料强度浪费。
[0090]
4、采用本发明方法步骤s4，可考虑移动荷载初始缺陷进行拱桥稳定安全系数计算，计算过程中能同时考虑静力荷载和移动荷载的影响来确定主拱初始缺陷，可更切实地对主拱的非线性稳定性进行分析，避免了现有技术计算主拱稳定安全系数时因忽略了移动荷载而存在偏不安全的问题。
[0091]
5、本发明的优化设计方法，流程清晰、易于程序化实现，因梁单元和索单元模型的总自由度数较少，结合非线性有限元分析展有吊杆拱桥的大规模设计参数优化仍是可行的，其优化收敛精度亦可根据设计方具有的计算机硬件算力资源灵活确定；算力资源较高时可设置高要求的优化收敛精度，有利于充分发挥高性能计算资源从而得到尽可能最优的设计参数，算力资源较低时可适当降低优化收敛精度的要求，在合理的时间成本下尽可能优化设计参数；因此，本发明方法具有较强的普适性。
[0092]
6、采用本发明的优化设计方法，在相同的工程造价下，本发明设计的有吊杆拱桥相比现有技术具有更高的桥梁安全性能，一般能实现主拱安全性能15％以上的提升，从而降低了桥梁的长期运营维护成本；在相同的安全性能下，本发明设计的有吊杆拱桥相比现有技术具有更低的工程造价，一般能实现主拱和吊杆的综合造价8％以上的降幅，对常见的100～300m跨径的有吊杆拱桥可节约工程造价几十万元至数百万元；考虑到而本发明优化计算花费的时间仅需比现有技术增加数天，数天的时间成本相比整个工程数年的建设周期是很少的，因此优化计算后节省的工程造价所带来的经济效益是相当可观的，采用本发明方法对有吊杆拱桥进行优化设计是非常值得的。
[0093]
7、通过该优化设计系统，通过建模模块建立成桥有限元模型，通过求吊杆力模块获取吊杆力优化初值，通过加载模块获取移动荷载的不动化工况，通过迭代优化模块获得最优成桥吊杆力，通过结构设计模块完成最终设计，通过各模块的输出和执行，按优化设计方法进行，实现优化设计方法的各步骤按严格的程序化流程协调统一地执行，能够实现有吊杆拱桥设计时强度和稳定安全性能的综合最优，最终完成优化设计，提高了对有吊杆拱桥的优化设计效率，节省了人工操作时间。
附图说明
[0094]
图1为本发明的有吊杆拱桥主要构件示意图；
[0095]
图2为本发明的总体步骤图；
[0096]
图3为本发明实施例1中基于稳定敏感线矩阵将移动荷载不动化后形成工况lcb的实施流程图；
[0097]
图4为本发明实施例1的下承式刚梁柔拱桥的有限元模型图；
[0098]
图5为本发明实施例1中使主拱稳定验算最不利的移动荷载不动化工况lcb加载图示的正视图；
[0099]
图6为本发明实施例1中使主拱稳定验算最不利的移动荷载不动化工况lcb加载图示的俯视图；
[0100]
图7为本发明实施例2中基于强度敏感线矩阵将移动荷载不动化后形成工况lcs的实施流程图；
[0101]
图8为本发明实施例2中使主拱强度验算最不利的移动荷载不动化工况lcs加载图示的正视图；
[0102]
图9为本发明实施例2中使主拱强度验算最不利的移动荷载不动化工况lcs加载图示的俯视图；
[0103]
图10为本发明实施例3中考虑移动荷载初始缺陷进行拱桥稳定安全系数计算的实施流程图；
[0104]
图11为本发明实施例3的下承式刚拱柔梁桥的有限元模型图；
[0105]
图12为本发明实施例3的桥梁一阶屈曲模态图；
[0106]
图13为本发明实施例3中主拱初始缺陷线形ls2的正视图；
[0107]
图14为本发明实施例3中主拱综合初始缺陷线形ls的正视图；
[0108]
图15为本发明实施例3中使主拱稳定验算最不利的移动荷载不动化工况lcb加载图示的正视图；
[0109]
图16为本发明实施例4的总体步骤图；
[0110]
图17为本发明实施例4的中承式刚梁柔拱桥的有限元模型图；
[0111]
图18为本发明实施例4的桥梁一阶屈曲模态图；
[0112]
图19为本发明实施例4中使主拱稳定验算最不利的移动荷载不动化工况lcb加载图示的正视图；
[0113]
图20为本发明实施例4中使主拱稳定验算最不利的移动荷载不动化工况lcb加载图示的俯视图；
[0114]
图21为本发明实施例4中使主拱强度验算最不利的移动荷载不动化工况lcs加载图示的正视图；
[0115]
图22为本发明实施例4中使主拱强度验算最不利的移动荷载不动化工况lcs加载图示的俯视图；
[0116]
图23为本发明实施例4中主拱综合初始缺陷线形ls的俯视图；
[0117]
图24为本发明实施例5中基于吊杆力效应导向和强度、稳定综合最优进行拱桥吊杆力变速迭代优化的实施流程图；
[0118]
图25为本发明实施例5中成桥吊杆力迭代优化计算的收敛过程图；
[0119]
图26为本发明实施例6中移动荷载下有吊杆拱桥优化设计系统的示意图；
[0120]
图中标记：1-主梁，2-主拱，3-吊杆，4-墩柱，5-基础，6-q的作用范围，7-p的作用点。
具体实施方式
[0121]
下面结合试验例及具体实施方式对本发明作进一步的详细描述。但不应将此理解为本发明上述主题的范围仅限于以下的实施例，凡基于本发明内容所实现的技术均属于本发明的范围。
[0122]
实施例1
[0123]
请参照图3～图4，本实施例以某跨径布置为(90+180+90)m的拟建下承式刚梁柔拱桥(有吊杆拱桥)为例，该有吊杆拱桥包括构件：主拱2、主梁1、吊杆3、墩柱4和基础5，提供一种移动荷载下有吊杆拱桥优化设计方法，并详细阐述该桥优化设计过程中涉及的基于稳定敏感线矩阵进行移动荷载不动化的过程。
[0124]
请参照图2、图3～图6，该优化设计方法包括以下步骤：
[0125]
s1、根据已建拱桥结构尺寸的统计资料，结合拟建拱桥的跨径布置和桥面系局部计算模型，拟定各构件尺寸，吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j，建立一次成桥有限元模型；
[0126]
具体地，本桥主拱2为钢管混凝土拱，按现有技术确定初始主拱拱2构造尺寸及其它主要构件的构造尺寸，其中主拱2截面为哑铃型截面，建立一次成桥模型见图4；吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j；j＝18；
[0127]
s2、吊杆3采用桁架单元，主拱2、主梁1、墩柱4和基础5均采用梁单元，考虑所有恒载进行全桥线弹性静力分析，定义主拱2的设计安全系数[k]和主梁1挠度限值，并作为约束条件，在仅考虑拱桥结构强度的前提下，求出一组成桥吊杆力，作为优化初值，该组吊杆力用向量表示为：t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；
[0128]
具体地，主拱2的设计安全系数[k]＝1.2，主梁1挠度限值按规范要求取值，按现有技术刚性吊杆法得到成桥吊杆力t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
18(0)
]＝[1160,1386,1177,2005,1594,2451,1930,1347,2123,2123,1347,1930,2451,1594,2005,1177,1386,1160]，单位kn，t
(0)
即作为后续的吊杆力优化初值。
[0129]
s3、对主拱2施加移动荷载，基于主拱2稳定安全系数，找出使主拱2稳定性验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb；同理，对主拱2施加移动荷载，基于主拱2强度安全系数，找出使主拱2强度验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱2强度验算最不利的移动荷载不动化工况lcs；
[0130]
具体地，所谓移动荷载不动化，即将移动荷载均布力q和集中力p按固定位置加载，该拱桥共2条车道，在2条车道上，均布力q的作用范围6和集中力p的作用点7如图6所示，每条车道360m长，集中力p的作用点7位于各车道的中心处对应的主梁节点；对于上述步骤s3中形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb的具体实现过程，按下述步骤s301～s312进行：
[0131]
s301、判断主拱2构造相比上次优化过程是否有变动，若有则转s302，若无则转s303；
[0132]
s302、修改模型中的主拱2单元和截面参数，然后转s304；
[0133]
具体地，本实施例未对主拱2构造进行优化，故直接转s303。
[0134]
s303、判断是否当前主拱2构造下首次形成工况lcb，若是，则转s304，否则转s311；
[0135]
具体地，本实施例为首次形成工况lcb，故转s304。
[0136]
s304、针对拟建拱桥的一次成桥模型，其索单元修改为桁架单元，施加除移动荷载外的所有桥梁设计荷载，主梁1节点按顺桥向逐个编号为1,2,3,
…
,n，进行全桥线弹性静力计算，得到主拱2稳定安全系数k
b(0)
；
[0137]
具体地，对拟建拱桥的一次成桥模型，主梁1按1m节段均匀划分为360个单元，主梁1节点数n＝361，主梁1节点按顺桥向逐个编号为1,2,3,
…
,361，进行全桥线弹性静力计算，得到不考虑移动荷载下的主拱2强度安全系数k
s(0)
＝1.6465、稳定安全系数k
b(0)
＝1.5512。
[0138]
s305、采用蒙特卡罗模拟方法，在吊杆3承载力范围内生成m组吊杆力，令吊杆力循环变量m＝1、主梁1节点循环变量n＝1，m、n≥1；
[0139]
具体地，本实施例均为线弹性有限元计算，且梁单元和桁架单元的总自由度数较少，因此单次计算的速率很快，综合考虑吊杆3数量和设计精度需要，故m＝10000。
[0140]
s306、将有限元模型吊杆力修改为m组吊杆力中第m组的值，若主拱2一阶线弹性屈曲非面外失稳，在第n个主梁1节点处布置nv个沿截面中心线对称或非对称的单位荷载，并分别建立加载工况，nv为设计车道数；若主拱2一阶线弹性屈曲为面外失稳，则在第n个主梁1节点处截面中心线的一侧布置nv个单位荷载，并分别建立加载工况，各单位荷载按规范要求的横桥向最小间距布置；
[0141]
s307、进行全桥线弹性屈曲计算，根据1～nv个工况计算结果组合后的最小值，得出主拱2稳定安全系数k
b(m,n)
，令k
△
b(m,n)
＝k
b(m,n)-k
b(0)
，k
△
b(m,n)
为移动荷载稳定正负效应矩阵的第m行、第n列个元素；通过k
△
b(m,n)
的正负判断移动荷载稳定正负效应，吊杆力取第m组且移动荷载加载在第n个主梁1节点，当移动荷载对桥梁稳定性起到提高作用时，k
△
b(m,n)
为正，即正效应，当移动荷载对桥梁稳定性起到降低作用时，k
△
b(m,n)
为负，即负效应；
[0142]
具体地，本实施例主拱2一阶线弹性屈曲为面外失稳，因桥梁设计车道数为nv＝2条，车道数在截面中心线的单侧按规范要求的横桥向最小间距布置，即每次对第m组吊杆力下的第n个节点进行全桥线弹性屈曲计算前，布置两个在节点单侧的单位荷载，每个荷载的力为10kn、方向竖直向下，各荷载单独对应1个荷载工况，进行全桥线弹性屈曲计算后，取1～2条车道上单位荷载加载工况结果组合后的最小值：即取仅第1条车道加载、仅第2条车道加载、第1和第2条车道都加载这三种情况下的主拱2稳定安全系数最小的值作为k
b(m,n)
，然后计算k
△
b(m,n)
。
[0143]
s308、令n＝n+1，若n》n，则令m＝m+1，转s309；否则，转s306；
[0144]
s309、若m》m，转s310，否则转s306；
[0145]
s310、由s306～s309可得到m行
×
n列的移动荷载稳定正负效应矩阵k
△b，对k
△b逐列求均值后，得稳定影响程度行向量s
b1
，s
b1
反映不同吊杆力水平下移动荷载加载在各主梁1节点时对桥梁稳定性加强或减弱的程度；将k
△b统计各列中正值元素个数除以m，得稳定影响显著性行向量s
b2
，s
b2
反映不同吊杆力水平下移动荷载加载在各主梁1节点时对桥梁稳定
性加强或减弱的概率；s
b1
和s
b2
组成2行
×
n列的稳定敏感线矩阵sb；
[0146]
具体地，由s306～s309可得到10000行
×
361列的移动荷载稳定正负效应矩阵k
△b，对k
△b逐列求均值后得稳定影响程度行向量s
b1
，对k
△b统计各列中正值元素个数除以m得稳定影响显著性行向量s
b2
，s
b1
和s
b2
组成2行
×
n列的稳定敏感线矩阵sb，因结果过长，仅列出sb中代表性的结果如下表1。
[0147]
表1稳定敏感线矩阵sb中代表性的结果
[0148]
节点号123...454647...359360361s
s1-6.56e-6-1.31e-5-1.97e-5...-1.16e-3-1.18e-3-1.16e-3...-1.97e-5-1.31e-5-6.56e-6s
s2
0.0000.0000.000...0.0000.0000.000...0.0000.0000.000
[0149]
s311、提取sb各列中第一行小于0且第二行小于所设显著性检验水平αb的列，将移动荷载中的均布力q加载于所提取列对应的所有主梁1节点，将移动荷载中的集中力p加载于所提取列中第一行值最小的主梁1节点处，即得使主拱2稳定性最不利的移动荷载工况lcb；
[0150]
具体地，根据本行业一般的设计精度要求和统计学一般经验，显著性检验水平取αb＝0.05，得使主拱2稳定验算最不利的移动荷载不动化工况lcb，因lcb中加载的节点很多，仅列出代表性的结果如下表2。
[0151]
表2使主拱稳定验算最不利的移动荷载不动化工况lcb的加载节点
[0152]
节点号123...454647...359360361s
b1
《0？是是是是是是是是是是是s
b2
《αb？是是是是是是是是是是是加均布力？是是是是是是是是是是是加集中力？否否否否否是否否否否否
[0153]
s312、若s306～s309中同一主梁1节点处各车道的稳定正负效应不同，修改工况lcb，将该主梁1节点处存在负效应且小于所设显著性检验水平αb的车道全部进行移动荷载的均布力q或集中力p加载，得出修改后的工况lcb；
[0154]
具体地，s306～s309中每个主梁1节点在不同车道处加载时，各车道的负效应均相同，因此未对lcb工况做进一步修改，lcb的最终加载图示详见图5～图6。
[0155]
s4、吊杆3改用索单元，以各吊杆3的成桥吊杆力为自变量，通过迭代计算进行优化，使主拱2强度安全系数和主拱2稳定安全系数中的较小值取值最大化，在i轮迭代后收敛得最优的成桥吊杆力t(i)及对应的主拱2稳定安全系数k
b(i)
、强度安全系数k
s(i)
，每轮优化过程中的受力计算均采用非线性有限元计算，i≥0；
[0156]
具体地，在当前主拱2构造下，在i＝0时，即未进行吊杆力优化迭代时，主拱2强度安全系数k
s(23)
＝1.5386、主拱2稳定安全系数k
b(23)
＝1.2143；经i＝23轮优化后收敛得当前主拱2构造下的最优成桥吊杆力t
(23)
，t
(23)
＝[t
1(23)
,t
2(23)
,t
3(23)
,...,t
18(23)
]＝[1250,1574,1724,1933,1931,1906,1897,1907,1874,1874,1907,1897,1906,1931,1933,1724,1574,1250]，单位kn，此时主拱2强度安全系数k
s(23)
＝1.4137、主拱2稳定安全系数k
b(23)
＝1.4226。
[0157]
上述步骤s4中，在每次计算主拱强度安全系数ks时，移动荷载按步骤s3中移动荷载不动化工况lcs加载，ks为主拱受力最不利加载位置处的截面承载力与该截面最不利内力
的比值；在每次计算主拱稳定安全系数kb时，移动荷载按步骤s3中移动荷载不动化工况lcb加载，然后进行非线性屈曲计算，得出非线性屈曲特征值，即主拱的稳定安全系数kb。
[0158]
s5、记成桥吊杆力t(i)为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规的影响线方式施加移动荷载，根据桥梁设计荷载组合下的全桥内力状态和常规结构设计方法，确定出最终的吊杆3尺寸、各构件的配筋和配束设计、桥梁附属设施设计，并根据有限元变形结果设置预拱度使桥面平顺，结束步骤，得到优化后的有吊杆拱桥设计；
[0159]
具体地，上述步骤s4中的t
(30)
即为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规设计方法确定出最终的吊杆3尺寸、各类混凝土构件配筋和配束设计、桥梁附属设施；分析s4的结果可知，采用本发明方法进行优化设计后，综合考虑强度和稳定后的安全系数相比现有技术从1.2143提高到了1.4137，即主拱2安全性能提高了16.4％。
[0160]
在本实施例中，采用上述步骤s301～s311可实现基于稳定敏感线矩阵进行移动荷载的不动化，即根据移动荷载对主拱2稳定的负效应情况将移动荷载均布力q和集中力p按固定位置加载，在形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb的过程中，通过蒙特卡罗模拟结合显著性检验，确保了不同吊杆力水平下形成lcb的可靠性，所形成的lcb在拱桥优化过程中各吊杆力发生较大变动时仍能用于加载；形成lcb后，移动荷载不需再按影响线加载来考虑，解决了现有技术存在的因影响线分析无法与屈曲分析或非线性静力计算同时进行，而在吊杆力优化迭代中放弃考虑移动荷载的问题，因此相比现有技术，本发明能得到更优的成桥吊杆力，从而提供更高的桥梁安全性能，并可进一步降低桥梁工程造价；此外，形成lcb后，避免了影响线分析所需的大量用时，在每一次优化迭代中，显著节约了时间成本，保证了大规模优化计算的时间效率。
[0161]
实施例2
[0162]
本实施例采用了实施例1的步骤s1～s5，不同之处在于：本实施例以实施例1中跨径布置为(90+180+90)m的拟建下承式刚梁柔拱桥为例，详细阐述该桥优化设计过程中涉及的基于强度敏感线矩阵进行移动荷载不动化的过程。
[0163]
请参照图2、图4、图7～图9，对于上述实施例1的步骤s3中形成使主拱2强度验算最不利的移动荷载不动化工况lcs的具体实现过程，按下述步骤s321～s331进行：
[0164]
s321、判断主拱2构造相比上次优化过程是否有变动，若有则转s322，若无，则转s323；
[0165]
s322、修改模型中的主拱2单元和截面参数，然后转s324；
[0166]
具体地，本实施例未对主拱2构造进行优化，故直接转s323。
[0167]
s323、判断是否当前主拱2构造下首次形成工况lcs，若是则转s324，否则转s330；
[0168]
具体地，本实施例为首次形成工况lcs，故转s324。
[0169]
s324、针对拟建拱桥的一次成桥模型，其索单元修改为桁架单元，施加除移动荷载外的所有桥梁设计荷载，主梁1节点按顺桥向逐个编号为1,2,3,
…
,n，进行全桥线弹性静力计算，得到主拱2强度安全系数k
s(0)
；
[0170]
具体地，拟建拱桥的一次成桥模型见图4，主梁1按1m节段均匀划分为360个单元，主梁1节点数n＝361，主梁1节点按顺桥向逐个编号为1,2,3,
…
,361，进行全桥线弹性静力计算，得到不考虑移动荷载下的主拱2强度安全系数k
s(0)
＝1.6465、稳定安全系数k
b(0)
＝1.5512。
[0171]
s325、采用蒙特卡罗模拟方法，在吊杆3承载力范围内生成m组吊杆力，令吊杆力循环变量m＝1、主梁1节点循环变量n＝1；
[0172]
具体地，本实施例均为线弹性有限元计算，且梁单元和桁架单元的总自由度数较少，因此单次计算的速率很快，综合考虑吊杆3数量和设计精度需要，故m＝10000。
[0173]
s326、将有限元模型吊杆力修改为m组吊杆力中第m组的值，在第n个主梁1节点处布置nv个沿截面中心线对称或非对称的单位荷载，并分别建立加载工况，nv为设计车道数，然后进行全桥线弹性静力计算，根据1～nv个工况计算结果组合后的最小值，得出主拱2强度安全系数k
s(m,n)
，令k
△
s(m,n)
＝k
s(m,n)-k
s(0)
；k
△
s(m,n)
为移动荷载强度正负效应矩阵的第m行、n列个元素，通过k
△
b(m,n)
的正负判断移动荷载强度正负效应，吊杆力取第m组且移动荷载加载在第n个主梁1节点，当移动荷载对桥梁承载力起到提高作用时，k
△
s(m,n)
为正，即正效应，当移动荷载对桥梁承载力起到降低作用时，k
△
s(m,n)
为负，即负效应；
[0174]
具体地，本实施例的桥梁设计车道数为nv＝2条，车道数按沿截面中心线对称布置，即每次对第m组吊杆力下的第n个节点进行全桥线弹性静力计算前，布置两个沿节点对称的单位荷载，每个荷载的力为10kn、方向竖直向下，各荷载单独对应1个荷载工况，进行全桥线弹性静力计算后，取1～2条车道上单位荷载加载工况结果组合后的最小值：即取仅第1条车道加载、仅第2条车道加载、第1和第2条车道都加载这三种情况下的主拱2强度安全系数最小的值作为k
s(m,n)
，然后计算k
△
s(m,n)
。
[0175]
s327、令n＝n+1，若n》n，则令m＝m+1，转s328；否则，转s326；
[0176]
s328、若m》m，转s329，否则转s326；
[0177]
s329、由s326～s328可得到m行
×
n列的移动荷载强度正负效应矩阵k
△s，对k
△s逐列求均值后，得强度影响程度行向量s
s1
，s
s1
反映不同吊杆力水平下移动荷载加载在各节点时对桥梁承载力加强或减弱的程度；将k
△s统计各列中正值元素个数除以m，得强度影响显著性行向量s
s2
，s
s2
反映不同吊杆力水平下移动荷载加载在各节点时对桥梁承载力加强或减弱的概率；s
s1
和s
s2
组成2行
×
n列的强度敏感线矩阵ss；
[0178]
具体地，由s326～s328可得到10000行
×
361列的移动荷载强度正负效应矩阵k
△s，对k
△s逐列求均值后得强度影响程度行向量s
s1
，对k
△s统计各列中正值元素个数除以m得强度影响显著性行向量s
s2
，s
s1
和s
s2
组成2行
×
n列的强度敏感线矩阵ss，因结果过长，仅列出ss中代表性的结果如下表3。
[0179]
表3强度敏感线矩阵ss中代表性的结果
[0180]
节点号12...454647...89...144145146147s
s1-4.86e-5-9.72e-5...-2.10e-3-2.19e-3-2.10e-3...-9.72e-5...-9.72e-5-4.86e-5-4.91e-69.72e-5s
s2
0.0000.000...0.0000.0000.000...0.000...0.0170.0630.1770.523
[0181]
s330、提取ss各列中第一行小于0且第二行小于所设显著性检验水平αs的列，将移动荷载中的均布力q加载于所提取列对应的所有节点，将移动荷载中的集中力p加载于所提取列中第一行值最小的节点，即得使主拱2强度验算最不利的移动荷载不动化工况lcs；
[0182]
具体地，根据本行业一般的设计精度要求和统计学一般经验，显著性检验水平取αs＝0.05，得使主拱2强度验算最不利的移动荷载不动化工况lcs，因lcs中加载的节点很多，仅列出代表性的结果如下表4。
[0183]
表4使主拱强度验算最不利的移动荷载不动化工况lcs的加载节点
[0184]
节点号12...454647...89...144145146147s
s1
《0？是是是是是是是是是是是是否s
s2
《αs？是是是是是是是是是是是否否加均布力？是是是是是是是是是是是否否加集中力？否否否否是否否否否否否否否
[0185]
s331、若s326～s328中同一主梁1节点处各车道的强度正负效应不同，修改lcb工况，将该主梁1节点处存在负效应且小于所设显著性检验水平αs的车道全部进行移动荷载的均布力q或集中力p加载，得出修改后的工况lcs，该拱桥共2条车道，在2条车道上，均布力q的作用范围6和集中力p的作用点7如图9所示，第1条车道取89m，第2条车道取144m，上述范围的2条车道为均布力q的作用范围6，集中力p的作用点7在第1条车道的中心处对应的主梁节点、第2条车道上p的作用点与第1条车道上p的作用点在桥梁长度方向的作用位置相同；
[0186]
具体地，s326～s328中发现第90～145号节点在不同车道处加载时的负效应有所不同，因此对lcs、lcb工况做进一步修改，将各车道中存在负效应且小于所设显著性检验水平的节点全部进行加载，这样2条车道的顺桥向加载范围就有所差异，这也体现了本方法能考虑桥梁的空间效应进行分析，lcs的最终加载图示详见图8～图9。
[0187]
在本实施例中，采用上述步骤s321～s330可实现基于强度敏感线矩阵进行移动荷载的不动化，在形成使主拱2强度验算最不利的移动荷载不动化工况lcs的过程中，通过蒙特卡罗模拟结合显著性检验，确保了不同吊杆力水平下形成lcs的可靠性，所形成的lcs在拱桥优化过程中各吊杆力发生较大变动时，仍能用于加载；形成lcb后，移动荷载不需再按影响线加载来考虑，解决了现有技术存在的因影响线分析无法与屈曲分析或非线性静力计算同时进行，而在吊杆力优化迭代中放弃考虑移动荷载的问题，因此相比现有技术，本发明能得到更优的成桥吊杆力，从而提供更高的桥梁安全性能，并可进一步降低桥梁工程造价；此外，形成lcs后，避免了影响线分析所需的大量用时，在每一次优化迭代中，显著节约了时间成本，保证了大规模优化计算的时间效率。
[0188]
实施例3
[0189]
本实施例采用和实施例1～2相同的有吊杆拱桥的构件，请参照图10～图11，本实施例以某跨径布置为1
×
100m的拟建下承式刚拱柔梁桥为例，提供一种移动荷载下有吊杆拱桥优化设计方法，并详细阐述该桥优化设计过程中涉及的考虑移动荷载初始缺陷进行拱桥稳定安全系数计算的过程。
[0190]
请参照图2、图10～图15，该优化设计方法包括以下步骤：
[0191]
s1、根据已建拱桥结构尺寸的统计资料，结合拟建拱桥的跨径布置和桥面系局部计算模型，拟定各构件尺寸，吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j，建立一次成桥有限元模型；
[0192]
具体地，本桥主拱2为纯钢结构拱，按现有技术确定初始主拱2构造尺寸及其它主要构件的构造尺寸，其中主拱2截面为矩形钢箱截面，建立一次成桥模型见图11；吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j；j＝15；
[0193]
s2、吊杆3采用桁架单元，主拱2、主梁1、墩柱4和基础5均采用梁单元，考虑所有恒载进行全桥线弹性静力分析，定义主拱2的设计安全系数[k]和主梁1挠度限值，并作为约束
条件，在仅考虑拱桥结构强度的前提下，求出一组成桥吊杆力，作为优化初值，该组吊杆力用向量表示为：t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；
[0194]
具体地，主拱2的设计安全系数[k]＝1.2，主梁1挠度限值按规范要求取值，按现有技术刚性吊杆法得到成桥吊杆力t
(0)
，t
(0)
即作为后续的吊杆力优化初值。
[0195]
s3、对主拱2施加移动荷载，基于主拱2稳定安全系数，找出使主拱2稳定性验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb；同理，对主拱2施加移动荷载，基于主拱2强度安全系数，找出使主拱2强度验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱2强度验算最不利的移动荷载不动化工况lcs；
[0196]
具体地，所谓移动荷载不动化，即将移动荷载均布力q和集中力p按固定位置加载，上述步骤s3中形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb的具体实现过程可参照实施例1的步骤s301～s311，形成使主拱2稳定性验算最不利的移动荷载不动化工况lcs的具体实现过程可参照实施例2的步骤s321～s330。
[0197]
s4、吊杆3改用索单元，以各吊杆3的成桥吊杆力为自变量，通过迭代计算进行优化，使主拱2强度安全系数和主拱2稳定安全系数中的较小值取值最大化，在i轮迭代后收敛得最优的成桥吊杆力t(i)及对应的主拱2稳定安全系数k
b(i)
、强度安全系数k
s(i)
，每轮优化过程中的受力计算均采用非线性有限元计算，i≥0，i轮迭代完成后转s5；
[0198]
具体地，在当前主拱2构造下，经i＝19轮优化后收敛得当前主拱2构造下的最优成桥吊杆力t
(19)
，同时得到此时主拱2强度安全系数k
s(19)
、主拱2稳定安全系数k
b(19)
；
[0199]
具体地，上述步骤s4中，在每次计算主拱2稳定安全系数kb时，按以下步骤进行：
[0200]
s421、判断主拱2构造相比上次优化过程是否有变动，若有，则转s422，若无，则转s423；
[0201]
s422、修改模型中的主拱2单元和截面参数，然后转s424；
[0202]
具体地，本实施例未对主拱2构造进行优化，故直接转s423。
[0203]
s423、判断是否当前主拱2构造下首次进行屈曲计算，若是，则转s424，否则转s429；
[0204]
具体地，本实施例为该主拱2构造下首次屈曲计算，故转s424。
[0205]
s424、针对拟建拱桥的一次成桥有限元模型，其索单元修改为桁架单元，主拱2位置按无初始缺陷时的拱轴线ls0建模，施加除移动荷载外的所有桥梁设计荷载，然后进行全桥线弹性屈曲计算，计算时所有桥梁设计荷载均设为变量；
[0206]
具体地，针对拟建拱桥的一次成桥模型，施加的桥梁设计荷载为结构自重、二期恒载、整体变温、索结构张拉力。
[0207]
s425、若主拱2一阶屈曲为平面外失稳，转s426；否则转s427；
[0208]
s426、静力荷载下主拱2线形的初始缺陷幅值δ1为l为主拱2计算跨径，主拱2初始缺陷线形ls1为其一阶屈曲模态对应的线形按幅值放大至δ1所得线形；然后将移动荷载行驶线按规范允许的最小横桥向间距布于主梁1中心线一侧，即移动荷载按单侧偏载布置，顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱2线形的初始缺陷幅值δ2，δ2为主拱2所有节点的最大横桥向位移值，初始缺陷线形ls2为移动荷载下
达到δ2时的主拱2横桥向变形后线形；
[0209]
具体地，本桥一阶屈曲模态见图12，为平面内失稳，故转s427。
[0210]
s427、静力荷载下主拱2线形的初始缺陷幅值δ1为la为主拱2轴线长，为轴压构件稳定系数，初始缺陷线形ls1为一阶屈曲线形按幅值放大至δ1所得线形；然后将移动荷载行驶线横桥向对称布于主梁1中心线的两侧，移动荷载顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱2线形的初始缺陷幅值δ2，δ2为主拱2所有节点的最大竖向位移值，初始缺陷线形ls2为移动荷载下达到δ2时的主拱2竖向变形后线形；
[0211]
具体地，本桥主拱2轴线长la＝104.94m，按两端固结的轴压构件计算得稳定系数故初始缺陷线形ls1为一阶屈曲线形按幅值放大至δ1所得线形；然后将移动荷载行驶线横桥向对称布于主梁1中心线的两侧，移动荷载顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱2所有节点的最大竖向位移值发生在1/4跨附近，主拱2线形的初始缺陷幅值δ2＝0.051m，可见移动荷载产生的初始缺陷δ2的大小相比δ1也是不宜忽略的值，初始缺陷线形ls2为移动荷载下达到δ2时的主拱2竖向变形后线形，见附图13；
[0212]
在上述步骤s427中，δ1取是结合主拱2的一阶屈曲模态、常规的大跨度钢结构稳定理论和轴压构件受力特性确定的；常规的大跨度钢结构稳定理论认为初始缺陷幅值可取(1/300)
·
l0，l0为框架梁的计算跨径；考虑到主拱2的一阶屈曲模态为平面内失稳时，拱的力学效应充分发挥，且平面内一阶屈曲模态为半跨拱下挠、另半跨拱上拱的模态，故可看作为一跨度为(la/2)的框架梁失稳问题，la为主拱2的拱轴线长度；此外，考虑到主拱2发生平面外变形时其轴力也会加剧主拱2失稳，而一般按合理拱轴线设计时主拱2的弯矩较小，故参考轴压构件受力特性理论将(la/2)按轴压构件的计算长度系数进行放大，可根据主拱2的长细比、端部约束条件结合现行规范查表确定；综上，初始缺陷幅值δ1取在进行屈曲计算时无法对移动荷载进行影响线加载，因此对于δ2的确定，在各类桥梁稳定性计算中，现有技术均未作考虑；而移动荷载偏载使主拱2产生半跨下挠、另半跨上拱的水平变形是会实际发生的事情，因此现有技术是偏不安全的。本发明是从稳定问题的基本原理出发，结合移动荷载顺桥向半跨加载作用下主拱2必然会发生水平位移的力学特性，偏安全地得出移动荷载影响线分析所得的主拱2最大竖向位移达到δ2时的主拱2竖向变形后线形，将其作为移动荷载产生的初始缺陷考虑。综上，同时考虑δ1、δ2对应的线形ls1、ls2作为初始缺陷，可更切实地对主拱2的非线性稳定性进行分析。
[0213]
s428、将主拱2节点坐标改为综合初始缺陷线形ls，主拱2综合初始缺陷线形ls为ls1和ls2的线性叠加，吊杆3改为索单元，移动荷载按步骤s3中移动荷载不动化工况lcb加载，进行非线性屈曲计算，得出非线性屈曲特征值，即主拱2的稳定安全系数kb；
[0214]
具体地，本桥主拱2综合初始缺陷线形ls由ls1和ls2对应的节点坐标值按线性叠加得到，ls的形状见附图14；本桥主拱2节点坐标改为综合初始缺陷线形ls后，使主拱2稳定性最不利的移动荷载不动化工况lcb的加载图示见附图15；进行非线性屈曲计算，得出非线性屈曲特征值即本次计算的主拱2稳定安全系数kb，结束本次稳定安全系数计算。
[0215]
s5、记成桥吊杆力t(i)为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常
规的影响线方式施加移动荷载，根据桥梁设计荷载组合下的全桥内力状态和常规结构设计方法，确定出最终的吊杆3尺寸、各构件的配筋和配束设计、桥梁附属设施设计，并根据有限元变形结果设置预拱度使桥面平顺；
[0216]
具体地，上述步骤s4中的t
(19)
即为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规设计方法确定出最终的吊杆3尺寸、各类混凝土构件配筋和配束设计、桥梁附属设施，并根据有限元变形结果设置预拱度使桥面平顺，结束步骤，得到优化后的有吊杆拱桥设计。
[0217]
在本实施例中，采用上述步骤s421～s428可实现考虑移动荷载初始缺陷进行拱桥稳定安全系数计算，计算过程中能同时考虑静力荷载和移动荷载的影响来确定主拱2初始缺陷，可更切实地对主拱2的非线性稳定性进行分析，避免了现有技术计算主拱2稳定安全系数时因忽略了移动荷载而存在偏不安全的问题。
[0218]
实施例4
[0219]
本实施例采用和实施例1～3相同的有吊杆拱桥的构件，请参照图16～图17，本实施例以某跨径布置为(40+40+168+40+40)m的拟建中承式刚梁柔拱桥为例，提供一种移动荷载下有吊杆拱桥优化设计方法。
[0220]
请参照图2、图16～图23，该优化设计方法包括以下步骤：
[0221]
s1、根据已建拱桥结构尺寸的统计资料，结合拟建拱桥的跨径布置和桥面系局部计算模型，拟定各构件尺寸，吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j，建立一次成桥有限元模型；
[0222]
具体地，本桥主拱2为钢结构拱，按现有技术确定初始主拱2构造尺寸及其它主要构件的构造尺寸，其中主拱2截面为矩形钢箱截面，尺寸为宽3000mm
×
高2500mm
×
厚32mm，建立一次成桥模型见图17；吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j；j＝25；
[0223]
在上述步骤s1中，对于刚梁柔拱桥，主梁1的尺寸最开始就可基本确定出来：该桥采用先梁后拱施工，主拱2主要是起到提升主梁1的刚度的作用，主梁1截面尺寸一般由主梁1恒载和施工阶段受力确定，仅主梁1配筋和配束略微受到主拱2的影响；主拱2的结构尺寸则可参考已建桥梁的统计资料和主拱2拟分担的荷载集度拟定，墩柱4、基础5的结构尺寸则参考已建桥梁的统计资料和桥梁上部结构的自重再结合恒活载比例确定；吊杆3的截面积相对主拱2和主梁1很小，故虽然吊杆力对桥梁受力影响较大，但吊杆3截面本身的大小对桥梁受力影响不大，最终的吊杆3截面大小可待吊杆力优化计算完成后再最终确定。
[0224]
s2、吊杆3采用桁架单元，主拱2、主梁1、墩柱4和基础5均采用梁单元，考虑所有恒载进行全桥线弹性静力分析，定义主拱2的设计安全系数[k]和主梁1挠度限值，并作为约束条件，在仅考虑拱桥结构强度的前提下，求出一组成桥吊杆力，作为优化初值，该组吊杆力用向量表示为：t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；
[0225]
具体地，主拱2的设计安全系数[k]＝1.2，主梁1挠度限值按规范要求取值，按现有技术刚性吊杆法得到成桥吊杆力t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
25(0)
]＝[872,907,873,904,843,862,839,852,884,860,863,864,869,864,863,860,884,852,839,862,843,904,873,907,872]，单位kn，t
(0)
即作为后续的吊杆力优化初值。
[0226]
s3、对主拱2施加移动荷载，基于主拱2稳定安全系数，找出使主拱2稳定性验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位
置加载，形成使主拱2稳定性验算最不利的移动荷载不动化工况lcb；同理，对主拱2施加移动荷载，基于主拱2强度安全系数，找出使主拱2强度验算最不利时移动荷载中均布力q的固定加载位置和集中力p的固定加载位置，q和p按固定加载位置加载，形成使主拱2强度验算最不利的移动荷载不动化工况lcs，该拱桥共6条车道，在6条车道上，均布力q的作用范围6和集中力p的作用点7如图20所示，每条车道在桥梁长度方向的作用范围均为328m，上述范围的6条车道为均布力q的作用范围6，集中力p的作用点7在第1条至第5条车道的各车道中心处对应的主梁节点；
[0227]
具体地，所谓移动荷载不动化，即将移动荷载均布力q和集中力p按固定位置加载，步骤s3的具体实现过程可参照实施例1和实施例2；本实施例中，主梁1按1m节段均匀划分为328个单元，主梁1节点数n＝329，主梁1节点按顺桥向逐个编号为1,2,3,
…
,329；基于蒙特卡罗模拟在吊杆3承载力范围内生成m组吊杆力，m＝10000；本桥横断面布置为：3.5m(人行道)+2.5m(非机动车道)+0.5m(分隔带)+11.5m(机动车道)+4m(中央分隔带)+11.5m(机动车道)+0.5m(分隔带)+2.5m(非机动车道+3.5m(人行道)＝40m，因主拱2为单肋拱，确定使主拱2强度验算最不利的移动荷载不动化工况lcs时，车道数按沿截面中心线对称布置；计算得主拱2一阶线弹性屈曲为面外失稳，见图18，故在确定使主拱2稳定性最不利的移动荷载不动化工况lcb时，车道数在截面中心线单侧并按规范要求的横桥向最小间距布置，且因中央分隔带较宽且存在主拱2、吊杆3起到分隔作用，布置偏载车道时不考虑另半幅桥的移动荷载，即不考虑另半幅的汽车荷载、非机动车荷载、人群荷载；最终，按实施例1的步骤s301～s311得出lcb的加载图示见图19～图20，按实施例2的步骤s321～s330得出lcs的加载图示见图21～图22。
[0228]
s4、吊杆3改用索单元，以各吊杆3的成桥吊杆力为自变量，通过迭代计算进行优化，使主拱2强度安全系数和主拱2稳定安全系数中的较小值取值最大化，在i轮迭代后收敛得最优的成桥吊杆力t(i)及对应的主拱2稳定安全系数k
b(i)
、强度安全系数k
s(i)
，每轮优化过程中的受力计算均采用非线性有限元计算，i≥0，然后转s41；
[0229]
具体地，在每次计算主拱强度安全系数ks时，移动荷载按步骤s3中移动荷载不动化工况lcs加载，ks为主拱受力最不利加载位置处的截面承载力与该截面最不利内力的比值；在每次计算主拱稳定安全系数kb时，移动荷载按步骤s3中移动荷载不动化工况lcb加载，然后进行非线性屈曲计算，得出非线性屈曲特征值，即主拱的稳定安全系数kb；
[0230]
具体地，在初始主拱2构造下，经i＝30轮优化后收敛得当前主拱2构造下的最优成桥吊杆力t
(30)
，t
(30)
＝[t
1(30)
,t
2(30)
,t
3(30)
,...,t
25(30)
]＝[1353,1147,1030,982,963,948,920,882,838,786,736,691,675,691,736,786,838,882,920,948,963,982,1030,1147,1353]，单位kn，此时主拱2强度安全系数k
s(30)
＝1.4146、主拱2稳定安全系数k
b(30)
＝1.3977；
[0231]
此外，上述步骤s4中每次计算主拱2稳定安全系数kb时，其具体实现过程见实施例3的步骤s421～s428；本桥一阶屈曲模态见图18，为平面外失稳，本桥主拱2计算跨径l＝168m，按两端固结的轴压构件计算得稳定系数故初始缺陷线形ls1为一阶屈曲线形按幅值放大至δ1所得线形；然后将移动荷载行驶线横桥向对称布于主梁1中心线的单侧并按规范要求的横桥向最小间距布置，且因中央分隔带较宽且存在主拱2、吊杆3起到分隔作用，布置偏载车道时不考虑另半幅桥的移动荷载，即不考虑
另半幅的汽车荷载、非机动车荷载、人群荷载；移动荷载顺桥向则按影响线加载，进行全桥线弹性静力计算，得出移动荷载下主拱2所有节点的最大竖向位移值发生在1/4跨附近，主拱2线形的初始缺陷幅值δ2＝0.193m，可见移动荷载产生的初始缺陷δ2的大小相比δ1也是不宜忽略的值，初始缺陷线形ls2为移动荷载下达到δ2时的主拱2竖向变形后线形；本桥主拱2综合初始缺陷线形ls由ls1和ls2对应的节点坐标值按线性叠加得到，ls的形状见附图23。
[0232]
当执行完步骤s4中的优化过程后，按下述步骤对主拱2的构造进行优化：
[0233]
s41、在当前主拱2的构造下，若min(k
s(i)
,k
b(i)
)》[k]，则转s5；否则，取上一次优化过程的主拱2构造及对应的t(i)，转s5；
[0234]
s42、若min(k
s(i)
,k
b(i)
)-[k]》[
△k]，则通过减小主拱2截面轮廓尺寸或主拱2截面板材厚度来减弱主拱2构造，然后转s3，
△k为预设的主拱2构造优化收敛精度；否则，转s5。
[0235]
具体地，综合考虑设计精度要求和优化计算成本后，取
△k＝0.05；在初始主拱2构造下，min(k
s(i)
,k
b(i)
)-[k]＝1.3977-1.2＝0.1977》[
△k]，可见初始主拱2构造下的安全系数相比实际设计要求还有较高的富余，还可进一步减弱主拱2构造以节省工程造价，故重复按步骤s3～s42对主拱2构造进行节省优化，主拱2构造优化过程如下表5，因钢箱主拱2截面宽度和高度一般已由桥梁横纵断面布置所确定，故主拱2构造优化时仅变动其板厚；由表1可知，因桥梁用钢板厚度无27mm、26mm之规格，新构造下吊杆力按本发明第4次优化时的钢板厚度规格只能取25mm，此时的min(k
s(i)
,k
b(i)
)已不满足[k]大于1.2之要求，故取上一次的主拱2构造作为优化终值，对应的截面尺寸为宽3000mm
×
高2500mm
×
厚28mm，对应的成桥吊杆力t(i)＝t
(30)
＝[t
1(30)
,t
2(30)
,t
3(30)
,...,t
25(30)
]＝[1288,1098,992,952,940,931,909,877,838,791,746,705,693,705,746,791,838,877,909,931,940,952,992,1098,1288]，单位kn，此时min(k
s(i)
,k
b(i)
)＝1.2295》[k]＝1.2，且未超过[k]太多，该优化终值对应的主拱2构造和成桥吊杆力设计值是经济合理的。
[0236]
表5本实施例成桥吊杆力优化计算的部分详细过程
[0237][0238]
s5、记成桥吊杆力t(i)为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规的影响线方式施加移动荷载，根据桥梁设计荷载组合下的全桥内力状态和常规结构设计方法，确定出最终的吊杆3尺寸、各构件的配筋和配束设计、桥梁附属设施设计，并根据有限元变形结果设置预拱度使桥面平顺，结束步骤，得到优化后的有吊杆拱桥设计；
[0239]
具体地，上述步骤s42中的t
(30)
即为使主拱2强度、稳定综合最优的成桥吊杆力t
*
，在t
*
下按常规设计方法确定出最终的吊杆3尺寸、各类混凝土构件配筋和配束设计、桥梁附属设施后，结合表5可知：
[0240]
1)考虑焊缝重量一般按钢结构重量的1.5％计算后，按现有技术所得的初始主拱2
构造的单位长度用钢量为(1+0.015)*(3000*32*2+2500*32*2)/1000/1000*78.5＝28.05t/m，按本发明所得的最终构造则为(1+0.015)*(3000*28*2+2500*28*2)/1000/1000*78.5＝24.54t/m，可见采用本发明后主拱2用钢量相比现有技术降低了12.5％，而经测算采用本发明后吊杆3的总用钢量由680.7t增加至709.3t，增加了约4.2％，主梁1材料用量则基本未有变化；
[0241]
2)按主拱2钢结构部分的拱轴线长度为159.9m，主拱2钢材的预算单价为1.1万元/t，吊杆3钢材的预算单价一般为主拱2钢材的1.6倍，按现有技术所得的主拱2和吊杆3工程造价合计约为28.05*159.9*1.1+680.7*1.1*1.6＝6132万元，按本发明所得的主拱2和吊杆3工程造价合计约为24.54*159.9*1.1+709.3*1.1*1.6＝5565万元，故按本发明方法进行有吊杆拱桥优化设计后可节约工程造价567万元，主拱2和吊杆3的综合造价节约幅度达9.25％；
[0242]
3)综合考虑桥梁各构件的工程量变化情况和安全系数变化情况可知，采用本发明方法进行设计的桥梁工程造价相比现有技术有了显著的降低，而综合考虑强度和稳定后的安全系数相比现有技术还有所提高。
[0243]
实施例5
[0244]
本实施例采用了实施例4的步骤s1～s5，不同之处在于：本实施例以实施例4中跨径布置为(40+40+168+40+40)m的拟建中承式刚梁柔拱桥为例，详细阐述该桥优化设计过程中涉及的基于吊杆力效应导向和强度、稳定综合最优的拱桥吊杆力变速迭代优化的过程。
[0245]
请参照图2、图17、图24～图25，对于上述实施例4的步骤s4中成桥吊杆力迭代优化计算的具体实现过程，按下述步骤s401～s412进行：
[0246]
s401、对于n个吊杆力组成的向量x，f(x)代表拱桥各吊杆力按向量x取值时，进行全桥非线性有限元计算所得的主拱2强度安全系数ks和主拱2稳定安全系数kb中的较小值，计算f(x)时的有限元模型吊杆3采用索单元；按成桥吊杆力t
(0)
计算得f(t
(0)
)，其中，t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
j(0)
]；令循环变量j＝1；
[0247]
具体地，吊杆3按顺桥向逐根依次编号为1,2,3,
…
,j，j＝25；为方便表述和区分，本实施例中吊杆3编号用带圈数字依次表示为：
①
,
②
,
③
,
…
；按现有技术刚性吊杆法得到成桥吊杆力t
(0)
＝[t
1(0)
,t
2(0)
,t
3(0)
,...,t
25(0)
]＝[872,907,873,904,843,862,839,852,884,860,863,864,869,864,863,860,884,852,839,862,843,904,873,907,872]，单位kn，此时全桥非线性有限元计算得主拱2强度安全系数ks＝1.5523、主拱2稳定安全系数kb＝1.1211，故f(t
(0)
)＝1.1211。
[0248]
s402、将t
(0)
中的第j个元素的值增加单位力，即t
(0)
变为t
j(0)
，计算得f(t
j(0)
)；若f(t
j(0)
)-f(t
(0)
)》0，则吊杆力优化方向向量d的第个j元素取d(j)＝1，否则令d(j)＝-1；
[0249]
s403、若j《j，则令j＝j+1，转s402；否则，令dj×j＝diag(d)，即形成吊杆力优化方向对角矩阵dj×j，该矩阵反映了仅单根吊杆力增大后对主拱2的ks和kb中的较小值是起到提升的正效应还是起到降低的负效应，可用于确定后续各根吊杆力的优化方向是优先进行增大还是优先进行减小，然后转s404；
[0250]
具体地，吊杆力优化方向对角矩阵dj×j中各元素的值见下表6，表中单元格值为1代表单根吊杆力增大后对主拱2的ks和kb间的较小值是起到提升的正效应，为-1则说明起到降低的负效应。
[0251]
表6吊杆力优化方向对角矩阵dj×j中各元素的值
[0252]
1000000000000010000000000000100000000000001000000000000010000000000000100000000000001000000000000010000000000000-10000000000000-10000000000000-10000000000000-10000000000000-1
[0253]
s404、以t
(0)
作为优化初值，设定吊杆力变动量的收敛精度ε≥0，吊杆力变动量δ》ε，吊杆力变化的加速系数α≥1，吊杆力变化的减速系数β∈(0,1)；令h1×j为记录各吊杆力变化后相比变化前起到正效应或负效应的变量，对主拱2的ks和kb中的较小值起到提升作用时为正效应，否则为负效应，其初值为h1×j＝[0,0,0,...,0]；吊杆力优化的外循环变量i＝0，内循环变量j＝1，吊杆力中间变量f
(j)
＝t(i)；
[0254]
具体地，综合考虑设计精度要求和优化计算成本后，本实施例设定吊杆力变动量的收敛精度ε＝1kn，吊杆力变动量初值为δ＝4kn，吊杆力变化的加速系数α＝2.0，吊杆力变化的减速系数β＝0.5。
[0255]
s405、令e
(j)
＝d(j,1:j)；若f(f
(j)
+δe
(j)
)》f(t(i))，则h(j)＝1，转s406，否则直接转s406；
[0256]
s406、若f(f
(j)
+δe
(j)
)》f(f
(j)
)，则令f
(j+1)
＝f
(j)
+δe
(j)
，转s407；否则，令f
(j+1)
＝f
(j)
，转s407；
[0257]
s407、若j《j，则令j＝j+1，转s405；否则，转s408；
[0258]
s408、若各吊杆力按向量f
(j+1)
取值时，主梁1的常规设计指标和力学性能满足设计要求，则转s409；否则直接转s412；
[0259]
s409、若f(f
(j+1)
)》f(t(i))，转s410；否则直接转s412；
[0260]
s410、若sum(h)＝j，说明各吊杆力根据dj×j按各自正效应方向变动后对主拱2均产生了正效应，即此时桥梁非线性效应不强，故增大吊杆力变动量δ以加快收敛，即令δ＝αδ，然后转s411；否则说明部分吊杆力根据dj×j按其正效应方向变动后对主拱2产生了负效应，即此时桥梁非线性效应显著，故不再增大吊杆力变动量δ，而直接转入s411；
[0261]
s411、令t
(i+1)
＝f
(j+1)
；令j＝1，h1×j＝[0,0,0,...,0]，f
(j)
＝t
(i+1)
；i＝i+1，转s405；
[0262]
s412、若δ》ε，令δ＝βδ，减小吊杆力变动量δ来进行精细寻优；令j＝1，h1×j＝[0,0,0,...,0]，f
(j)
＝t(i)，t
(i+1)
＝t(i)，令i＝i+1，转s405；否则说明达到吊杆力变动量的收敛精度，吊杆力优化终止，t(i)即为使主拱2强度、主拱2稳定综合最优的成桥吊杆力；
[0263]
具体地，上述步骤s405～s412中，内循环变量j每从1递增至13即完成一轮内循环，
每轮内循环的每次迭代中吊杆力变动量δ为恒定值；外循环变量i每递增1即进行了一次外循环迭代，δ随着外循环的迭代进程和优化收敛进度可以自适应变化；本实施例的成桥吊杆力优化计算过程见表7～表8和图25，因本桥为对称结构，表8中仅列出半跨吊杆力；由图25可知，在i＝1～15时优化收敛速度较快，此后因δ不断减小而进入精细寻优阶段，收敛速度放缓；当i＝30时，δ＝1kn，达到收敛精度ε，当前主拱2构造下的成桥吊杆力优化计算完毕，t
(30)
即为使主拱2强度、稳定综合最优的成桥吊杆力，t
(30)
＝[t
1(30)
,t
2(30)
,t
3(30)
,...,t
25(30)
]＝[1353,1147,1030,982,963,948,920,882,838,786,736,691,675,691,736,786,838,882,920,948,963,982,1030,1147,1353]，单位kn，此时主拱2强度安全系数k
s(30)
＝1.4146、主拱2稳定安全系数k
b(30)
＝1.3977，故f(t
(30)
)＝1.3977，可见按本发明综合考虑移动荷载下强度和稳定综合最优后，桥梁的安全系数相比现有技术的1.1211提高至1.3977，提高幅度达24.7％，相比现有技术有了显著的改善，若实际设计不要求如此高的安全系数则还可进一步减弱主拱2构造以节省工程造价。
[0264]
表7本实施例成桥吊杆力优化计算的总体变化过程
[0265]
外循环变量if(t(i))变动量δ外循环变量if(t(i))变动量δ01.1211—
ꢀꢀꢀ
11.13084161.36073221.15008171.36843231.176116181.36841641.201232191.37421651.225432201.3796861.247632211.3844871.267932221.3844881.286332231.3873891.302732241.38974101.317232251.38974111.329832261.39164121.340432271.39362131.349132281.39552141.355932291.39742151.360732301.39771
[0266]
表8本实施例成桥吊杆力优化计算的部分详细过程
[0267][0268]
[0269]
在本实施例中，采用上述步骤s401～s412可实现基于吊杆力效应导向和强度、稳定综合最优的拱桥吊杆力变速迭代优化，该迭代优化方法在桥梁非线性效应不强的阶段具有快速的优化收敛速度，在桥梁非线性效应较强的阶段则具有精细的寻优精度，兼顾了大规模的吊杆力参数优化计算的效率和精度，这是现有的优化算法在吊杆力优化迭代中所不具备的变速优化特征；此外，本算法的优化过程兼顾了桥梁强度和稳定的综合最优，避免了现有技术进行刚梁柔拱桥设计时可能出现其稳定安全系数低于强度安全系数的不经济性问题，采用本算法进行设计可实现稳定安全系数不低于强度安全系数，从而充分发挥了材料的力学性能，不会因稳定性问题造成材料强度浪费。
[0270]
实施例6
[0271]
本实施例提供一种移动荷载下有吊杆拱桥优化设计系统，优化设计系统能够应用移动荷载下有吊杆拱桥优化设计方法，该优化设计系统可采用实施例1～5中的步骤s1～s5进行优化设计。
[0272]
请参照图26，优化设计系统包括建模模块、求吊杆力初值模块、移动荷载加载模块、初始缺陷加载模块、迭代优化模块、结构设计模块、输入模块、显示模块和存储模块，其中，建模模块、求吊杆力模块、移动荷载加载模块、初始缺陷加载模块、迭代优化模块和结构设计模块分别植入优化设计方法的对应步骤和计算过程，各模块的功能通过软件的模块划分即可实现，存储模块可采用硬件存储器，也可采用虚拟的软件存储模块，输入模块可采用软件中的界面，也可采用硬件，如键盘，而显示模块为硬件，显示模块采用显示器，也可采用显示屏，输入模块用于用户输入数据，存储模块用于储存上述各模块输出的数据，显示模块用于显示步骤s1～s5的结果，各模块能够依步骤执行，完成优化设计。
[0273]
建模模块用于拟定各构件尺寸、建立一次成桥有限元模型，建模模块执行步骤s1，通过输入模块采集已建拱桥结构尺寸的统计资料、各构件尺寸等，并将结果输出至求吊杆力初值模块；求吊杆力初值模块执行步骤s2，用于计算步骤s2中的成桥吊杆力，并将结果输出至移动荷载加载模块和初始缺陷加载模块；加载模块执行步骤s3，加载模块用于计算出使主拱2稳定性验算最不利时移动荷载中均布力q和集中力p的固定加载位置、使主拱2强度验算最不利时移动荷载中均布力q和集中力p的固定加载位置，并输出移动荷载不动化工况至迭代优化模块；迭代优化模块执行步骤s4，迭代优化模块用于计算最优的成桥吊杆力t(i)及对应的主拱稳定安全系数k
b(i)
、强度安全系数k
s(i)
，并将结果输出至结构设计模块；在迭代优化模块执行过程中，每次计算kb时均调用初始缺陷加载模块来修正主拱节点坐标；结构设计模块执行步骤s5，结构设计模块用于根据主拱2强度、稳定综合最优的成桥吊杆力确定出吊杆3尺寸、各构件的配筋和配束设计、桥梁附属设施设计。通过该优化设计系统，能够按各模块实现优化设计方法的各步骤，通过建模模块建立成桥有限元模型，通过求吊杆力初值模块获取吊杆力优化初值，通过移动荷载加载模块获取移动荷载的不动化工况，通过初始缺陷加载模块可准确计算主拱稳定安全系数，通过迭代优化模块获得最优成桥吊杆力，通过结构设计模块完成最终设计，通过各模块的输出和执行步骤，能够实现有吊杆拱桥设计时强度和稳定安全性能的综合最优，最终完成优化设计。
[0274]
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。