一种基于田口算法的无线充电系统参数优化方法

1.本发明涉及一种基于田口算法的无线充电系统参数优化方法，属于无线充电技术领域。


背景技术：

2.参数优化是指满足一系列有关的条件约束下，选择合理的参数在使设计目标达到最优值。常用参数优化算法包括精确寻优法和近似算法。其中，精确寻优法主要包括线性规划、动态规划、整数规划、分支定界法等；近似寻优法主要包括爬山法，贪心法，遗传算法、正交实验法等。由于精确寻优法通常需要较为精确的数学模型，计算复杂性较大，适于求解小规模问题，在工程中往往不实用。近似算法中，爬山法、贪心法等启发式算法同样需要相对精确的数学模型，凭借经验去判断下一步的步长与方向，存在陷入局部最小值的问题。虽然此问题可以通过设计禁忌表得缓解，但会导致计算量大幅度增加，并且禁忌表的设计依赖于数学模型，从而难以在实际工程问题的参数优化中发挥作用。


技术实现要素：

3.本发明的目的是提出一种基于田口算法的无线充电系统参数优化方法，以解决本发明申请要解决的技术问题。
4.一种基于田口算法的无线充电系统参数优化方法，无线充电系统参数优化方法包括以下步骤：
5.s100、选取合适的优化参数与优化目标，优化参数之间无交叉耦合并且确定各变量的取值范围，筛选出各变量的取值点，将其等效为多个水平数；
6.s200、采用拉丁方以及矩阵变换方式构造正交表，若没有完全合适的正交表，选择采用删除法、拟水平法、组合法或并列法改造正交表；
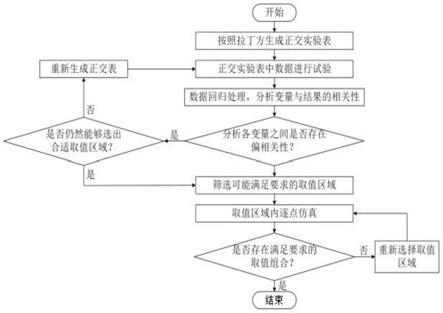
7.s300、处理正交表的实验结果，确定各参数对实验结果的影响方向以及显著性；
8.s400、缩小各参数最优范围的基础上，根据确定的取值范围展开进一步仿真，继续应用正交法，也可在数据点较少的情况下进行穷举法，最终得到满足要求的参数组合。
9.进一步的，在s300中，具体包括以下步骤：
10.s310、按照拉丁方生成正交实验表；
11.s320、将正交实验表中的数据进行试验；
12.s330、进行数据回归处理，分析变量与结果的相关性；
13.s340、分析各变量之间是否存在偏相关性，若是，则执行s350；否则，执行s370；
14.s350、判断是否仍然能够选出合适取值区域，若是，则执行s370；否则，执行s360；
15.s360、重新生成正交表，并返回s320；
16.s370、筛选可能满足要求的取值区域。
17.进一步的，在s400中，具体包括以下步骤：
18.s410、在取值区域内逐点仿真；
19.s420、判断是否存在满足要求的取值组合，若是，则流程结束；否则，执行s430；
20.s430、重新选择取值区域，返回s410。
21.本发明的有以下有益效果：本发明的一种基于田口算法的无线充电系统参数优化方法，通过预先指定正交表的方式最大限度地包含参数取值范围中“均匀分散、齐整可比”的代表点进行试验，分析这部分试验结果的基础上掌握全面试验的情况，探究各因子对实验结果的影响趋势，从而确定符合要求的参数组合。相较于精确寻优法和近似算法，田口算法具有计算量小、易于跳出局部最小值、不依靠精确数学模型等优点。同时，基于田口算法的实验设计是一种基于正交表的、高效率、快速、经济的实验方法，为系统参数优化提供有利支撑。
22.且使用本发明可以有效地降低需要仿真的参数组合的数量，从而大幅度的节省了时间与计算资源，且由于正交标的构造方法已较为成熟，故使用该方法具有方便，快速的优点。
附图说明
23.图1为田口算法的流程图；
24.图2为磁耦合机构示意图；
25.图3为nb0和pianyi散点图。
具体实施方式
26.下面将结合本发明实施例中的附图对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
27.由于无线充电系统的结构复杂性，难以对各参数的影响进行精确建模，从而限制精确算法与部份依赖建模的启发式算法的应用。就依赖于精确数学模型的智能算法(如遗传算法、蚁群算法等)而言，由于这些算法在没有精确数学模型时需要大量、多次的实验，在单次实验耗时较长的无线充电系统的仿真中难以得到良好的应用。同时，由于无线充电系统的参数较多且参数取值范围较广，若使用穷举法进行实验，试验次数过多且计算复杂度过大，难以在工程中得到应用；若使用步长法进行实验，此方法存在对步长变化敏感、依赖使用者经验等问题。
28.针对上述问题，本发明提出田口算法。由于其选择的正交表为纯数学推导，仅为保证每个因子均可参与实验而设计，从而该方案对精确模型无依赖性；由于正交表构造时参数仅包括因子数与每个因子的水平数，该方法最大限度地减少人为测试导致的覆盖率偏低以及冗余测试用例的风险，具备节省时间、控制测试用例数量、保证测试用例覆盖率等优点。
29.参照图1所示，一种基于田口算法的无线充电系统参数优化方法，无线充电系统参数优化方法包括以下步骤：
30.s100、选取合适的优化参数与优化目标，优化参数之间无交叉耦合并且确定各变量的取值范围，筛选出各变量的取值点，将其等效为多个水平数；
31.s200、采用拉丁方以及矩阵变换方式，根据等效的多个水平数构造正交表，若没有完全合适的正交表，选择采用删除法、拟水平法、组合法或并列法改造正交表；
32.s300、处理正交表的实验结果，确定各参数对实验结果的影响方向以及显著性；
33.s400、缩小各参数最优范围的基础上，根据确定的取值范围展开进一步仿真，继续应用正交法，也可在数据点较少的情况下进行穷举法，最终得到满足要求的参数组合。
34.具体的，s100中，优化参数是根据实际的情况进行选取，通常为线圈匝数，无线充电系统的传输距离，线圈与线圈之间的位置关系，线圈内部的匝间距，以及磁芯的大小，位置等。如在下述实施例中，待优化的参数为4个线圈的匝数。
35.而各变量的取值范围，应该按照实际情况构造。比如在无线充电系统的优化中，实际情况就是外观尺寸、线缆的直径、以及传输距离等。
36.进一步的，在s300中，具体包括以下步骤：
37.s310、按照拉丁方生成正交实验表；
38.s320、将正交实验表中的数据进行试验；
39.s330、进行数据回归处理，分析变量与结果的相关性；
40.s340、分析各变量之间是否存在偏相关性，若是，则执行s350；否则，执行s370；
41.s350、判断是否仍然能够选出合适取值区域，若是，则执行s370；否则，执行s360；
42.s360、重新生成正交表，并返回s320；
43.s370、筛选可能满足要求的取值区域。
44.进一步的，在s400中，具体包括以下步骤：
45.s410、在取值区域内逐点仿真；
46.s420、判断是否存在满足要求的取值组合，若是，则流程结束；否则，执行s430；
47.s430、重新选择取值区域，返回s410。
48.以下为本发明的一具体实施例：
49.如图2所示，以无线充电系统中磁耦合机构的偏移性能优化为例，验证本发明提出的田口算法的技术优势。
50.优化参数：发射端线圈a匝数na，接收端线圈a匝数na0；发射端线圈b匝数nb，接收端线圈b匝数nb0，取值范围均为1～19。优化目标：互感值保持11μh左右，0～90mm水平偏移范围内互感值波动不大于
±
5％。每组实验包括10次仿真(0～90mm，10mm为步长)，分析其抗偏移能力以及范围内最小互感值。受限于计算机性能以及正交表生成能力，将每个参数分为9个水平数，代表2匝、4匝、
…
、18匝。使用拉丁方以及矩阵变换构造正交表(l
81
(9
10
))，81组实验涵盖10个9水平数，删除无用变量(6个)并且删除重复行，最终得到正交表(l
81
(94))如正交设计表1所示：
51.正交设计表1
[0052][0053]
正交设计表1
[0054][0055]
正交设计表1
[0056][0057]
表1
[0058]
正交设计表1中，因子1对应na的水平数，因子2对应nb的水平数，因子3对应na0的水平数，因子4对应nb0的水平数。以第一组实验为例，水平数分别为6，2，9，9，根据水平数与匝数的对应关系，水平数表示发射端na，发射端nb，接收端na0，接收端nb0的匝数分别为12、4、18、18。对每组参数组合分别实验，共需要81次实验，其结果整理为表2：
[0059]
[0060]
[0061][0062]
表2中数据按照互感值变化率的倒数降序排列。pianyi表示互感变化率的倒数，hugan表示最小互感大于11μh时互感列设定为1，否则设定为0。由于上述四个变量(na、na0、nb、nb0)之间无相互作用，实验中四个变量可以独立处理。为找出四个变量对目标影响的方向以及显著性，本发明采用分层回归对数据进行分析并且得出如下结论：为达到更佳的抗偏移能力以及较高的互感值，选择较大的na与na0，nb应略小，nb0的选取需进一步讨论。
[0063][0064]
由图3可知：nb和nb0在中间水平数取值时(4～6，对应实际中的8～12匝)具有更强的抗偏移性能。
[0065]
综上所述，多目标优化时应充分考虑变量对结果影响的方向性和显著性。由于na与na0对两参数均有正向影响。进一步优化时，这两个参数取值应适当大一些，尽管nb对抗偏移性能产生显著的负面影响，但其显著性较低并且对互感值影响不大，应适中取值。同理，nb0的取值应当适中。考虑到上文中变量对结果的影响的方向性以及显著性，并结合散点图进行多目标优化后，得出如下两组较为合理的取值范围：
[0066]
第一组：na：14～17，na0：14～17，nb：7～9，nb0：9～11；(na和na0尽量大，nb和nb0取中间值)
[0067]
第二组：na、na0：13～15，nb、nb0：8～12。(考虑到na较大时可能造成nb和nb0影响太小，从而抗偏移性能不佳，na和na0取相对小一些的值(但仍然在较大值范围内)扩大了nb和nb0取值范围)
[0068]
由于区间内数据点较少，使用穷举法对每个组合进行仿真，最终得出一些抗偏移性能较好的参数组合如下：
[0069][0070]
考虑到互感值为11μh左右，本发明选取(13，14，12，12)和(14，13，11，12)两组参数展开对比实验。在速度方面，以cpu i79700@4.5ghz和ansys版本2021r2为例，计算正交表所需数据耗时约6小时(按照每个点计算10组数据分析偏移性能)加上筛选数据时180+225个数据点，总耗时约36小时。若不采用田口算法，按照步长为2对每个变量扫描，数据点总数约6561个，用该计算机仿真耗时约486小时。显然，采用田口算法筛选变量的最佳取值范围有效地节约计算时间与计算负荷。