一种基于随机森林的快递预测方法

1.本发明属于人工智能技术领域，具体涉及一种基于随机森林的快递预测方法。


背景技术：

2.随着社会现代化、信息化的发展，快递平台内部信息化管理所产生的数据量越来越庞大。在人工智能、大数据分析等技术发展的同时，各大单位越来越重视利用智能化产品实现业务管理，利用海量数据提高办理业务效率。然而在现有技术中，尤其是快递平台内部，依旧大量存在办理业务的机械化、盲目性痛点。如何在平台内部利用智能化产品减少人力、物力、财力值得深入研究。另外，当决策者面对海量数据时，如何可以快速找到有效信息，在海量数据中寻找规律，快速掌握影响业务关键特征等重要信息和数据细节，从而避免造成低效甚至错误的研判至关重要。


技术实现要素：

3.针对现有大型单位中快递资源配置如人力、物力和财力浪费的问题，本发明提出了一种基于随机森林的快递预测方法，可以在高速快捷低成本的前提下实现快递单数的预测。为解决以上技术问题，本发明所采用的技术方案如下：
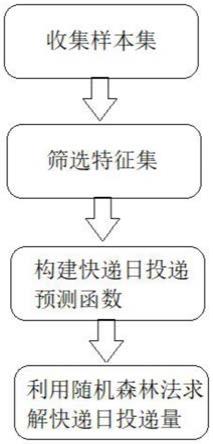
4.一种基于随机森林的快递预测方法，包括如下步骤：
5.s1，收集影响快递单数的历史数据组成样本集；
6.s2，从样本集中筛选出特征数据构成特征集；
7.s3，利用回归预测法构建快递日投递预测函数；
8.s4，利用随机森林方法基于步骤s2所建立的特征集和步骤s3所建立的快递日投递预测函数求解快递日投递量。
9.所述步骤s1包括如下步骤：
10.s1.1，收集某单位若干天内的快递投递数据集；
11.s1.2，采用均值代替法对步骤s1.1收集到的样本集进行清洗；
12.s1.3，根据清洗后的样本集对每天各时间段的快递投递数进行加总计算单位每日投递数。
13.所述特征集中的特征包括订单状态、寄件人部门、寄件人单位。
14.在步骤s3中，所述快递日投递预测函数的表达式为：
[0015][0016]
式中，αn为特征集中特征xn的参数，∈为随机误差，为最终预测的快递日投递量。
[0017]
所述步骤s4包括如下步骤：
[0018]
s4.1，采用bootstrap的方法从样本集的m个样本中随机抽取m个样本作为一个子训练集构建一颗决策树，且m鉠m；
[0019]
s4.2，采用步骤s4.1的方法同步构建t鉠1棵决策树；
[0020]
s4.3，在特征集的n个特征中随机选择p个特征作为节点分裂的子集，根据平方误
差选择p个特征误差最小的1个特征作为节点分裂特征，保持节点分裂直到该决策树不可再分裂，且n鉠p；
[0021]
s4.4，按照步骤s4.3的方法对t棵决策树进行分裂组成随机森林；
[0022]
s4.5，基于快递日投递预测函数对分裂后的每颗决策树随机在m个样本中进行训练得到每颗决策树所对应的快递日投递值；
[0023]
s4.6，对每颗决策树所对应的快递日投递值求取均值得到快递日投递量预测值。
[0024]
本发明的有益效果：
[0025]
本发明主要应用在快递服务平台中，利用特征数据进行模型训练可以实现在高度快捷低成本的前提下对快递单数进行预测，采集随机森林算法实现了日均快递量快速而准确地预测，通过预估计快递单数可以提前对业务做好资源准备；对快递单数预测效果较好，使平台可以更加了解用户特征和需求，进而据此灵活调度快递员和快递车，减少用户投递完成时间，从而节省平台人力和时间成本。
附图说明
[0026]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0027]
图1为现有技术中随机森林的示意图。
[0028]
图2为本发明的预测结果图。
[0029]
图3为基于逻辑回归算法所建立模型的预测结果图。
[0030]
图4为基于最小绝对收缩和选择算法所建立模型的预测结果图。
[0031]
图5为本发明的流程示意图。
具体实施方式
[0032]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0033]
一种基于随机森林的快递预测方法，如图5所示，包括如下步骤：
[0034]
s1，收集影响快递单数的历史数据组成样本集；
[0035]
s1.1，收集某单位若干天内的快递投递数据集；
[0036]
所述快递投递数据集包括寄件人单位、寄件人部门、每天每个时间段下的快递投递数及每个快递的订单状态。寄件人单位也即寄件人的单位名称，寄件人部门是指寄件人所在的部门；订单状态包括是否投递、运输中、订单已完成。
[0037]
s1.2，采用均值代替法对步骤s1.1收集到的样本集进行清洗；
[0038]
所述清洗包括清洗缺失值、清洗与原数据类型不一致的内容、清洗掉不需要的数据，清洗逻辑错误数据。所述逻辑错误数据是指通过简单逻辑推理就可以发现的问题数据。
[0039]
s1.3，根据清洗后的样本集对每天各时间段的快递投递数进行加总得到单位每日
投递数。
[0040]
本实施例中，采用excel整理历史数据，原始数据共7271条数据，10个字段，内容涵盖两个单位，也即单位内部的快递投递和两个单位之间的快递投递，时间跨度为从2021年5月至2021年10月。
[0041]
s2，从样本集中筛选出特征数据构成特征集，所述特征集采用featurei表示，对应的表达式为：
[0042]
featurei＝(x1，x2，
…
，xn)；
[0043]
式中，xn表示特征集中的一个特征，n表示特征集中特征的个数。本实施例中，n＝3,x1为订单状态，x2为寄件人部门，x3为寄件人单位。
[0044]
s3，利用回归预测法构建快递日投递预测函数；
[0045]
所述快递日投递预测函数的表达式为：
[0046][0047]
式中，αn为特征集中特征xn的参数，∈为随机误差，为最终预测的快递日投递量。
[0048]
s4，如图1所示，利用随机森林方法基于步骤s2所建立的特征集和步骤s3所建立的快递日投递预测函数求解快递日投递量，包括如下步骤：
[0049]
s4.1，采用bootstrap的方法从样本集的m个样本中随机抽取m个样本作为一个子训练集构建一颗决策树，且m鉠m；
[0050]
s4.2，采用步骤s4.1的方法同步构建t鉠1棵决策树；
[0051]
s4.3，在特征集的n个特征中随机选择p个特征作为节点分裂的子集，根据平方误差选择p个特征误差最小的1个特征作为节点分裂特征，保持节点分裂直到该决策树不可再分裂；
[0052]
本实施例中，3个特征为根节点和内容节点，单位每日投递数为输出也即叶子节点，且n鉠p。
[0053]
s4.4，按照步骤s4.3的方法对t棵决策树进行分裂组成随机森林；
[0054]
s4.5，基于快递日投递预测函数对分裂后的每颗决策树随机在m个样本中进行训练得到每颗决策树所对应的快递日投递值；
[0055]
s4.6，对每颗决策树所对应的快递日投递值求取均值得到快递日投递量预测值。
[0056]
随机森林包括多个决策树，利用bootstrap想法，即有放回的抽样形成训练集，构建决策树集合。随机森林对训练集中的噪声不敏感，且具有训练速度快的特点，采用随机森林可以将模型并行训练从而提高训练速度，达到快速训练并预测的效果。由于随机森林基于多个决策树，其算法比单个决策树算法更稳健。
[0057]
利用均方误差(mean squared error,mse)和平均绝对误差(meanabsolute error,mae)构建损失函数，通过损失函数判断算法预测与实际数据的差距程度，可以衡量模型的好坏程度。
[0058]
所述均方误差的计算公式如下：
[0059][0060]
式中，l粀ss
m鉠e
表示均方误差损失函数，m表示样本总数，zi表示第i个样本所对应的实际日快递单数；
[0061]
所述平均绝对误差的计算公式如下：
[0062][0063]
式中，l粀ss
m鉠e
表示平均绝对误差损失函数。
[0064]
如图2-图4所示，将本技术与逻辑回归算法(logistic regression,lr)、最小绝对收缩和选择算法(leastabsolute shrinkage and selection operator,lasso)进行对比，如下表1为实验结果对比表，实验证明，本技术在mse和mae指标上取得了最佳的效果。
[0065][0066]
表1实验结果对比
[0067]
寄件人通过快递平台申请快递投递，快递员接单获取快件并配送到指定区域，收件人签收完成订单等功能，将本技术进行应用，以采取上述模式研发的“天津大学综合服务平台”为例，从2019年系统研发至2020年底，截至2020年底，累计订单874份，按每件节省收件人和快递员预约等待时间5分钟计算，合计节省约72小时，大大节省了平台人力和时间成本。
[0068]
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。