量子判别线路及用于渐进训练的模型的制作方法

1.本技术实施例大体上涉及量子计算领域，更具体地，涉及量子判别线路及用于渐进训练的模型。


背景技术：

2.近年来，机器学习已在众多领域中得到了大量的应用。作为人工智能的核心，随着大数据时代各行业对数据分析需求的持续增加，如何基于机器学习对复杂多样的数据进行深层次的分析，更高效地利用信息成为当前大数据环境下机器学习研究的主要方向。为进一步优化传统机器学习，人们对利用量子线路辅助机器学习已开始有所研究。然而，目前的量子判别线路及用于渐进训练的模型相关的研究较少。
3.因此，本技术提出一种量子判别线路及用于渐进训练的模型。


技术实现要素：

4.本技术实施例的目的之一在于提供一种量子判别线路及用于渐进训练的模型，与传统的方法与模型相比，其可减少所使用的参数量，且所用的存储介质，即量子比特数目也大幅减少。
5.本技术的一实施例提供一种量子判别线路，其包括所用量子比特依次减少的多个子线路。
6.本技术的另一实施例提供一种用于渐进训练的模型，其包括上述量子判别线路。
7.本技术的另一实施例还提供一种用于预测病毒变异结构的模型，其包括上述用于渐进训练的模型。
8.本技术的另一实施例还提供一种用于渐进训练模型的生成器，其通过使用上述量子判别线路进行优化以生成待预测的数据。
9.与现有技术相比，本技术实施例提供的量子判别线路及用于渐进训练的模型，利用量子计算对经典计算方式作为替换或补充，可有效提高数据处理速度与准确度。
附图说明
10.在下文中将简要地说明为了描述本技术实施例或现有技术所必要的附图以便于描述本技术的实施例。显而易见地，下文描述中的附图仅只是本技术中的部分实施例。对本领域技术人员而言，在不需要创造性劳动的前提下，依然可以根据这些附图中所例示的结构来获得其他实施例的附图。
11.图1为根据本技术一些实施例的量子判别线路120的示意图。
12.图2为根据本技术一些实施例的量子卷积核uc的示意图。
13.图3为根据本技术一些实施例的量子池化核up的示意图。
14.图4为根据本技术一些实施例的量子稠密核u
dense
的示意图。
15.图5为根据本技术一些实施例的量子模糊卷积核ub的示意图。
16.图6为根据本技术一些实施例的用于渐进训练的模型示意图。
17.图7为根据本技术一些实施例的棘突蛋白序列的部分数据在excel中的表达形式。
18.图8和9为根据本技术一些实施例的经典模型和用于渐进训练的模型优化的对比结果。
具体实施方式
19.为更好的理解本技术实施例的精神，以下结合本技术的部分优选实施例对其作进一步说明。
20.本技术的实施例将会被详细的描示在下文中。在本技术说明书全文中，将相同或相似的组件以及具有相同或相似的功能的组件通过类似附图标记来表示。在此所描述的有关附图的实施例为说明性质的、图解性质的且用于提供对本技术的基本理解。本技术的实施例不应该被解释为对本技术的限制。
21.在对本技术技术方案进行介绍之前，首先对本技术中涉及的一些关键术语进行解释说明：
22.1.量子计算：基于量子逻辑的计算方式，存储数据的基本单元是量子比特。
23.2.量子比特：量子计算的基本单元。传统计算机使用0和1作为二进制的基本单元。不同的是量子计算可以同时处理0和1，使得系统可以处于0和1的线性叠加态：|ψ》＝α|0》+β|1》，这边α，β代表系统在0和1上的复数概率幅。它们的模平方|α|2，|β|2分别代表处于0和1的概率。
24.3.量子线路：量子通用计算机的一种表示，代表了相应量子算法/程序在量子门模型下的硬件实现。若量子线路中包含可调的控制量子门的参数，则被称为参数化的量子线路。
25.4.量子门：常使用矩阵表示，操作n个量子比特的门可以用2
n x 2n的酉矩阵表示。一个门输入跟输出的量子比特数量必须要相等。量子门的操作可以用代表量子门的矩阵与代表量子比特状态的向量作相乘来表示。
26.5.旋转门：旋转门是量子门的一种，是一组三个2
×
2的幺正厄米复矩阵(又称酉矩阵)。其中，旋转x门为旋转y门为旋转y门为旋转z门为
27.6.量子经典混合计算：一种内层利用量子线路进行计算得出相应物理量或损失函数，外层用传统的经典优化器调节量子线路变分参数的计算范式，可以最大限度地发挥量子计算的优势，被相信是有潜力证明量子优势的重要方向之一。
28.本技术提出的量子判别线路及用于渐进训练的模型，通过使用量子线路，有效提高了模型学习能力和运行效率。
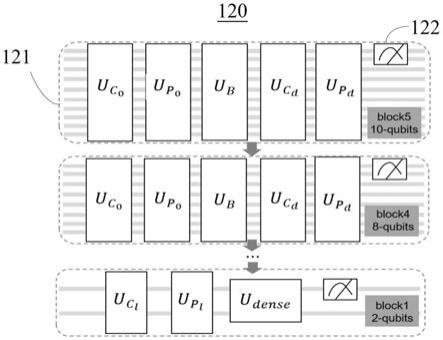
29.图1为根据本技术一些实施例的量子判别线路120的示意图。
30.本技术提出的量子判别线路可包括所用量子比特依次减少的多个子线路，以应用
于需要进行渐进训练的模型的开发与研究。
31.判别线路可对于输入的高维度的数据进行特征提取得到低维度的判别信息，比如实现对数据的分类，检测等等。在某些应用中，可通过判别线路来引导生成器的训练，通过两个模型之间的交替训练不断进行对抗，最终使得生成模型能够更好地完成生成任务。
32.本技术提出的量子判别线路基于量子比特的数据表达能力更优，通过量子计算实现高度并行处理数据的性能。
33.如图1所示，量子判别线路120可包括所用量子比特依次减少的五个子线路121，分别从10量子比特到2量子比特，每个子线路比前一子线路减少2量子比特。前四个子线路中的每一个均可包含两个量子卷积核uc、两个量子池化核up和一个量子模糊卷积核ub，并具有相应的量子比特数目，每个量子核都对应一个酉矩阵，以形成量子判别线路120，其中，量子观测算符122表示约化密度矩阵操作，即将密度矩阵中的2个量子比特的信息丢弃，以达到量子网络里的下采样。量子判别线路120的最后一个子线路可包含一个uc、一个up、一个量子稠密核u
dense
和一个量子比特观测。该线路的输出将是量子判别线路120最终的判断结果。
34.量子卷积核，量子池化核，量子稠密核和量子模糊卷积核中的至少一者可包含两个子模块，一个是由任意旋转门组成的旋转模块，另一个是由受控非(cnot)门组成的纠缠模块。纠缠可使量子线路包含比较全面的输入数据的信息。任意旋转门可由3个分别绕着y轴、z轴、y轴的旋转操作组合而来，可调参数是旋转的角度。
35.图2为根据本技术一些实施例的量子卷积核uc的示意图。
36.量子卷积核uc可对量子态数据进行卷积操作，多比特量子卷积核可由2比特量子卷积核进行组装，以对输入数据进行特征提取。
37.如图2所示，rx、ry、rz各自代表泡利旋转门对应的x旋转门、y旋转门、z旋转门，θ代表旋转角，σ
x
，σy，σz分别为泡利x门，泡利y门和泡利z门；张量积运算符。
38.图3为根据本技术一些实施例的量子池化核up的示意图。
39.量子池化核对量子态数据进行池化操作，多比特量子池化核由2比特量子池化核组装，以对卷积所提取的信息进一步降维，减少计算量。
40.图4为根据本技术一些实施例的量子稠密核u
dense
的示意图。
41.量子稠密核作为全连接量子网络层对量子态数据进行操作。
42.图5为根据本技术一些实施例的量子模糊卷积核ub的示意图。
43.量子模糊卷积核对量子态数据进行模糊卷积操作，以实现提取特征，降低噪声和节省计算资源的作用。
44.本技术的一些实施例还提供一种用于渐进训练的模型，其包括生成器，以及上述量子判别线路。其中生成器可为经典网络模型中的结构，也可为量子线路。
45.图6为根据本技术一些实施例的用于渐进训练的模型示意图。
46.如图6所示，用于渐进训练的模型可包括生成器110以及量子判别线路120。
47.如图6所示，量子判别线路120可对训练集中的数据11和生成器110的输出进行判别，根据判别结果使用损失函数对量子判别线路120或生成器110进行优化。其中用于渐进
训练模型的生成器110可通过使用量子判别线路120进行优化以生成待预测的数据。
48.量子判别线路可包含参数化的泡利旋转门作为神经网络的可学习参数，通过受控门实现量子态纠缠，通过约化密度矩阵操作进行下采样，再通过测量得到判别分数，用于计算损失函数，进而可优化生成器和量子判别线路中的参数。其中参数化量子线路部分可采用量子卷积核，量子池化核，量子稠密核和量子模糊卷积核，按一定规律摆放(如模拟经典神经网络的摆放位置)来实现。
49.本技术采用如下两种损失函数对经典模型和上述用于渐进训练的模型进行优化和对比。
50.例如针对用于渐进训练的模型，采用非饱和的logistic损失计算损失函数：
51.lossg＝log(e-d(g(z))
+1),
ꢀꢀꢀꢀꢀꢀꢀ
(1)
52.lossd＝log(e
d(g(z))
+1)+log(e-d(x)
+1).
ꢀꢀꢀꢀꢀꢀꢀ
(2)
53.其中，g代表生成器，生成器输出棘突蛋白序列，输入z是隐码(或潜码)，可随机生成；d代表量子判别线路，x是真实数据。作为对比，可针对经典模型，添加惩罚项：
[0054][0055]
其中，取γ1＝10andγ2＝0。
[0056]
此外，也可采用relativistic-hinge损失函数进行计算：
[0057]
lossg＝e(relu(1+diff
rf
))+e(relu(1-diff
fr
)),
ꢀꢀꢀꢀ
(4)
[0058]
lossd＝e(relu(1-diff
rf
))+e(relu(1+diff
fr
)),
ꢀꢀꢀ
(5)
[0059]
其中，e代表求期望值，上述部分参数的计算公式如下：
[0060]
diff
rf
＝d(x)-e(d(g(z))),
ꢀꢀꢀꢀ
(6)
[0061]
diff
fr
＝d(g(z))-e(d(x)),
ꢀꢀꢀꢀ
(7)
[0062][0063]
基于训练的模型是人工智能领域的研究热点，可被应用在多种应用场景，如高清图像生成，风格图像生成等，然而这些模型的训练运行都需要消耗大量的计算资源。现有的模型训练运行的计算资源主要由电子集成电路制造的芯片提供，而随着电子遂穿效应对制程接近纳米极限后的制约，算力很难再持续提升。量子计算芯片是对电子芯片计算方式的补充，然而经典的模型训练在量子芯片上的运行无法按照其在电子芯片上的方式进行处理。
[0064]
本技术提出的用于渐进训练的模型可适用于多种应用场景，如生物医药、图像视频处理、材料、神经科学等领域。由于采用了量子-经典混合/全量子的数据处理方法，相比经典的方法均具有更广泛的应用场景。例如，本技术提出的用于渐进训练的模型可用于预测病毒变异结构。
[0065]
新冠病毒产生了具有更强传染性和致病性的变异毒株比如delta。根据现存的大量sars-cov-2突变rna序列数据，我们有机会提前预测新冠病毒流行株的变异结构(特别是棘突蛋白)，从而为早期预防和治疗提供可能，为控制疫情贡献力量。
[0066]
虽然传统的训练模型具有的风格迁移能力适用于covid-19变种结构生成，但是传统的训练模型中的生成器和判别器运算具有高度并行性并消耗大量计算资源。本技术提出
的量子判别线路，可运用量子-经典混合方式来处理covid-19变种结构生成问题，从而使得量子计算和经典计算能够协同工作用于covid-19变种结构生成的用于渐进训练的模型。
[0067]
例如，可使用上述量子判别线路用于通过生成器生成的covid-19毒株的棘突蛋白变异结构sg和covid-19毒株的棘突蛋白量子态sq进行判别，从而预测covid-19毒株的变异结构。
[0068]
首先需要将经典rna序列中的棘突蛋白部分数据编码为量子态。例如，可把长度为n的atcg格式棘突蛋白序列数据s与原始新冠相应位点对比，将突变的位点记为1，不变的位点记为0，得到长度为n的序列s1，这里，也可采用其它编码方式，之后可对棘突蛋白突变序列s1进行归一化操作(如l2归一化)得到新序列s2，将新棘突蛋白突变序列s2与它的共轭转置相乘，得到n
×
n的量子态密度矩阵sq以用于后续的量子计算。
[0069]
图7为根据本技术一些实施例的棘突蛋白序列的部分数据在excel中的表达形式。
[0070]
如图7所示，其中a列代表一些新冠病毒变种的命名编号，b列代表病毒rna序列，c列是病毒rna序列中的棘突蛋白序列，d列是01编码后的棘突蛋白序列，f是 1024位01编码后的部分棘突蛋白序列即s1。
[0071]
将图7中的棘突蛋白数据集转化为量子态密度矩阵，由于编码时用0或1表示相关信息，由此而得到的量子态密度矩阵将是一个稀疏矩阵，只有在对角线上可显示棘突蛋白突变序列，将经转化后得到的量子态密度矩阵使用本技术用于渐进训练的模型进行模拟计算，以及与经典模型的计算结果作对比，可得到图8和9中的计算结果。其中经典模型与本技术用于渐进训练的模型具有相同的生成器，但使用不同的判别线路，且经典模型不需要进行量子编码。
[0072]
图8和9为根据本技术一些实施例的在经典计算机上进行模拟的经典模型和本技术用于渐进训练的模型优化的对比结果。
[0073]
如图8所示，经典模型的生成器和判别线路的损失在整个过程中交替振荡，没有收敛。相比之下，本技术的用于渐进训练的模型中的生成器和判别线路的损失先剧烈振荡，然后在1000步左右收敛，之后保持轻微振荡。图9也展示了类似的情况，并且，我们可以在1500步后观察到更明显的收敛。这些结果证实了基于本技术用于渐进训练的模型的量子神经网络的巨大潜力以及混合量子经典模型可能产生的量子优势。
[0074]
应理解，虽然该实施例中的训练集为基因序列，但是这仅只是用于说明本技术提供的量子判别线路及用于渐进训练的模型的示范性实施例，而不应理解为对本技术所保护范围的限制。根据本技术的另一些实施例，其它类似数据的应用也可使用本技术提出的量子判别线路及用于渐进训练的模型。例如应用于图像视频的处理与分析。
[0075]
本技术的量子判别线路及用于渐进训练的模型使得需要优化的参数量大大减少，用到的存储介质，即量子比特数目也大大减少，从而使得基于量子计算的数据处理的方法更便捷、准确。
[0076]
本技术的技术内容及技术特点已揭示如上，然而熟悉本领域的技术人员仍可能基于本技术的教示及揭示而作种种不背离本技术精神的替换及修饰。因此，本技术的保护范围应不限于实施例所揭示的内容，而应包括各种不背离本技术的替换及修饰，并为本专利申请权利要求书所涵盖。