一种基于法向滤波的四边形网格生成方法

1.本发明属于计算机图形学领域，涉及一种基于法向滤波的四边形网格生成方法。


背景技术：

2.多边形网格是几何建模、计算机图形学、机械工程、仿真、建筑等领域的重要表示。这种表示是基于分解的思想：一个复杂的对象用简单的多边形单元的集合来表示。三角形和四边形是用于表达模型表面的最常见的单元。虽然三角形网格在计算机图形学中更为常见，大多数几何处理研究都集中在三角形网格上，但四边形网格(即完全由四边形组成的网格)在诸多应用中有着其独特的优势：
3.(1)在多边形建模中，大多数几何体具有两个主方向，通常与主曲率方向或局部锐利特征相关联，四边形可以用一组邻边来与几何体的主方向对齐，从而可以更好地捕获模型的几何特征。
4.(2)在高阶曲面建模中，b样条曲面和catmull-clark细分曲面，皆是张量积形式表示的四边形网格，可知四边形网格作为基网格可以非常有效的拟合b样条曲面或控制细分曲面。同时，四边形网格更符合当今工业标准。
5.(3)在纹理映射中，四边形网格的四边形单元近似于矩形，矩形纹理能够非常自然、低扭曲地映射到四边形网格表面。
6.(4)在有限元模拟仿真中，四边形网格在数值分析方面具有更好的性质，如计算精度更高、元素数量更少以及收敛速度更快等。在等距几何分析方面，由于四边形网格具有其网格边可与主曲率方向对齐的性质，其张量积函数更容易控制，而且具有更好的逼近能力。
7.(5)在压缩中，将一个高分辨率的形状存储为一个粗糙的四边形网格，并根据四边形网格上相关压缩位移的细节，可以大大减少存储空间以及传输时间。
8.故而，四边形网格比三角形网格更适用于以上许多任务，多年来在cad和仿真等领域中得到广泛的应用。但在实际应用中，为了生成高质量的四边形网格，就需要生成的网格中的四边形单元应相对来说比较平坦和接近矩形，并且应进行合理的安排，以遵循规定的方向，或形成适当的补丁，或两者兼而有之。提高四边形网格生成的自动化程度和精确度，到快速、鲁棒地设计出符合特定要求的理想全局结构，是四边形网格生成方法的研究目的。同时，四边形网格的优势普遍是基于具有良好性质的高质量四边形网格而存在的。因此，如何高质量、高效率、自动化地获取几何模型的四边形网格表示，为科学界和工业界持续关注，具有理论意义和实际意义。
9.近年来许多国内外专家学者针对四边形网格生成进行了深入研究，目前已经有很多算法，主要包含转换法、基于面片法、基于参数化法、场引导法这几大类方法，但是这些方法生成的四边形网格质量普遍并不高，总是会出现奇异点的数目较多、放置的位置不满足条件，生成的网格丢失部分信息，速度与质量相冲突等多种问题。


技术实现要素：

10.有鉴于此，本发明的目的在于提供一种基于法向滤波的四边形网格生成方法，能够在保留更多源模型信息的情况下，消除掉较多的奇异点，同时降低计算复杂度的方法，进行更快速有效的四边形网格生成。另外，本发明方法运行速度快，输入三角形网格后能够快速地给出四边形网格结果，效率较高，鲁棒性强，不仅适应于不同存储格式的三角形网格模型，也可以对点云等3d模型进行有效地四边形网格生成。
11.为达到上述目的，本发明提供如下技术方案：
12.一种基于法向滤波的四边形网格生成方法，该方法包括以下步骤：
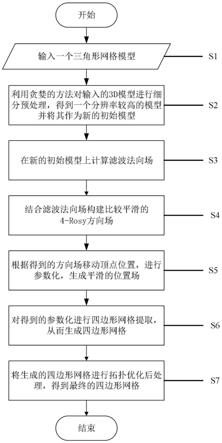
13.s1：输入一个三角形网格模型，支持.obj、.ply、.aln格式；
14.s2：利用贪婪的方法对输入的3d模型进行细分预处理，得到一个分辨率较高的模型并将其作为新的初始模型；
15.s3：在新的初始模型上计算滤波法向场，并归一化；
16.s4：结合滤波法向场构建比较平滑的4-rosy方向场；
17.s5：根据得到的方向场移动顶点位置，进行参数化，生成平滑的位置场；
18.s6：对得到的参数化进行四边形网格提取，从而生成四边形网格；
19.s7：将生成的四边形网格进行拓扑优化后处理，得到最终的四边形网格。
20.可选的，所述s2中，使用局部目标边长代替全局不变的目标边长实现局部自适应的网格细分：
[0021][0022]
local(e)＝min{l(k1)，l(k2)}
[0023]
其中，local_edge_length、k
min
、k
local
、target_edge_length分别表示顶点的局部目标边长、最小曲率、高斯曲率以及全局目标边长；并且对于网格上的每条边e，取其两个端点k1、k2对应的局部边长的最小值作为其对应的局部目标边长。
[0024]
可选的，所述s2中，使用贪婪的方法对输入的3d模型进行细分预处理，即将某些比较长的边分裂，使其都小于等于对应的局部目标边长。
[0025]
可选的，所述s3中，根据平均相邻面的角度加权方法为模型上的每个顶点v计算一个单位法向
[0026][0027][0028]
其中，为面fj的法向，n(v)是顶点v的一环邻域面集合，θj是邻域面fj与顶点v形成的夹角。
[0029]
可选的，所述s3中，将法向场与适当大小的高斯核σ卷积，以获得滤波法向场其中密集间隔的特征被合并；即对于每个顶点v，其滤波法向计算如下：
[0030]
[0031]
with
[0032][0033]
其中，dist(v-v')是3d模型m上点v和点v
′
之间的测地距离；是顶点v直到某个测地距离为2σ的邻域；av′
是顶点v
′
的局部邻域面积；σ一般为四边形目标尺寸s的1/2倍；法向进行归一化。
[0034]
可选的，所述s4具体包括如下步骤：
[0035]
s41：计算每个顶点的主曲率方向并归一化，将其作为初始方向场；
[0036]
s42：利用extrinsic smooth方法，构建平滑的方向场
[0037][0038]
with
[0039][0040][0041]
其中，n(i)表示顶点i的一环邻域顶点集合，是与每个顶点i∈v相关联的单位代表方向是围绕单位法向的旋转矩阵；该目标函数利用高斯塞尔迭代方法进行求解。
[0042]
可选的，所述s5中，利用extrinsic smooth方法，构建平滑的位置场：
[0043][0044]
with
[0045][0046][0047]
其中，pi为顶点i的代表位置，是与每个顶点i∈v相关联的单位代表方向n(i)表示顶点i的一环邻域顶点集合，s为四边形目标尺寸，其中集合q
ij
和q
ji
只包含产生靠近q
ij
位置的位移；该目标函数利用高斯塞尔迭代方法进行求解。
[0048]
可选的，所述s6中，包括图结构提取和四边形面提取两个部分；
[0049]
其中，图结构提取具体包括：全局参数化的网格和场，边长预估，边的识别，边的折叠，边的修正，确定顶点，移除不需要的边，边方向对齐；
[0050]
四边形面提取具体包括：四边形面提取，四边形面重排序。
[0051]
可选的，所述s7中，拓扑优化的原则为：对于度为3或者度为5的不规则节点，进行合并操作减少其数量；对于度为2或者度大于6的不规则节点，进行删除，最终的网格中不含有这两类不规则节点；
[0052]
对于细分非规则面，利用catmull-clark方法；即每个面计算生成一个新的顶点，每条边计算生成一个新的顶点，同时每个原始顶点更新位置；对于新增加的顶点位置以及
原始顶点位置更新规则如下：
[0053]
(1)网格内部f-顶点位置：设四边形的四个顶点为v0、v1、v2、v3，则新增加的顶点位置为v＝1/4*(v0+v1+v2+v3)；
[0054]
(2)网格内部v-顶点位置：设内部顶点v0的相邻点为v1,v2,
…
,v
2n
，则该顶点更新后位置为其中α、β、γ分别为α＝1-β-γ；
[0055]
(3)网格边界v-顶点位置：设边界顶点v0的两个相邻点为v1、v2，则该顶点更新后位置为v＝3/4*v0+1/8*(v1+v2)；
[0056]
(4)网格内部e-顶点位置：设内部边的两个端点为v0、v1，与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5，则新增加的顶点位置为加的顶点位置为
[0057]
(5)网格边界e-顶点位置：设边界边的两个端点为v0、v1，则新增加的顶点位置为v＝1/2*(v0+v1)。
[0058]
本发明的有益效果在于：本发明提供的基于法向滤波的四边形网格生成方法使用贪婪的方法对输入网格进行自适应网格划分预处理，并将其预处理的结果作为后面的初始模型。同时使用高斯滤波来滤波法向，使方向场奇异点更加分散，在一定程度上使奇异点数目减少。而使用主曲率方向初始化方向场，也在生成的四边形网格质量上有所提升。本发明所述方法计算简单，采用并行计算加快运行速度，鲁棒性强，生成的四边形网格效果较好，针对不同存储格式的3d模型有者很强的适应性。
[0059]
本发明的其他优点、目标和特征在某种程度上将在随后的说明书中进行阐述，并且在某种程度上，基于对下文的考察研究对本领域技术人员而言将是显而易见的，或者可以从本发明的实践中得到教导。本发明的目标和其他优点可以通过下面的说明书来实现和获得。
附图说明
[0060]
为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作优选的详细描述，其中：
[0061]
图1为本发明方法的流程图；
[0062]
图2为本实施例输入一个三角形网格及细分预处理结果；
[0063]
图3为本实施例生成的方向场结果；
[0064]
图4为本实施例生成的位置场结果；
[0065]
图5为本实施例生成的四边形网格结果图。
具体实施方式
[0066]
以下通过特定的具体实例说明本发明的实施方式，本领域技术人员可由本说明书所揭露的内容轻易地了解本发明的其他优点与功效。本发明还可以通过另外不同的具体实施方式加以实施或应用，本说明书中的各项细节也可以基于不同观点与应用，在没有背离本发明的精神下进行各种修饰或改变。需要说明的是，以下实施例中所提供的图示仅以示
意方式说明本发明的基本构想，在不冲突的情况下，以下实施例及实施例中的特征可以相互组合。
[0067]
其中，附图仅用于示例性说明，表示的仅是示意图，而非实物图，不能理解为对本发明的限制；为了更好地说明本发明的实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；对本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。
[0068]
本发明实施例的附图中相同或相似的标号对应相同或相似的部件；在本发明的描述中，需要理解的是，若有术语“上”、“下”、“左”、“右”、“前”、“后”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此附图中描述位置关系的用语仅用于示例性说明，不能理解为对本发明的限制，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。
[0069]
请参阅图1～图5，本发明提供的基于法向滤波的四边形网格生成方法，包括以下步骤：
[0070]
s1：输入一个三角形网格模型，主要支持.obj、.ply、.aln格式；
[0071]
s2：利用贪婪的方法对输入的3d模型进行细分预处理，得到一个分辨率较高的模型并将其作为新的初始模型；
[0072]
s3：在新的初始模型上计算滤波法向场，并归一化；
[0073]
s4：结合滤波法向场构建比较平滑的4-rosy方向场；
[0074]
s5：根据得到的方向场移动顶点位置，进行参数化，生成平滑的位置场；
[0075]
s6：对得到的参数化进行四边形网格提取，从而生成四边形网格；
[0076]
s7：将生成的四边形网格进行拓扑优化后处理，得到最终的四边形网格。
[0077]
在本实施例中，初始输入三角形网格为斯坦福3d扫描存储库获得，其包括不同形状以及不同存储格式的3d模型，默认为.obj存储格式。使用局部目标边长代替全局不变的目标边长实现局部自适应的网格细分：
[0078][0079]
local(e)＝min{l(k1)，l(k2)}
[0080]
其中，local_edge_length、k
min
、k
local
、target_edge_length分别表示顶点的局部目标边长、最小曲率、高斯曲率以及全局目标边长。并且对于网格上的每条边e，取其两个端点k1、k2对应的局部边长的最小值作为其对应的局部目标边长。
[0081]
图2为使用贪婪的方法对输入的3d模型进行细分预处理，即将某些比较长的边分裂，使其都小于等于利用上述计算而来的局部目标边长的结果图像，并将其作为后续步骤的初始网格模型。
[0082]
在本实施例中，根据平均相邻面的角度加权方法为模型上的每个顶点v计算一个单位法向
[0083]
[0084][0085]
其中，为面fj的法向，n(v)是顶点v的一环邻域面集合，θj是邻域面fj与顶点v形成的夹角。
[0086]
将上一步计算得到的单位法向场与适当大小的高斯核σ卷积，以获得滤波法向场其中密集间隔的特征被合并。即对于每个顶点v，其滤波法向计算如下：
[0087][0088]
with
[0089][0090]
其中，dist(v-v')是3d模型m上点v和点v
′
之间的测地距离。是顶点v直到某个测地距离为2σ的邻域。av′
是顶点v
′
的局部邻域面积。σ一般为四边形目标尺寸s的1/2倍。
[0091]
将滤波法向进行归一化处理，即每个顶点法向模长都为1。
[0092]
在本实施例中，首先计算每个顶点的主曲率方向并归一化，将其作为初始方向场。然后利用extrinsic smooth方法，构建平滑的方向场：
[0093][0094]
with
[0095][0096][0097]
其中，n(i)表示顶点i的一环邻域顶点集合，是与每个顶点i∈v相关联的单位代表方向是围绕单位法向的旋转矩阵。如图3所示，为利用高斯塞尔迭代方法对该目标函数进行求解的结果。
[0098]
根据得到的方向场移动顶点位置，进行参数化，利用extrinsic smooth方法，生成平滑的位置场：
[0099][0100]
with
[0101][0102][0103]
其中，pi为顶点i的代表位置，是与每个顶点i∈v相关联的单位代表方向n(i)表示顶点i的一环邻域顶点集合，s为四边形目标尺寸，其中集合q
ij
和q
ji
只包含产生靠
近q
ij
位置的位移。如图4所示，为利用高斯塞尔迭代方法对该目标函数进行求解的结果。
[0104]
对得到的参数化进行四边形网格提取，主要包括图结构提取和四边形面提取两个部分。
[0105]
其中，图结构提取具体包括：全局参数化的网格和场，边长预估，边的识别，边的折叠，边的修正，确定顶点，移除不需要的边，边方向对齐。
[0106]
四边形面提取具体包括：四边形面提取，四边形面重排序。
[0107]
最后，将上述实施方法生成的四边形网格进行拓扑优化，即可得到最终的四边形网格。拓扑优化的原则为：对于度为3或者度为5的不规则节点，应进行合并操作尽量减少其数量；而对于度为2或者度大于6的不规则节点，则应该进行删除，最终的网格中应不含有这两类不规则节点。
[0108]
对于细分非规则面，利用catmull-clark方法。即每个面计算生成一个新的顶点，每条边计算生成一个新的顶点，同时每个原始顶点更新位置。对于新增加的顶点位置以及原始顶点位置更新规则如下：
[0109]
(1)网格内部f-顶点位置：设四边形的四个顶点为v0、v1、v2、v3，则新增加的顶点位置为v＝1/4*(v0+v1+v2+v3)。
[0110]
(2)网格内部v-顶点位置：设内部顶点v0的相邻点为v1,v2,
…
,v
2n
，则该顶点更新后位置为其中α、β、γ分别为α＝1-β-γ。
[0111]
(3)网格边界v-顶点位置：设边界顶点v0的两个相邻点为v1、v2，则该顶点更新后位置为v＝3/4*v0+1/8*(v1+v2)。
[0112]
(4)网格内部e-顶点位置：设内部边的两个端点为v0、v1，与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5，则新增加的顶点位置为，则新增加的顶点位置为
[0113]
(5)网格边界e-顶点位置：设边界边的两个端点为v0、v1，则新增加的顶点位置为v＝1/2*(v0+v1)。
[0114]
上述四边形网格生成方法是基于法向滤波的，利用高斯法向滤波以及主曲率方向初始化，保证了奇异点的分散以及数量减少、特征信息的保留。同时，利用着色算法，将相互有影响的顶点作为同一组，无影响的组之间进行并行运算，加快了整体算法的运行速度。图5是本发明方法对含有尖锐特征模型的四边形网格生成结果，可以看出生成的四边形网格很好的保留了尖锐特征，不规则顶点较少。本发明方法运行速度快，效率较高，鲁棒性强，不仅适用于.obj、.ply等常见存储格式模型，也可以对点云等模型进行有效地四边形网格生成。
[0115]
最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。