基于深度3D卷积稀疏编码的多光谱图像去噪算法

基于深度3d卷积稀疏编码的多光谱图像去噪算法
技术领域
1.本发明涉及图像处理技术领域，具体的说是基于深度3d卷积稀疏编码的多光谱图像去噪算法。


背景技术：

2.多光谱图像是一种包含多个波段的图像，它由特定的成像技术把入射的全波段或宽波段的光信号分成若干个窄波段的光束，然后通过同多个波段传感器进行成像，从而获得多光谱波段的图像。与灰度图像和普通的彩色图像相比，多光谱图像波段数较多，包含有更加丰富的光谱信息，被广泛应用于多场景，比如农作物检测、医疗肿瘤定位、工业检测等。然而，多光谱图像成像过程中，常常会受设备、外部环境噪声等干扰，导致采集到的图像包含噪声，从而影响后续研究的准确性，比如土壤成分检测错误、肿瘤定位不准确、部件检验异常等。因此，多光谱图像去噪具有重要的实际应用价值。
3.图像去噪的任务是从噪声图像中重构出干净的图像。现有的图像去噪方法主要分为基于模型的方法和基于深度学习的方法。基于模型的方法的主要思想是通过引入不同的先验信息将图像去噪问题转变为优化求解问题。常用的先验信息有全变分约束、稀疏先验约束等。基于模型的方法有着较强的可解释性，但是其性能很大程度上依赖人工的参数设计，灵活性较差。近些年，随着深度学习的兴起，基于深度神经网络的去噪模型得到了广泛关注，比如dncnn、cnlnet等，这些网络的核心思想是通过端到端的策略训练神经网络，将噪声图像映射到干净图像。与基于模型的方法相比，基于深度学习的图像去噪算法取得了很大的性能提升。但现有深度去噪网络主要是人工构造，可解释性较差。
4.为了提高深度神经网络的可解释性，研究者们提出了基于深度展开的深度神经网络，起源于一种称为可学习的迭代收缩软阈值算法(lista)。lista将待针对稀疏模型求解的软阈值算法的迭代解展开成深度网络，其中深度网络中的每一层都对应每次迭代。基于lista思想，深度展开也被应用于图像去噪，可解比如cscnet、groupsc等。现有的实验结果表明，在这些可解释性网络与经典的深度去噪网络有相仿的性能的同时，它们还有着更少的参数与较强的可解释性。但这些可解释性的网络没有很好地刻画图像本身谱间特征，因此，本发明设计了一种基于深度3d卷积稀疏编码模型的多光谱图像去噪网络。


技术实现要素：

5.为了解决上述问题，本发明提供了一种能够提高深度神经网络的可解释性的基于深度3d卷积稀疏编码的多光谱图像去噪算法。
6.为了达到上述目的，本发明是通过以下技术方案来实现的：
7.本发明是基于深度3d卷积稀疏编码的多光谱图像去噪算法，包括如下步骤：
8.步骤1，根据多光谱图像的谱间信息，将卷积稀疏编码模型拓展成3d形式，搭建3d-csc数学模型；
9.步骤2，采用迭代收缩软阈值算法对搭建的3d-csc模型进行迭代求解；
10.步骤3，搭建深度网络：根据深度展开的思想，将步骤2中的3d-csc的迭代解形式展开成对应的深度网络3d-cscnet；
11.步骤4，构造数据集后训练网络；
12.步骤5，测试网络的性能。
13.本发明的进一步改进在于：步骤1的具体操作为：
14.步骤1.1，卷积稀疏编码模型将x表示成m个卷积特征的线性组合形式，根据多光谱图像的空间结构，将其拓展到3d形式则有：
[0015][0016]
其中x代表干净的多光谱图像，表示m个大小为h
×h×
h的滤波器，*表示三维卷积，表示第i个滤波器di对应的卷积特征；
[0017]
步骤1.2，卷积稀疏编码假设是稀疏的，即含有少量的非零元素，通过下面的优化问题求得：
[0018][0019]
其中||
·
||1代表l1范数，λ是正则化参数。
[0020]
本发明的进一步改进在于：步骤2中迭代求解的具体过程为：公式(2)的迭代更新公式为：
[0021][0022]
其中a是对应的稀疏编码，上标t表示第t(t＝0，1，2，...，k-1)次迭代值，t为转置符号，l是拉普拉斯常数，λ
t
为第t次迭代对应的正则化参数，是软阈值操作子，定义为：
[0023][0024]
本发明的进一步改进在于：步骤3具体步骤为：通过引入变量b＝d将公式(3)转化为：
[0025][0026]
将公式(5)展开成深度神经网络，其中神经网络的第t层对应公式的第t次迭代，在网络中起激活函数的作用，c和b则通过卷积实现并在网络训练过程中不断学习优化。
[0027]
本发明的进一步改进在于：步骤4具体步骤如下：
[0028]
步骤4.1，构造数据集；
[0029]
步骤4.2，初始化参数；
[0030]
步骤4.3，训练3d-cscnet；
[0031]
步骤4.4，重构输出图像。
[0032]
本发明的有益效果是：本发明运用了3d卷积，考虑了多光谱图像的谱间特征，将原始的卷积稀疏编码拓展到3d形式，搭建对应的3d去噪深度网络，使得本发明所搭建的网络
具有一定可解释性的同时，在处理多光谱图像问题上也取得了较好的去噪效果。
附图说明
[0033]
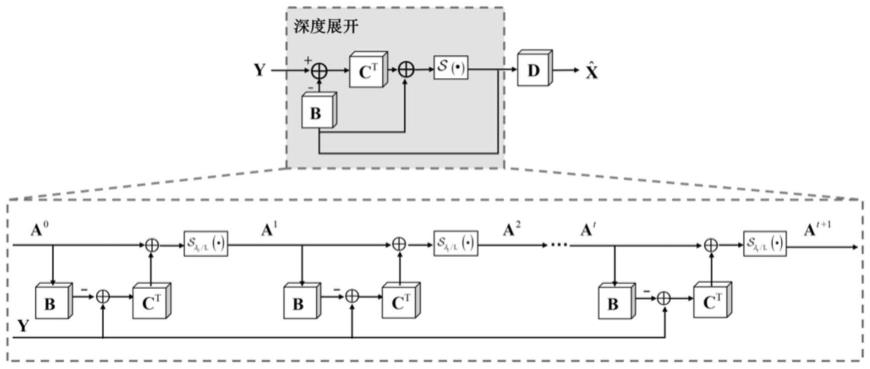
图1为3d-cscnet的网络结构图。
具体实施方式
[0034]
为了更清楚地说明本发明的技术方案，下面结合附图对本发明的技术方案做进一步的详细说明：
[0035]
本发明是一种基于深度3d卷积稀疏编码的多光谱图像去噪算法，考虑到多光谱图像具有一定的空间结构，本发明提出一种基于3d卷积字典的卷积稀疏编码模型，并利用交替迭代优化算法对其进行求解。然后，利用深度展开策略将迭代优化解转化成3d-cscnet，对应的网络图如图1所示。
[0036]
常见的噪声图像可以表示为：
[0037]
y＝x+n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)其中，代表干净的多光谱图像，为噪声，本发明仅考虑高斯噪声，代表噪声图像，m
×
n代表图像的空间尺寸，c代表图像的波段数。图像去噪就是如何从y中恢复出x。本发明的去噪方法具体包括如下步骤：
[0038]
步骤1，根据多光谱图像的谱间信息，将卷积稀疏编码模型拓展成3d形式，搭建3d-csc数学模型；
[0039]
步骤2，采用迭代收缩软阈值算法(ista)对搭建的3d-csc模型进行迭代求解；
[0040]
步骤3，搭建深度网络：根据深度展开的思想，将步骤2中的3d-csc的迭代解形式展开成对应的深度网络；
[0041]
步骤4，构造数据集后训练网络；
[0042]
步骤5，测试网络的性能。
[0043]
步骤1中，卷积稀疏编码模型将x表示成m个卷积特征的线性组合形式，根据多光谱图像的空间结构，将其拓展到3d形式则有：
[0044][0045]
其中表示m个大小为h
×h×
h的滤波器，*表示三维卷积，表示第i个滤波器di对应的卷积特征。卷积稀疏编码假设是稀疏的，即含有少量的非零元素，可以通过下面的优化问题求得：
[0046][0047]
其中||
·
||1代表l1范数，λ是正则化参数。
[0048]
步骤2中应用ista算法迭代求解步骤1中原问题，得到每一层的稀疏表示向量；
[0049]
求解的过程为：
[0050]
公式(3)ista的迭代更新公式为：
[0051]
[0052]
其中a是对应的稀疏编码，t表示第t(t＝0，1，2，...，k-1)次迭代值，是软阈值操作子，t为转置符号，l是拉普拉斯常数，λ
t
为第t次迭代对应的正则化参数，定义为：
[0053][0054]
步骤3中，采用深度展开策略，将3d-csc模型展开成3d-cscnet，具体方法为：采用深度展开思想将公式(4)展开成深度神经网络。首先，通过引入变量b＝d将公式(4)转化为：
[0055][0056]
然后，将公式(6)展开成深度神经网络，其中神经网络的第t层对应公式的第t次迭代，即，每一次迭代解对应神经网络中的每一层，在网络中起激活函数的作用，c和b则通过卷积实现并在网络训练过程中不断学习优化。
[0057]
步骤4具体包括：构造数据集、初始化参数、训练3d-cscnet和重构输出图像。
[0058]
构造数据集：本发明的网络训练采用数据集cave，一共有32个场景，每个场景有31张大小为512
×
512的灰度图像，对应这个场景的31个波段。因此，本发明将这31张灰度图像按顺序合成为一个三维张量，大小为512
×
512
×
31。在读入数据前，本发明将这些三维张量按照32
×
32的大小进行切割处理，切割间隔的步长为31个像素值，并将这些合成后的张量保存成mat文件以便后续导入数据，最终将这些切割好的数据在归一化处理后按6：4的比例将其划分成训练集和测试集，数据经过归一化处理后的灰度范围为[0，1]。
[0059]
初始化参数：输入一幅多光谱图像y，随机初始化3d字典d，正则化参数λ；
[0060]
训练3d-cscnet：本发明通过手动添加高斯噪声来模拟噪声图像。整个3d-cscnet的网络参数有θ＝{c，b，d，λ}，这些参数可以通过网络以一种端到端监督学习的形式训练得到。本发明采用的损失函数是均方误差(mse)损失函数，定义为
[0061][0062]
其中，m是训练样本的数量，f
θ
代表参数为θ的3d-cscnet，yj代表第j个训练样本，f
θ
(yj)是3d-cscnet的估计值。本发明在pytorch上实现3d-cscnet，在rtx2070super gpu上进行训练和测试，训练一次抓取的样本数量(batch size)和训练轮数(epoch)设置为8和200，卷积核大小为7
×
7，并采用adam优化器。训练3d-cscnet时设定堆展开数k，在求解t(t＝0，1，2，...，k)层对应的稀疏编码时，应用式(6)，知道设定的迭代结束。
[0063]
重构输出图像：由最终的ak，根据重构去噪后的图像。
[0064]
步骤5测试模型的具体方法为：在σ＝{0.1，0.2，0.3}三个不同噪声等级下对网络性能进行评价，评价指标采用平均峰值信噪比(mean peak signal-to-noise ratio，mpsnr)。对比方法包括lrmr、lrtv、llrgtv和cscnet，实验结果见表1：
[0065]
表1在cave测试集上不同方法的mpsnr结果
[0066]
算法σ＝25σ＝50σ＝75lrmr33.4828.4425.00
lrtv36.2132.0329.41llrgtv34.4029.7126.82cscnet35.3632.5030.213d-cscnet37.4033.5325.69
[0067]
由表1可见，本发明的3d-cscnet有着较好的去噪性能。值得注意的是，与cscnet相比，3d-cscnet在cave这个数据集上，在σ取值为25和50常用噪声下，表现更加优异，这也证明了模型的有效性。