一种预应力锚固路基预应力损失分析方法

1.本发明属于土木工程技术领域，尤其涉及一种预应力锚固路基预应力损失分析方法。


背景技术：

2.预应力锚固/加固技术广泛应用于边坡、基坑及矿业等工程领域。作为预应力锚固技术的核心，预应力水平及其随时间的变化规律关乎锚固工程的成败。实际工程中，由于预应力损失过量而导致锚固工程失效的事故时有发生，由此引起的经济损失十分巨大。因此，针对具体的预应力锚固技术，研究其预应力损失规律对保障锚固工程的长期安全具有重大意义。
3.以往的研究中，大多集中于黏结型预应力锚固结构，该类结构由于锚杆与周围土体存在明显的黏结效应，可近似认为锚杆应变与周围岩土体应变相等，因此以往研究多针对黏结型预应力锚固结构且基于等应变的原理描述岩土体蠕变引起的预应力损失变化规律。然而，预应力路基中预应力筋由保护套管包裹，其与路基土不存在接触与摩擦关系，属于对穿全长无黏结预应力锚固结构，等应变假设不再适用。另外，关于对穿无黏结岩土体预应力锚固结构，通常将被加固岩土体沿锚索或锚杆轴向的变形简化为均匀分布，并分析其预应力损失特性；然而，预应力路基中，由预应力加固组件引起的附加应力存在显著的扩散效应，不同位置处路基土的变形大小不一，无法假设为均匀分布。
4.综上，有必要提出一种新型预应力锚固路基预应力损失分析方法。


技术实现要素：

5.本发明的主要目的在于提供一种预应力锚固路基预应力损失分析方法，该分析方法能够准确预测土体蠕变引起的预应力钢筋张拉力损失，进而能够指导后续预应力的补张拉，对保障锚固工程的长期安全具有重大意义。
6.为此，本发明提供的预应力锚固路基预应力损失分析方法，所述路基通过加固组件进行加固，所述加固组件包括设置在路基两侧的两块侧压板、锚固在两块侧压板之间的预应力钢筋以及套在预应力钢筋外的保护套管，该方法包括如下步骤：
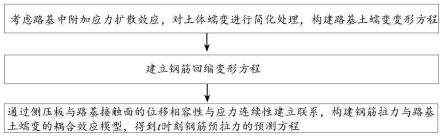
7.步骤一、考虑路基中附加应力扩散效应，对土体蠕变进行简化处理，采用单元土体的初始水平向附加应力和t时刻水平附加应力的均值计算路基土的蠕变应变，得到路基土蠕变变形方程；
8.步骤二、建立钢筋回缩变形方程；
9.步骤三、将钢筋、侧压板与路基接触面中心点后方土体视为多个相互独立的元件模型，通过侧压板与路基接触面的位移相容性与应力连续性建立联系，构建钢筋张拉力与路基土蠕变的耦合效应模型，得到t时刻钢筋张拉力f
pt
的预测方程：
[0010][0011][0012]
其中：t为时间，f
p0
为钢筋的初始张拉力，h为路基两侧侧压板与路基接触面中心点的水平距离，b和l分别为侧压板底面沿线路纵向和路基坡面方向的长度，as为钢筋截面面积，es为钢筋的弹性模量，kh为侧压板与路基接触面中心点后方水平路径上任一点处的水平附加应力系数，em、ek分别为maxwell体、kelvin体的弹性常数，ηm、ηk分别为maxwell体、kelvin体的黏性常数，h为侧压板与路基接触面中心点后方水平路径上土体单元i距路基坡面的水平距离。
[0013]
具体的，路基土蠕变变形方程的表达式为：
[0014][0015]
其中：l
st
为路基土的蠕变变形量，q0、q
t
分别为侧压板与路基接触面处的初始水平均布荷载和t时刻水平均布荷载。
[0016]
具体的，将预应力钢筋采用虎克体模拟，则半幅路基模型下钢筋沿其轴向的回缩应变ε
pt
和回缩变形l
pt
具体表达式如下：
[0017][0018][0019]
具体的，步骤三具体包括如下步骤：
[0020]
将侧压板作用于路基坡面的预压应力简化为水平向矩形均布荷载q，则侧压板与路基接触面处的初始水平均布荷载q0和t时刻水平均布荷载q
t
可分别表示为：
[0021][0022][0023]
在不考虑锚具和侧压板变形的情况下，则任意t时刻钢筋的回缩变形l
pt
与路基土的蠕变变形l
st
满足如下关系：
[0024]
l
st
＝l
pt
[0025]
联立上述关系式，即可得到钢筋张拉力f
pt
的表达式。
[0026]
具体的，kh的表达式为：
[0027]
kh＝m
·
exp(n
·
(h/b)+c)
[0028]
式中：m、n、c为水平附加应力分布曲线拟合参数。
[0029]
与现有技术相比，本发明具有如下优点效果：本技术基于预应力钢筋回缩变形与路基土蠕变变形的相容性、路基两侧侧压板与路基土接触面处的应力连续性及路基内附加
应力的扩散效应而提出，考虑了附加应力在预应力路基内的扩散效应，计算原理清晰，对土体蠕变处理简便，得到的预测方程能够准确预测土体蠕变引起的预应力钢筋张拉力损失，进而能够指导后续预应力的补张拉，对保障锚固工程的长期安全具有重大意义。
附图说明
[0030]
为了更清楚地说明本发明实施例中的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0031]
图1是本发明实施例的流程图；
[0032]
图2是本发明实施例涉及的预应力锚固路基结构示意图；
[0033]
图3是本发明实施例涉及的半幅预应力路基过侧压力板中心线剖面示意图；
[0034]
图4为本发明实施例涉及的预应力锚固路基力学计算模型示意图；
[0035]
图5为本发明实施例涉及的水平附加应力计算示意图；
[0036]
图6为本发明实施例涉及的分块荷载pfbe及上、下角点示意图；
[0037]
图7为本发明实施例涉及的3种典型坡率下k
h-h/b关系曲线图；
[0038]
图8为本发明实施例涉及的耦合效应模型示意图。
具体实施方式
[0039]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0040]
在本发明的描述中，需要理解的是，术语“中心”、“纵向”、“横向”、“长度”、“宽度”、“厚度”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”、“顺时针”、“逆时针”、“轴向”、“径向”、“周向”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。
[0041]
此外，术语“第一”、“第二”仅用于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括一个或者更多个该特征。在本发明的描述中，“多个”的含义是两个或两个以上，除非另有明确具体的限定。
[0042]
参见图1，一种利用上述加固组件加固的预应力锚固路基预应力损失分析方法，包括如下步骤：
[0043]
步骤一、考虑路基中附加应力扩散效应，对土体蠕变进行简化处理，采用单元土体的初始水平向附加应力和t时刻水平附加应力的均值计算路基土的蠕变应变，得到路基土蠕变变形方程；
[0044]
图2所示为预应力锚固路基结构示意图，该路基通过加固组件进行加固，加固组件包括设置在路基两侧的两块侧压板、锚固在两块侧压板之间的预应力钢筋以及套在预应力
钢筋外的保护套管，预应力路基为对称结构，其中板-土接触面(侧压板与路基的接触面)设置了锯齿状防滑台阶(见图2)，且路基在钢筋张拉力吨位较小时(如10t)即可达到较好的加固效果，图3为半幅预应力路基过侧压板中心线的剖面示意图，其中f
p
为钢筋张拉力，h为侧压板与路基接触面中心点后方水平路径上土体单元i距路基坡面的水平距离，h为路基两侧侧压板与路基接触面中心点的水平距离，θ为路基坡角，b和l分别为侧压板底面沿线路纵向和路基坡面方向的长度。
[0045]
本发明在分析预应力路基附加应力扩散规律时，保留其三维空间问题的基本特征(如图3)，由于分析的侧重点为板-土接触面中心点(即特征点)后方水平路径(见图3)上的附加应力分布规律，为便于表述，其力学模型基于过侧压板中心线的路基剖面进行示意和说明；
[0046]
如图4所示，以侧压板底面中心为原点建立三维坐标系，其中x轴沿路基坡向，y轴沿线路纵向，z轴沿路基坡面法向，将侧压板作用于路基坡面的预压应力简化为水平向矩形均布荷载q，q可进一步分解为沿坡面法向的均布荷载qn和沿坡面切向的切向均布荷载q
t
。基于土力学中附加应力计算的分块角点法，以板-土接触面中心为共有角点将侧压板与路基接触面等分为4块(如图4)；则板-土接触面中心点后方水平路径上任一点处的水平向附加应力σh为：
[0047][0048]
σh＝qkh＝qk
h-peah
+qk
h-pfbe
+qk
h-pfcg
+qk
h-pgdh
ꢀꢀꢀ
(2)
[0049]
式中：kh为板-土接触面中心点p后方水平路径上任一点处的水平附加应力系数；下标peah、pfbe、pfcg、pgdh分别指代图4中相应的荷载分块。水平附加应力σh的具体推导过程如下：
[0050]
研究预应力在路基内水平向的扩散规律时，需转换土体单元i的应力计算方向。根据应力状态分析理论可知，土体单元i任一方向上的附加正应力可由图5中计算坐标系下的六个应力分量σ
x
、σy、σz、τ
xy
＝τ
yx
、τ
yz
＝τ
zy
和τ
zx
＝τ
xz
求得，故预应力路基内的水平附加应力σh可表示为：
[0051]
σh＝l2σ
x
+m2σy+n2σz+2mnτ
yz
+2nlτ
zx
+2lmτ
xy
ꢀꢀꢀ
(3)
[0052]
式中：σ
x
、σy和σz分别为土体单元i在水平均布荷载q作用下沿x向(路基坡向)、y向(线路纵向)和z向(坡面法向)的附加正应力；τ
xy
、τ
yz
和τ
xz
分别为土体单元i在水平均布荷载q作用下在面xy、yz和xz内的附加切应力；l，m和n为方向余弦，其中l＝cos(h，x)，m＝cos(h，y)，n＝cos(h，z)。
[0053]
路基内水平附加应力的分析图示如图5，根据图4建立的坐标系可知，水平方向与y向(线路纵向)垂直，即方向余弦m＝cos(h，y)＝0，故预应力路基内的水平附加应力σh可简化为：
[0054]
σh＝l2σ
x
+n2σz+2nlτ
xz
ꢀꢀꢀ
(4)
[0055]
可见，求解水平附加应力σh只需求出附加应力分量σ
x
、σz和τ
xz
。图3各分块荷载沿坡面法向的荷载分量qn和沿坡切向的切向荷载分量q
t
于分块荷载角点处引起的附加应力分量，可分别由弹性理论中的boussinesq公式和cerruti公式积分求得；
[0056]
如图6所示，以分块荷载pfbe为例推导，附加应力分量具体表达式如下：
[0057][0058][0059][0060][0061][0062][0063]
式中：σ
xn
、σ
zn
和τ
xzn
分别为法向均布荷载qn作用下土体单元i的x向(路基坡向)、z向(坡面法向)附加正应力及xz平面内的附加切应力；σ
xt
、σ
zt
和τ
xzt
分别为切向均布荷载q
t
作用下土体单元i的x向、z向附加正应力及xz平面内的附加切应力；ω表示分块荷载面积；μ为泊松比；x、y、z分别表示土体单元i的x坐标、y坐标和z坐标；r为土体单元i距离坐标原点的距离：
[0064]
r＝(x2+y2+z2)
1/2
。
[0065]
根据应力状态分析理论，可进一步求得分块荷载pfbe上、下角点(如图4和图6所示，其中靠近路肩位置的角点为上角点(如点b和e)，靠近路基坡脚位置角点为下角点(如点f和p))处的水平向附加应力σ
hu
和σ
hd
，具体表达式如下：
[0066]
σ
hu
＝qk
zu
＝(σ
xn
+σ
xt
)cos2θ+(σ
zn
+σ
zt
)sin2θ+(-τ
xzn
+τ
xzt
)sin2θ
ꢀꢀꢀ
(11)
[0067]
σ
hd
＝qk
zd
＝(σ
xn-σ
xt
)cos2θ+(σ
zn-σ
zt
)sin2θ+(τ
xzn
+τ
xzt
)sin2θ
ꢀꢀꢀ
(12)
[0068]
式中：k
zu
、k
zd
分别表示为分块荷载pfbe上、下角点处z向路径上任一点处的水平附加应力系数。
[0069]
进一步根据分块叠加原理和计算路径转换方法即可求得板-土接触面中心点后方水平路径各点处的水平向附加应力，将板-土接触面中心点后方水平附加应力系数kh随h/b的变化关系曲线采用指数函数拟合，具体表达式如下：
[0070]
kh＝m
·
exp(n
·
(h/b)+c)
ꢀꢀꢀ
(13)
[0071]
式中：m、n、c为水平附加应力分布曲线拟合参数，典型指数函数拟合效果见图7。本发明采用burgers模型描述路基土的蠕变行为，其蠕变方程具体表达式为：
[0072][0073]
ε＝σc (15)
[0074][0075]
式中：t为时间，σ、ε分别表示路基土所受蠕变应力及产生的蠕变应变；分别表示路基土蠕变应力和蠕变应变对时间的一阶导数；分别表示路基土蠕变应力和蠕
变应变对时间的二阶导数；em、ek分别为maxwell体、kelvin体的弹性常数，ηm、ηk分别为maxwell体、kelvin体的黏性常数，具体数值可通过室内蠕变试验及参数反演得到。
[0076]
以侧压板后方水平路径上某一土体单元i为研究对象(如图3)，令钢筋锁定后该单元土体的初始水平向附加应为σ
h0
；由于预应力的损失效应，土体的附加应力会随时间推移而减小，令t时刻单元土体的水平附加应力为σ
ht
；既有研究多采用恒定附加应力计算土体的蠕变应变，即ε
ht
＝σ
h0
c，然而，预应力路基内的附加应力与土体蠕变存在显著的耦合效应，单元土体i所受附加应力σh随时间是不断衰减的，若按初始附加应力σ
h0
计算土体蠕变变形，则计算结果偏大，即若按计算时刻(即t时刻)的附加应力σ
ht
考虑，则计算结果偏小，即实际路基土的蠕变应变应介于二者之间。因此，本发明采用单元土体的初始水平向附加应力σ
h0
和t时刻水平附加应力σ
ht
的均值计算路基土的蠕变应变具体表达式如下：
[0077][0078]
依据burgers模型中maxwell体的弹性常数em，则单元土体i在初始时刻的瞬时应变具体表达式为：
[0079][0080]
因此，单元土体i的后续蠕变应变ε
ht
为：
[0081][0082][0083]
伴随钢筋预应力的损失过程，单元土体i所受的附加应力实际处于不断减小的状态，直至钢筋与土体之间的变形协调与内力平衡过程达到稳定后，预应力方才保持不变，因此，应考虑卸载过程(即附加应力衰减)中的单元土体i的弹性恢复变形；
[0084]
单元土体i的水平向附加应力由σ
h0
衰减至σ
ht
时，土体的弹性恢复应变为：
[0085][0086]
式中：表示t时刻路基土的弹性恢复应变。
[0087]
故单元土体i在t时刻的实际蠕变为：
[0088][0089]
根据式(2)，σ
h0
和σ
ht
可分别表示为：
[0090]
σ
h0
＝q0khꢀꢀꢀ
(23)
[0091]
σ
ht
＝q
t
khꢀꢀꢀ
(24)
[0092]
式中：q0和q
t
分别表示板-土接触面处的初始水平均布荷载和t时刻水平均布荷载。
[0093]
考虑附加应力沿板-土接触面中心点后方水平路径的扩散规律，沿水平路径h积分可得半幅路基中板-土接触面中心点后方路基土的水平向蠕变变形l
st
为：
[0094][0095]
步骤二、建立钢筋回缩变形方程；
[0096]
预应力钢筋为典型的弹性材料，可采用虎克体(h体)模拟，其变形满足弹性定律。设t时刻钢筋张拉力为f
pt
，则半幅路基模型下钢筋沿其轴向的回缩应变ε
pt
(压缩为正，拉伸为负)和回缩变形l
pt
可分别由下式表示。
[0097][0098][0099]
式中：f
p0
为钢筋的初始张拉力，as为钢筋截面面积，es为钢筋的弹性模量，h为路基两侧侧压板与路基接触面中心点的水平距离，h为侧压板与路基接触面中心点后方水平路径上土体单元i距路基坡面的水平距离。
[0100]
步骤三、将钢筋、侧压板与路基接触面中心点后方土体视为多个相互独立的元件模型，通过侧压板与路基接触面的位移相容性与应力连续性建立联系，构建钢筋张拉力与路基土蠕变的耦合效应模型(如图8所示)
[0101]
根据式(1)，路基板-土接触面处的初始水平均布荷载q0和t时刻水平均布荷载q
t
可分别表示为：
[0102][0103][0104]
若不考虑锚具和侧压力板等的变形，则任意t时刻钢筋的回缩变形l
pt
与路基土的蠕变变形l
st
应满足如下表达式：
[0105]
l
st
＝l
pt
ꢀꢀꢀ
(30)
[0106]
将式(25)、(27)、式(28)、式(29)代入式(30)，则钢筋张拉力f
pt
可表达为式(30)。
[0107]
得到t时刻钢筋张拉力f
pt
的预测方程：
[0108][0109]
其中：f
p0
为钢筋的初始张拉力，h为路基两侧侧压板与路基接触面中心点的水平距离，b和l分别为侧压板底面沿线路纵向和路基坡面方向的长度，as为钢筋截面面积，es为钢筋的弹性模量，kh为板-土接触面中心点后方水平路径上任一点处的水平附加应力系数，em、ek分别为maxwell体、kelvin体的弹性常数，ηm、ηk分别为maxwell体、kelvin体的黏性常数，h为侧压板与路基接触面中心点后方水平路径上土体单元i距路基坡面的水平距离。
[0110]
基于flac 3d仿真平台建立典型预应力路基的有限差分数值模型，并利用有限差分数值模型对三种不同工况下钢筋张拉力的损失情况进行模拟，通过将模拟结果与本发明分析方法得到的结果进行对比，结果表明：钢筋张拉力随时间损失的预测曲线与数值仿真曲线均吻合良好，二者偏差不足5％，论证了本文提出的路基预应力损失模型的有效性。
[0111]
本技术基于预应力钢筋回缩变形与路基土蠕变变形的相容性、路基两侧侧压力板与路基土接触面处的应力连续性及路基内附加应力的扩散效应，提出预应力路基的预应力损失模型。以burgers蠕变模型描述路基土的蠕变行为为例，推导了具体的路基预应力损失方程，并基于flac 3d数值仿真验证模型的有效性。本文方法考虑了附加应力在预应力路基内的扩散效应，计算原理清晰，对土体蠕变处理简便，得到的预测方程能够准确预测土体蠕变引起的预应力钢筋张拉力损失，进而能够指导后续预应力的补张拉，对保障锚固工程的长期安全具有重大意义。
[0112]
上述本发明所公开的任一技术方案除另有声明外，如果其公开了数值范围，那么公开的数值范围均为优选的数值范围，任何本领域的技术人员应该理解：优选的数值范围仅仅是诸多可实施的数值中技术效果比较明显或具有代表性的数值。由于数值较多，无法穷举，所以本发明才公开部分数值以举例说明本发明的技术方案，并且，上述列举的数值不应构成对本发明创造保护范围的限制。
[0113]
同时，上述本发明如果公开或涉及了互相固定连接的零部件或结构件，那么，除另有声明外，固定连接可以理解为：能够拆卸地固定连接(例如使用螺栓或螺钉连接)，也可以理解为：不可拆卸的固定连接(例如铆接、焊接)，当然，互相固定连接也可以为一体式结构(例如使用铸造工艺一体成形制造出来)所取代(明显无法采用一体成形工艺除外)。
[0114]
另外，上述本发明公开的任一技术方案中所应用的用于表示位置关系或形状的术语除另有声明外其含义包括与其近似、类似或接近的状态或形状。本发明提供的任一部件既可以是由多个单独的组成部分组装而成，也可以为一体成形工艺制造出来的单独部件。
[0115]
上述实施例仅仅是清楚地说明本发明所作的举例，而非对实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里也无需也无法对所有的实施例予以穷举。而由此所引申出的显而易见的变化或变动仍处于本发明的保护范围之中。