一种小子样条件下基于模糊理论的参数不确定性建模方法

1.本发明属于不确定性建模与数据分析领域，具体涉及一种小子样条件下基于模糊理论的参数不确定性建模方法。


背景技术：

2.由于现代装备产品结构复杂、成本高昂且失效机理复杂，基于试验方法与统计概念的传统可靠性分析技术已逐渐被可靠性仿真分析技术替代。可靠性仿真分析技术主要涉及数字样机、协同仿真及可靠性工程等技术领域，可为产品的综合设计、评估分析及综合优化等工作提供研究途径和数据支持。
3.装备产品的可靠性仿真通常依靠材料、物理、力学、电学、统计、可靠性等多学科的交叉融合来实现，其中涉及到大量的材料性能、结构装配尺寸、环境与工况载荷等模型参数。受自然缺陷随机分布、人类客观技术水平和主观认知因素的影响，上述参数往往表现出较为明显的扰动和不确定性特征。在可靠性仿真过程中，这些模型参数的不确定性会沿着装备产品的层次结构逐级传播，最终影响到产品功能输出、使用寿命及可靠性水平。但在工程实际中由于受时间成本、经济成本、技术水平及人为因素的制约，可获取的样本信息有限其常以小子样样本的形式存在，以至于不能充分、完整地反映出模型参数的分散性特点。模型参数不确定性表征结果对产品可靠性仿真评估结果的精度水平产生重大影响，通过模糊理论得到符合参数特征的取样值具有很高的工程实用价值。
4.在样本量相对较小时，由于受到抽样随机性的影响，传统的概率不确定性建模方法会存在很大的误差，而模糊理论可以通过引入人的主观认知，采用隶属度函数来量化参数取值隶属于不同取值的程度和可能性，一定程度上提高参数的不确定性量化精度。


技术实现要素：

5.为克服在小子样条件下现有技术不能有效反映模型参数不确定性特点的问题，本发明提出一种小子样条件下基于模糊理论的参数不确定性建模方法。
6.本发明技术方案：一种小子样条件下基于模糊理论的参数不确定性建模方法构建过程如下：
7.步骤1：确定样本的上下限，根据样本个数确定样本分组数，并建立相应的子区间，求得每个子区间的区间中值和隶属度；
8.步骤2：对样本数据进行三角概率分布、正态概率分布的分布拟合，后基于信息熵等价转换法求解三角型、正态型隶属度函数的特征值；并基于得到的特征值为模型参数建立相应的隶属度函数；
9.步骤3：若已知参数隶属度函数类型的先验信息，则直接采用相应类型的隶属度函数。若无先验信息，则分别计算步骤1所得隶属度相较于步骤2所建立的各种隶属度函数的残差平方和，取残差和最小的隶属度函数为参数的最优隶属度函数；
10.步骤4：使用接受-拒绝采样方法，基于最优隶属度函数开展随机采样，生成参数的
随机采样数据。
11.其中，步骤1首先将样本区间等分成k组，由一定的工程经验及主观设定样本数量为x时的组数n如公式(1)所示：
[0012][0013]
同时，把落入各个区间中的样本个数ni与样本数最多区间的样本个数n
max
的比值作为该区间的隶属度μi，即得到了样本区间及区间隶属度。
[0014]
为构建参数的隶属度函数，步骤2中首先进行概率分布的拟合，后基于熵等价转换法h
x
＝gy(h
x
为随机变量概率熵，gy为模糊变量模糊熵)求解相应隶属度函数的特征值，进而构建了相应类型的隶属度函数。此处以三角型隶属度函数为例说明隶属度函数的构建过程：
[0015]
首先，三角分布的概率密度函数如式(2)所示：
[0016][0017]
其次，由矩估计法计算三角分布的原点矩如式(3)所示：
[0018][0019]
由式(2)及式(3)的一阶矩得其中为样本均值，a为样本区间最小值，b为样本区间最大值,c为三角分布中概率密度最大处的值。
[0020]
最后，基于信息熵等价转换法求解隶属度函数的特征值：
[0021]
概率熵、模糊熵的计算公式如式(4)和式(5)所示：
[0022]hx
＝-∫
x
f(x)lnf(x)dx
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0023]gy
＝-∫yμ
′
(y)lnμ
′
(y)dy
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0024]
其中，f(x)为随机变量的概率密度函数，μ
′
(y)为模糊变量的隶属度函数μ(x)归一化后的函数h
x
为随机变量概率熵，gy为模糊变量模糊熵。
[0025]
令概率熵与模糊熵相等如式(6)所示：
[0026]hx
＝gyꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0027]
基于式(6)可得到三角型隶属度函数隶属度为1时对应的参数取值为c，即为
[0028]
同理，基于上述步骤可求得正态型隶属度函数的特征值。
[0029]
故基于隶属度函数的特征值所构建的三角型隶属度函数为:
[0030][0031]
步骤3首先判断样本是否有隶属度函数类型的先验信息，如若已知隶属度函数类型，则直接采用相应类型的隶属度函数。若无先验信息，则分别计算步骤1所得隶属度相较于步骤2所建立的各个隶属度函数的残差平方和，取残差和最小的隶属度函数类型为样本所属的隶属度函数类型，从而建立了参数的隶属度函数；
[0032]
设f为m个点的离散函数，其离散实验观察数据为(xi,f(xi))。
[0033]
对于任意拟合函数s(x),残差的计算公式为：
[0034]
δi＝f(xi)-s(xi),i＝1,2,
…
,m
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0035]
残差平方和的计算公式为：
[0036][0037]
其中，ρ(xi)(i＝1,2,
…
,m)为权函数，表示该离散点的重要程度。
[0038]
通过求步骤1中分组得到的样本区间中值及隶属度与步骤2中得到各个隶属度函数求残差和，以此作为拟合优度评估指标，将所对应最小残差平方和的隶属度类型作为最优概率分布类型。
[0039]
步骤4中基于模糊隶属度函数，开展基于接受-拒绝方法的随机采样。
[0040]
第一步：从建议分布g中进行采样，获取一个采样样本y；
[0041]
第二步：从[0,1]的均匀分布中进行采样，获取一个采样样本u；
[0042]
第三步：判断，如果则接受这个采样值，如果不满足，则拒绝这个采样值，重新采样。重复这个步骤直至获得目标数量的采样值。
[0043]
通过上述步骤，可以完成在小子样条件下基于模糊理论的参数不确定性建模和参数的取样，用于小子样条件下参数的随机生成。
[0044]
据大数定理可知，在小样本的条件下采用概率不确定性建模方法建立观测样本的概率不确定性表征模型不能有效反映参数的分散性特征。本发明的方法基于模糊理论，可以从隶属度函数角度对取样参数进行建模和随机数生成，并能利用样本已有的隶属度函数类型，及样本上下限等主观信息，得到在一定程度上符合模糊理论的取样值，具有相应的优势。
[0045]
与现有技术相比，本发明的优点在于：本发明通过模糊理论的方法，通过构建隶属度函数来对小子样条件下样本参数进行了不确定性建模，实现了小子样条件下基于模糊理
论的参数随机生成。相较于传统的概率理论，本方法引入了模糊理论中的隶属度，还能利用样本已有的隶属度函数类型，及样本上下限等主观信息，使得参数在小子样条件下建立了更有效的不确定性表征模型。
附图说明
[0046]
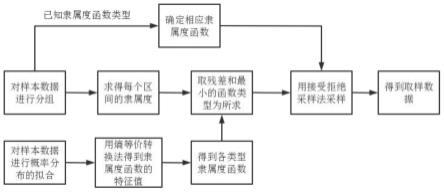
图1本发明提供的方法流程图；
[0047]
图2样本区间中值及隶属度点图；
[0048]
图3正态型隶属度函数及隶属度点图；
[0049]
图4三角型隶属度函数及隶属度点图；
[0050]
图5梯型隶属度函数及隶属度点图；
[0051]
图6抽样数据的直方图。
具体实施方式
[0052]
下面结合实施例和附图对本发明做更进一步的说明。
[0053]
图1为小子样条件下基于模糊理论的参数不确定性建模方法的流程图，此处基于图1所示的方法流程开展案例应用研究。
[0054]
选取[10.2,13.5,11.6,12.4,11.2,9.8,11.5]七个数据作为输入值。
[0055]
步骤1：确定样本的上下限，根据样本个数确定样本分组数，并建立相应的子区间，求得每个分组的区间中值和隶属度；
[0056]
由于输入数据为7个，由公式(1)可得，样本分组数n为3，采样数据最小值和最大值分别为9.8和13.5。据工程经验可知参数取值的上限应比样本最大值略大，参数取值的下限应比样本最小值略小，若存在已知信息则可直接采用，不存在已知信息时由工程经验分别取样本上下限为14.03和9.27。因此，所分成的3个样本区间分别为[9.27,10.95]，[10.95,12.63]，[12.63,14.03]。落入上述这三个区间的样本个数分别为2个，4个和1个，即n
max
为4，则三个区间隶属度分别为0.5、1和0.25，得到(区间中值xi,xi处的隶属度μi)数组为(10.11，0.5)，(11.79，1)，(13.33，0.25)，数组点图如图2所示。
[0057]
步骤2：对样本数据进行三角概率分布、正态概率分布的分布拟合，后基于信息熵等价转换法求解三角型、正态型隶属度函数的特征值；并基于得到的特征值为模型参数建立相应的隶属度函数；
[0058]
通过公式(4)、(5)、(6)得到三角型隶属度函数的c值为11.11，得到正态型隶属度函数的位置参数和形状参数分别为11.47和1.17，基于样本得到梯型隶属度函数的分段点为10.125和11.525。
[0059]
由公式(7)可得三角型隶属度函数为式(10)，正态型隶属度函数和梯型隶属度函数为式(11)和式(12)。
[0060][0061][0062][0063]
步骤3：若样本已知隶属度函数类型的先验信息，则直接采用相应类型的隶属度函数。若无先验信息，则分别计算步骤1所得隶属度相较于步骤2所建立的各种隶属度函数的残差平方和，取残差和最小的隶属度函数为参数的最优隶属度函数；
[0064]
步骤1所得数组与各个类型隶属度函数示意图如图3、图4、图5所示。
[0065]
由式(9)计算可得在不同隶属度函数下的残差平方和如表1所示。
[0066]
表1各类型隶属度残差平方和计算
[0067]
隶属度函数类型正态型三角型梯型残差平方和||δ||20.04220.004030.216
[0068]
根据表1中的残差平方和数据，此处选择正态型隶属度函数作为样本参数的隶属度函数，即所建立的参数的隶属度函数如式(11)所示。
[0069]
步骤4：使用接受-拒绝采样方法，基于最优隶属度函数开展随机采样，生成参数的随机采样数据。
[0070]
采用g(x)＝1作为建议分布，对函数进行接受拒绝法采样，重复n次，即得到抽样数据，抽样数据的直方图如图6所示。
[0071]
以上所述，仅为本发明部分具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本领域的人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。